(2.2) 5_Qlassical_oscillator (2)

1.

Сведения из теории вероятности
Вероятность i-го события для дискретной случайной величины
Ni
wi
N N
N i - число благоприятных событий, N - полное число событий
Среднее случайной дискретной величины f i
fN f N
f 1 1 2 2
N
fn Nn
N
f k wk
k 1
Дисперсия случайной дискретной величины
f f f f f f f f w f w f
2
2
2
2
k 1
2
k
2
k
k 1
2
k
k
2

2.

Плотность распределения вероятности случайной непрерывной величины
( )
Вероятность обнаружить случайную величину в интервале ,
w ,
d ( )
Среднее случайной непрерывной величины
d ( )
Дисперсия случайной непрерывной величины
2
2
2 2 d ( )
2
Физический смысл среднего значения и дисперсии. Обсудить, когда достаточно знать
только среднее значение.
Найти среднее значение и дисперсию координаты для классического осциллятора?

3.

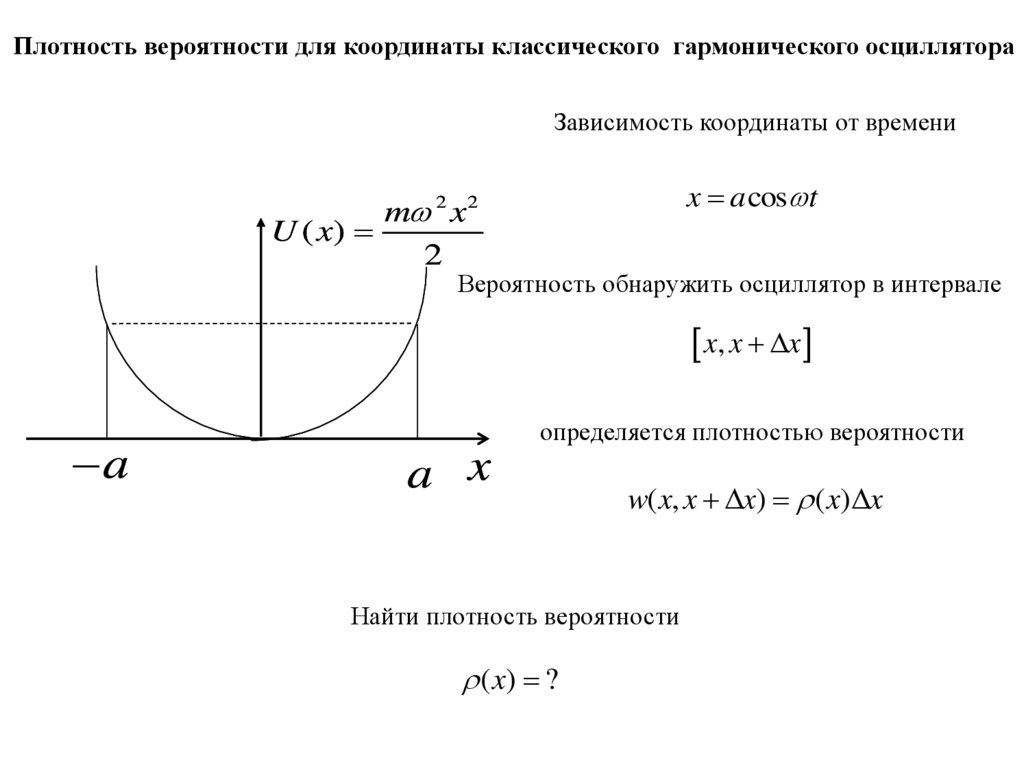
Плотность вероятности для координаты классического гармонического осциллятора
Зависимость координаты от времени
x a cos t
m 2 x 2
U ( x)
2
Вероятность обнаружить осциллятор в интервале
x, x x
a
определяется плотностью вероятности
a x
w( x, x x) ( x) x
Найти плотность вероятности
( x) ?

4.

Вероятность «ткнуть пальцем» и попасть в частицу в интервале x
пропорциональна времени нахождения частицы в нём
( x) dx Adt ( x)
x
a
a x
Найти плотность вероятности
( x) ?

5.

Промежуточные формулы
t ( x)
1
arccos
x
a
1
1
dt
a 1 ( x / a) 2
( x)
A
1
a 1 ( x / a) 2
Из какого условия можно найти A?

6.

Условие нормировки
a
a
A
dx
(
x
)
dx
a
a a
1
1 ( x / a) 2
2A
1
d
0
1
1 2
A
1
Плотность вероятности
( x)
1
a2 x2
Найти среднее значение и дисперсию координаты для классического осциллятора?

7.

Среднее значение координаты для классического осциллятора
a
x dx x ( x)
a
1
a
dx
a
x
a x
2
2
0
Дисперсия координаты для классического осциллятора
a
x x dx x ( x)
2
2
a
1
a
dx
a
1
a2 x2
dx
dx
2
2
2
2
a
a x
a x
a
x2
a
a
2
2
a x
a2

8.

Дисперсия координаты для классического осциллятора
a2
x x
2
2
Найти вероятность обнаружить осциллятор вблизи
точки остановки
a a, a , a
w(a a, a) ?
a
ax
a

9.

Промежуточные формулы
a
w(a a, a) dx ( x)
a a
1
a
dx
a a
1
a2 x2
arcsin x arcsin y arcsin x 1 y 2 y 1 x 2

10.

Вероятность обнаружить осциллятор вблизи точки остановки
2
a 1 2 a
w(a a, a) arcsin 1 1
a
a
1

11.

Задачи на дом
1. Найти плотность распределения вероятности, среднее значение и дисперсию координаты
классической частицы в прямоугольной яме шириной a. Энергия частицы E.
2. Плотность распределения вероятности квантового осциллятора
x2
( x) A exp 2
2a
Найти среднее значение и дисперсию координаты квантового осциллятора.

12.

Ответы
1 задача
1
a
( x) , x ,
a
2
a2
x x
12
2
2 задача
a2
x 0, x x
2
2