Similar presentations:
Вычислительные основы линейной алгебры. Итерационные методы решения систем уравнений
1.
ОП.11 ЧИСЛЕННЫЕ МЕТОДЫ В ПРОГРАММИРОВАНИИТема 1.4 Вычислительные
основы линейной алгебры
Итерационные методы решения систем
уравнений.
Метод простых итераций.
Метод Зейделя.
Метод релаксаций.
Ковалева Елена Вячеславовна e.kovaleva@mgutm.ru
2.
Собственный вектор и собственныечисла матрицы
ОПРЕДЕЛЕНИЕ. Ненулевой вектор
называется
собственным вектором матрицы A , если найдётся такое
число λ , что
λ называется собственным (характеристическим)
числом матрицы A .
3.
Нахождение собственных значенийХарактеристическое уравнение матрицы A:
4.
Норма элемента5.
Свойства норм6.
Примеры нормированных пространств7.
Норма матрицы8.
Метод простой итерациидля решения систем линейных уравнений
Имеем линейную систему уравнений с n
неизвестными:
a11x1 a12 x2
a1n xn b1 ,
a21 x1 a22 x2 a2 n xn b2 ,
…
an1 x1 an 2 x2 ann xn bn .
(2.1)
9.
Эквивалентная система уравнений:x1 f1 c12 x2 c13 x3 ... c1n xn ,
x2 f 2 c22 x2 c23 x3 ... c2 n xn ,
…
(2.2)
xn fn cn 2 x2 cn3 x3 ... cn,n 1xn 1 ,
bi c aij
где fi ; ij a
при i j и
ii
aii
cii 0 i, j 1,2,..., n
(2.3)
10.
Итерационный процесс для системы (2.2):x ( k 1) f cx ( k )
k 0,1,2,... ,
(2.4)
где k – номер итерации.
Для сходящегося процесса решением является
x lim f cx ( k ) .
k
(2.5)
11.
Условие сходимости:aii aij
i j
i, j 1,2,..., n ,
(2.6)
т.е. модуль диагонального коэффициента для каждого
уравнения больше суммы модулей его недиагональных
коэффициентов.
Теорема 1. Необходимым и достаточным условием
сходимости метода простых итераций при любом
начальном х к решению системы является требование
чтобы все собственные числа матрицы С были по
.
модулю меньше 1.
12.
Условие завершения итерационного процесса:xi( k ) xi( k 1)
(2.7)
Теорема 2. Если С q 1 , то при любом
начальном векторе x(0) метод простых итераций
сходится к единственному решению x* и при все
k N справедливы оценки погрешности
q
*
(k )
апостериорная
x x
x( k ) x( k 1)
q 1
k
q
x* x( k )
x(1) x(0)
априорная
q 1
13.
Замечания1. Априорная оценка, как правило, грубее
апостериорной.
2. Априорная оценка k-го приближения
3. Априорная оценка позволяет заранее
подсчитать число итераций, достаточное для
получения решения с заданной точностью
14.
ПримерДля системы записать какой-нибудь сходящийся
процесс метода простых итераций. За сколько шагов
этого процесса, можно достичь точности ε = 0,001 по
норме максимум? Найти третье приближение и оценить
его абсолютную погрешность и сравнить ее с истинной
погрешностью, зная точное решение системы
Х=(1;-2;1)
15.
16.
17.
Априорная оценка погрешности 3-го приближенияАпостериорная оценка погрешности
18.
2.5. Метод Зейделя для решения линейных системМетод Зейделя представляет собой некоторую
модификацию метода простой итерации.
Считаем, что дана линейная система, приведенная
к итерационному виду (2.2):
n
xi f i cij x j i 1, 2,..., n .
j 1
(2.8)
19.
Полагаем, что найдено k-е приближение xi( k )всех корней. Согласно методу Зейделя, (k+1)-е
приближение корней будет определяться по следующим
формулам:
n
x1( k 1) f1 cij x(jk ) ,
j 1
x2( k 1) f 2 c21 x1( k 1) c22 x2( k ) c23 x3( k ) ... c2 n xn( k ,)
( k 1)
3
x
( k 1)
31 1
f3 c x
( k 1)
32 2
c x
…
c x
(k )
33 3
... c x ,
(k )
3n n
(2.9)
i 1
n
j 1
j i
xi( k 1) fi cij x(jk 1) cij x(jk ),
( k 1)
n
x
n 1
f n cij x
j 1
( k 1)
j
…
c x , (k 0,1, 2,...) .
(k )
nn n
20.
Метод Зейделя обеспечивает, как правило, лучшуюсходимость, чем метод простой итерации.
21.
Пример22.
Задание для самостоятельного решенияДля системы записать какой-нибудь сходящийся процесс
метода простых итераций. За сколько шагов этого
процесса, можно достичь точности ε = 0,001 по норме
максимум? Найти третье приближение и оценить его
абсолютную погрешность. Выполнить 3 первые
итерации методом Зейделя.
23.
Информационное обеспечениеОсновные источники
1. Численные методы и программирование : учеб. пособие / В.Д.
Колдаев ; под ред. проф. Л.Г. Гагариной. — М. : ИД «ФОРУМ» :
ИНФРА-М, 2017. http://znanium.com/catalog/product/672965
Дополнительные источники
1. Введение в численные методы в задачах и упражнениях:
Учебное пособие / Гулин А.В.,Мажорова О.С.,Морозова
В.А.-М.:АРГАМАК-МЕДИА,НИЦ ИНФРА-М,2014
2. Численные методы (линейная алгебра и нелинейные
уравнения): учеб. пособие / В.М. Вержбицкий. – М.: Высш.
шк., 2017.














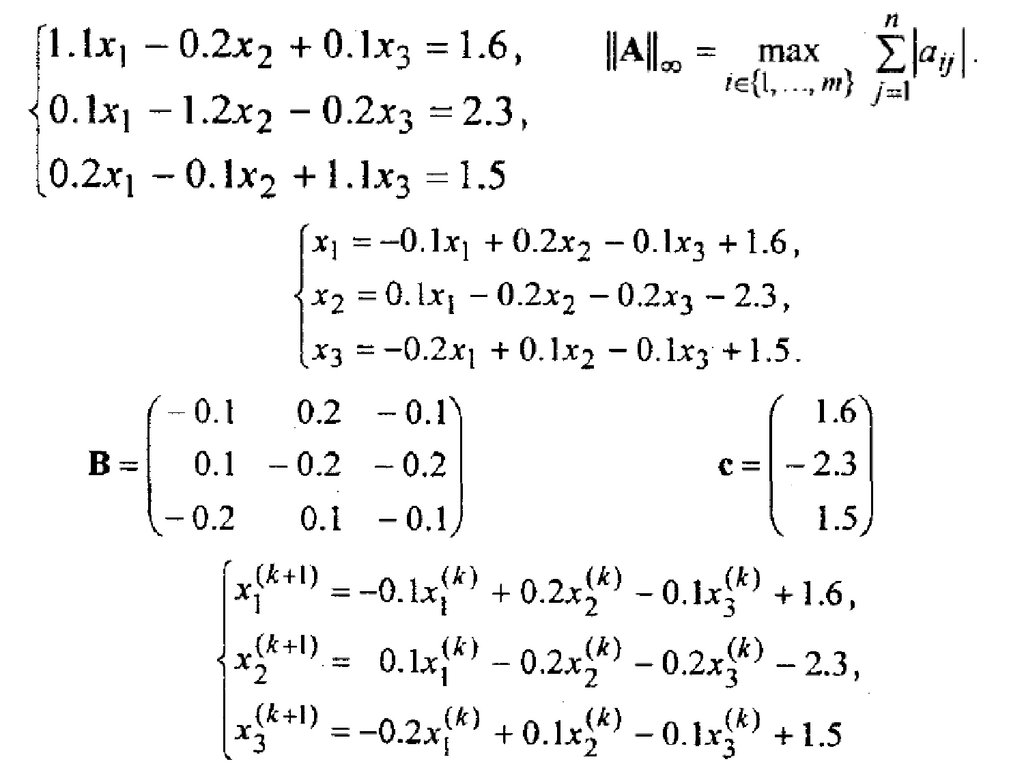








 mathematics
mathematics