Численные методы алгебры

1.

Численные методы алгебры

2.

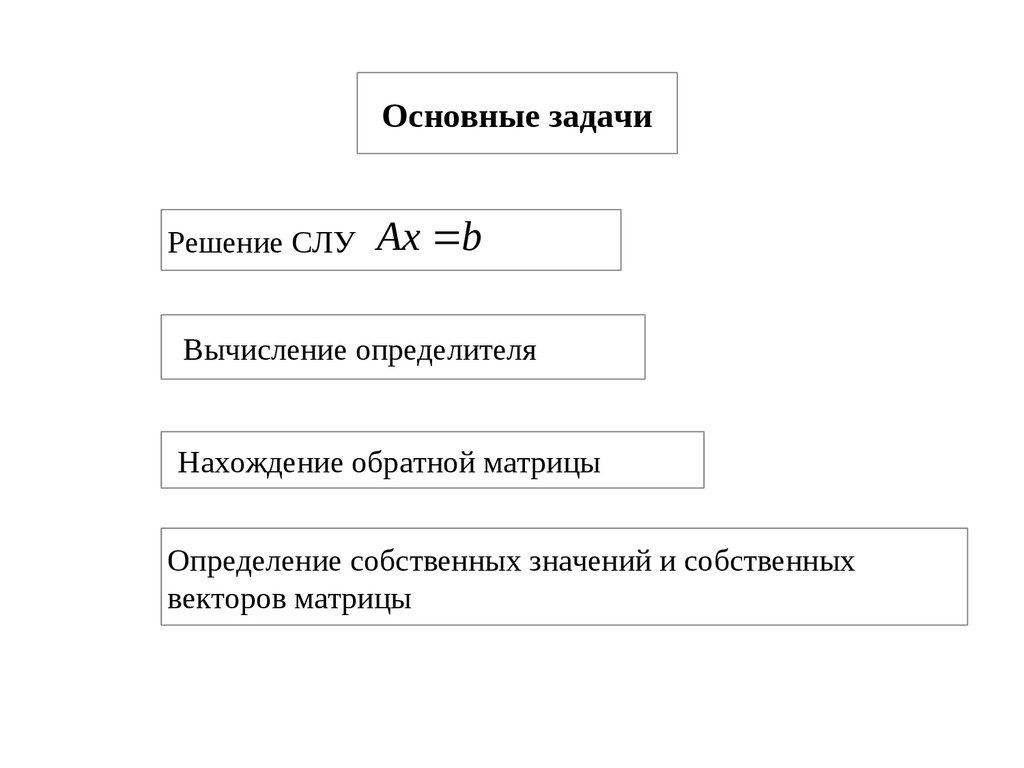
Основные задачи
Решение СЛУ
Ax b
Вычисление определителя
Нахождение обратной матрицы
Определение собственных значений и собственных
векторов матрицы
2

3.

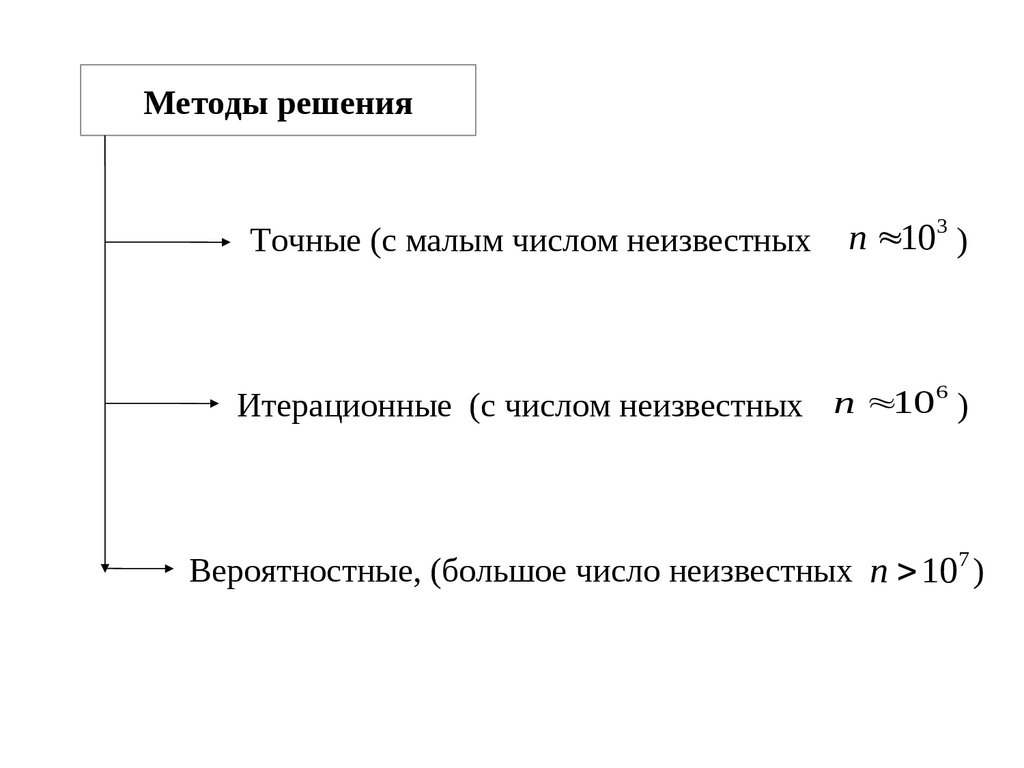
Методы решения
Точные (с малым числом неизвестных
n 103 )
6
n
10
Итерационные (с числом неизвестных
)
Вероятностные, (большое число неизвестных n 107 )
3

4.

Точные (с малым числом неизвестных n 103 )
Недостатки:
Требуют хранения в ОП сразу всей матрицы.
Не учитывают структуру матрицы (много
нулей).
Накапливание погрешностей в процессе
решения.
Число арифметических операций в методе Крамера
n ! n 1 n ! 1 n n ! n ! n ! 1 n n !
4

5.

Итерационные, (число неизвестных n 106 )
Норма вектора:
En
Пусть имеется n-мерное линейное пространство
n-мерных векторов
x x1 , x2 , , xn
Если для любого вектора
Такое число
x
x x
x Е n существует
такое, что
для x E
n
x y x y для x, y E n
x 0, если x 0.
Такое число
x называют нормой вектора x.
5

6.

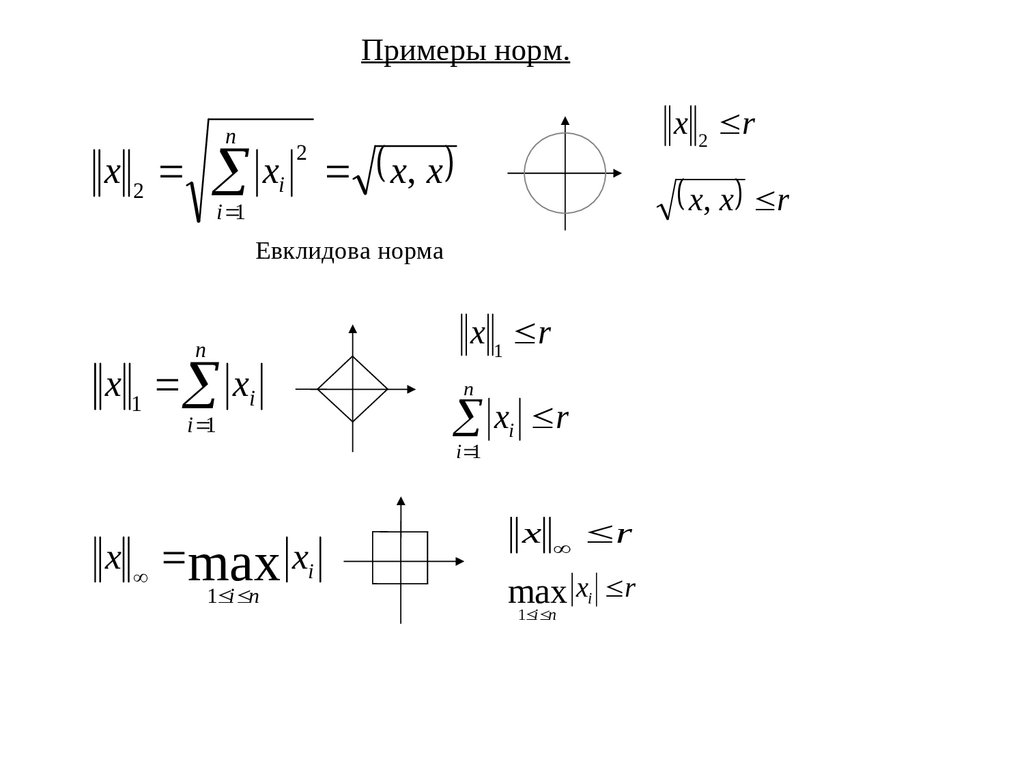
Примеры норм.
n
x2
x
2
i
x 2 r
x, x
x, x r
i 1
Евклидова норма
x 1 r
n
x 1 xi
i 1
n
xi
r
i 1
x
max xi
1 i n
x
r
xi
max
1 i n
r
6

7.

A2
i
max A* A
1 i n
n
A 1 max ai j
1 j n i 1
n
A max ai j
1 i n j 1
Норма матрицы, согласованная с
нормой вектора:
A sup
x 0
Ax
x
Геометрическая интерпретация нормы матрицы – максимальная
норма вектора, получаемого преобразованием A единичной сферы.
Или: радиус шара вектора образа изменяется в A раз.
A
7

8.

Итерационные методы (общие принципы)
С их помощью строится последовательность
x
k
такая, что
k
x
lim x,
k
где x – точное решение.
Эффективность итерационных методов определяется скоростью
сходимости последовательности приближений x k к решению.
Пусть ищется решение невырожденной системы уравнений
A x b
ШАГ 1. Преобразование исходной системы к виду C x B x d
Причём, системы эквивалентны, т.е. их решения
совпадают.
8

9.

ШАГ 2. Расстановка индексов (номеров приближений) в системе
C x B x d и задание нулевого приближения.
Например, C x k 1 B x k d , k 0, 1, 2,
где
x 0 x1 0 , x2 0 , , xn 0 заданный вектор.
k
ШАГ 3. Обоснование сходимости последовательных приближений x
полученных из C x k 1 B x k d к точному решению x и
оценка погрешности k-го приближения x k x
Оценка x k x позволяет при заданном ε остановить итерационный
процесс.
Различные итерационные методы отличаются шагами 1 и 2. Выбор
конкретного метода производится на основании оценки погрешности.
9

10.

Метод простой итерации. (МПИ)
ШАГ 1. Матрица C E , т.е. x B x b
A x b
Ex
Ex A x Ex b
Ex Ex A x b
Ex E A x b
B
x B x b
ШАГ 2. Составим рекуррентную формулу
x k 1 B x k b
10

11.

x1k 1 b11 x1k b12 x2k b1n xnk b1 ,
x2k 1 b21 x1k b22 x2k b2 n xnk b2 ,
xnk 1 bn1 x1k bn 2 x2k bnn xnk bn .
0
x
ШАГ 3. Выбираем начальное приближение
из каких-либо условий.
По рекуррентной формуле находим
k 1
k
x
x
Если метод сходится, тогда
x 1 , x 2 , , x k
уменьшается при
11
k

12.

Теорема 1 (достаточное условие сходимости МПИ).
Если
B 1 , то система
x B x b имеет
единственное решение и итерационный процесс по
формуле
x k 1 B x k b
сходится к точному
решению со скоростью убывающей геометрической
прогрессии
12

13.

Теорема 2 (необходимое и достаточное условие сходимости
МПИ).
Пусть система
x B x b
имеет единственное
решение и итерационный процесс по формуле
x k 1 B x k b
сходится к решению системы при
любом начальном приближении тогда и только тогда
когда все собственные числа матрицы B по модулю
меньше 1.
13

14.

Теорема 3
Пусть B q .1 Тогда при любом начальном векторе
x 0
МПИ сходится к единственному решению
системы
x B x b
и при k N справедливы
оценки погрешности:
q
x x k
x k x k 1
1 q
x x k
qk
x 1 x 0
1 q
На практике используют оценку:
апостериорная оценка
априорная оценка
x k x k 1
Это неравенство гарантирует сходимость МПИ только если q 1 2
14

15.

Замечание 1
Априорная оценка позволяет подсчитать заранее
число итераций k, достаточное для получения
искомого решения с заданной точностью ε, при
выбранном начальном векторе x 0
Замечание 2
Чем ближе x 0 к точному решению тем меньше
потребуется
итераций.
Если
нет
никакой
дополнительной информации о решении задачи,
тогда за x 0 обычно принимают вектор b свободных
членов системы
15

16.

Метод Зейделя
1. Решаем систему A x b
2. Важно – в матрице A все диагональные элементы
отличны от нуля.
a11 0 0
0 a12 a1n
B C x b
a21 a22 0 0
0 0 a23 a2 n
B
C
a a a
0 0 0 0
n1 n 2
nn
3. Построим рекуррентную формулу
B x k 1 C x k b
16

17.

a11 x1k 1 a12 x2k a1n xnk b1 ,
a21 x1 k 1 a22 x2 k 1 a23 x3 k a2 n xn k b2 ,
an1 x1 k 1 an 2 x2 k 1 an n 1 xn k 11 an n xn k 1 bn ,
1
a12 x2k a1n xnk b1 ,
a11
1
a21x1 k 1 a23 x3 k a2n xn k b2 ,
a22
x1k 1
x2 k 1
xn k 1
1
an1x1 k 1 an 2 x2 k 1 an n 1xn k 11 bn .
an n
17

18.

Если
Формула
x k x k 1 уменьшается, то метод сходится.
B x k 1 C x k b равносильна формуле
B x k 1 C x k b x k 1 B 1 C x k B 1 b
Итерационный процесс сходится если
B 1 C 1
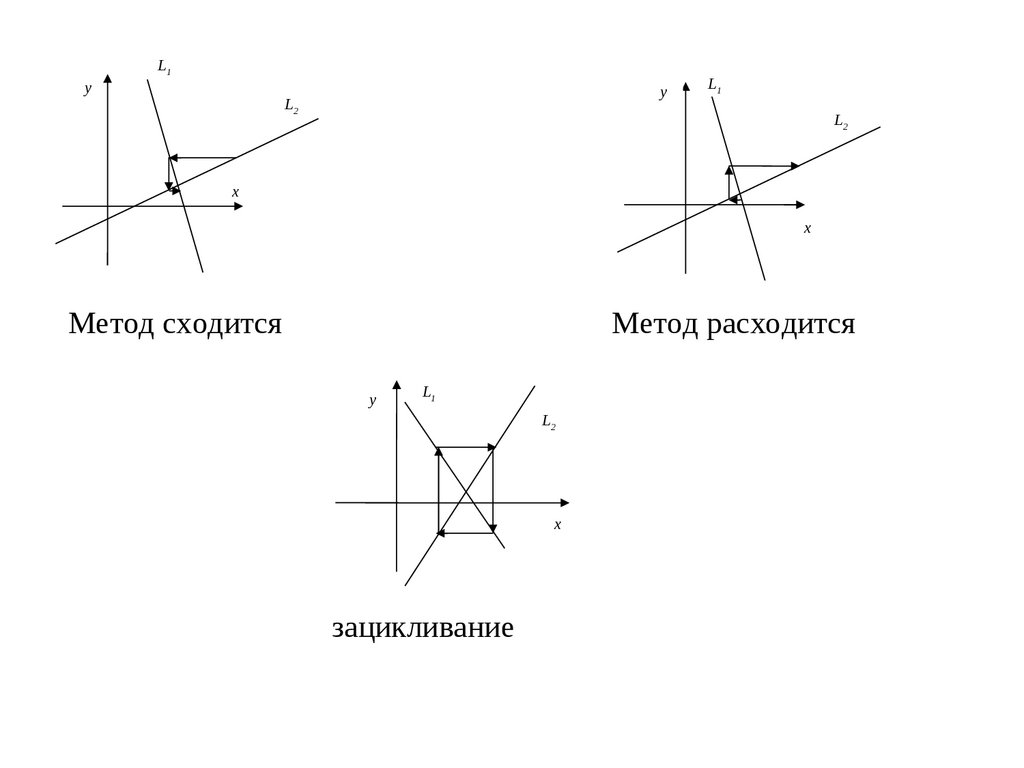
Геометрическая интерпретация метода
Каждое уравнение описывает плоскость
При получении приближения
из приближения
x
1
k 1
x
1
k 1
Li :
n
ai j x j bi 0
j 1
, , xi k 1 , xi k1 , , xn k
, , xi k1 1 , xi k , , xn k происходит
перемещение параллельно оси xi до пересечения с плоскостью Li
18

19.

L1
y
yy
L2
L1
L1
LL2
2
x
xx
Метод сходится
Метод расходится
yy
L
L1 1
LL2 2
xx
зацикливание
19

20.

Пример. Решить систему
2 x1 3x2 x3 1,
7 x1 2 x2 4 x3 6,
8 x1 x2 3 x3 12
методом простых итераций.
Решение.
3
1
1
x
0
x
x
x
,
1
2
3
1
2
2
2
7
x2 x1 0 x2 2 x3 3,
2
8
1
x3 3 x1 3 x2 0 x3 4
3
1
0
2
2
7
B
0 2
2
1
8
0
3
3
20

21.

1
7
8 1 11
3
B max ; 2 ; 1
2
2
3 3 2
2
3 1
1
7 8
37
B 1 max ; ; 2 1
2 3
2
6
2 3
Не выполняется достаточное условие сходимости (доминирование
диагональных элементов)
2 3 1 1
7 2 4 6
7 2 4 6
1 10 8 10
7 2 4 6 2 3 1 1 4 I
8 1 3 12
8 1 3 12 II I 2 I 1 2 8 44
2
4
6
9
x
0
x
x
x
,
B 1
1
2
3
1
7
7
7
10
48
1
8
B
1
x3 1,
x2 x1 0 x2
2
35
10
10
6 11 11
1
2
44
d max ; 1;
x3 8 x1 8 x2 0 x3 8
2 2
7
21

22.

x
0
d
x 0
6
7
1
11
2
4 11 6 14
1
6 2
x
0
1
2,
1
7 2 7 7
7 7
1 1 6
8 11
11
1 3 ,
x2 0 1
10 7
10 2
35
1 1 6 2
11 11
1
x3 1 0 5
8 7 8
2 2
7
1
Оценка погрешности найденных xi по формуле x x
22
k
B
d
1 B

23.

x 1 даёт значение корня с погрешностью
0.9 11 99
1
49,5
1 0.9 2
2
11 11 36
6
9
1 x 0 x 1 max 2 ; 1 3 ;
10
7
35
2
7
14
Следующий шаг итерации. Находим xi 2
и
2
0.9
2
11
1 0. 9 2
Точное решение:
11 15
5
;
;
2 2
23

24.

Методы вариационного типа
A x b
A
Где
вещественная положительно определённая (симметричная)
матрица, т.е.
A x, x 0
Построим квадратичный функционал
Ф x A x, x 2 b, x C
где С – const
Задача решения системы и задача минимизации функционала эквивалентны.
*
Нормальная система имеет единственное решение: обозначим его x
Тогда при любом векторе x x*
Ф x* A x* , x* 2 b, x* C
A x* , x* A x* , A , x* A , 2 b, x* 2 b, C
*
*
*
*
Ф
x
Ф x A x , A , x A , 2 b, Ф x A ,
b
A x* ,
*
24

25.

В силу самосопряжённости и положительности
A,
Ф x* minn Ф x
x R
Решение СЛАУ можно заменить задачей поиска минимума функции
многих переменных:
метод покоординатного спуска,
метод градиентного спуска,
метод минимальных невязок,
метод минимальных поправок,
метод минимальных итераций.
25

26.

Метод покоординатного спуска
y
x2
x10 x11
min2 Ф x1 , x20 const
x20 x12
min2 Ф x11 , x2
x R
(x
(x ,, yx02) )
0
10
x*x*
0
x R
x
x1
Метод градиентного спуска
x2
x k 1 x k k grad Ф x k
(x0 , x0 )
(x101, x202)
x2
Ф x k 1 Ф x k k grad Ф x k
x*
x*
Как выбирается параметр k ?
xx11
26

27.

Например выбирают из условия
min Ф x k k grad Ф x k
A x b, A x b
A A x b , A x b
k
k
метод наискорейшего спуска
k
k
k
Популярный метод сопряжённых градиентов
начало
x0 ,
Нач. вектор и уровень
допустимых погрешностей
Невязка нач. приближения
0 Ax 0 b
k=0
27

28.

, k
A k , k
k
k
x k 1 x k k k
k 1 k k k
k k 1
k 1
x k 1
конец
28