Similar presentations:
Векторы. Основные определения
1.
РАЗДЕЛ IIВЕКТОРНАЯ АЛГЕБРА.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ЛЕКЦИЯ 8
ВЕКТОРЫ
2.
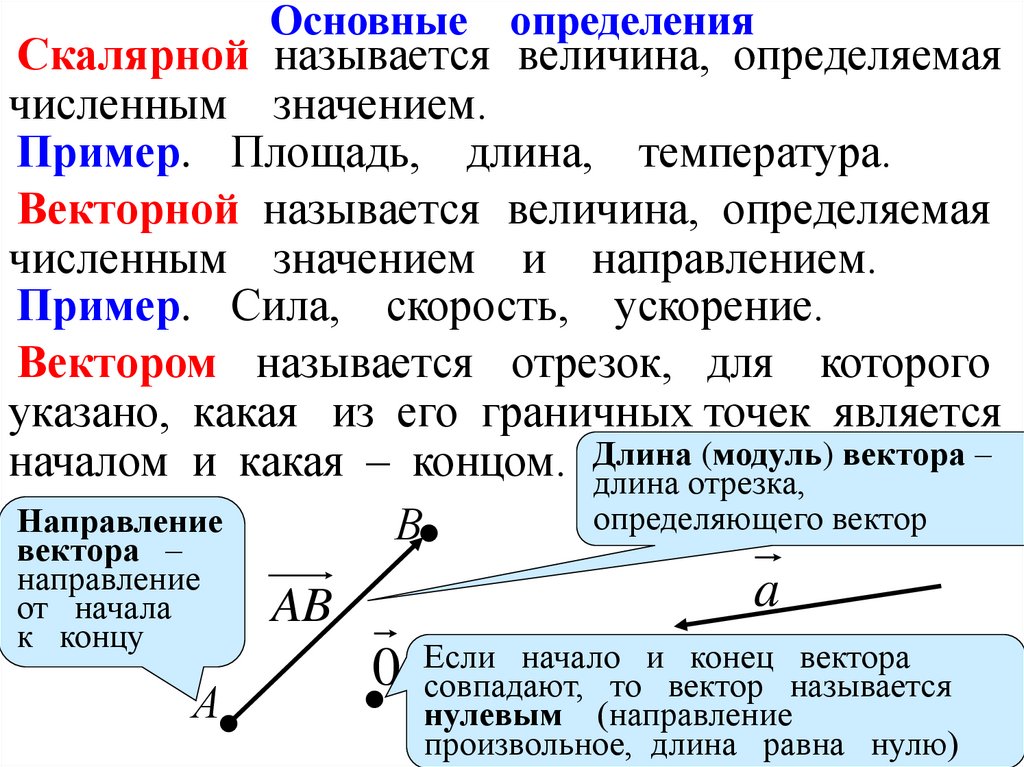
Основныеопределения
Скалярной называется величина, определяемая
численным значением.
Пример. Площадь, длина, температура.
Векторной называется величина, определяемая
численным значением и направлением.
Пример. Сила, скорость, ускорение.
Вектором называется отрезок, для которого
указано, какая из его граничных точек является
(модуль) вектора –
началом и какая – концом. Длина
длина отрезка,
определяющего вектор
Направление
В
вектора –
направление
от начала
к концу
А
AB
a
начало и конец вектора
0 Если
совпадают, то вектор называется
нулевым (направление
произвольное, длина равна нулю)
3.
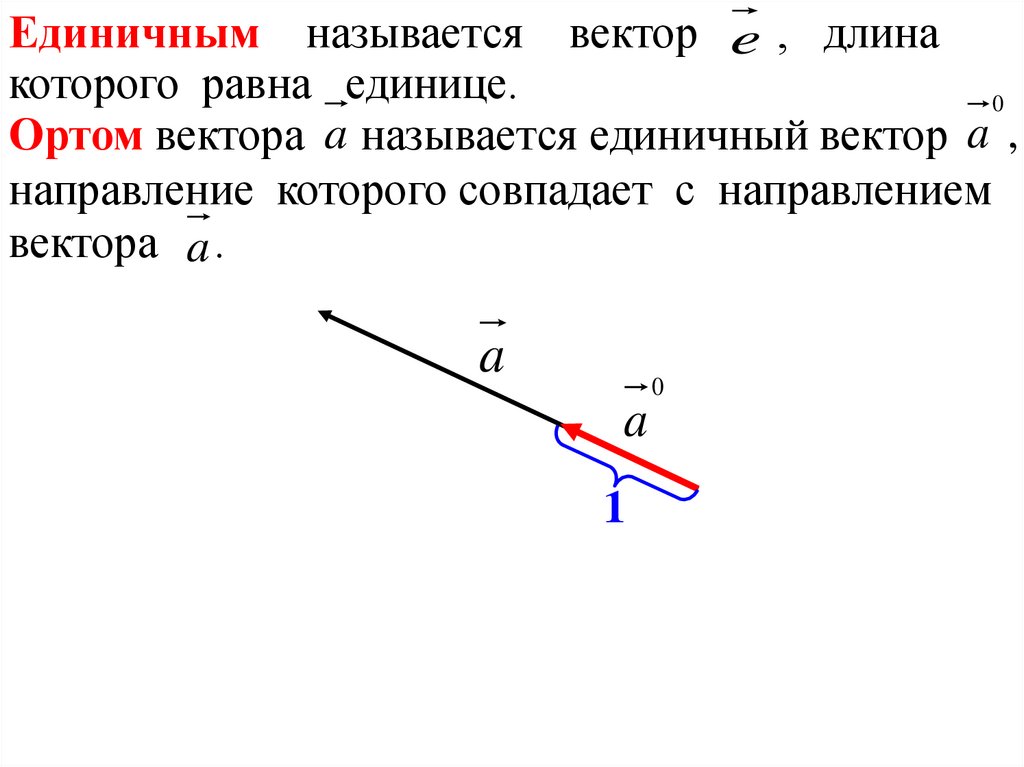
Единичным называется вектор e , длинакоторого равна единице.
0
Ортом вектора a называется единичный вектор a ,
направление которого совпадает с направлением
вектора a .
a
0
a
1
4.
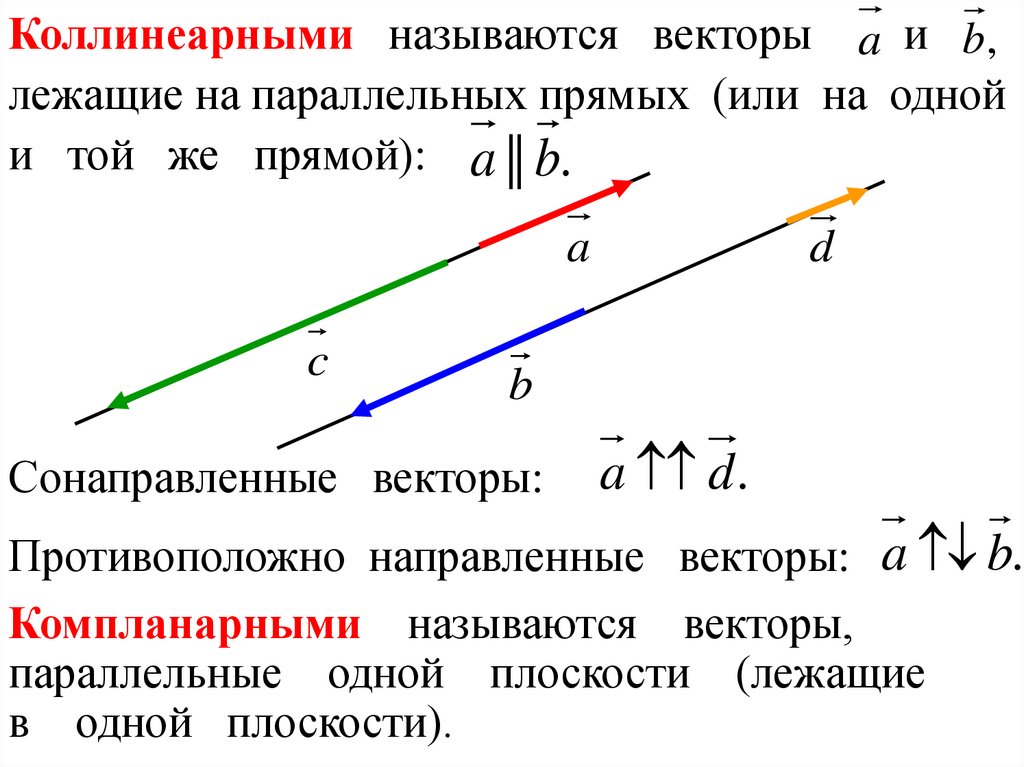
Коллинеарными называются векторы a и b ,лежащие на параллельных прямых (или на одной
и той же прямой): a || b.
a
c
d
b
Сонаправленные векторы:
a d .
Противоположно направленные векторы: a b.
Компланарными называются векторы,
параллельные одной плоскости (лежащие
в одной плоскости).
5.
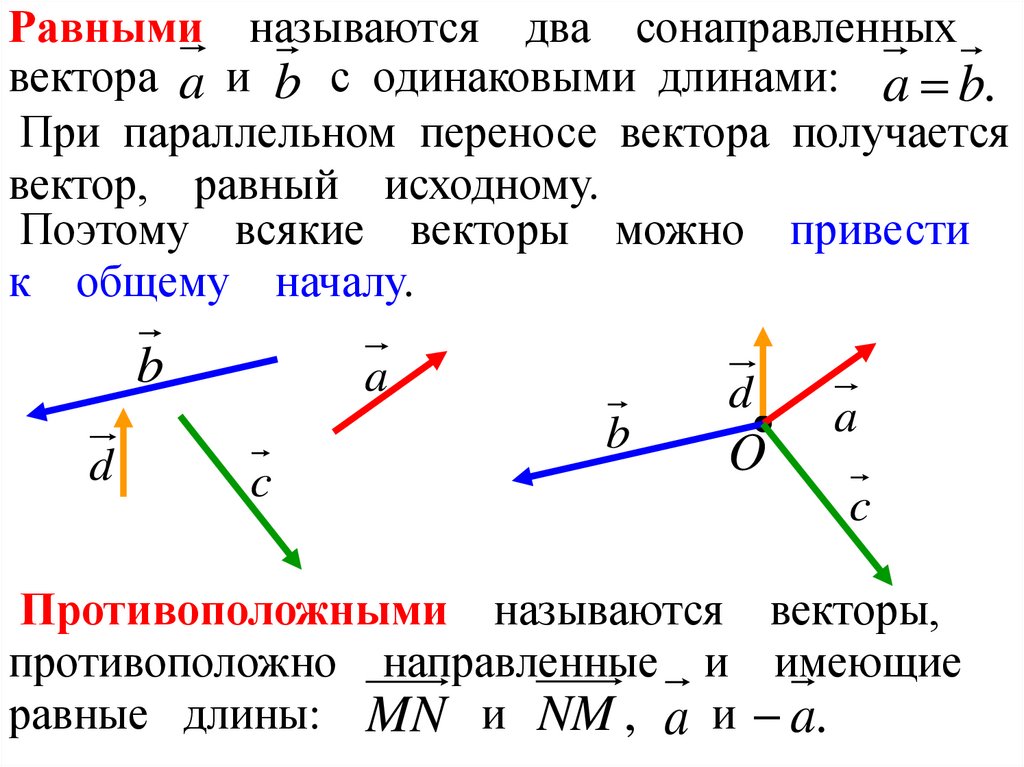
Равными называются два сонаправленныхвектора a и b с одинаковыми длинами: a b.
При параллельном переносе вектора получается
вектор, равный исходному.
Поэтому всякие векторы можно привести
к общему началу.
b
d
a
b
c
d
O
a
c
Противоположными называются векторы,
противоположно направленные и имеющие
равные длины: MN и NM , a и a.
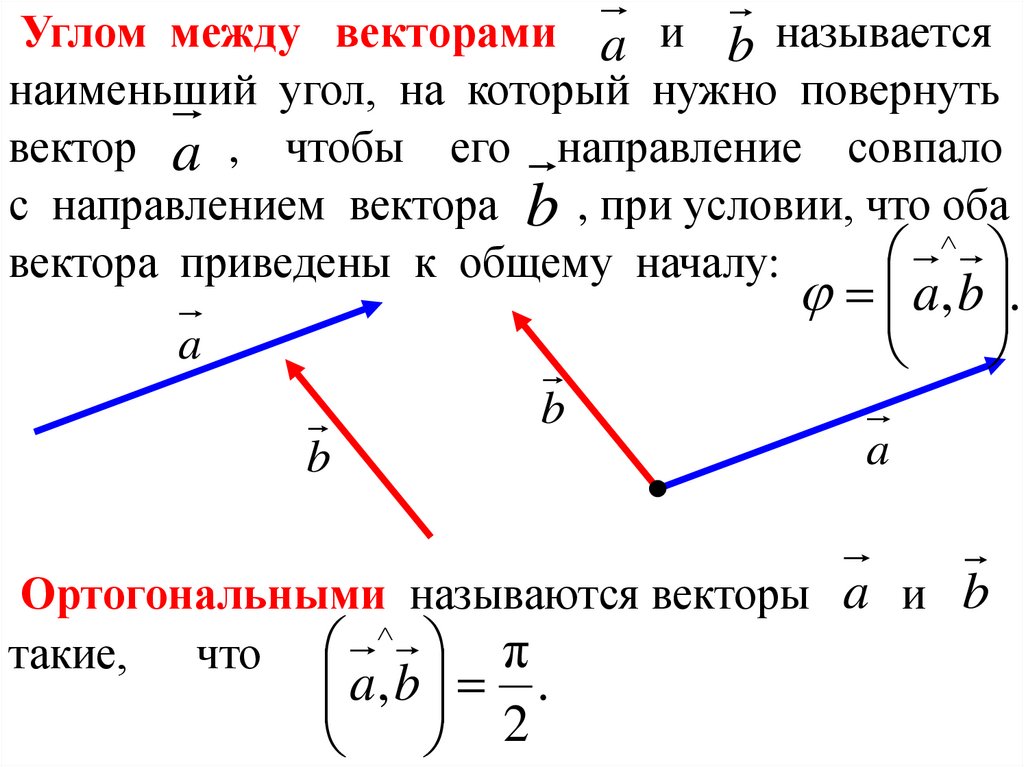
6.
Углом между векторами a и b называетсянаименьший угол, на который нужно повернуть
вектор a , чтобы его направление совпало
с направлением вектора b , при условии, что оба
вектора приведены к общему началу:
a, b .
a
b
b
a
Ортогональными называются векторы a и b
π
такие, что
a, b .
2
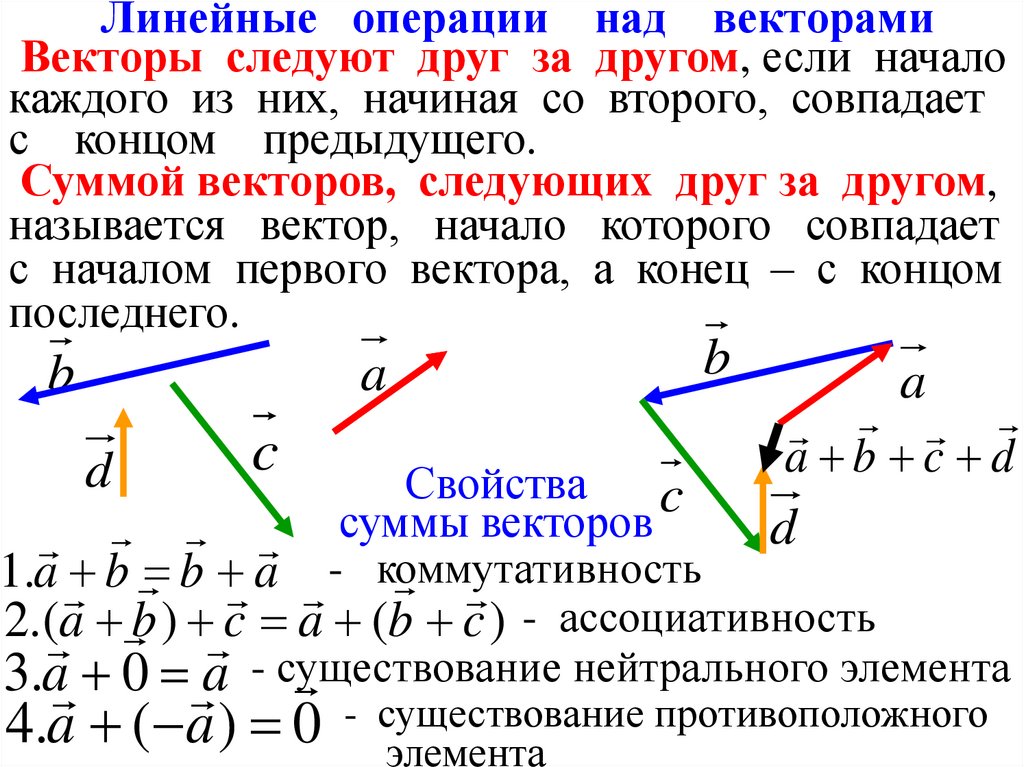
7.
Линейные операции над векторамиВекторы следуют друг за другом, если начало
каждого из них, начиная со второго, совпадает
с концом предыдущего.
Суммой векторов, следующих друг за другом,
называется вектор, начало которого совпадает
с началом первого вектора, а конец – с концом
последнего.
b
a
b
a
a b c d
c
d
Свойства
c
d
суммы векторов
1.a b b a - коммутативность
2.( a b ) c a (b c ) - ассоциативность
нейтрального элемента
3.a 0 a - существование
противоположного
4.a ( a ) 0 - существование
элемента
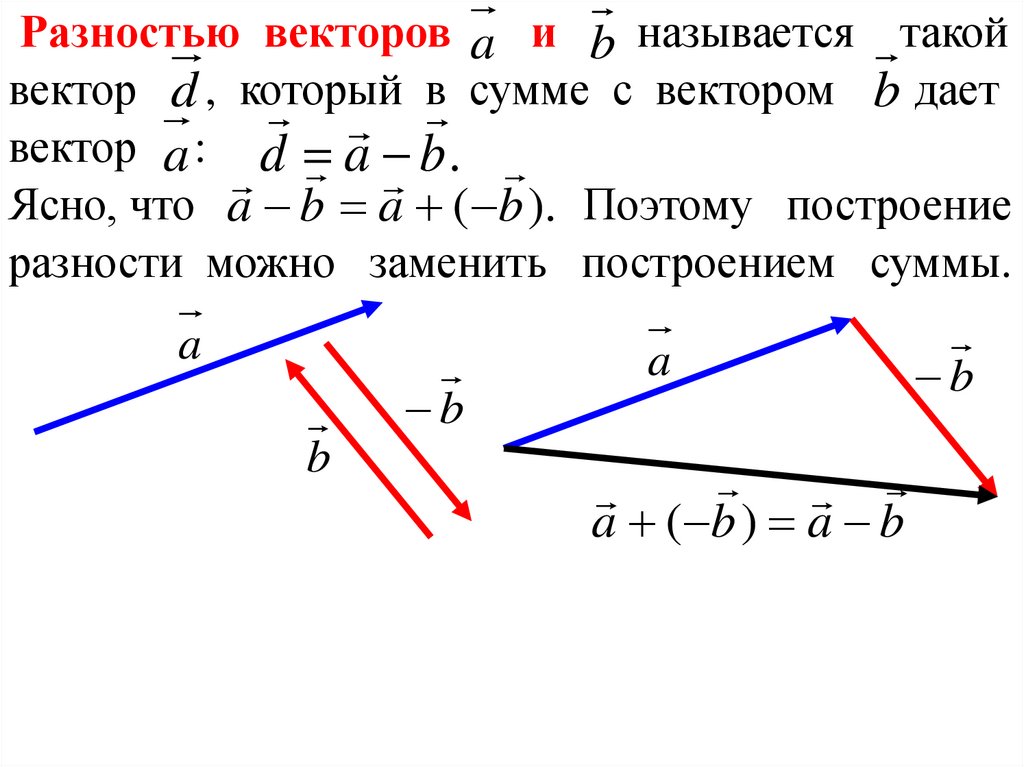
8.
Разностью векторов a и b называется такойвектор d , который
в сумме с вектором b дает
вектор a : d
a
b.
Ясно, что a b a ( b ). Поэтому построение
разности можно заменить построением суммы.
a
b
b
a
a ( b ) a b
b
9.
Произведением вектора a на действительноечисло λ называется вектор λa, длина которого
равна λ a , а направление совпадает
с направлением вектора a при λ 0,
и противоположно ему при λ 0.
Пример. По данным векторам a и b
1
построить вектор
b 2a.
1
b
2
a
2
b
1
b 2a
1
2a
2
|b|
2a
2a
2
a
1
b
2
10.
Теорема 8.1. Если ненулевые векторы a и bколлинеарны, то любой из них представим через
другой: b λa, λ 0 .
?
Доказательство. a || b
b λa.
Чтобы доказать равенство
векторов b и λ a
нужно показать, что b || λ a и
b | λa | .
a || b , a || λ a b || λ a b λa или b λa.
b
Если b λa, то b
a λa.
Длину вектора b можно
представить вот так:
Если
b λa,
a =λ
то
b
b
a
a λ a .
=λ
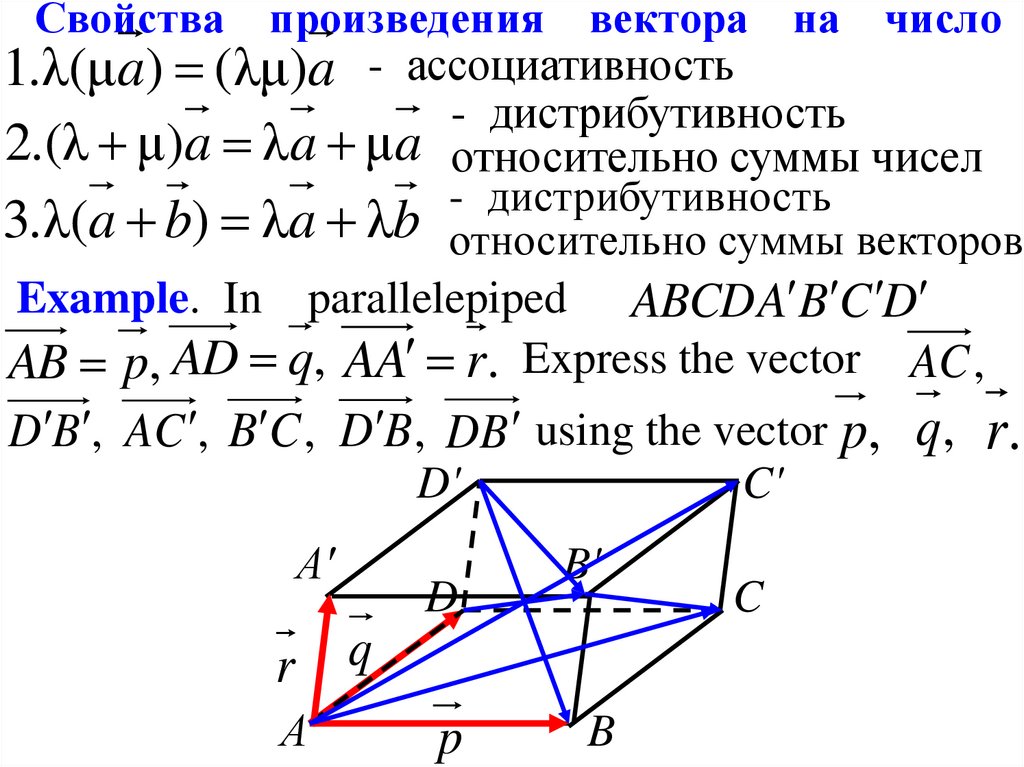
11.
Свойствапроизведения вектора на число
1.λ(μa) (λμ)a - ассоциативность
- дистрибутивность
2.(λ μ)a λa μ a относительно суммы чисел
- дистрибутивность
3.λ(a b) λa λb относительно суммы векторов
Example. In parallelepiped ABCD A B C D
AB p, AD q, AA r. Express the vector AC ,
D B , AC , B C , D B , DB using the vector p, q , r.
D'
А'
r
А
D
C'
B'
q
p
B
C



 mathematics
mathematics








