решение задач на цилиндр

1.

2.

Общая цилиндрическая поверхность,
её направляющая L и образующая m
L
m

3.

Наклонный круговой цилиндр
круг
Н

4.

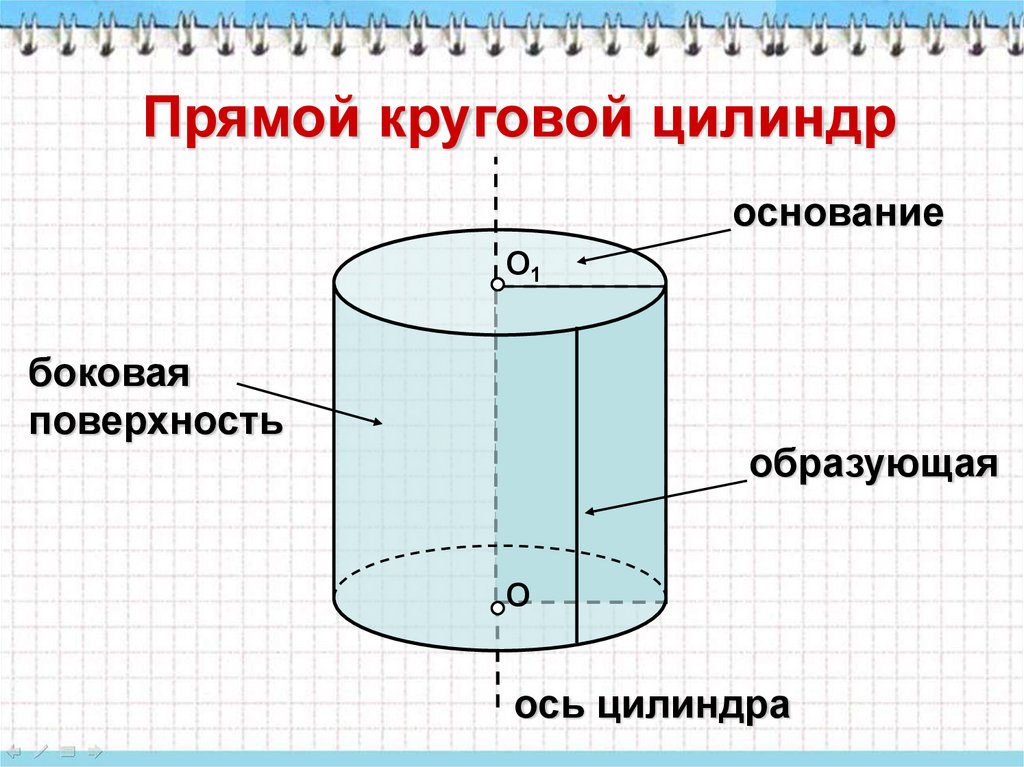
Прямой круговой цилиндр
основание
О1
боковая
поверхность
образующая
О
ось цилиндра

5.

С 2 R
R
О1
О1
H
So R
2
Sб 2 R H
О
S п 2 R H 2 R 2 R ( H R)
2
О
R

6.

Сечение цилиндра
плоскостью,
параллельной его оси
О1
Сечение цилиндра
плоскостью, перпендикулярной его оси
О1
А1
О2
О
О
А

7.

Цилиндрическая гастрономия

8.

9.

Цилиндрическая архитектура

10.

Найдите площадь поверхности (внешней и
внутренней) шляпы, размеры которой (в см)
указаны на рисунке.
Решение.
1) Если дно шляпы опустить на
плоскость её полей, то получим
круг радиуса R = r1+ 10 = 20 cм.
r1=10
10
10
2) Площадь этого круга
So R 2 400 (см2 ).
3) Найдем площадь боковой поверхности цилиндрической части
Sб Сокр h 2 r1 h 2 10 10 200 (см2 ).
4) Найдем площадь шляпы
Sшляпы 2 (Sкруга Sб ) 2 (400 200 ) 1600 (см2 ).
Ответ: 1600 (см2).

11.

№523
Осевое сечение цилиндра – квадрат,
диагональ которого равна 20 см. Найдите:
а) высоту цилиндра; б) So цилиндра
Решение.
B
C
1. Проведем диагональ АС
сечения АВСD.
2. ADC – равнобедренный,
прямоугольный, АD=DC, h = 2r,
45
20
CAD = ACD=45 , тогда
2
h AC cos 45 20
10 2 .
2
3. Найдем радиус основания
45
A
D
4. Найдем площадь основания
Ответ: а )10 2 ;
б )50 .
h 10 2
r
5 2.
2
2
2
So r 5 2 50 .
2

12.

Площадь осевого сечения цилиндра
равна 10 м2, а площадь основания – 5 м2.
Найдите высоту цилиндра.
№525
C
Решение.
1. Площадь основания – круг,
B
So r 2 , тогда r S 5 .
2. Площадь сечения – прямоугольник,
Sc AB BC h 2r , тогда
D
A
r
Sc
5
h
10 2
5
5 .
2r
5
Ответ:
5 .

13.

№527
В
Концы отрезка АВ лежат на разных основаниях цилиндра.
Радиус цилиндра равен r, его высота – h, расстояние между
прямой АВ и осью цилиндра равно d. Найдите: a) высоту,
если r = 10, d = 8, AB = 13.
1. Построим отрезок АВ.
Решение.
2. Проведем радиус АО.
3. Построим отрезок d.
4. Отрезок ОК – искомое расстояние.
5. Из прямоугольного АОК находим:
a
AK r 2 d 2 100 64 6,
С
К
А
значит АС = 12.
6. Из прямоугольного АВС находим:
d r
ВС АВ 2 АС 2 169 144 5.
r
Итак, h = 5.
Ответ: 5.

14.

№532
Через образующую АА1 цилиндра проведены две
секущие плоскости, одна из которых проходит через ось
цилиндра. Найдите отношение площадей сечений
цилиндра этими плоскостями, если угол между ними
равен .
Решение.
В
A
1) Сделаем чертеж, построим
плоскости АА1В1В и АА1С1С.
2) Составим отношение площадей
AA1 AB AB
сечений S ABB1 A1
C
S ACC1 A1
AA1 AC
AC
.
3) Построим плоскость ВВ1С1С.
В1
А1
1
Ответ:
.
cos
4) Заметим, что АВ диаметр основания
цилиндра, значит АСВ=90 , тогда
AC AB cos .
C1
5) Итак,
S ABB1 A1
S ACC1 A1
AB
AB
1
.
AC AB cos cos

15.

Плоскость , параллельная оси
цилиндра, отсекает от окружности
основания дугу AmD с градусной
мерой . Радиус цилиндра равен a,
высота равна h, расстояние между
осью цилиндра ОО1 и плоскостью
равно d.
1) Докажите, что сечение
цилиндра плоскостью
есть прямоугольник.
1) Составьте план
вычисления площади
сечения по данным , h, d.
2) Найдите AD, если
a = 10 см, = 60 .
2) Найдите AD, если
a = 8 см, = 120 .
Ответ: 10
Ответ: 8
3

16.

Домашнее задание
Повторить стр.130-132, гл. 1, п.59-60,
№530, № 537.
Рефлексия
Что нового вы узнали на уроке?
Чему вы научились?
Какое у вас настроение в конце урока?
Можете ли вы объяснить решение данных
задач однокласснику, пропустившему урок
сегодня?