Similar presentations:
Моменты инерции при повороте осей координат. Главные оси и главные моменты инерции. Определение геометрических характеристик
1.
Санкт-Петербургский государственныйархитектурно-строительный университет
кафедра Строительной механики
Тема 5
Моменты инерции при повороте осей координат
Главные оси и главные моменты инерции
Примеры определения геометрических характеристик
Авторы:
к.т.н., Войтко Александр Михайлович
к.т.н., Алейник Вадим Иванович
1
2.
3.4. Моменты инерции при повороте осей координат1. Формулы преобразования координат.
y1 y cos z sin ;
z1 z cos y sin .
(6.1)
2. Осевые моменты инерции.
I y1 z dA z cos y sin dA
2
2
1
A
2
A
z cos2 2 yz cos sin y 2 sin 2 dA cos2 z 2 dA
A
A
(6.2)
2cos sin yzdA sin 2 y 2 dA
A
A
I y cos2 I yz 2sin cos I z sin 2 .
2
3.
С учетомI y1 I y cos2 I z sin 2 I yz sin 2 .
(6.3)
I z1 y dA y cos z sin dA
2
2
1
A
2
A
y cos2 2 yz cos sin z 2 sin 2 dA cos 2 y 2 dA
A
A
2cos sin yzdA sin 2 z 2 dA
A
(6.4)
A
I z cos2 I yz 2sin cos I y sin 2 .
I z1 I z cos2 I y sin 2 I yz sin 2 .
(6.5)
3
4.
1 cos 21 cos 2
2
cos
, sin
.
2
2
2
(6.6)
С учетом (6.6) формулы (6.3) и (6.5) получают вид
1 cos 2
1 cos 2
Iz
I yz sin 2
2
2
I y Iz I y Iz
cos 2 I yz sin 2 .
2
2
I y1 I y
1 cos 2
1 cos 2
I z1 I z
Iy
I yz sin 2
2
2
I y Iz Iz I y
cos 2 I yz sin 2 .
2
2
(6.7)
(6.8)
4
5.
Сложим левые и правые части формул (6.7) и (6.8):I y1 I z1 I y I z .
(6.9)
Свойство осевых моментов инерции:
при повороте координатных осей сумма моментов инерции относительно
двух взаимно ортогональных осей не меняется.
3. Центробежный момент инерции.
I y1z1 y1 z1dA y cos z sin z cos y sin dA
A
A
z 2 sin cos y 2 sin cos yz cos 2 sin 2 dA
(6.10)
A
I y I z sin cos I yz cos 2 sin 2 .
5
6.
2sin cos sin 2 ; cos2 sin 2 cos 2 .(6.11)
Формула (6.10) принимает вид с учетом (6.11):
I y1 z1
I y Iz
2
sin 2 I yz cos 2 .
(6.12)
При α = 90°:
I y1z1 I yz .
(6.13)
Свойство центробежных моментов инерции:
при повороте координатных осей на 90° центробежный момент
инерции сохраняет свою величину и меняет знак.
6
7.
Формулы для осевых и центробежных моментов инерциипри повороте осей координат:
I y1
I z1
I y Iz
2
I y Iz
I y1z1
2
I y Iz
2
I y Iz
2
Iz I y
2
cos 2 I yz sin 2 .
cos 2 I yz sin 2 .
(6.14)
sin 2 I yz cos 2 .
7
8.
3.5. Главные оси и главные моменты инерции1. Оси, относительно которых центробежный момент
инерции равен нулю, называются главными.
2. Если начало координат совпадает с центром
тяжести, оси называются главными центральными.
3. Оси симметрии сечения всегда являются главными
центральными осями.
4. Моменты инерции относительно главных центральных осей
называются главными центральными моментами инерции.
5. Главные моменты инерции являются экстремальными
осевыми моментами инерции.
8
9.
Определение положения главных центральных осей инерцииПриравняем к нулю выражение (6.12):
I y1z1
Отсюда:
I y Iz
2
tan 2
sin 2 I yz cos 2 0 ,
2 I yz
I y Iz
.
(6.15)
(6.16)
Условие экстремума Iy1 (6.7):
dI y1
d
I y Iz
2
2sin 2 2 I yz cos 2 0 .
(6.17)
9
10.
tan 22 I yz
I y Iz
(6.18)
.
Формулы (6.16) и (6.18) совпадают.
Осевые моменты инерции относительно главных центральных осей имеют
экстремальные значения.
Определение величин главных центральных моментов инерции
Тригонометрические соотношения:
cos 2
1
1 tan 2
2
; sin 2
tan 2
1 tan 2
2
.
(6.19)
10
11.
Подставим (6.18) в (6.19):1
cos 2
1
4I
I I
y
sin 2
2
yz
2
I y Iz
2
I
I
4
I
y z yz
2
;
(6.20)
z
2 I yz
2
I
I
4
I
y z yz
2
.
(6.21)
(6.20) и (6.21) подставим в (6.7):
11
12.
I y1I y Iz
2
I y Iz
2
I y Iz
2
2
I y Iz
2
cos 2 I yz sin 2
1
I I 4I
2
y
I y Iz
2
z
I I 4I
2 I I 4I
2
y
2
yz
z
2
y
z
2
yz
2
yz
I y Iz
2
2 I yz2
I I 4I
2
y
1
2
z
2
yz
(6.22)
I I 4I .
2
y
z
2
yz
Величины главных моментов инерции:
I гл
I y Iz
2
1
2
2
I
I
4
I
y z yz .
2
(6.23)
12
13.
Положение главных осей инерции:2 I yz
, 2 0 arctan
tan 2 0
.
I y Iz
I y Iz
2 I yz
1
0 arctan
.
I I
2
y z
2 I yz
(6.24)
Величины главных моментов инерции через формулы для моментов инерции при повороте
осей:
I гл1
I y Iz
2
I y Iz
2
cos 2 0 I yz sin 2 0 .
(6.25)
Из свойства постоянства суммы моментов инерции (6.9):
I max I min I y I z .
(6.26)
13
14.
Отсюда:I гл2 I y I z I гл1 .
(6.27)
Максимальные центробежные моменты инерции
I yz 0
y и z ‒ главные центральные оси.
Из (6.12):
I y1z1
I y Iz
I ymax
1z1
sin 2 .
(6.28)
.
(6.29)
2
I y Iz
2
Максимальный центробежный момент инерции равен полуразности
главных осевых моментов инерции
Оси относительно которых центробежный момент инерции максимален по
величине, повернуты под углом 45º по отношению к главным осям.
14
15.
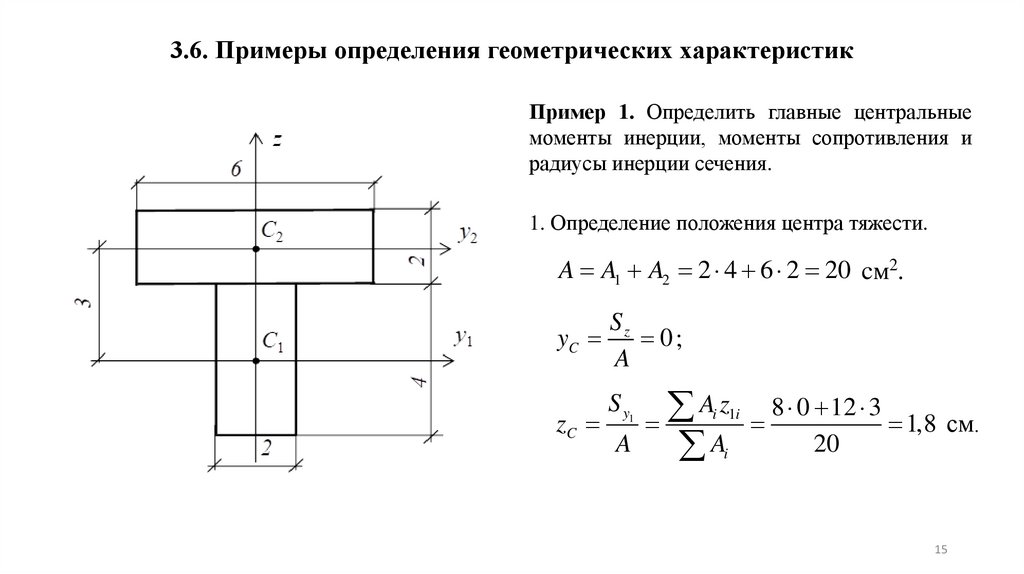
3.6. Примеры определения геометрических характеристикПример 1. Определить главные центральные
моменты инерции, моменты сопротивления и
радиусы инерции сечения.
1. Определение положения центра тяжести.
A A1 A2 2 4 6 2 20 cм2.
Sz
yC
0;
A
Az
8 0 12 3
z
1,8 см.
A
20
A
S y1
i 1i
C
i
15
16.
2. Определение главных моментов инерции.Координаты центров тяжести в центральной
системе осей x и y:
a1 a2 0 ; b1 1,8 см; b2 1, 2 см.
Главные центральные моменты инерции:
3
3
4
2
2
6
I z I zi ai2 Ai
0
0 36,87 см4.
12
12
i
3
3
2
4
6
2
I y I yi bi2 Ai
1,82 8
1,22 12 57,87 см4.
12
12
i
16
17.
3. Определение осевых моментов сопротивления сечения.Максимальные расстояния от главных осей до контура сечения:
ymax 3 см; zmax 3,8 см.
Осевые моменты сопротивления:
Iy
57,87
Wy
15,23 см3;
zmax
3,8
Iz
38,67
Wz
12,89 см3.
ymax
3
4. Вычисление радиусов инерции сечения.
iy
Iy
57,87
1,7 см;
A
20
iz
Iz
38,67
1,4 см.
A
20
17
18.
Пример 2. Определить главные центральныемоменты инерции и радиусы инерции сечения.
1. Определение положения центра тяжести.
A1 18 2 36 см2; A2 15 2 30 см2.
A A1 A2 36 30 66 см2.
y11 0 ; y12 6,5 см; z11 0 ; z12 10 см.
Ay
36 0 30 6,5
y
2,95 см
A
66
A
S z1
i 1i
C
i
Az
36 0 30 10
z
4,55 см.
A
66
A
S y1
i 1i
C
i
18
19.
Координаты центров тяжести в центральнойсистеме осей x0 и y0:
a1 y11 yC 0 2,95 2,95 см.
a2 y12 yC 6,5 2,95 3,55 см.
b1 z11 zC 0 4,55 4,55 см.
b2 z12 zC 10 4,55 5,45 см.
2. Центральные осевые моменты инерции.
I y0 I yi bi2 Ai ; I z0 I zi ai2 Ai .
i
i
2 183
15 23
2
I y0
4,55 36
5,452 30 2618,4 см4.
12
12
3
18 23
2
15
I z0
2,952 36
3,552 30 1265,9 см4.
12
12
19
20.
3. Центробежный момент инерции.I y0 z0 I yi zi ai bi Ai 2,95 4,55 36 3,55 5,45 30 1074,3
i
см4.
4. Положение главных осей инерции.
tan 2 0
2 I y0 z0
I y0 I z0
2 1074,3
2618, 4 1265,9
1,59 .
2 57 30 ; 28 45 .
5. Главные центральные моменты инерции.
I y0 I z0
2
1
I гл
I y0 I z0 4 I y20 z0
2
2
2618,4 1265,9 1
2
2
2618,4 1265,9 4 1074,3 .
2
2
20
21.
I max 3211 см4; I min 673 см4.Iy
I y0 I z0
I y0 I z0
cos 2 0 I yz sin 2 0
2
2
2618,4 1265,9 2618,4 1265,9
0,537 1074,3 0,843
2
2
= 3211 см4.
I y I max .
I z I min .
Проверка постоянства суммы моментов инерции.
I max I min I y0 I z0 . 3211 673 2618 1266 3884 см4.
21
22.
Санкт-Петербургский государственныйархитектурно-строительный университет
кафедра Строительной механики
Авторы:
к.т.н., Войтко Александр Михайлович
к.т.н., Алейник Вадим Иванович
tehmeh@spbgasu.ru
22





















 mathematics
mathematics








