Определение геометрических характеристик плоского составного симметричного сечения. Практическое занятие

1.

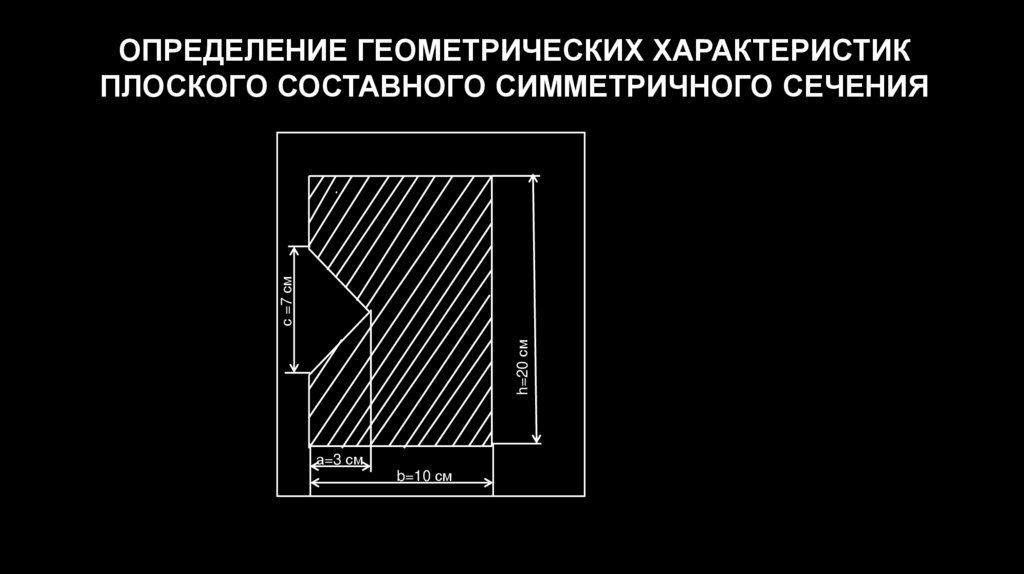
h=20 см
с =7 cм
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК
ПЛОСКОГО СОСТАВНОГО СИММЕТРИЧНОГО СЕЧЕНИЯ
а=3 см
b=10 см

2.

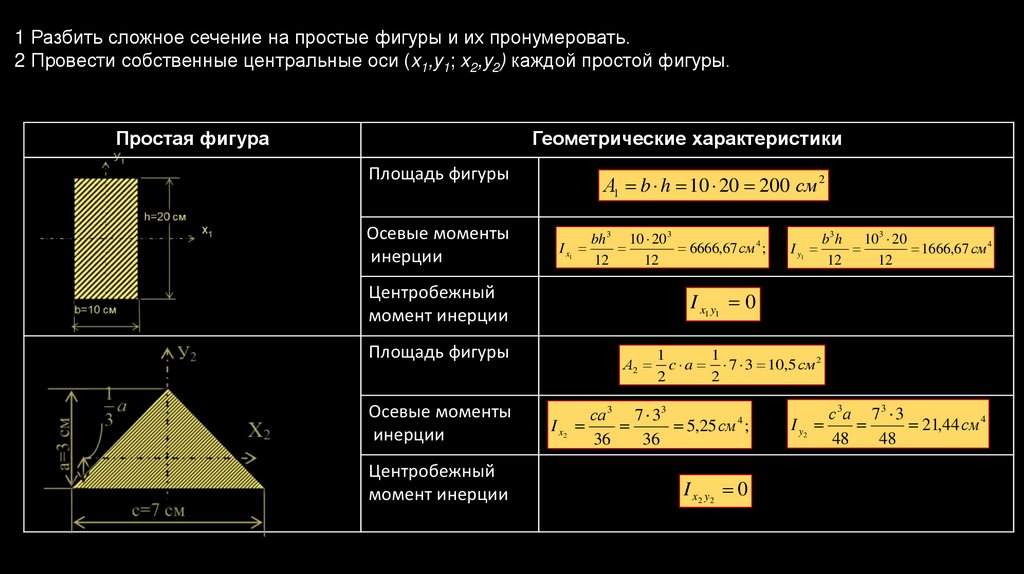
1 Разбить сложное сечение на простые фигуры и их пронумеровать.
2 Провести собственные центральные оси (x1,y1; x2,y2) каждой простой фигуры.
Простая фигура
Геометрические характеристики
Площадь фигуры
А1 b h 10 20 200 см 2
Осевые моменты
инерции
bh 3 10 20 3
I x1
6666,67 см 4 ;
12
12
Центробежный
момент инерции
I x1 y1 0
Площадь фигуры
А2
b 3 h 103 20
I y1
1666,67 см 4
12
12
1
1
c a 7 3 10,5 см 2
2
2
Осевые моменты
инерции
сa 3 7 33
I x2
5,25 см 4 ;
36
36
Центробежный
момент инерции
I x2 y 2 0
с 3а 73 3
I y2
21,44 см 4
48
48

3.

2 Координаты центров тяжестей простых фигур относительно
вспомогательных осей
x 0 см; y 0
у2
Yc у1 V, min
b1=0,22 cм
22 см
x 0 см; y b2=4,
0
1
b 1
10 1
x 2 a 3 4 см;
2 3
2 3
y 2 0.
3 Координаты центра тяжести рассматриваемого сечения
у1
х1, х2
Хс=0,22 см
х2=4 см
iv=2,8 cм iv=2,8 cм
а=3 см
b=10 см
xc
4 Осевые и центробежный моменты инерции сечения
х1, х2,
Хс
U, max
I xc ( I x1 a12 A1 ) ( I x2 a 22 A2 ) 6666,67 21,44 6645,23 см 4 ;
I yc ( I y1 b12 A1 ) ( I y2 b22 A2 ) (1666,67 0,22 2 200) (5,25 4,22 2 10,5) 1484,11см 4 ;
I xc y x 0
a1 у1 уC 0;
b1 х1 хc 0 0,22 0,22 см;
a2 у2 уC 0;
b2 х2 хс 4 0,22 4,22 см.
5 Главные моменты инерции сечения
4
4
I xc > I yc I max I u 6645,23 см , I min I v 1484,11см ,
6 Главные радиусы инерции
х1, у1 – вспомогательные оси
x1 A1 x 2 A2 0 200 ( 4) 10,5
0,22 см;
A1 A2
200 10,5
y c 0.
h=20 см
С1С
с1
с2
С2
1
b 1
10 1
x2 ( a ) ( 3) 4 см;
2 3
2 3
iu=5,9 cм
с =7 cм
у2
1
y 2 0.
iu=5,9 cм
1
iu
Iu
6645,23
5,9 см,
A
189,5
iv
Iv
1484,11
2,8 см.
A
189,5

4.

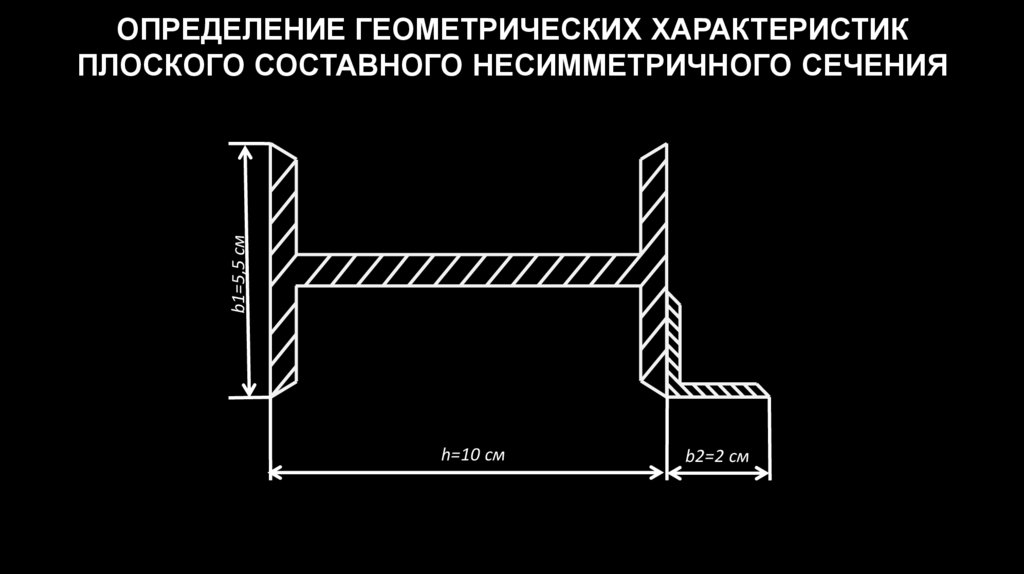
b1=5,5 см
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК
ПЛОСКОГО СОСТАВНОГО НЕСИММЕТРИЧНОГО СЕЧЕНИЯ
h=10 cм
b2=2 cм

5.

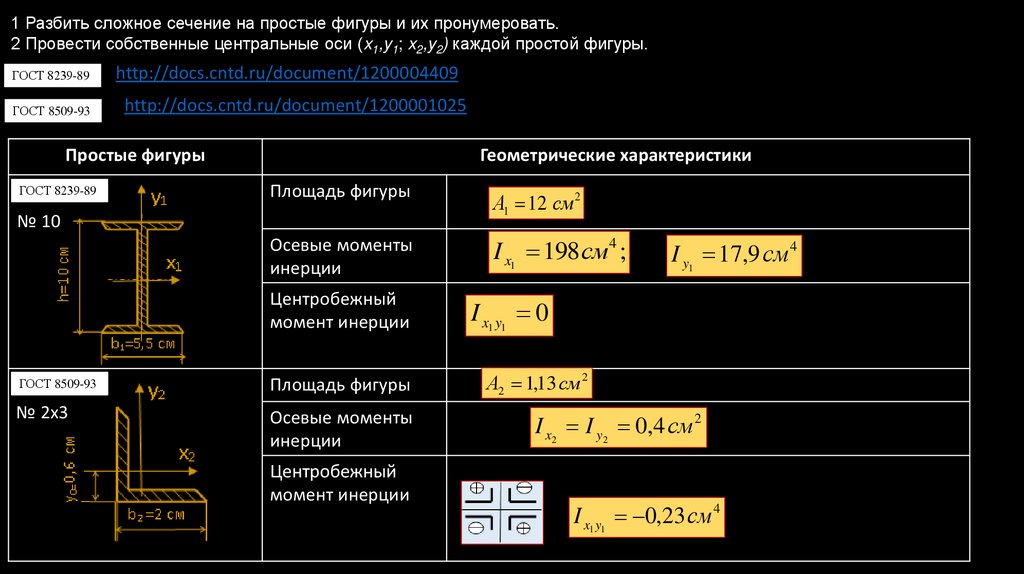
1 Разбить сложное сечение на простые фигуры и их пронумеровать.
2 Провести собственные центральные оси (x1,y1; x2,y2) каждой простой фигуры.
ГОСТ 8239-89
http://docs.cntd.ru/document/1200004409
ГОСТ 8509-93
http://docs.cntd.ru/document/1200001025
Простые фигуры
ГОСТ 8239-89
Геометрические характеристики
Площадь фигуры
А1 12 см 2
Осевые моменты
инерции
I x1 198 см 4 ;
№ 10
Центробежный
момент инерции
ГОСТ 8509-93
Площадь фигуры
№ 2х3
Осевые моменты
инерции
Центробежный
момент инерции
I y1 17,9 см 4
I x1 y1 0
А2 1,13 см 2
I x2 I y2 0,4 см 2
I x1 y1 0,23 см 4

6.

Yc
Y
у1
с1=0,5 см
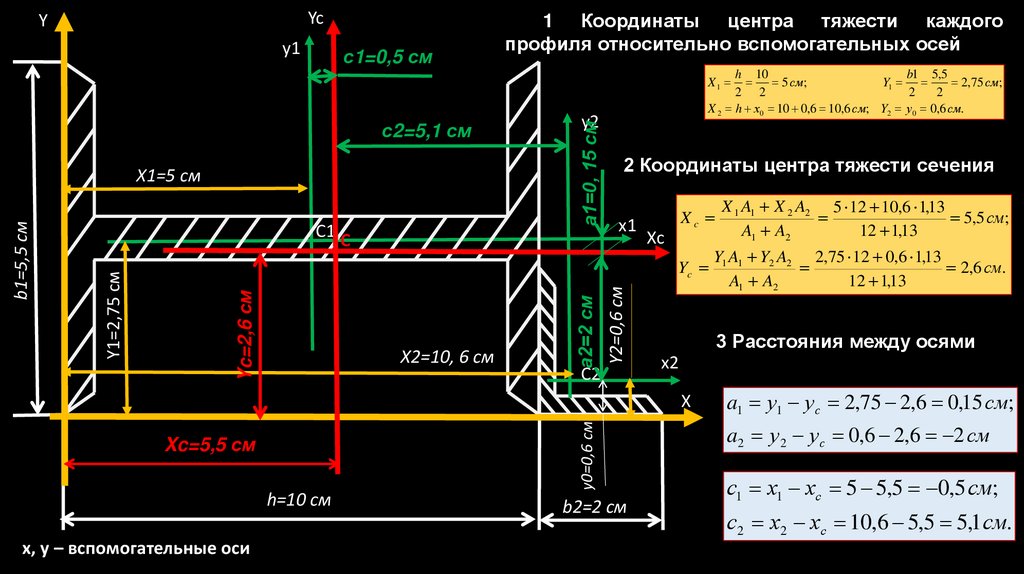
1 Координаты центра тяжести каждого
профиля относительно вспомогательных осей
h 10
b1 5,5
5 см;
Y1
2,75 см;
2 2
2
2
X 2 h х0 10 0,6 10,6 см; Y2 у0 0,6 см.
X1
С1 С
2 Координаты центра тяжести сечения
х1
Xc
Хс
Y2=0,6 см
Х2=10, 6 см
а2=2 см
Yc
Yc=2,6 см
Y1=2,75 см
b1=5,5 см
Х1=5 см
у2
а1=0, 15 см
с2=5,1 см
С2
х2
х, у – вспомогательные оси
a1 у1 ус 2,75 2,6 0,15 см;
y0=0,6 см
h=10 cм
Y1 A1 Y2 A2 2,75 12 0,6 1,13
2,6 см.
A1 A2
12 1,13
3 Расстояния между осями
Х
Xc=5,5 см
X 1 A1 X 2 A2 5 12 10,6 1,13
5,5 см;
A1 A2
12 1,13
a2 у2 ус 0,6 2,6 2 см
b2=2 cм
с2 х2 хс 10,6 5,5 5,1 см.
с1 х1 хс 5 5,5 0,5 см;

7.

I y c I xc
Yc
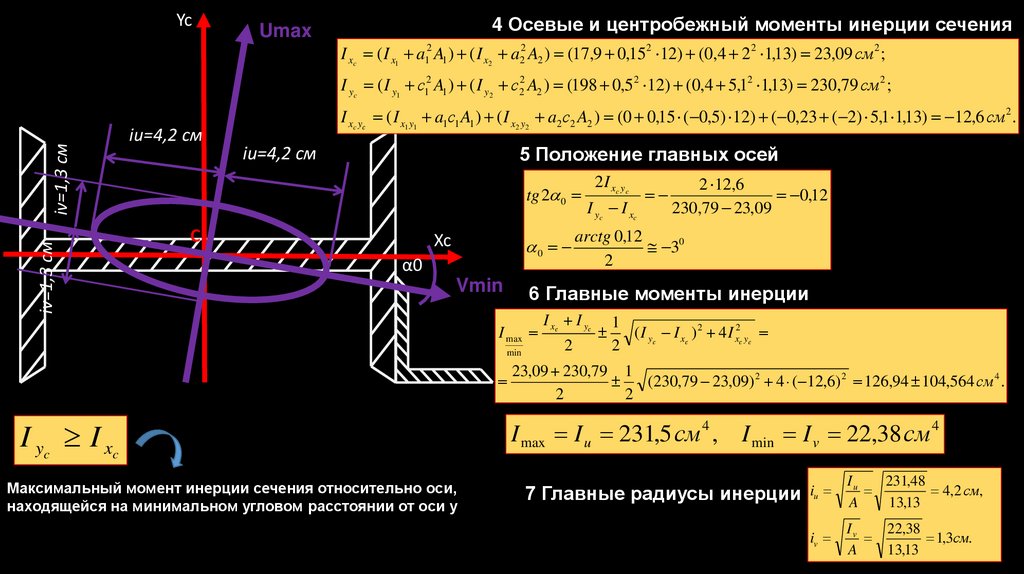
4 Осевые и центробежный моменты инерции сечения
Umax
I xc ( I x1 a12 A1 ) ( I x2 a22 A2 ) (17,9 0,152 12) (0,4 2 2 1,13) 23,09 см 2 ;
iv=1,3 см
iv=1,3 см
I yc ( I y1 с12 A1 ) ( I y2 с22 A2 ) (198 0,52 12) (0,4 5,12 1,13) 230,79 см 2 ;
iu=4,2 см
I xc yс ( I x1 y1 a1с1 A1 ) ( I x2 y2 a2 с2 A2 ) (0 0,15 ( 0,5) 12) ( 0,23 ( 2) 5,1 1,13) 12,6 см 2 .
5 Положение главных осей
iu=4,2 см
tg 2 0
С
Хс
0
α0
Vmin
min
Максимальный момент инерции сечения относительно оси,
находящейся на минимальном угловом расстоянии от оси у
I y c I xc
2 12,6
0,12
230,79 23,09
arctg 0,12
30
2
6 Главные моменты инерции
I max
I y c I xc
2 I xc y c
I xс I y с
2
1
( I yс I xс ) 2 4 I x2с yс
2
23,09 230,79 1
(230,79 23,09) 2 4 ( 12,6) 2 126,94 104,564 см 4 .
2
2
I max I u 231,5 см 4 , I min I v 22,38 см 4
7 Главные радиусы инерции iu
iv
Iu
231,48
4,2 см,
A
13,13
Iv
22,38
1,3см.
A
13,13