Similar presentations:
Геометрические характеристики поперечных сечений
1. Лекция 6,7,8
2.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙГеометрические характеристики плоских фигур –
это площадь, ее статические моменты и моменты
инерции: осевые, полярный, центробежный.
3.
Геометрические характеристики плоских фигур.Параметры, определяемые по формулам
yC А ydА
хC А хdА;
А
А
называются статическими моментами площади
плоской фигуры относительно осей
уC
х
А
у
хC
S x y dA
A
A
Они используются для определения положения центра тяжести плоской фигуры
хC
C
уC
у
S y x dA;
х
и равны нулю относительно
осей, проведенных через
центр тяжести плоской фигуры (центральных осей).
4.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙПо теореме о моменте равнодействующей имеем
S x yС А
S у хС А
где хС, уС - координаты центра тяжести фигуры;
- площадь всей фигуры.
Sx
yС
А
хС
Sу
А
А
5.
Геометрические характеристики плоских фигур.Кроме площади и статических моментов к геометрическим характеристикам плоских фигур относятся моменты инерции: осевые, полярный, центробежный.
Вообще, для твердых тел момент инерции – это
величина, характеризующая распределение масс в
теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении:
2
2
I х у dV
I y x dV
V
V
I хy x уdV
V
6.
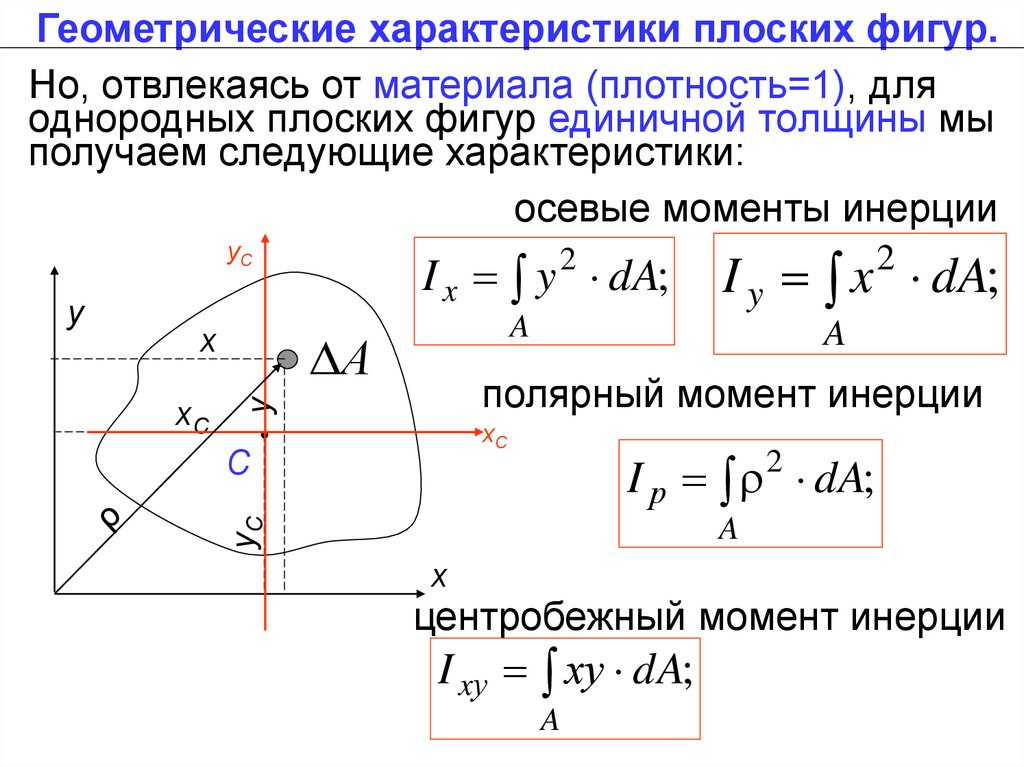
Геометрические характеристики плоских фигур.Но, отвлекаясь от материала (плотность=1), для
однородных плоских фигур единичной толщины мы
получаем следующие характеристики:
осевые моменты инерции
уC
х
А
I y x dA;
2
A
полярный момент инерции
у
хC
A
хC
C
I р dA;
2
уC
у
I x y dA;
2
A
х
центробежный момент инерции
I xу хy dA;
A
7.
Геометрические характеристики плоских фигур.Свойства некоторых моментов инерции заключаются в следующем.
Осевые моментов инерции всегда положительны.
Сумма осевых моментов инерции равна полярному
моменту инерции.
Моменты инерции, определяемые относительно
центральных осей, называются центральными.
Центральные оси, относительно которых
центробежный момент инерции равен нулю,
называются главными.
Ось симметрии для фигуры является главной осью
8.
Геометрические характеристики плоских фигур.Во многих расчетах на прочность используются эти
характеристики.
Для простейших фигур по приведенным формулам
выведены расчетные формулы для определения
величины центральных моментов инерции.
b
Прямоугольник
h
у
x
bh3
Ix
12
b3h
Iy
12
I yх 0.
9.
Геометрические характеристики плоских фигур.Треугольник
b
bh3
Ix
36
у1
1
x1
h
b3h
Iy
36
I yх
b2h2
.
72
10.
Геометрические характеристики плоских фигур.Круг
у
x
d
d
Ix Iy
;
64
I yх 0.
4
11.
Геометрические характеристики плоских фигур.Зная центральные моменты инерции простых фигур
можно определить эти характеристики относительно
других осей, используя формулу параллельного
переноса осей:
Момент инерции относительно любой оси
равен моменту инерции относительно
центральной оси, параллельной данной,
плюс произведение площади фигуры на
квадрат расстояния между осями.
12.
Геометрические характеристики плоских фигур.Формулы поворота осей
ν
у
u
х
у
u х cos y sin
v y cos х sin
u
ν
α
х
Iu I x cos2 I y sin2 I xy cos 2
Iv I x sin2 I y cos2 I xy cos 2
Iuv
Ix Iy
2
sin 2 I xy cos 2
tg 2
2I y C xC
I xC I y C
13.
Геометрические характеристики плоских фигур.При определении этих величин для фигур, имеющих
сложные очертания, применяют метод разбиения их
на простейшие фигуры.
Момент инерции сложной фигуры равен сумме
моментов инерции ее составных частей:
I x I x1 I x 2 I x3
I y I y1 I y I y 3
2
I хy I yх1 I yх I yх3
2
14.
Геометрические характеристики плоских фигур.При определении главных осей, если угол положительный, поворот осей производится против часовой стрелки.
Осевые моменты относительно главных осей называются главными и имеют экстремальные значения
Их можно определить по формуле
max
I min
I xC I y C
2
1
( I xC I yC )2 4I y2C xC
2
15.
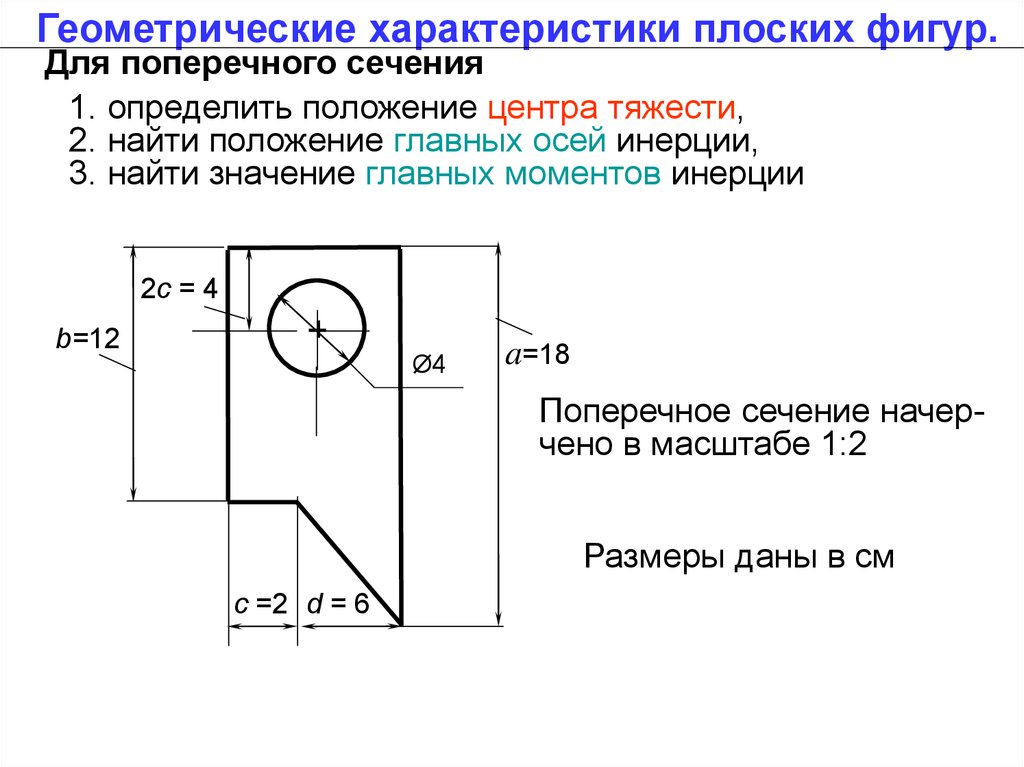
Геометрические характеристики плоских фигур.Для поперечного сечения
1. определить положение центра тяжести,
2. найти положение главных осей инерции,
3. найти значение глaвныx моментов инерции
2с = 4
b=12
Ø4
a=18
Поперечное сечение начерчено в масштабе 1:2
Размеры даны в см
с =2 d = 6
16.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙРазбиваем сечение на простейшие фигуры:
1– прямоугольный треугольник,
2 - прямоугольник,
3 – круг
2с = 4
3
C3
b=12
C2
2
a=18
1
с=2
d =6
C1
С1, С2, С3 –центры тяжести
фигур
17.
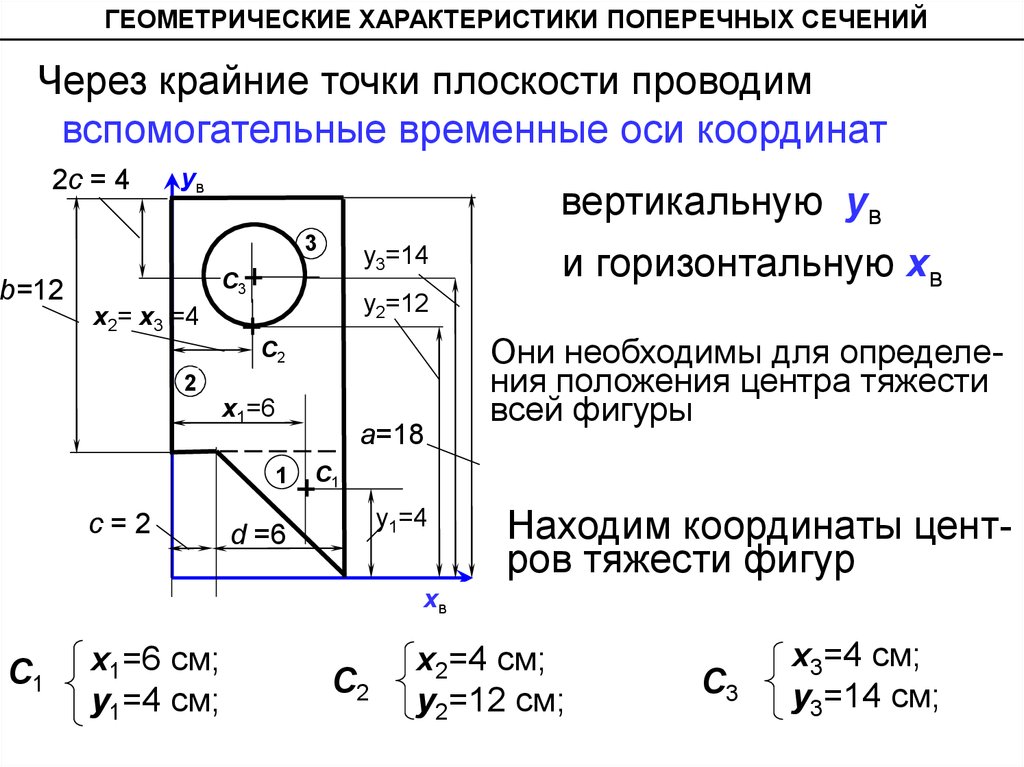
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙЧерез крайние точки плоскости проводим
вспомогательные временные оси координат
2с = 4
ув
вертикальную ув
3
у3=14
C3
b=12
у2=12
x2= x3 =4
C2
2
x1=6
1
с=2
a=18
и горизонтальную хв
Они необходимы для определения положения центра тяжести
всей фигуры
C1
у1=4
d =6
Находим координаты центров тяжести фигур
xв
C1
x1=6 см;
у1=4 см;
C2
x2=4 см;
у2=12 см;
C3
x3=4 см;
у3=14 см;
18.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ2с = 4
Определяем
площади
b1=6 см
ув
⅓b1
3
⅓h1
1
Ø4
b=12
h1=6см
2
b2=8 см
a=18
А1=½ b1 h1=
=½ 6·6=18 см2
1
с=2
2
d =6
h2=12см
xв
3
Ø4
А3 = πd2/4=
=3,14·42/4= 12,56см2
А2 = b2 h2=
=8·12=96 см2
А = А1+ А2 - А3=18+96-12,56=101,44 см2
19.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ2с = 4
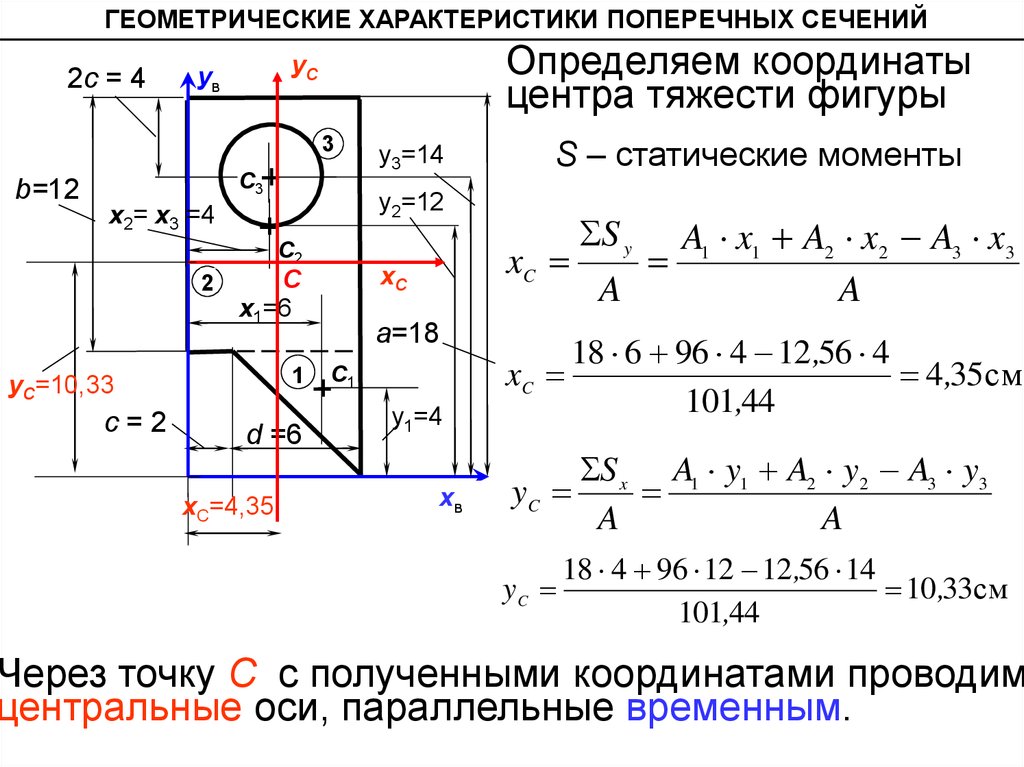
Определяем координаты
центра тяжести фигуры
уС
ув
3
C3
b=12
у2=12
x2= x3 =4
C2
2
С
x1=6
1
уС=10,33
с=2
d =6
xС=4,35
у3=14
xС
a=18
C1
у1=4
xв
S – статические моменты
S y
A1 x1 A2 x2 A3 x3
xC
A
A
18 6 96 4 12 ,56 4
xC
4,35см
101,44
S x A1 y1 A2 y2 A3 y3
yC
A
A
18 4 96 12 12 ,56 14
yC
10 ,33см
101,44
Через точку С с полученными координатами проводим
центральные оси, параллельные временным.
20.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙl2= l3= -0,35
ув
x2= x3 =4
3
а3=3,67
C3
а2=1,67
у3=14
у2=12
C2
2
С
x1=6
xС
а1=-6,33
1
C1
у1=4
уС=10,33
xС=4,35
l1=1,65
xв
а2 =12- 10,33=1,67см
C2 l = 4-4,35=-0,35 см
2
Определим координаты центров
тяжести простейших фигур относительно центральных осей (в
новой системе координат)
Они отражают расстояния
между центральными осями и
соответствующими осями
простейших фигур
a - расстояния между осями х
l – расстояния между осями у
а = у- уС
l= x- xС
а1 = 4-10,33=-6,33 см
C1 l = 6-4,35=1,65 см
1
C3
а3 =14-10,33=3,67см
l3= 4-4,35=-0,35 см
21.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙОпределим моменты инерции простейших фигур
относительно их центральных осей
b1=6 см
у1
1
I x1
6 63
36 см4 ;
36
36
I y1
b13 h1 63 6
36 см4 ;
36
36
x1
h1=6см
2
3
b1h1
2
2
2
b1 h1
61 61
I y1 х
18см4
1
72
72
22.
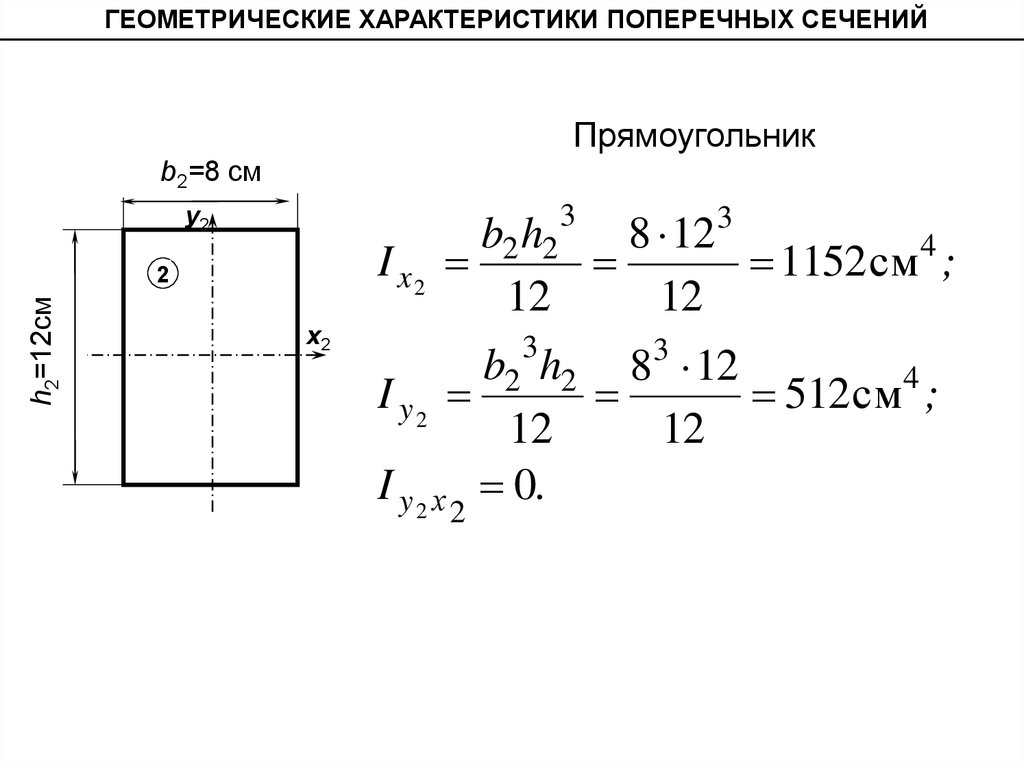
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙПрямоугольник
b2=8 см
у2
I x2
2
h2=12см
b2 h2
8 12 3
1152 см4 ;
12
12
3
x2
b2 h2 83 12
I y2
512 см4 ;
12
12
I y 2 х 0.
3
2
23.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙКруг
у3
d 3,14 4
4
I x3 I y 3
12 ,56см ;
64
64
I y3 х 0.
4
3
x3
Ø4
3
4
24.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙОпределим моменты инерции всего сечения относительно центральных осей:
Момент инерции сложной фигуры равен сумме
моментов инерции ее составных частей:
I xС I xС I xС 2 I xС 3
1
I yС I yС I yС I yС 3
1
2
I y С хС I y С
х
1 С1
I yС
х
2 С2
I yС
х
3 С3
25.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙМоменты инерции составных частей найдем,
используя формулу параллельного переноса осей:
Момент инерции относительно любой оси
равен моменту инерции относительно
центральной оси, параллельной данной,
плюс произведение площади фигуры на
квадрат расстояния между осями.
26.
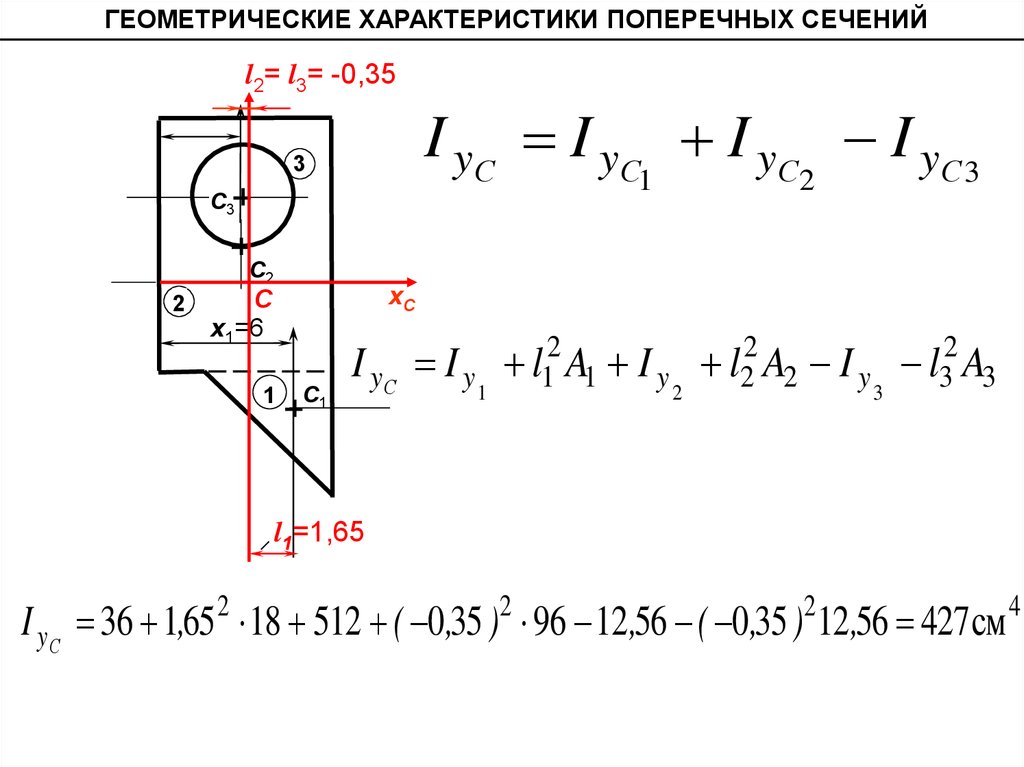
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙI xС I xС I xС 2 I xС 3
а3=3,67
а2=1,67
1
3
C3
C2
2
С
x1=6
1
xС
C1
а1=-6,33
I xС I x1
2
a1 A1
I x2
2
a2 A2
2
I x3 a3 A3
I xС 36 ( 6,332 18 ) 1152 1,67 2 96 12 ,56 3,67 2 12 ,56 1995 ,2см 4
27.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙl2= l3= -0,35
I yС I yС I yС I yС 3
3
1
C3
C2
2
С
x1=6
2
xС
1
C1
I yС
2
I y l1 A1
1
Iy
2
2
l2 A2
2
I y l3 A3
3
l1=1,65
I yС 36 1,65 2 18 512 ( 0,35 )2 96 12 ,56 ( 0,35 )212 ,56 427 см 4
28.
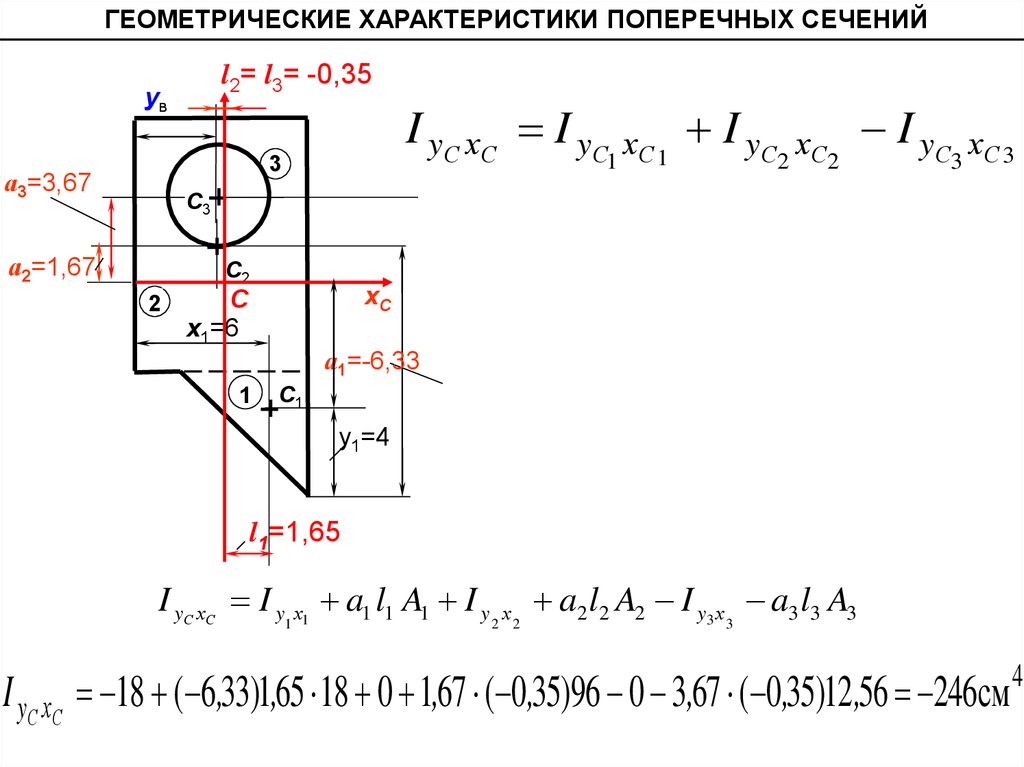
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙl2= l3= -0,35
ув
I y С хС I y С
х
1 С1
3
а3=3,67
I yС
х
2 С2
I yС
х
3 С3
C3
а2=1,67
C2
2
С
x1=6
xС
а1=-6,33
1
C1
у1=4
l1=1,65
I yС хС I y х1 a1 l1 A1 I y
1
х
2 2
a2 l2 A2 I y3 х a3 l3 A3
3
I yС хС 18 ( 6,33)1,65 18 0 1,67 ( 0,35)96 0 3,67 ( 0,35)12,56 246см 4
29.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙФормулы поворота осей
ν
у
u
х
у
u х cos y sin
v y cos х sin
u
ν
α
х
Iu I x cos2 I y sin2 I xy cos 2
Iv I x sin2 I y cos2 I xy cos 2
Iuv
Ix Iy
2
sin 2 I xy cos 2
tg 2
2I y C xC
I xC I y C
30.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙПолучили центробежный момент инерции сечения
отличным от нуля, следовательно, оси xС уС не
являются главными осями инерции.
Найдем положение главных осей инерции. Угол
поворота осей определим по формуле:
tg 2
2 I y C xC
I xC I y C
2( 246 )
tg 2
0,3137 ;
1995 ,2 427
2 17 ,4 ;
8,7 .
При знаке «+» поворот выполняется против часовой
стрелки, если«-», то поворот а направлении часовой
стрелки
31.
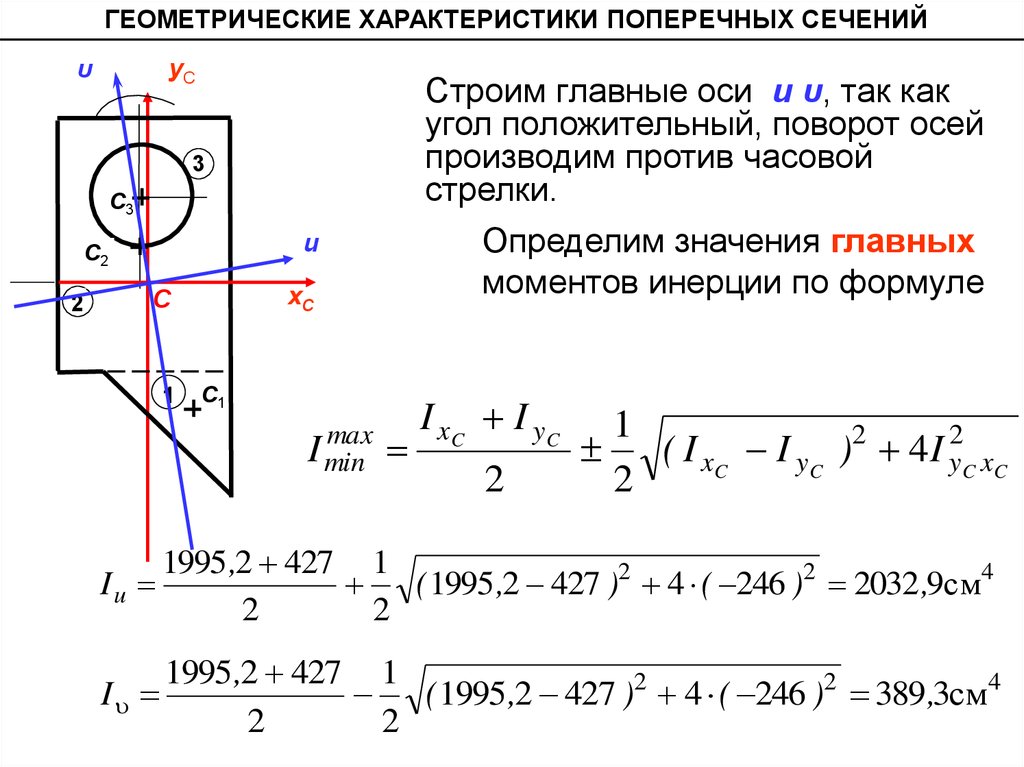
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙуС
υ
Строим главные оси u υ, так как
угол положительный, поворот осей
производим против часовой
стрелки.
Определим значения главных
моментов инерции по формуле
3
C3
u
C2
2
С
1
xС
C1
max
I min
I xC I y C
2
1
( I xC I yC )2 4I y2C xC
2
1995 ,2 427 1
Iu
( 1995 ,2 427 )2 4 ( 246 )2 2032 ,9см4
2
2
1995 ,2 427 1
I
( 1995 ,2 427 )2 4 ( 246 )2 389 ,3см4
2
2
32.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙПроверка
I xC I y C I u I
1995,2+427=2032,9+389,3
2422,2=2422,2
I u
I xC I y C
2
1995 ,2 427
sin 2 I xC yC cos 2
0,299 246 0,954 0
2
234,4-234,6=0
33.
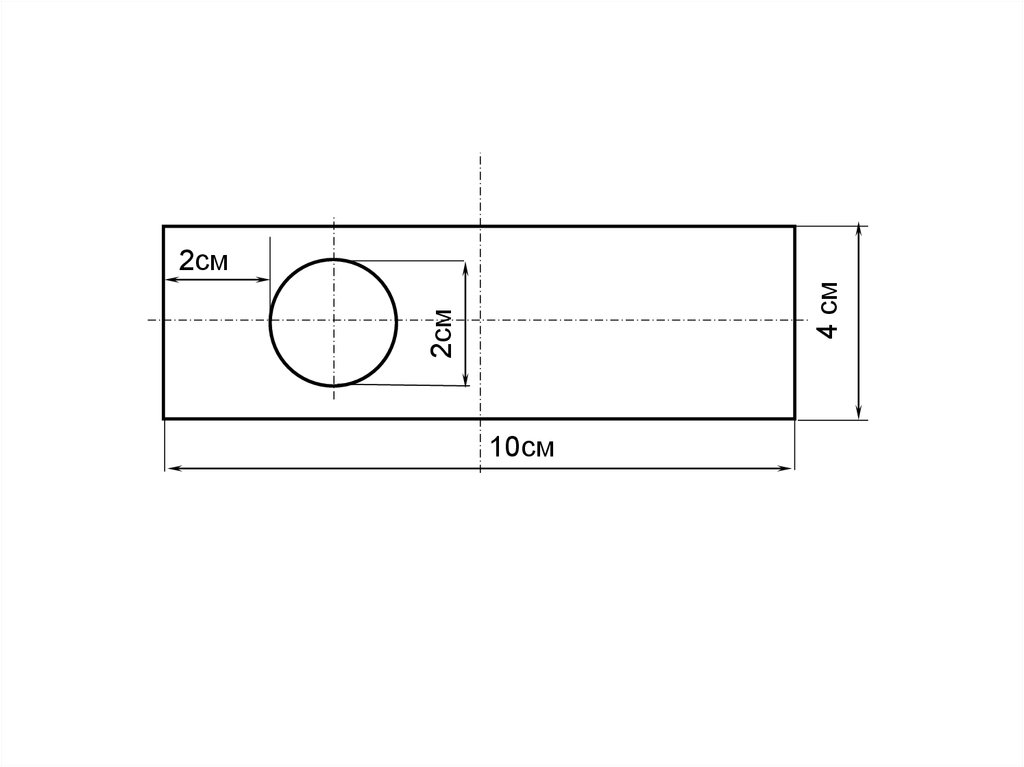
2см4 см
2см
10см
























 mathematics
mathematics








