Ранг матрицы (Rank of a matrix)

1. Лекция 6 Ранг матрицы

2. Ранг матрицы (Rank of a matrix)

Рассмотрим прямоугольную матрицу А
размерности m x n вида:
а11 а12
а21 а22
A
... ...
a а
m1 m 2
... а1n
... а2 n
... ...
... аmn
Выделим в матрице А k
строк и k столбцов, причем
1 k min m, n
Из элементов, стоящих на
пересечении выделенных
строк и столбцов, составим
определитель k-ого
порядка.
Определители, построение которых описано
выше,называются минорами k-ого порядка.

3.

Примеры миноров:
- первого порядка
M
(1)
1
а11 , M
(2)
1
а23
- второго порядка
M
(1)
2
а12 а1n
а21 а22
(2)
; M2
а32 а3n
аm1 аm 2
П. Выписать всевозможные миноры матрицы
1 2 0
A
.
3 4 1

4.

- первого порядка:
M
(1)
1
а11 1, M
(2)
1
а12 2,.... M
(6)
1
а23 1;
- второго порядка:
M
(1)
2
1 2
1 0
2 0
(2)
(3)
; M2
; M2
.
3 4
3 1
4 1
Упр. Выписать и вычислить всевозможные
миноры матрицы
1 2 3
B 4 0 5
6 7 8

5.

Опр. Рангом матрицы А называется наивысший
порядок отличного от нуля минора этой матрицы.
Обозначение ранга матрицы А: r(A); Rg(A)
0 r ( A) min m, n
Опр. Минор, порядок которого определяет ранг
матрицы называется базисным. Его столбцы и
строки, называются базисными столбцами и
базисными строками.

6.

П. Найти базисные миноры и указать ранг
матрицы:
2 0 4 0
А 3 0 6 0
1 0 3 0
Решение:
1 r ( A) min{m, n};
1 r ( A) 3.
Все миноры третьего порядка равны нулю!

7.

2 0 0
2 0 4
0 4 0
3 0 0 0; 3 0 6 0; 0 6 0 0.
1 0 0
1 0 3
0 3 0
Имеются миноры второго порядка не равные нулю:
2 4
(*)
10 0;
1 3
3 6
(**)
15 0.
1 3
Ранг матрицы А: r(A)=2;
Базисные миноры: (*), (**).

8. Линейная (не)зависимость строк матрицы

Будем рассматривать строки матрицы
А1 (a11a12 ...a1n ), А2 (a21a22 ...a2 n ),...,
Аm ( am1am 2 ...amn )
Опр. Линейной комбинацией (linear combination)
(ЛК) строк матрицы А c коэффициентами αi
называется выражение
1 А1 2 А2 ... k Аk ,
i R, i 1, k .

9.

Опр. Строки матрицы А называются линейно
зависимыми (linear dependent) (ЛЗ), если
2
i i 1, m; i 0 :
i 1
1 А1 2 А2 ... m Аm (0,0,...,0)
m
Опр. Строки матрицы А называются линейно
независимыми (linear independent) (ЛНЗ), если
i Аi (0,0,...,0) i 0 i 1, m
i 1
m

10.

П. Строки матрицы А
линейно зависимы!
1
1
А
1
0
6
2
0
1
8
4
4
4
7
5
1
2
Составим линейную комбинацию строк
матрицы с коэффициентами 0, -1, 1, 2:
1 А1 2 А2 ... k Аk 0 (1,6,8,7)
( 1) ( 1,2,4,5) 1 ( 1,0, 4,1)
2 (0,1,4,2) (0,0,0,0) (1, 2, 4, 5)
( 1,0, 4,1) (0,2,8,4) (0,0,0,0).

11.

Т. Если строки матрицы ЛЗ, то хотя бы одна
строка матрицы является ЛК остальных
строк. Верно и обратное.
►1. Если строки матрицы ЛЗ, то
m
2
i i 1, m; i 0 :
i 1
1 А1 2 А2 ... m Аm (0,0,...,0).
Пусть для определенности α1≠0, тогда
1 А1 2 А2 ... m Аm ;
2
m
А1 А2 ...
Аm .
1
1

12. Теорема о базисном миноре

Базисные строки (столбцы) матрицы A,
соответствующие любому ее базисному минору M,
линейно независимы.
Любые строки (столбцы) матрицы A, не входящие в
М, являются линейными комбинациями базисных
строк (столбцов).

13.

Методы вычисления ранга матрицы
1. Метод окаймляющих миноров
(ознакомительно на самост. работу)
Т. Если в матрице какой-нибудь минор порядка k не
равен нулю, а все миноры порядка k+1, его
содержащие, равны нулю, то ранг матрицы равен k.
П. Найти ранг матрицы методом окаймляющих
миноров:

14.

Решение. Фиксируем отличный от нуля минор
второго порядка:
Составим окаймляющие миноры третьего порядка:
Вывод: Rg(A)=2.

15.

2. Метод элементарных преобразований
Т. Ранг матрицы не изменяется при следующих
элементарных преобразованиях:
1. Rg A Rg A ;
Т
a11 ... a1n
ka11 ... ka1n
2. Rg ... ... ... Rg ... ... ... ,
a
a
...
a
...
a
mn
mn
m1
m1
k R \{0};

16.

a11 ... a1n
ak1 ... akn
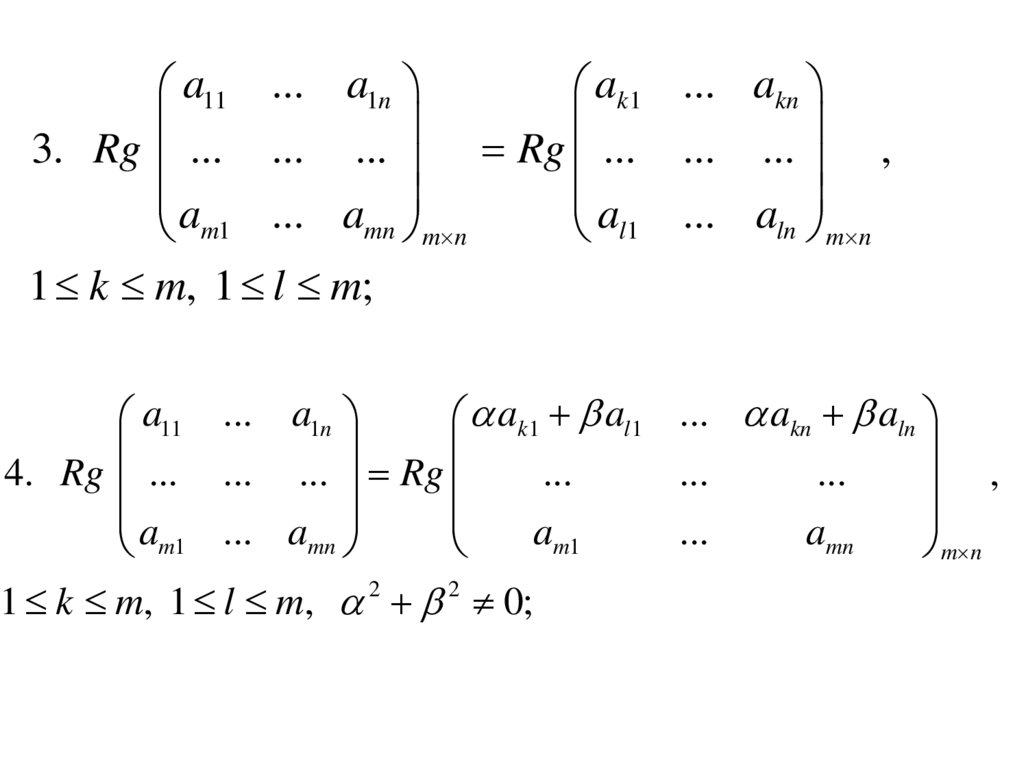
3. Rg ... ... ... Rg ... ... ... ,
a
a ... a
...
a
mn m n
ln m n
m1
l1
1 k m, 1 l m;
a11 ... a1n
ak 1 al1 ... akn aln
4. Rg ... ... ... Rg
...
...
...
,
a
...
a
a
...
a
mn
m1
mn
m1
m n
1 k m, 1 l m, 2 2 0;

17.

0 ..0.. 0
a21 ... a2 n
5. Rg ...
...
... Rg ... ... ...
,
a
a
...
a
...
a
mn m n
mn ( m 1) n
m1
m1
6. если удалить из А столбец (строку), который
является линейной комбинацией других столбцов
(строк).
Упр. Доказать свойства 1-6. Указание:
воспользоваться соответствующими свойствами
определителей.

18.

С помощью элементарных преобразований можно
привести прямоугольную матрицу к ступенчатому
виду
a11 a12
0
a
22
А 0 0
... ...
0 0
где
...
...
...
...
...
a11 , a22 ,..., arr 0.
a1r
a2 r
a3r
...
arr
a1r 1
a2 r 1
a3r 1
...
arr 1
...
...
...
...
...
a1n
a2 n
a3n
...
arn

19.

Т. Ранг ступенчатой матрицы равен числу r ее
ненулевых строк.
Доказательство
r ( A) r.
a11 a12
0 a22
... ...
0
0
... a1r
... a2 r
a11 a22 ... arr 0
... ...
... arr
r(A)=r, что и т.д.

20.

П. Вычислить ранг матрицы методом
элементарных преобразований:
Решение:
1 3 2
A 0 5 4
1 7 6
1 3 2 (3) (1) 1 3 2
A 0 5 4 ~ 0 5 4
1 7 6
0 10 8
1 3 2
r ( A) 2.
0 5 4
(3) 2 (2)
~
1 3 2
0 5 4
0 0 0

21.

П. Вычислить ранг матрицы A методом
элементарных преобразований:
r A 2.

22.

Упр. Вычислить ранг матрицы A методом элементарных
преобразований: