Презентация по геометрии на тему _ Предмет стереометрии. Аксиомы стереометрии_ (10 класс)

1. Стереометрия Аксиомы стереометрии

Геометрия 10 класс.

2.

- Что такое геометрия?
Геометрия – наука о свойствах геометрических фигур
«Геометрия» - (греч.) – «землемерие»
- Что такое планиметрия?
Планиметрия – раздел геометрии, в котором изучаются
свойства фигур на плоскости.
- Основные понятия планиметрии?
Основные понятия планиметрии:
А
точка
а
прямая

3.

Для обозначения точек как и в планиметрии
используют прописные латинские буквы:
F
Прямую обозначают одной строчной
латинской буквой и двумя прописными
латинскими буквами:
l
A
B

4. Основные аксиомы планиметрии.

В
С
D
b
А
Какова бы ни была
прямая, существуют
точки, принадлежащие
этой прямой, и точки, не
принадлежащие ей.
Через любые две
точки можно провести
прямую, и только
одну.

5.

Стереометрия изучает свойства фигур в
пространстве.
Слово «стереометрия» происходит от
греческих слов «стереос» объемный,
пространственный, «метрео» – мерить.
Основные фигуры: точка, прямая,
плоскость.

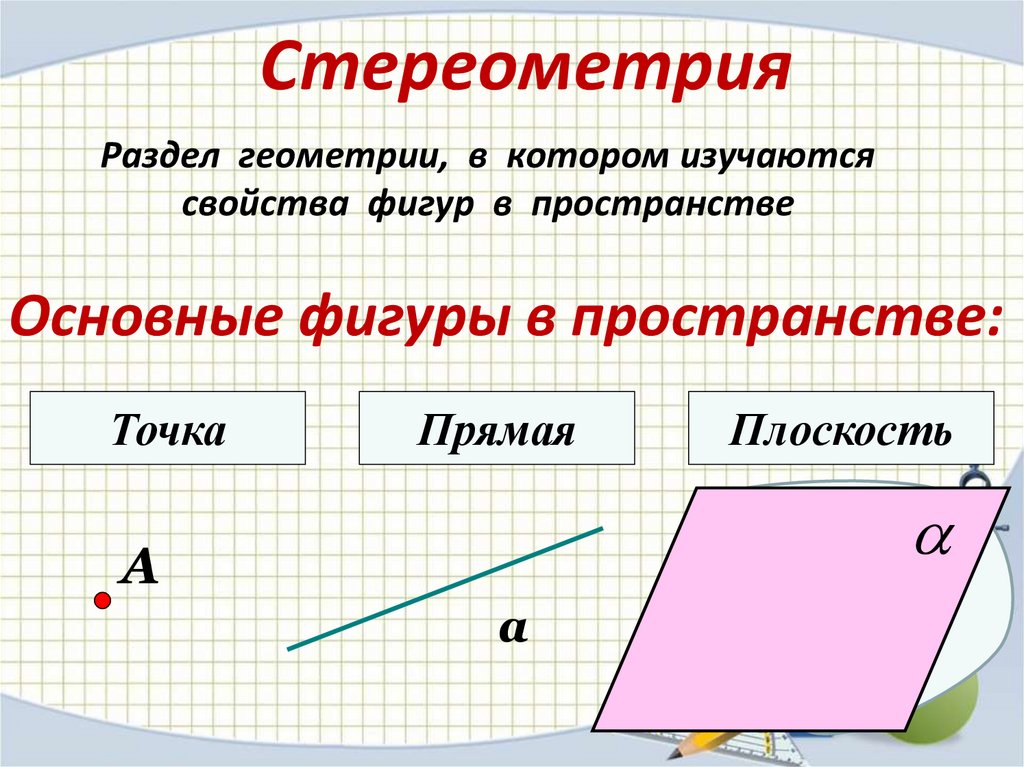
6. Стереометрия

Раздел геометрии, в котором изучаются
свойства фигур в пространстве
Основные фигуры в пространстве:
Точка
Прямая
Плоскость
А
а

7.

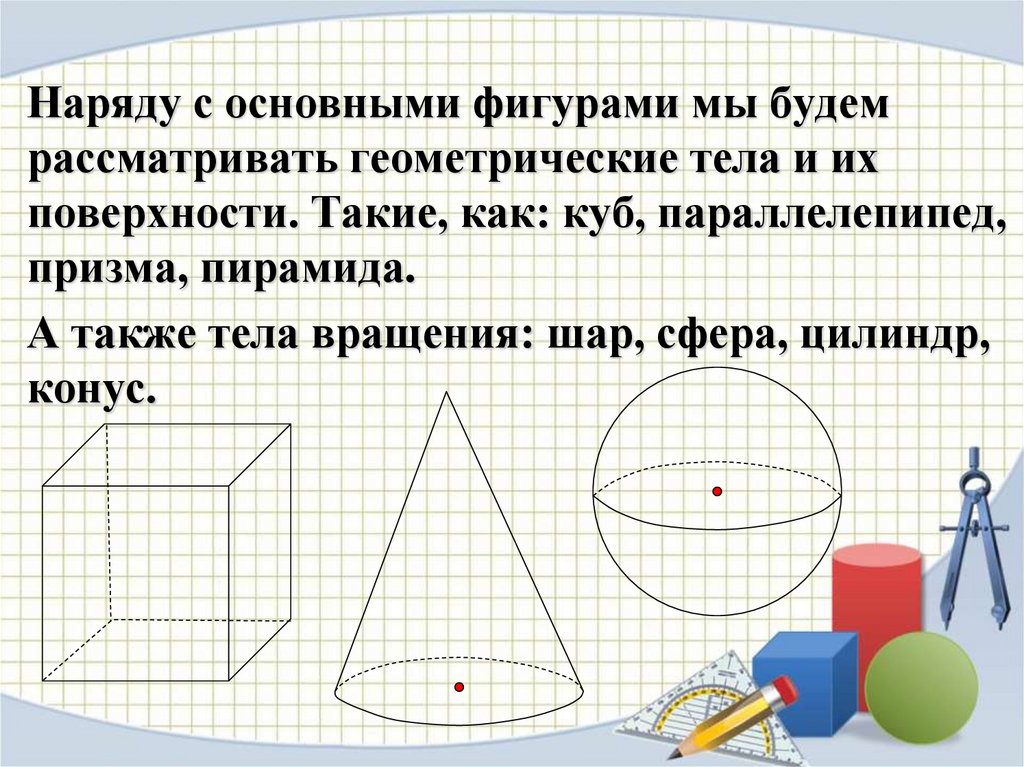
Наряду с основными фигурами мы будем
рассматривать геометрические тела и их
поверхности. Такие, как: куб, параллелепипед,
призма, пирамида.
А также тела вращения: шар, сфера, цилиндр,
конус.

8.

Плоскость в стереометрии обозначают греческими
буквами, например:
А на рисунках чаще всего плоскость изображают в
виде параллелограмма. Но следует понимать и
представлять себе данную геометрическую фигуру
как неограниченную во все стороны.

9.

При изучении в курсе стереометрии геометрических
тел пользуются их плоскими изображениями на
чертеже.
Изображением пространственной фигуры служит ее
проекция на плоскость.
Изображения конуса

10.

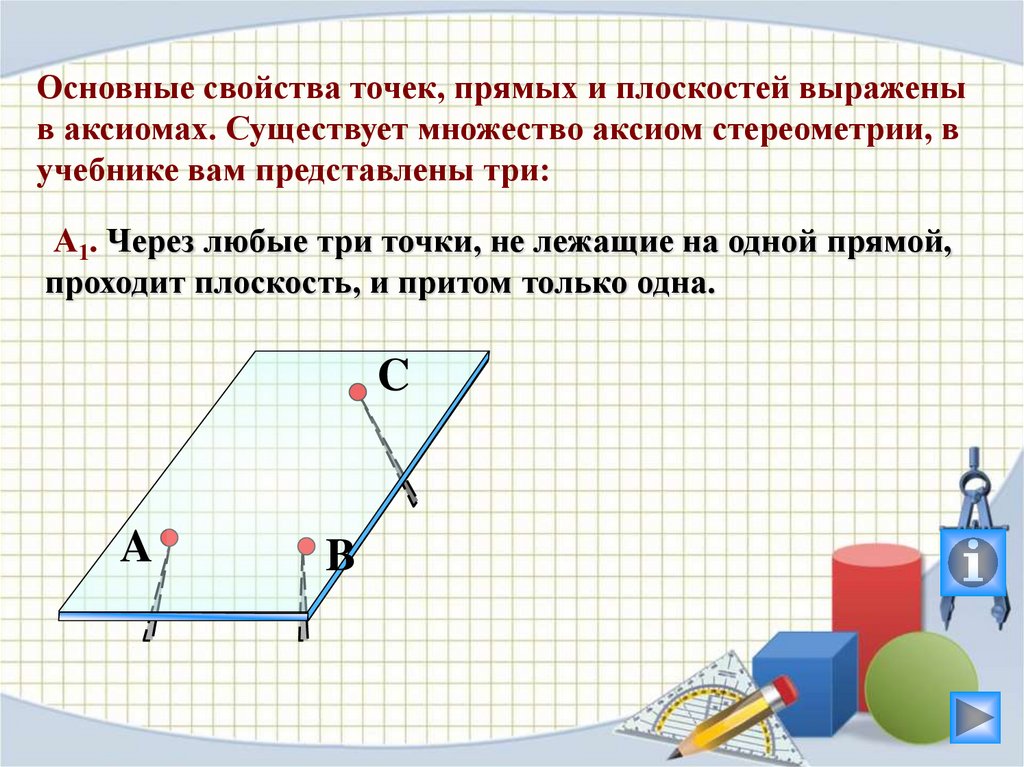
Основные свойства точек, прямых и плоскостей выражены
в аксиомах. Существует множество аксиом стереометрии, в
учебнике вам представлены три:
А1. Через любые три точки, не лежащие на одной прямой,
проходит плоскость, и притом только одна.
C
A
B

11.

Самый простой пример к аксиоме А1 из повседневной
жизни:
Табурет с тремя ножками всегда идеально
встанет на пол и не будет качаться. У
табурета с четырьмя ножками бывают
проблемы с устойчивостью, если ножки стула
не одинаковые по длине.
Табурет качается, т. е. опирается на три
ножки, а четвертая ножка (четвертая
«точка») не лежит в плоскости
пола, а висит в воздухе.

12.

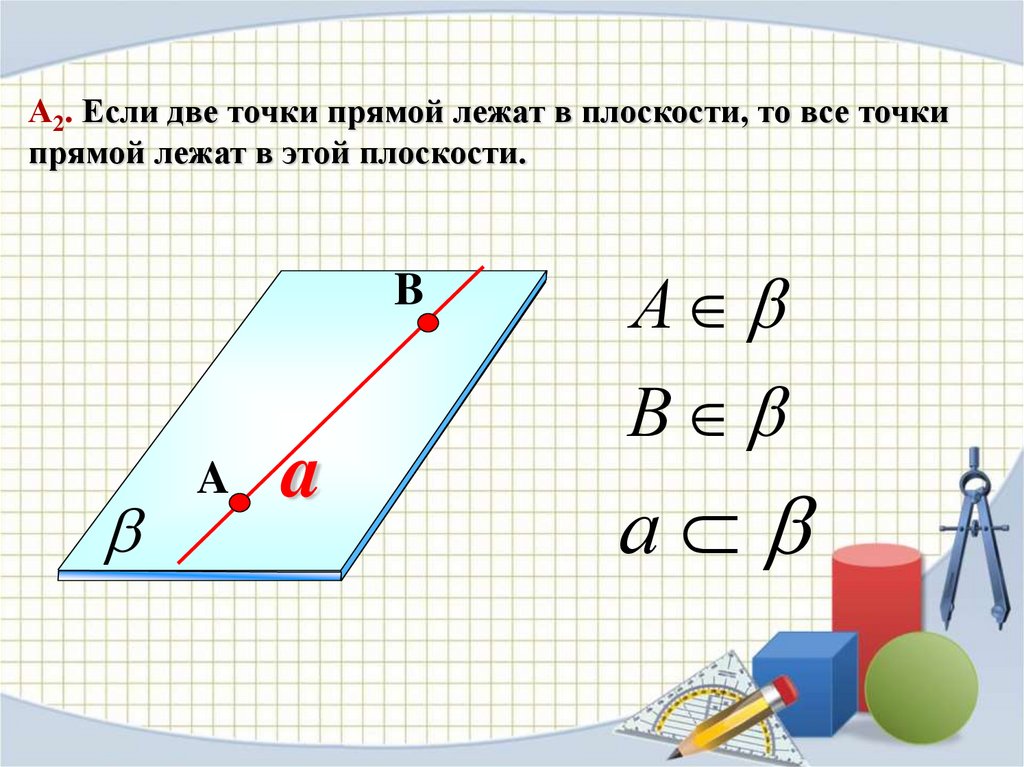
А2. Если две точки прямой лежат в плоскости, то все точки
прямой лежат в этой плоскости.
B
A
a
А
В
а

13.

Свойство, выраженное в аксиоме А2, используется
для проверки «ровности» чертежной линейки.
Линейку прикладывают краем к плоской
поверхности стола. Если край линейки ровный, то
он всеми своими точками прилегает к поверхности
стола.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
IIIIIIIIIIIIIIIIIIIIIIIIII
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Если край неровный, то в каких-то местах между
ним и поверхностью стола образуется просвет.

14.

Следствия из аксиомы А2:
1. Если прямая не лежит в данной плоскости, то она имеет с
ней не более одной общей точки.
2. Если прямая и плоскость имеют только одну общую
точку, то говорят, что они пересекаются.
a
N
а N

15.

А3. Если две плоскости имеют общую точку, то они имеют
общую прямую, на которой лежат все общие точки этих
плоскостей.
Самый простой пример к
аксиоме А3 из
повседневной жизни
является пересечение
двух смежных стен
комнаты.
a
a

16.

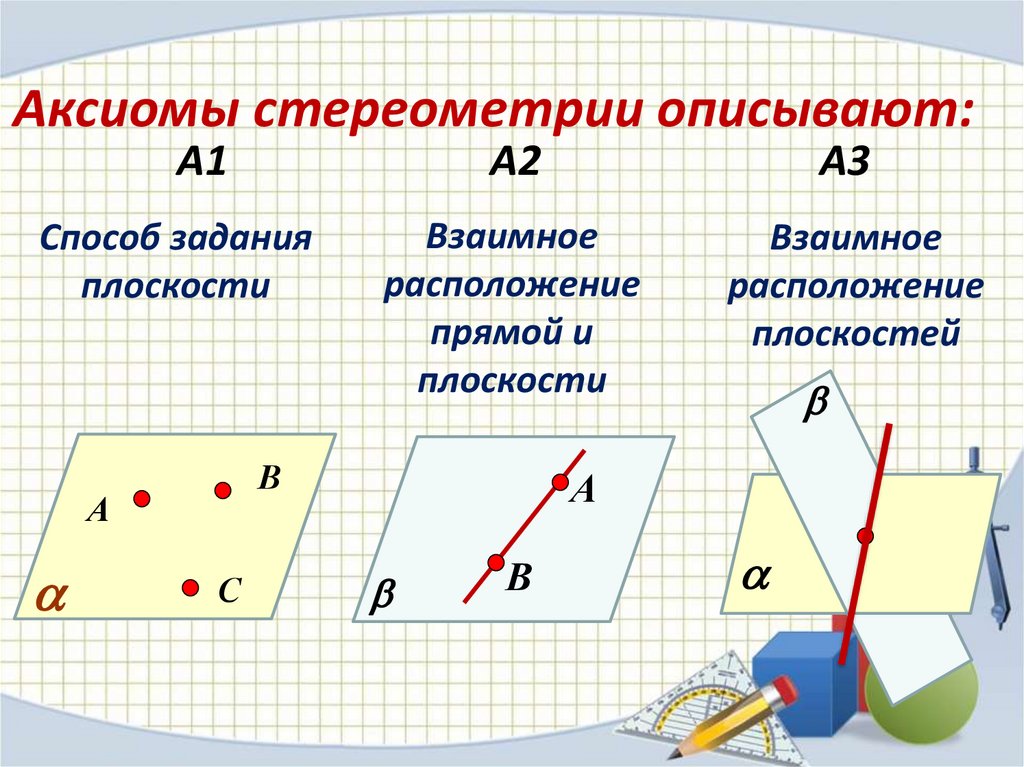
Аксиомы стереометрии описывают:
А1
А2
А3
Способ задания
плоскости
Взаимное
расположение
прямой и
плоскости
Взаимное
расположение
плоскостей
В
А
С
А
В

17.

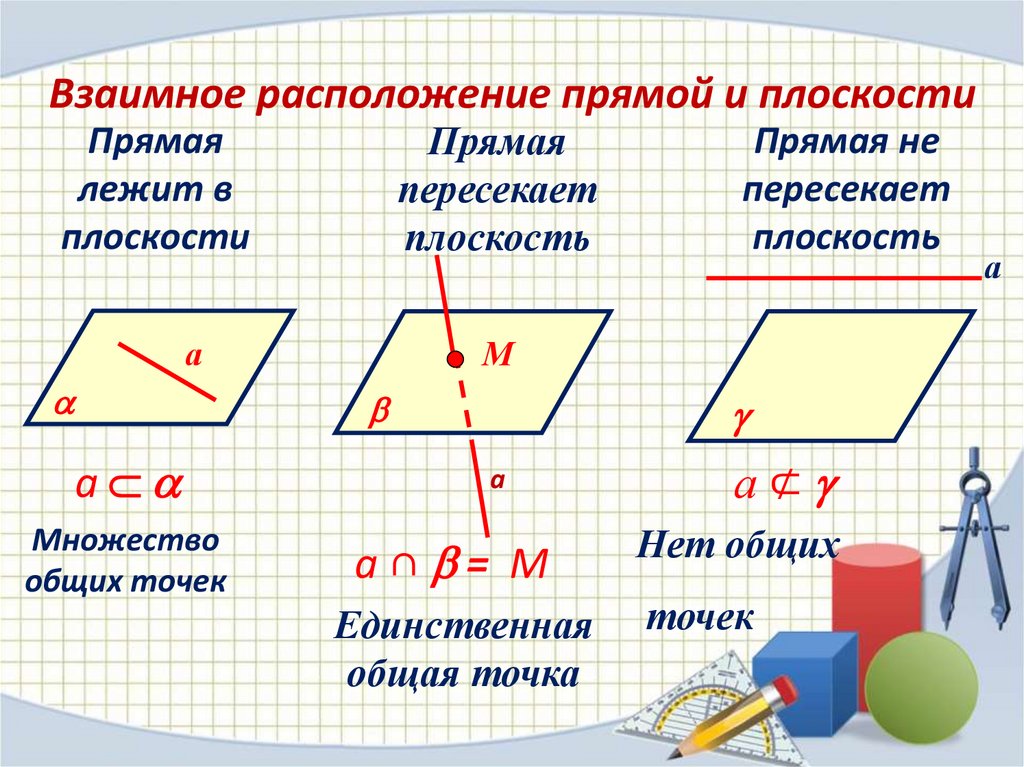
Взаимное расположение прямой и плоскости
Прямая
пересекает
плоскость
Прямая
лежит в
плоскости
а
М
а
Множество
общих точек
Прямая не
пересекает
плоскость
а
а⊄
а∩ = М
Нет общих
Единственная
общая точка
точек
а

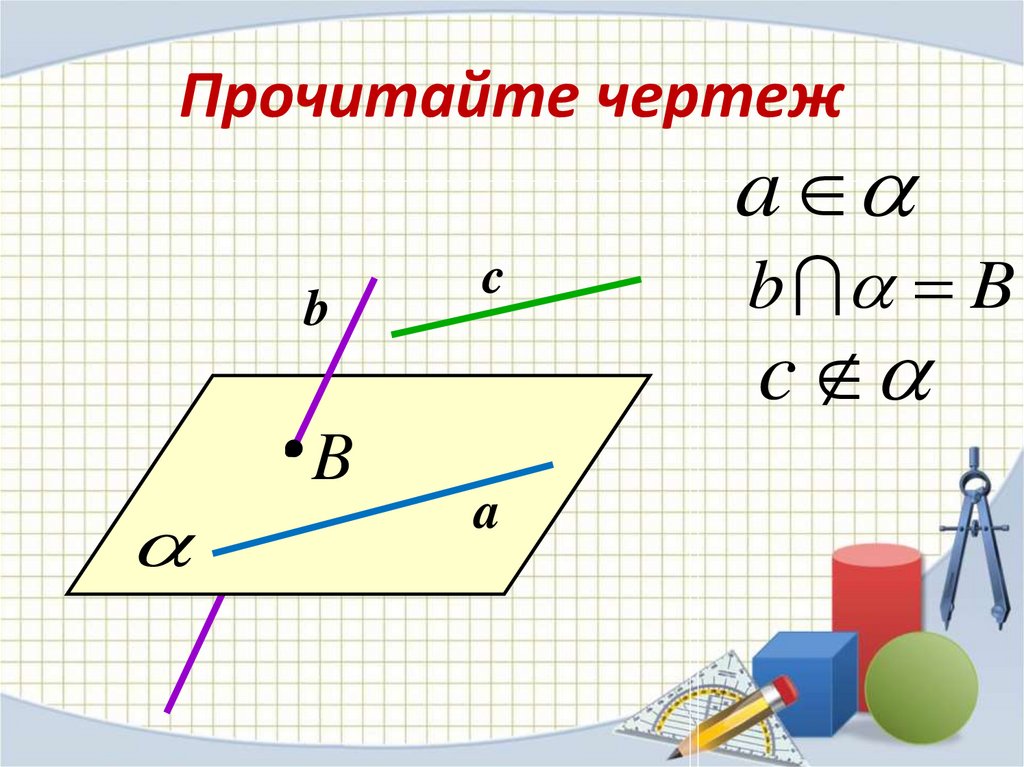
18. Прочитайте чертеж

a
b
B
c
b B
c
a

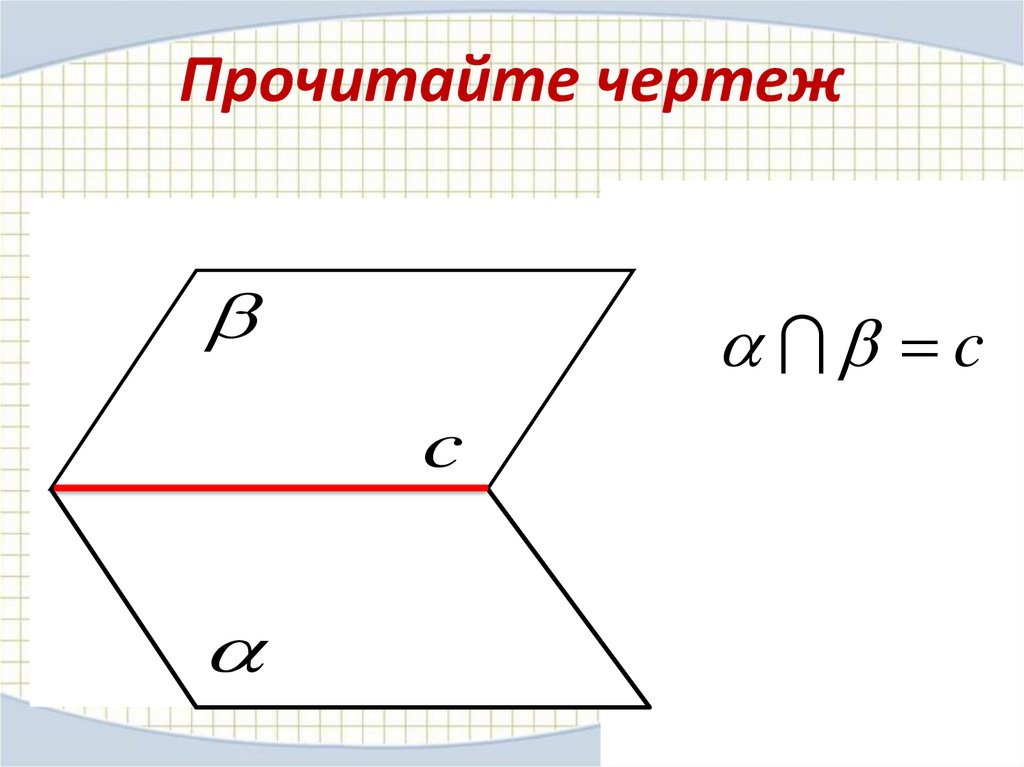
19. Прочитайте чертеж

c
c

20.

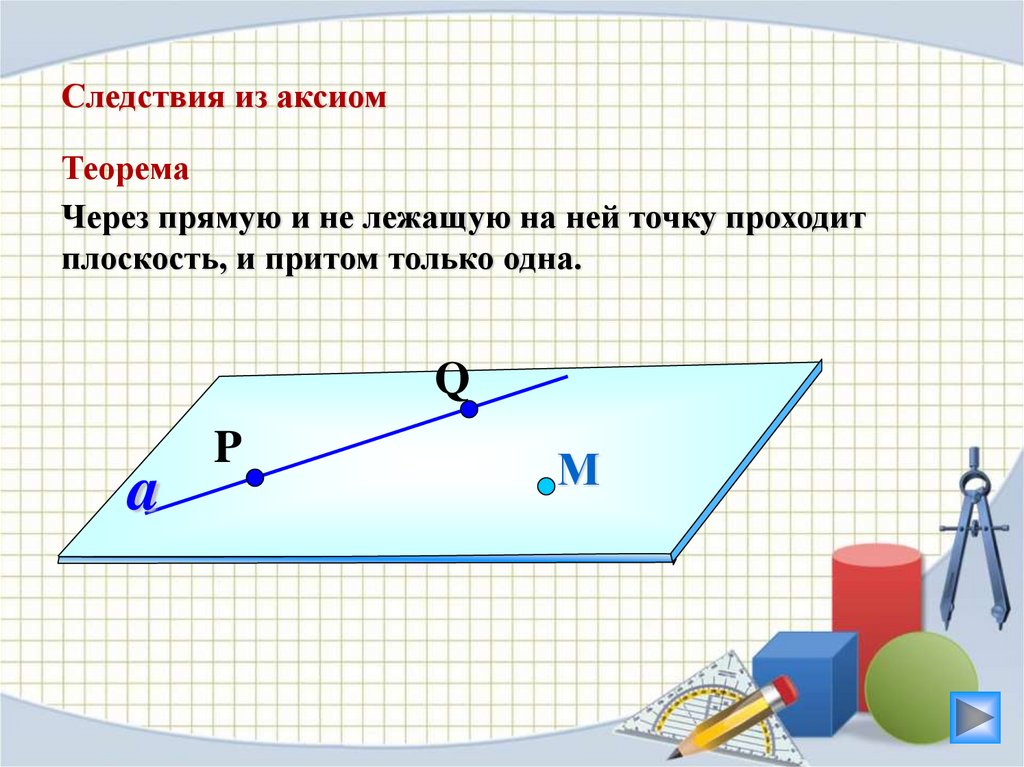
Следствия из аксиом
Теорема
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна.
Q
a
P
М

21.

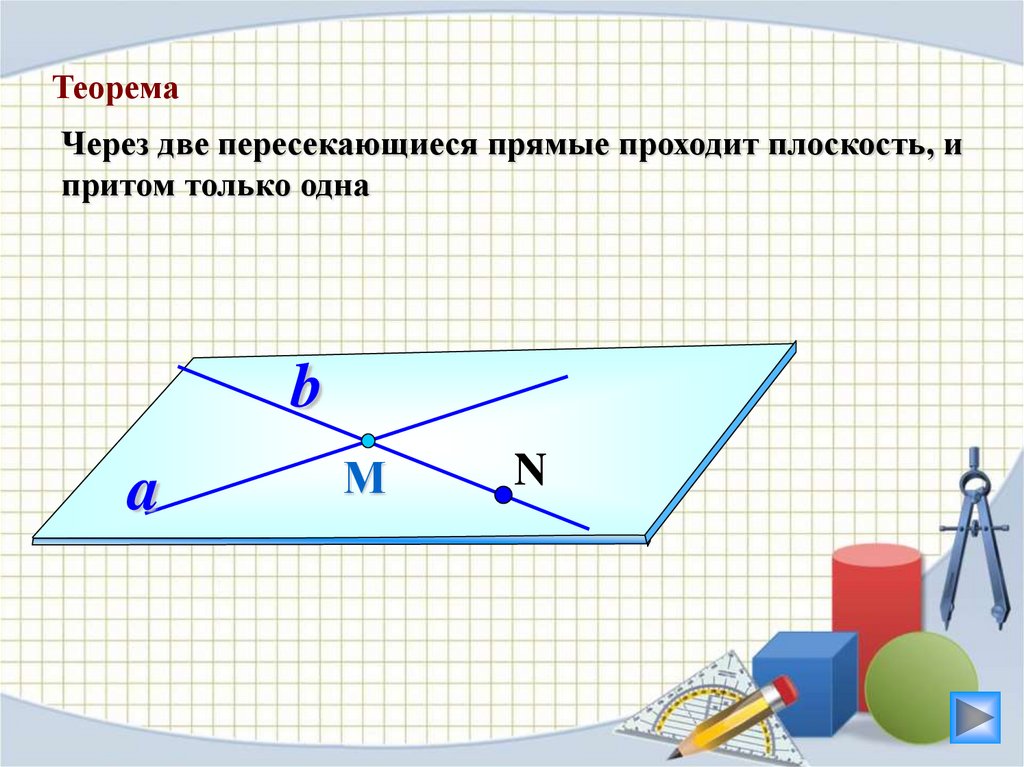
Теорема
Через две пересекающиеся прямые проходит плоскость, и
притом только одна
b
a
М
N