Аксиомы стереометрии. 10 класс

1.

Аксиомы
стереометрии

2.

Планиметрия
Стереометрия
Изучает свойства
геометрических фигур на
плоскости
Изучает свойства фигур в
пространстве
В переводе с греческого
слово «геометрия» означает
«землемерие»
«гео» – по-гречески земля,
«метрео» – мерить
Слово «стереометрия»
происходит от греческих слов
«стереос» объемный,
пространственный, «метрео» –
мерить

3.

Планиметрия
Стереометрия
Основные фигуры: точка,
прямая
Основные фигуры: точка,
прямая, плоскость
Другие фигуры: отрезок, луч,
треугольник, квадрат, ромб,
параллелограмм, трапеция,
прямоугольник, выпуклые и
невыпуклые n-угольники,
круг, окружность, дуга и др.
Наряду с этими фигурами мы
будем рассматривать
геометрические тела и их
поверхности.
Например, многогранники.
Куб, параллелепипед, призма,
пирамида.
Тела вращения.
Шар, сфера, цилиндр, конус.

4.

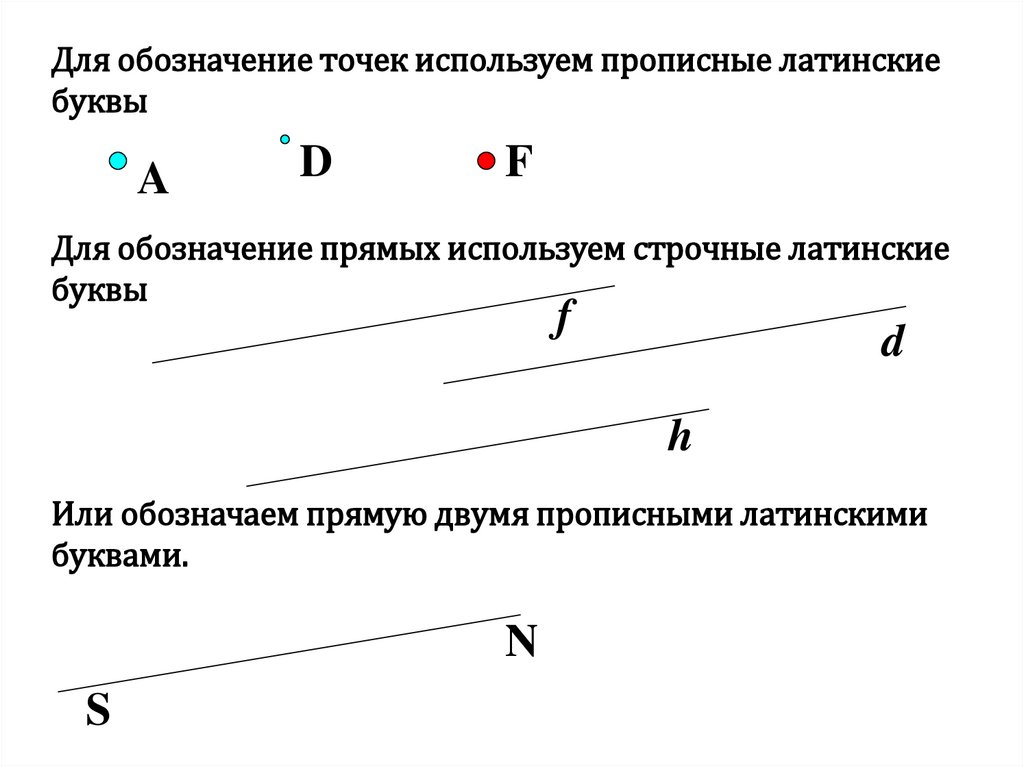
Для обозначение точек используем прописные латинские
буквы
A
D
F
Для обозначение прямых используем строчные латинские
буквы
f
d
h
Или обозначаем прямую двумя прописными латинскими
буквами.
N
S

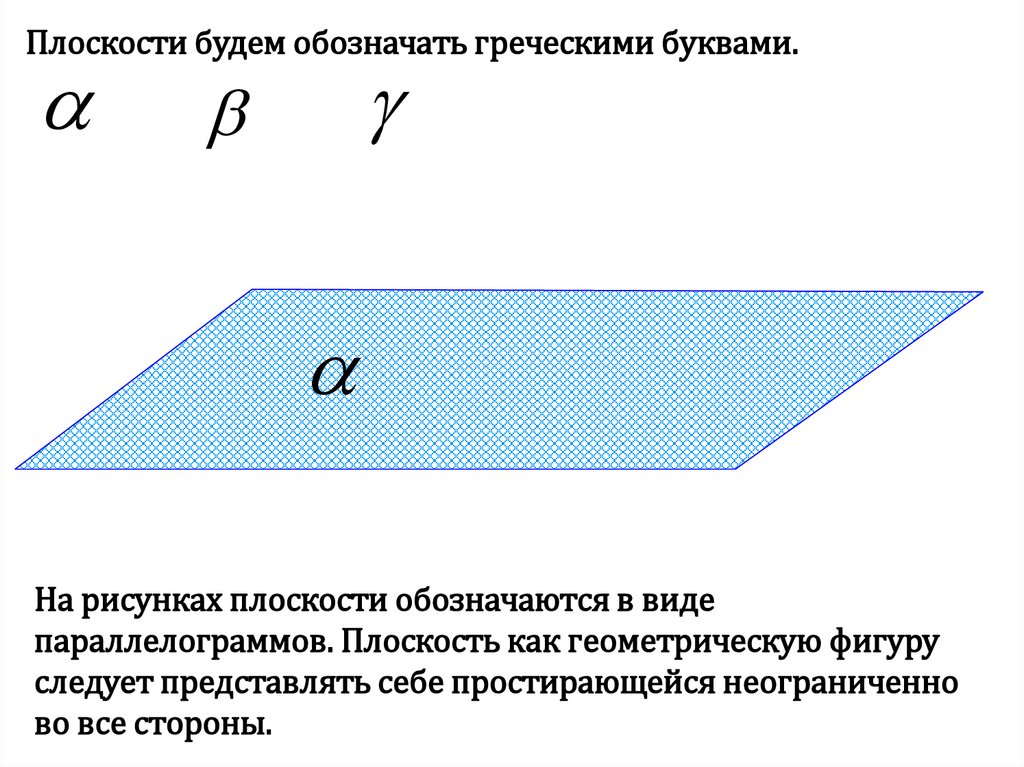
5.

Плоскости будем обозначать греческими буквами.
На рисунках плоскости обозначаются в виде
параллелограммов. Плоскость как геометрическую фигуру
следует представлять себе простирающейся неограниченно
во все стороны.

6.

D
C
C
A
B

7.

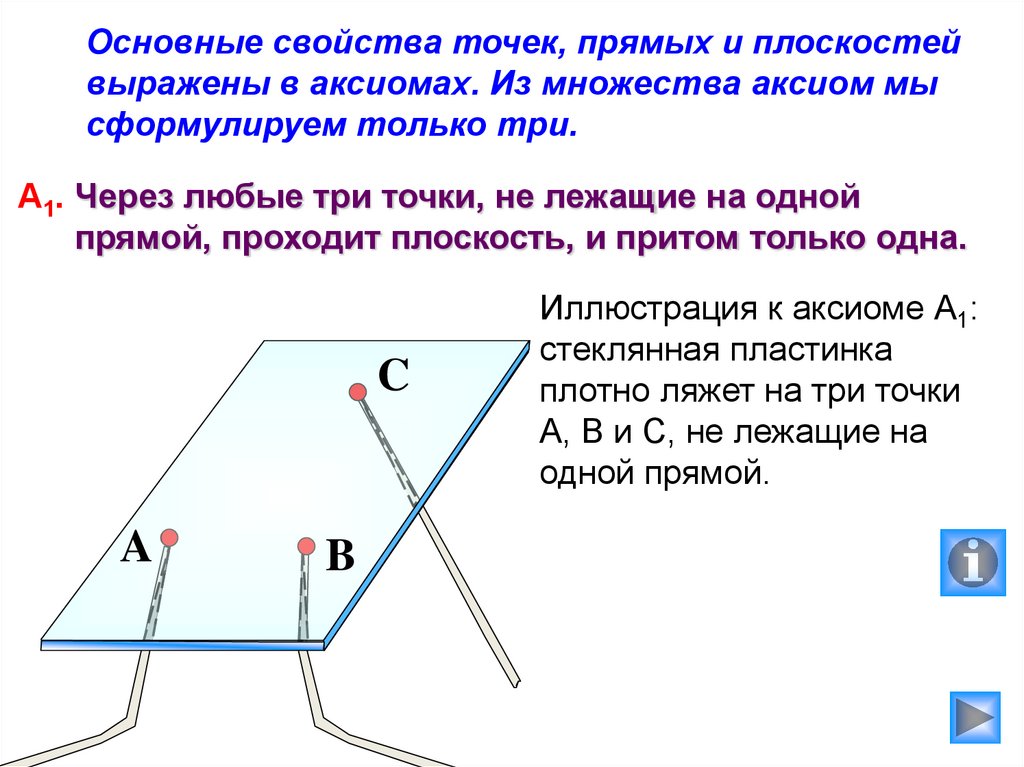
Основные свойства точек, прямых и плоскостей
выражены в аксиомах. Из множества аксиом мы
сформулируем только три.
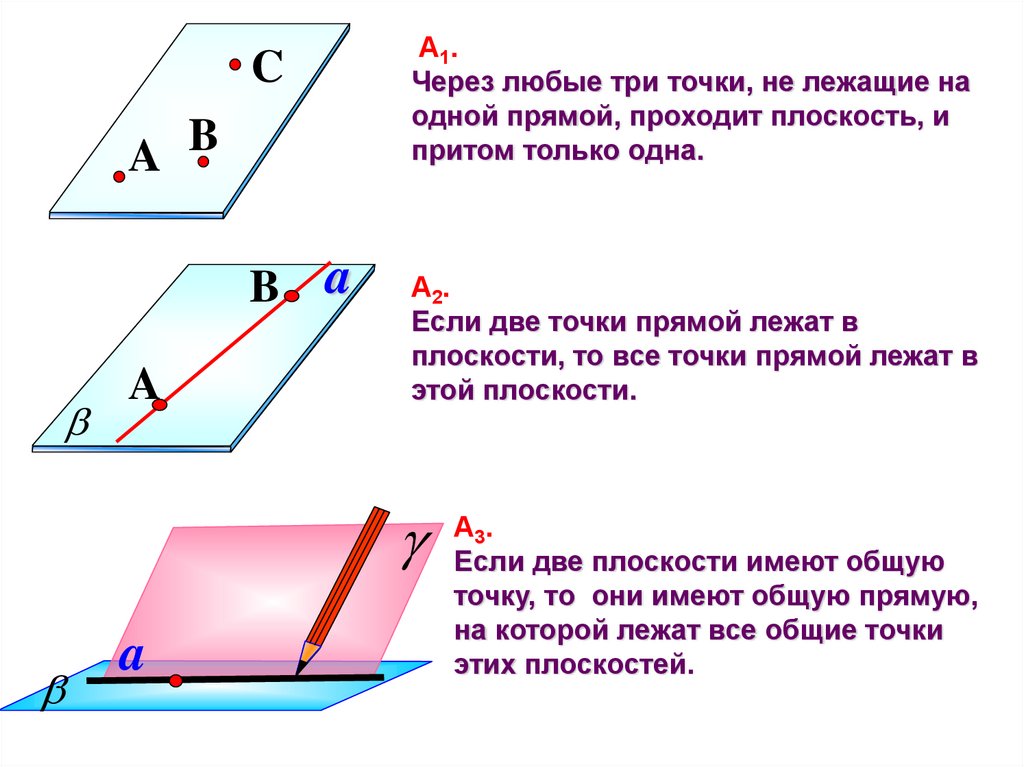
А1. Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна.
C
A
B
Иллюстрация к аксиоме А1:
стеклянная пластинка
плотно ляжет на три точки
А, В и С, не лежащие на
одной прямой.

8.

Иллюстрации к аксиоме А1 из жизни.
Для
видеокамеры,
фотосъемки
для других
приборов
часто
Табурет
с тремя ножками
всегдаиидеально
встанет
на пол
и
используют
штативУ–табурета
треногу. Три
ножки штатива
устойчиво
не будет качаться.
с четырьмя
ножками
бывают
расположатся
на любом полуесли
в помещениях,
проблемы с устойчивостью,
ножки стулана
неасфальте
одинаковые
или
прямоТабурет
на газоне
на улице,
наопирается
песке на пляже
в а
по длине.
качается,
т. е.
на триили
ножки,
траве
в лесу.
Три(четвертая
ножки штатива
всегда
четвертая
ножка
«точка»)
не найдут
лежит вплоскость.
плоскости
пола, а висит в воздухе.

9.

Построение прямых углов на местности с помощью
простейшего прибора,
который называется экер.
А
В
Треножник
с
экером.
1
О

10.

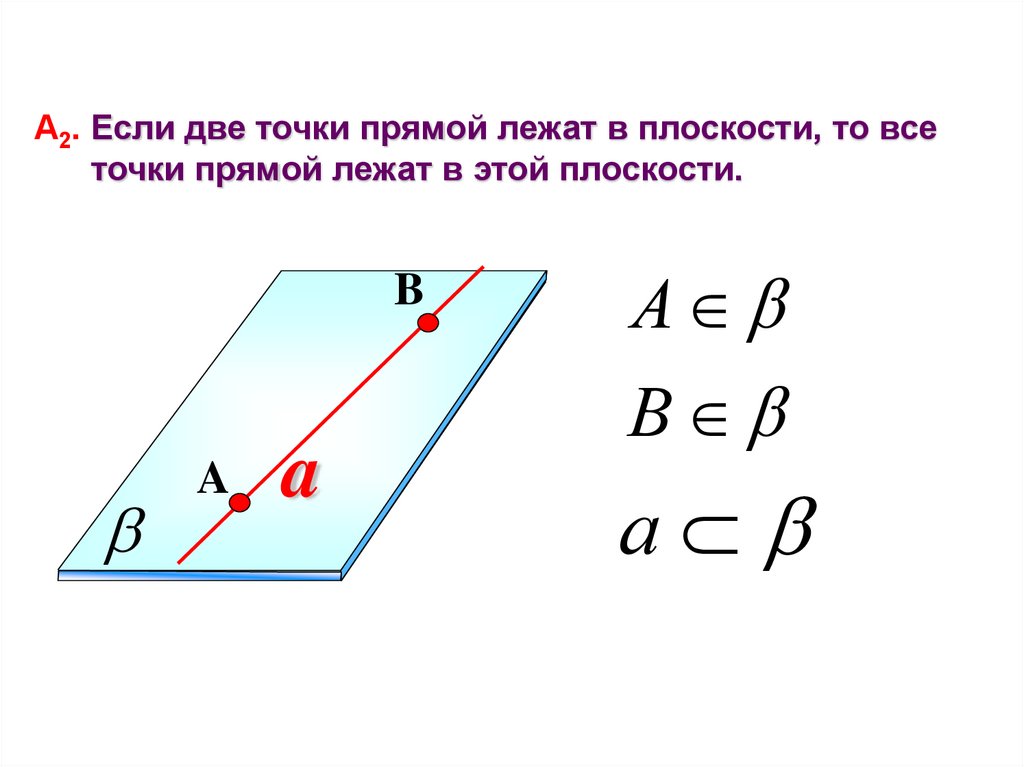
А2. Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости.
B
A
a
А
В
а

11.

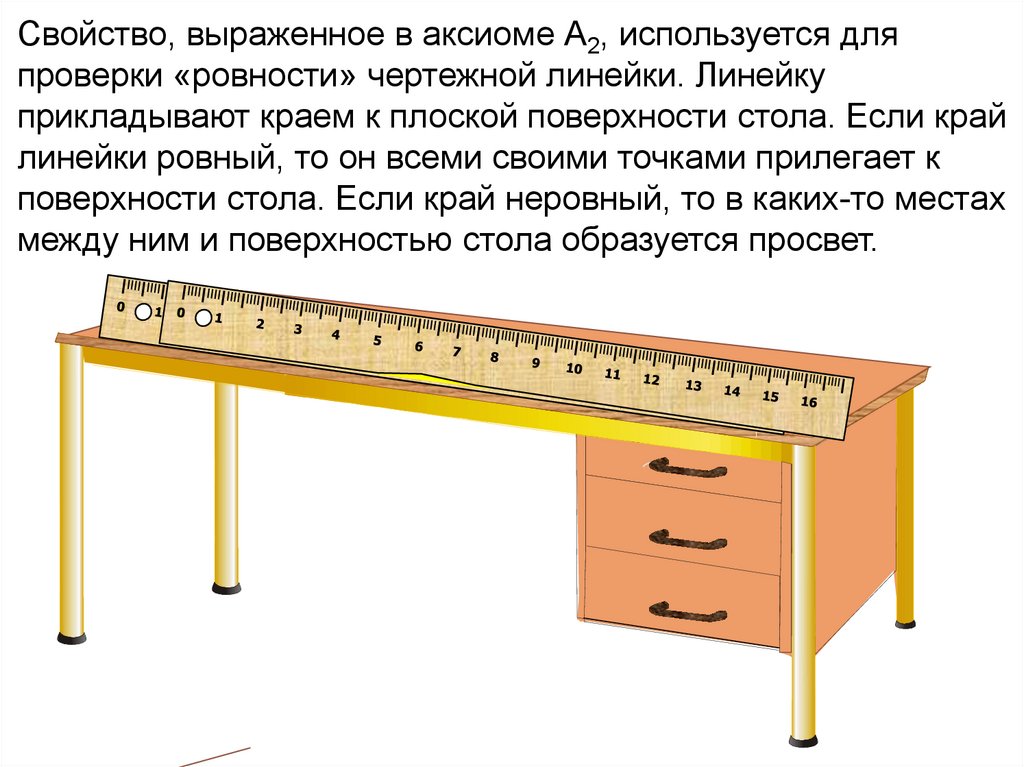
Свойство, выраженное в аксиоме А2, используется для
проверки «ровности» чертежной линейки. Линейку
прикладывают краем к плоской поверхности стола. Если край
линейки ровный, то он всеми своими точками прилегает к
поверхности стола. Если край неровный, то в каких-то местах
между ним и поверхностью стола образуется просвет.

12.

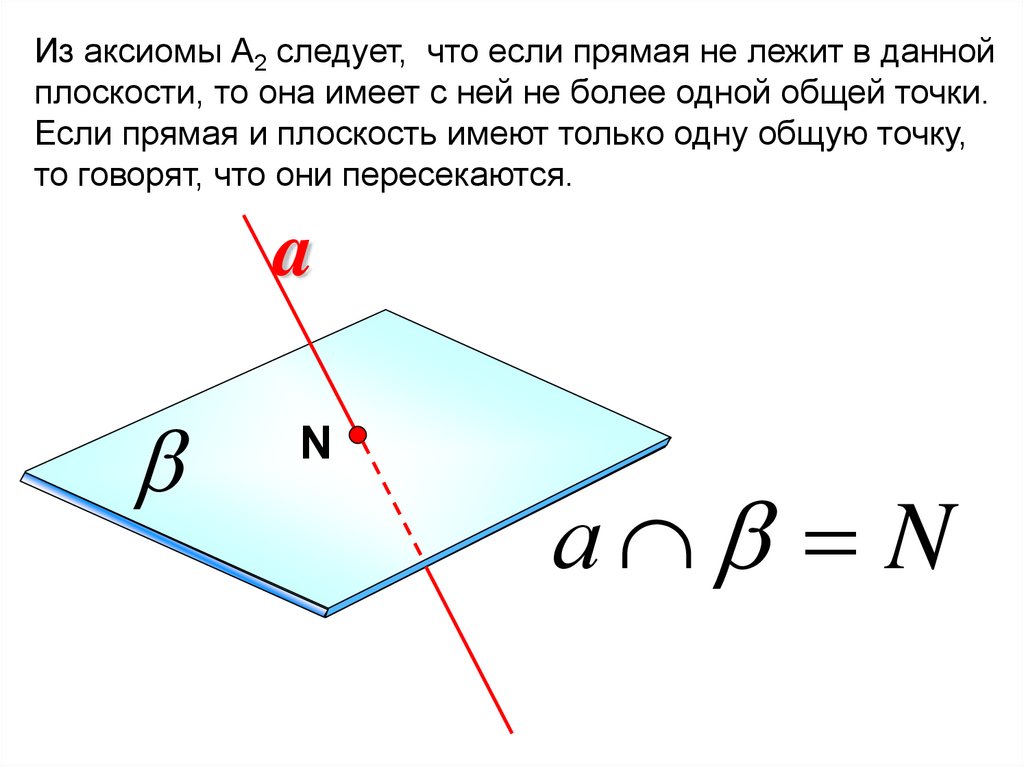
Из аксиомы А2 следует, что если прямая не лежит в данной
плоскости, то она имеет с ней не более одной общей точки.
Если прямая и плоскость имеют только одну общую точку,
то говорят, что они пересекаются.
a
N
а N

13.

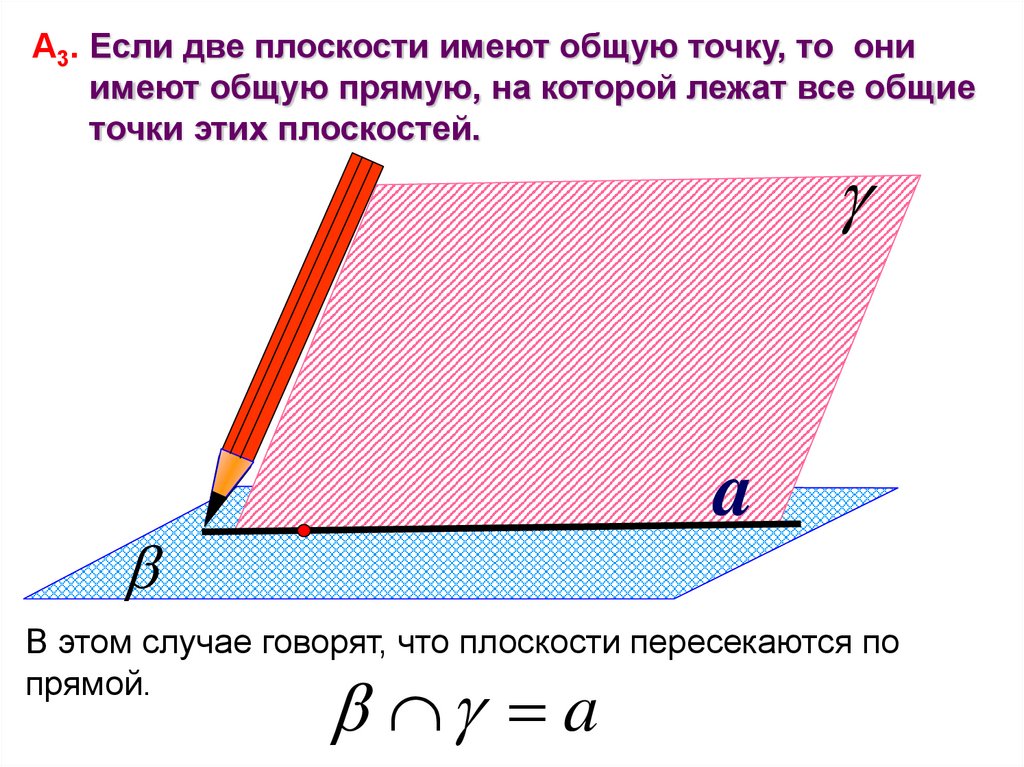
А3. Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
a
В этом случае говорят, что плоскости пересекаются по
прямой.
a

14.

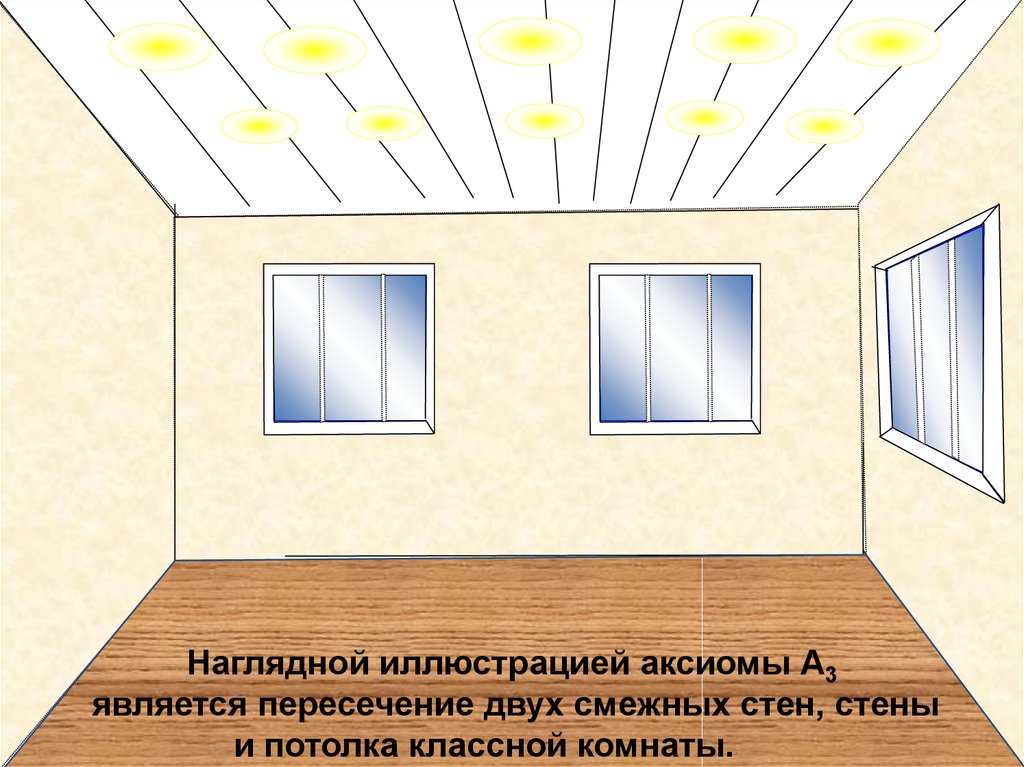
Наглядной иллюстрацией аксиомы А3
является пересечение двух смежных стен, стены
и потолка классной комнаты.

15.

C
B
A
B a
A
А 1.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
А 2.
Если две точки прямой лежат в
плоскости, то все точки прямой лежат в
этой плоскости.
a
А 3.
Если две плоскости имеют общую
точку, то они имеют общую прямую,
на которой лежат все общие точки
этих плоскостей.

16.

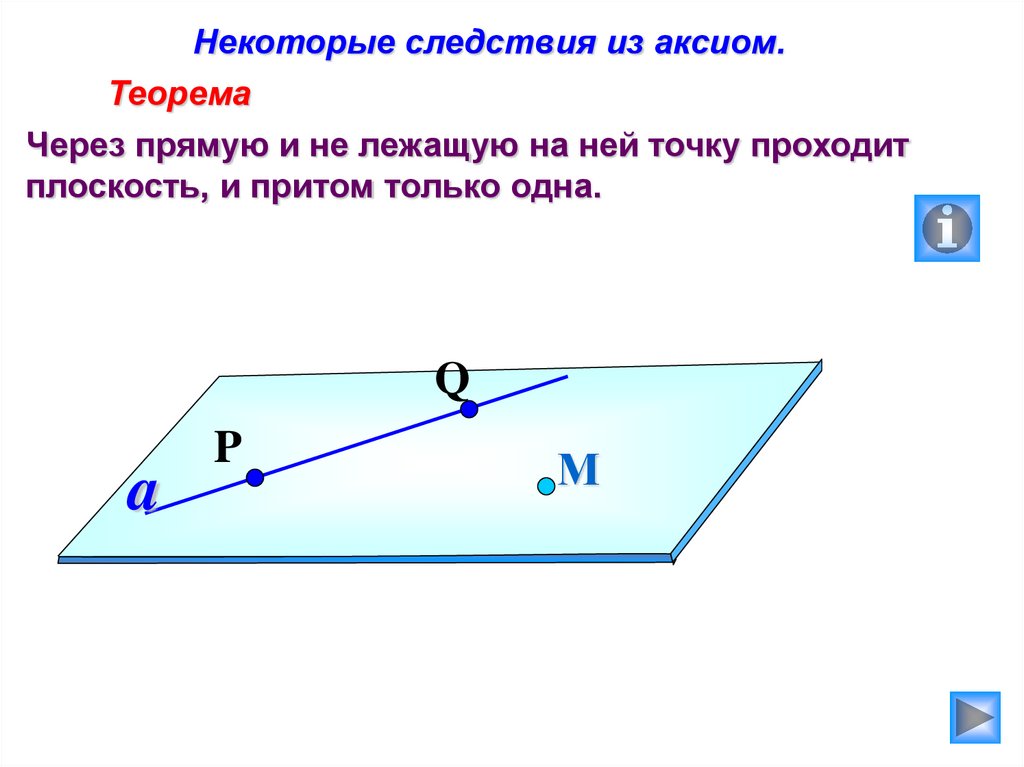
Некоторые следствия из аксиом.
Теорема
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна.
Q
a
P
М

17.

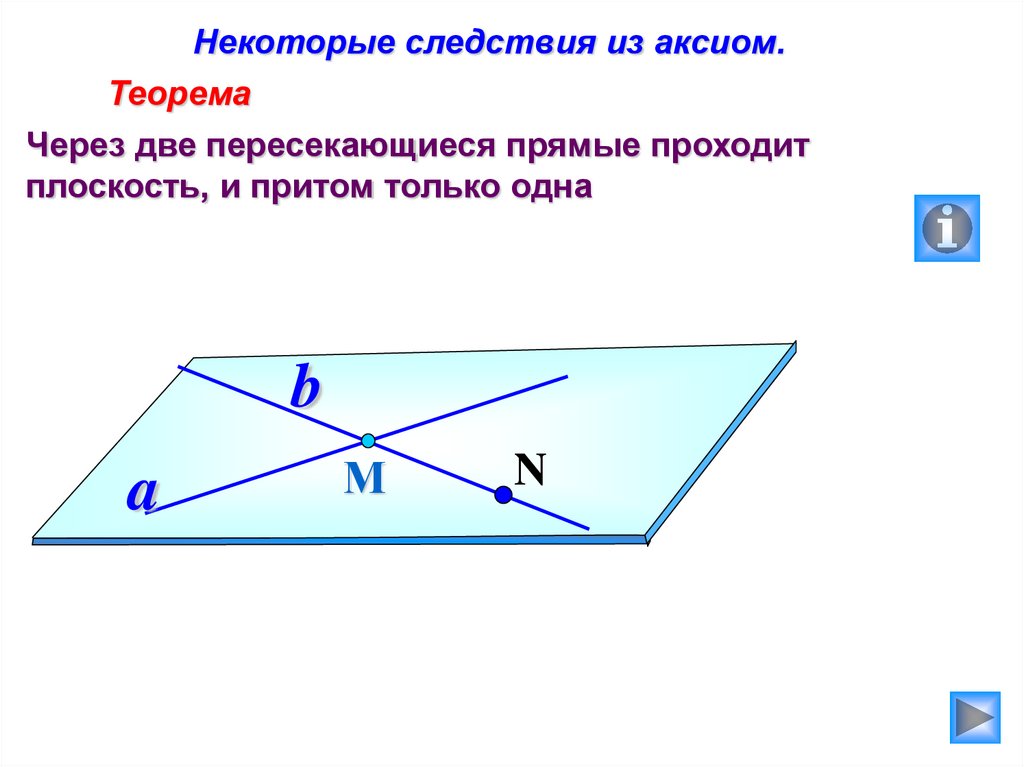
Некоторые следствия из аксиом.
Теорема
Через две пересекающиеся прямые проходит
плоскость, и притом только одна
b
a
М
N

18.

Следствия из аксиом
Теорема
Через две параллельные прямые
можно провести плоскость и притом
только одну.

19.

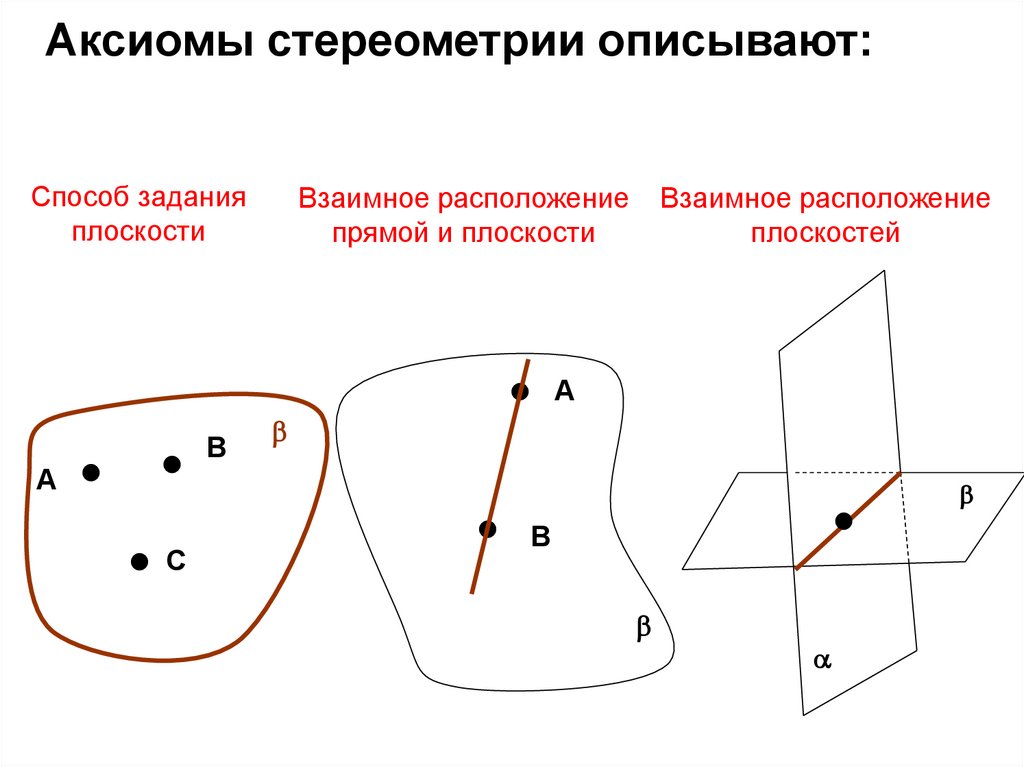
Аксиомы стереометрии описывают:
Способ задания
плоскости
Взаимное расположение
прямой и плоскости
Взаимное расположение
плоскостей
А
В
А
С
В

20.

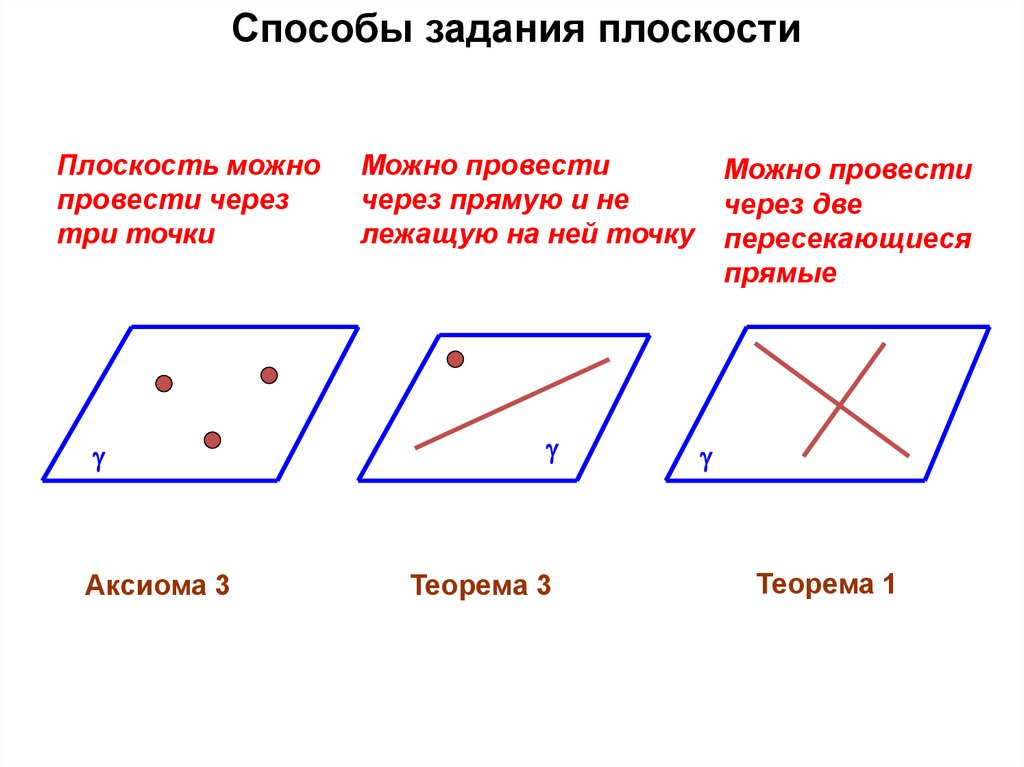
Способы задания плоскости
Плоскость можно
провести через
три точки
Аксиома 3
Можно провести
через прямую и не
лежащую на ней точку
Теорема 3
Можно провести
через две
пересекающиеся
прямые
Теорема 1