Моделирование продольного движения. Передаточные функции продольного движения. Структурные схемы КППД

1.

Лекция №5 Моделирование продольного движения. Передаточные
функции продольного движения. Структурные схемы КППД
При выделении продольного движения полагается, что силы и моменты, определяющие
боковое движение, при маневрировании в вертикальной плоскости не изменяются
FzT 0, Mx 0, My 0 или
mW FxT
mW FyT
I z z M z
z 0, x 0 , y 0
проекции вектора внешних сил на оси траекторной СК, Wземная скорсть
(2.1)
z cos y sin
xg W cos cos
yg W sin
(2.2)

2.

ya
yT
xТ
x
Y
P
W
и
в
0
иу
xа
их
V
X
O
mg
Г
в
и
в у
V и х
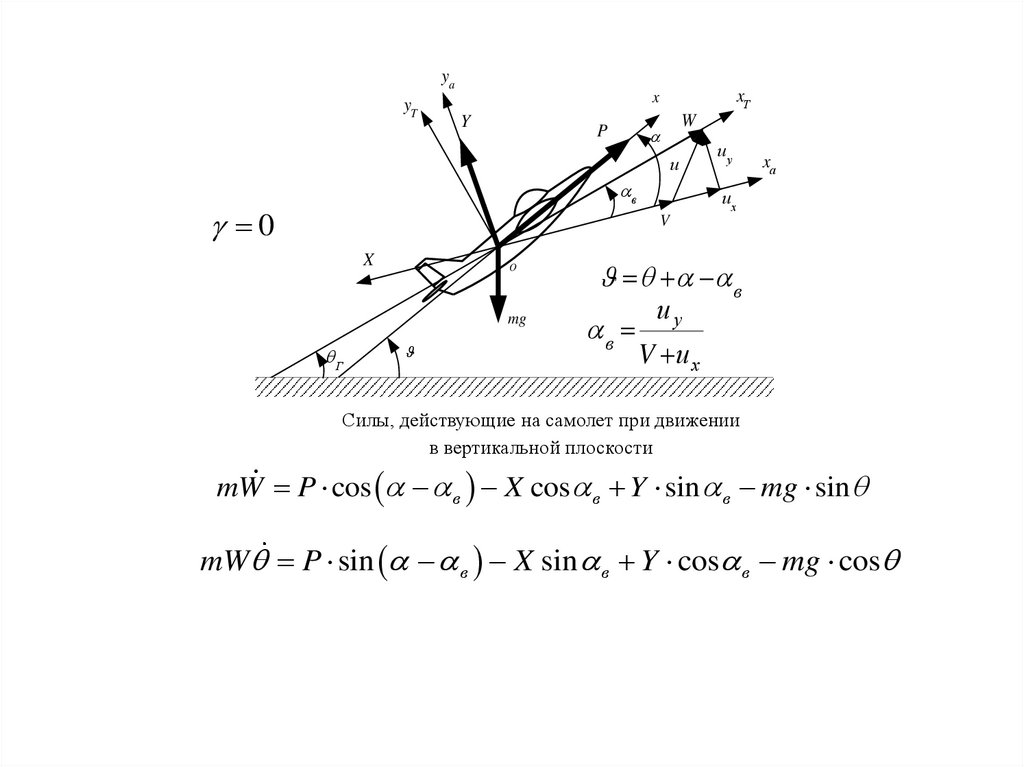
Силы, действующие на самолет при движении
в вертикальной плоскости
mW P cos в X cos в Y sin в mg sin
mW P sin в X sin в Y cos в mg cos

3.

Линеаризация уравнений продольного движения
Рассмотрим частный случай продольного движения – прямолинейное,
равномерное движение в спокойной атмосфере (ветер отсутствует)
FxТ P0 cos 0 X 0 mg sin 0 0
0
FyТ P0 sin 0 Y0 mg cos 0 0
(2.5)
0
M z0 0
Индексом «0» обозначены балансировочные значения соответствующих величин.
P P V , H , руд
P P p p PV V P H H
X X V , H , , в
X X в в X V V X H H X
Y Y V , H , , в
M z M z V , H , , , z , в
P p , XV
Y Y в в Y V V Y H H Y
M z M z в в M zV V M zH H
M z M z M z z z
и др., являются частными производными нелинейных функций в
точке, соответствующей выбранному невозмущенному режиму.

4.

Осуществим линеаризацию уравнений, получим уравнения продольного движения:
Полученные уравнения в приращениях являются линейными, однако они справедливы в
ограниченных значениях параметров
V аVx V аxH H а x а x аx p p а x в в а x в в ;
аVy V а yH H а y а y p p аY в в а y в в .
(2.14)
z m zz z m z m z mVz V mHz H m вz ( в )
xg V cos 0 cos 0 V0 sin 0 cos 0 V cos 0
yg V sin 0 V0 cos 0 V0
в
Здесь
X в
а x в
m
H
H
X
P
cos 0
Y P sin 0
а
H
аy
m
mV0
X 0 P0 cos 0
в
V
V
P p cos 0
а
p
y
Y P sin 0
Y P0 cos 0
аx
mV0
аVy
а y
m
mV0
mV0
Y в
в
аy
X P0 sin 0
p
а x
mV0
P
sin
Y P0 sin 0
0
m
аy p
а x в 0
mV0
m
ay в 0
a x g
X V PV cos 0
а
m
V
x
H
H
H
x
M z z
mz
Iz
z
M z
mz
Iz
.
.
M
mz z
Iz
M z в
mz
Iz
в
V
mz
M zV
Iz
H
mz
M zH
Iz

5.

Для решение уравнений движения ВС выполним преобразование Лапласа.
Оператор комплексной переменной р означает дифференцирование функции.
Например: L( V(t))
V(p) . После преобразования всех переменных уравнения
движения ВС , получим линейные системы уравнений, позволяющие определить все
переменные в преобразованиях Лапласа. Для нахождения зависимости параметров во
времени, необходимо результат решения системы уравнений преобразовать с
помощью обратного преобразователя Лапласа во временные зависимости.
Наиболее слабой перекрестной связью в уравнениях оказывается связь по высоте
полета, что объясняется малым градиентом изменения плотности атмосферы по
высоте. В результате кинематическое уравнение изменения высоты становятся
независимыми. Рассматривая изменение параметров ВС во времени, можно
отметить, что угловые параметры ВС изменяются быстро. При этом скорость ВС
существенных изменений не претерпевает. Это позволяет разделить движение ВС
на короткопериодическое (угловое) и длиннопериодическое (движение ЦМ),
практически независимые . Параметр скорость т.о. исключается из уравнений и
первое уравнение становится автономным.

6.

Система дифференциальных уравнений (2.14) характеризует динамику реакции
самолета на нарушение продольной балансировки, не приводящей к появлению
значительных приращений координат (для углов – до 10º, для скорости – до 15 мс-1).
Одна из особенностей уравнений динамики движения самолета – слабые
перекрестные связи уравнений (2.14). Наиболее слабой оказывается связь по высоте
полета, что объясняется малым градиентом изменения плотности от высоты и им
можно пренебречь. В результате кинематическое уравнение изменения высоты
оказывается автономным y g V0
и степень уравнений 2.14 понижается до 4.
Характеристический полином системы имеет вид:
р р 4 а3 р3 а2 р 2 а1 р а0
(2.16)
Свободное продольное движение самолета содержит две колебательные
составляющие с резко различающейся скоростью затухания
р р 2 2 к к р к2 р 2 2 Д Д р Д2
(2.17)
где первый соответствует большим корням, а второй – малым,
к 1,82 с-1,
к 0,36
Д 8 10 2
Д 0,075
с-1,
,
что
соответствует
колебаний
периодам
Т к 3,7 с. Т Д 80 с

7.

3
j
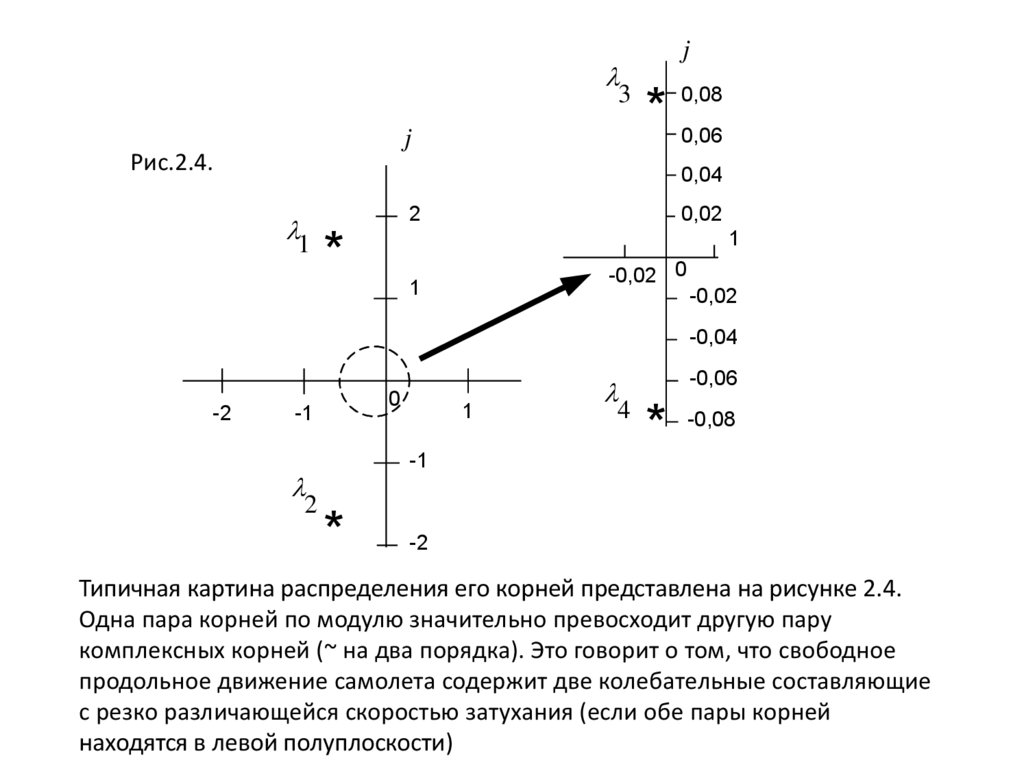
Рис.2.4.
j
*
0,08
0,06
0,04
1
2
0,02
1
*
-0,02 0
1
-0,02
-0,04
-2
0
-1
-1
2
1
*
4
-0,06
*
-0,08
-2
Типичная картина распределения его корней представлена на рисунке 2.4.
Одна пара корней по модулю значительно превосходит другую пару
комплексных корней (~ на два порядка). Это говорит о том, что свободное
продольное движение самолета содержит две колебательные составляющие
с резко различающейся скоростью затухания (если обе пары корней
находятся в левой полуплоскости)

8.

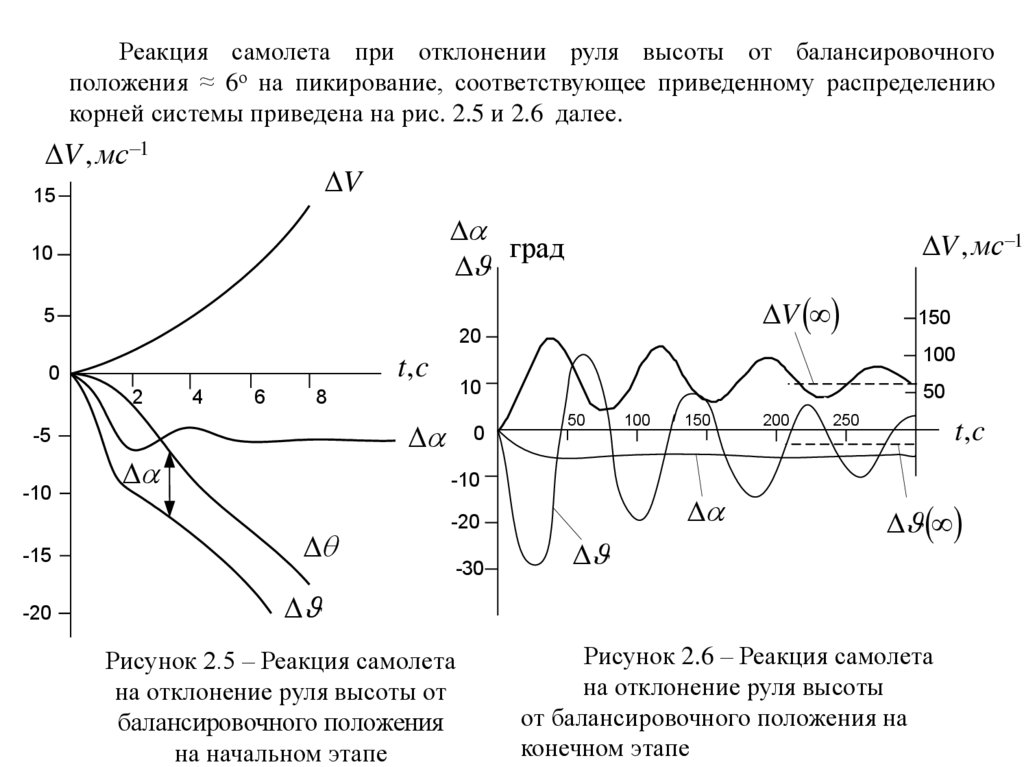
Реакция самолета при отклонении руля высоты от балансировочного
положения ≈ 6о на пикирование, соответствующее приведенному распределению
корней системы приведена на рис. 2.5 и 2.6 далее.
V , мc 1
V
15
град
10
V , мс 1
V
5
20
2
4
6
-15
-20
10
8
-5
-10
100
t, c
0
0
50
50
-10
150
150
-20
-30
100
200
250
t, c
Рисунок 2.5 – Реакция самолета
на отклонение руля высоты от
балансировочного положения
на начальном этапе
Рисунок 2.6 – Реакция самолета
на отклонение руля высоты
от балансировочного положения на
конечном этапе

9.

На начальном этапе реакции (рисунок 2.5) происходит быстрое изменение
углов атаки, тангажа и наклона траектории на отрезке времени в несколько секунд.
Скорость полета на этом отрезке изменяется незначительно. (Большие корни).
Затем медленно начинает развиваться колебательный процесс нарастания скорости
полета (рисунок 2.6). При выполнении условия устойчивости, а в рассматриваемом
случае оно выполняется, самолет выйдет на новый режим горизонтального полета,
но на меньшей высоте и с большей скоростью, если не менять положения РУД.
Процесс выхода займет сотни секунд.
В переходном процессе на втором этапе угловое положение самолета и угол
наклона траектории будут изменяться синхронно с колебаниями скорости.
Приращение α практически неизменно (малые корни). В динамике полета
движение самолета на начальном этапе называют короткопериодическим
движением (КПД), а дальнейшее развитие реакции – длиннопериодическим
движением (ДПД).
Поскольку на начальном этапе реакции самолета его скорость сравнительно
мало меняется, то можно пренебречь приращением скорости. Тогда во всех
уравнениях динамики исчезнут все составляющие, зависящие от скорости, а
первое уравнение системы (2.14) потеряет смысл, поскольку именно оно
характеризует процесс изменения скорости полета. Ниже приводится
математическая модель КПД продольного движения*.

10.

(2.18)
p
в
p а y ay P P ayв в
L
аy ay p ay в
z amz z am am am в в z p аmz z am p am amв в ;
z
z
z
z
z
в
z
z
z
в
z
xg V cos 0
yg Vy V0
1
z ;
p
Считая все коэффициенты постоянными, выполним преобразование Лапласа
первых трех уравнений 2.18.
Характеристический полином формируется раскрытием определителя
p
p 0
1
ay
0
am p am
p am z
z
1
p p 2 аmz am a y p am a y amz
z
Здесь
z
1
p
z
z
p 2 2 p 2
2 amz am a y
z
z
z
2 a m a y am
z
z
am z am a y
z
z
2 am a y am z
z
z
z
z
квадрат частоты собственных колебаний в
короткопериодическом движении;
относительный коэффициент затухания

11.

Здесь в первом столбце записаны коэффициенты уравнений при переменной θ, во
втором – коэффициенты при α, в третьем – коэффициенты при z
к р р 2 2 к к р к2
(2.20)
Правомерность выделения уравнений КПД подтверждается близостью корней
полинома (2.20) к корням полинома (2.17), соответствующего малым корням
Отклонения руля высоты входит в уравнения движения центра масс (верхнее
уравнение в 2.18). Физически это объясняется тем, что подъемная сила РВ, как
всякая сила, приложенная не к ЦМ, помимо момента относительно поперечной оси
ОZ, создает линейное ускорение по нормали к траектории. В результате появляется
дополнительная скорость поворота траектории в
. Указанный эффект
принято называть непосредственным влиянием РВ на движении ЦМ. Вследствие
относительной малости подъемной силы РВ его влияние на поворот траектории
невелико и обычно им пренебрегают, т.е. полагают коэффициент а в 0
y

12.

Передаточную функцию самолета по α можно определить как отношение двух
полиномов ** Этот способ формирования передаточных функций в литературе носит
название правила Крамера.
р р
W р
в р p
в
p
p полином, который вытекает из частного определителя,
формируемого из определителя p заменой столбца
- характеристический полином КПД
p
0
p 0
amв
1
0
коэффициентов при α столбцом коэффициентов правой
части уравнений (2.18) при управляющем воздействии в
0
z
p am amв
z
z
1
p
Реакция самолета по углу атаки на отклонение РВ от балансировочного
положения описывается колебательным звеном
в
к
W p 2
p 2 p 2
в
2
где к в
(2.23)
аmв
z
2
коэффициент
усиления самолета по
углу атаки.

13.

При анализе динамики продольного движения важную роль играет связь скорости
изменения угла наклона траектории с углом атаки, вытекающая из первого
уравнения системы (2.18), если пренебречь сравнительно слабым влиянием
проекции силы тяги и подъемной силы руля высоты ( a y P 0 и a y в 0 ), получим:
L
a y
1
T
1
,
T p
(2.24)
т.е. скорость поворота траектории зависит главным образом от угла атаки.
T постоянная времени – один из показателей маневренности самолета
Несущие способности планера самолета практически целиком зависят от
производной c y
и последняя определяет эффективность изменения направления
траектории полета в вертикальной плоскости.

14.

Скорость поворота траектории определяется при прочих равных условиях
значением нормальной перегрузки
g
V
(n y cos )
Вывод передаточной функции по приращению нормальной перегрузки
используем связь 2.24, 2-23
в
Wn ( p )
y
n y ( p )
в ( p)
kn в 2
y
p 2 2 p 2
где коэффициент усиления передаточной функции по перегрузке
kn в k в n y
y
Она отличается от передаточной функции по углу атаки (2.23) только
коэффициентом усиления, поскольку перегрузка не запаздывает по
отношению к α.

15.

Передаточной функции по угловой скорости
a y
p
z p 0
W в p
z
аmв amв p a y к в 2 T p 1 .
а y p a y
1
Здесь учтено, что
0
p
z
z
0
и
amв a y k в 2
z
z
1
T a y
p
1
z
к в 2 T p 1
z
z
p 2 2 p 2
(2.26)
Из сравнения передаточных функций (2.23) и (2.26) вытекает
z p T p 1
p
T

16.

Передаточные функции (2.23), (2.24), (2.26) используются для построения
структурных схем короткопериодического продольного движения (рисунок 2.7).
1-я форма
в
k в 2 T p 1
z
p 2 2 p 2
z
1
p
1
V0 H
T p 1
p
2-я форма
в
1 V0
k в 2
T p
p
p 2 2 p 2
n y
n y
H
g H
p2
Рисунок 2.7 – Структурные схемы продольного движения самолета

17.

,
T
0
3T
t
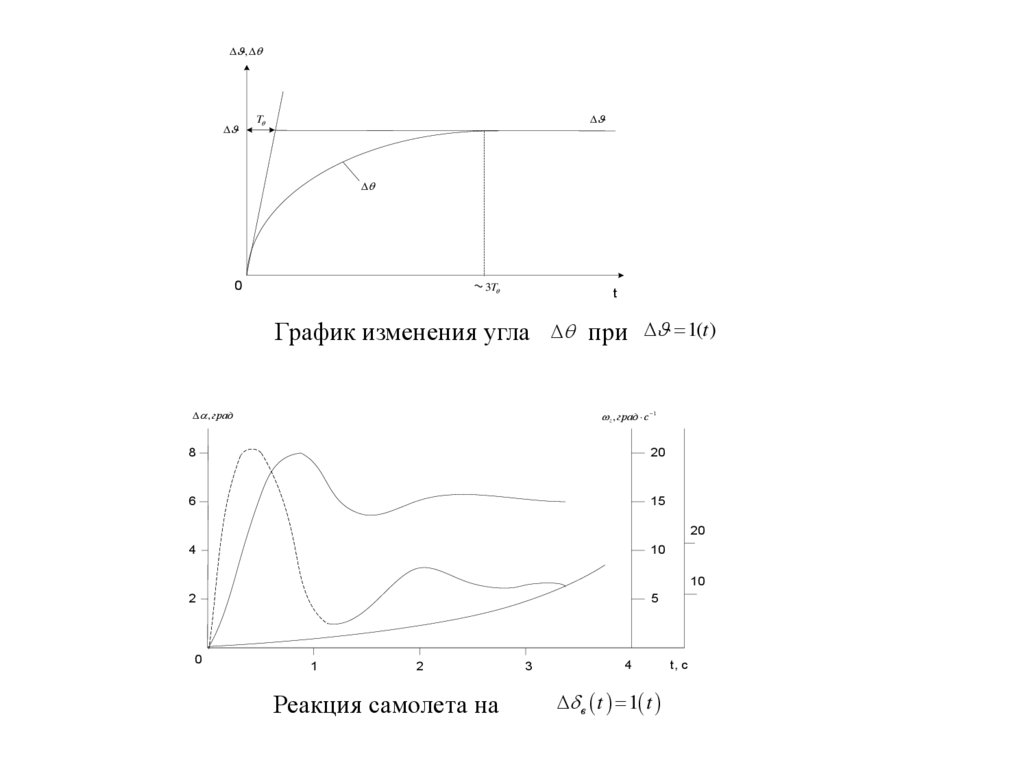
График изменения угла
, град
при 1(t )
z , град с 1
8
20
6
15
4
10
2
5
20
10
0
1
2
Реакция самолета на
3
4
в t 1 t
t, c

18.

2.4. Влияние вертикальной составляющей скорости ветра
Перейдем к оценке влияния ветра на продольное движение самолета. В системе
уравнений короткопериодического движения (КПД) влияние ветра учитывается
координатой αв в кинематическом уравнении системы (2.18):
в
р
0
в р 0
0
0
в
р аmz p amz p
z
z
1
p
1 1
p amz p
р
z
W р
2
в р р 2 р 2
в
Uy
V0

19.

a y
р
р 0
z
1
.
0
.
am p am
z
1
z
0 (am p am ) p
z
z
1
.
(аm p am ) p
z p
в
z
W p
2 z
z
в p
p 2 p 2
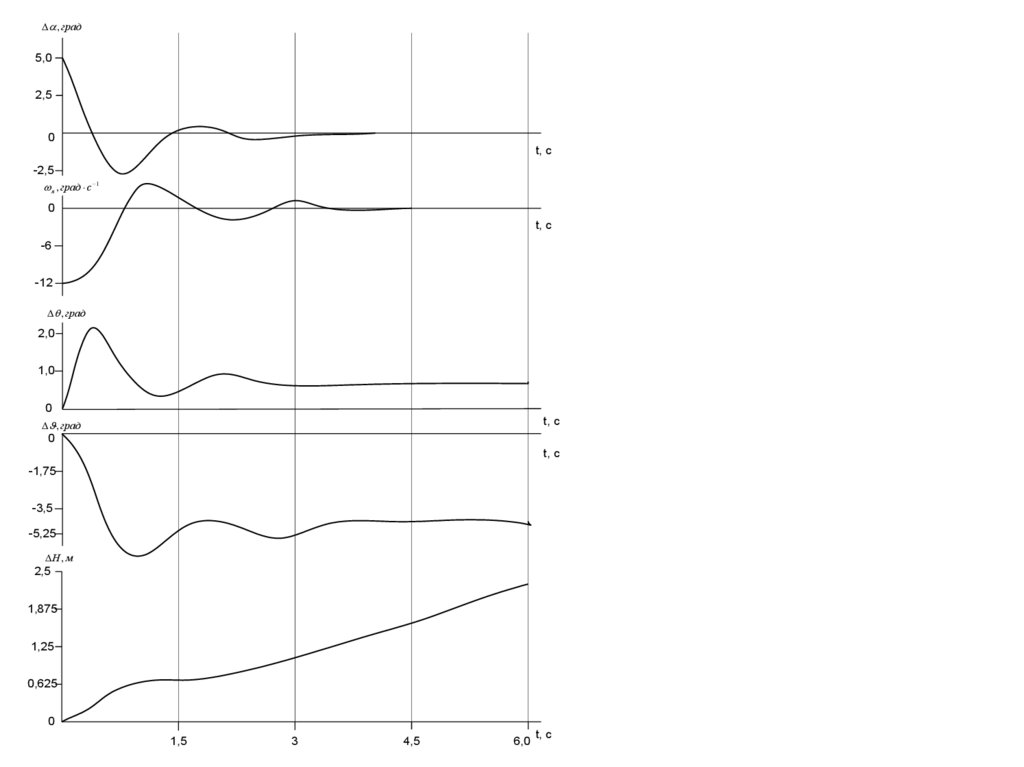
Реакция самолета на ступенчатый ветер показана на рисунке 2.11

20.

, град
5,0
2,5
0
t, c
-2,5
я , град с 1
0
t, c
-6
-12
, град
2,0
1,0
0
t, c
, град
0
t, c
-1,75
-3,5
-5,25
Н , м
2,5
1,875
1,25
0,625
0
1,5
3
4,5
6,0
t, c

21.

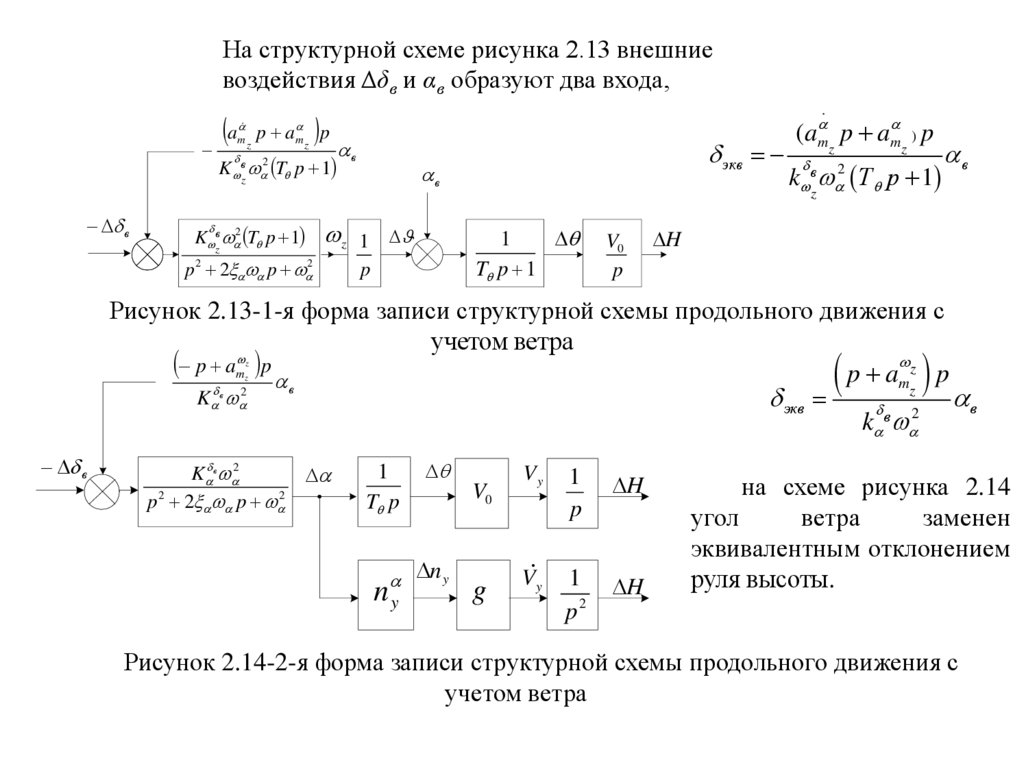
На структурной схеме рисунка 2.13 внешние
воздействия Δδв и αв образуют два входа,
a p a p
mz
mz
K в 2 T p 1
.
(am p am ) p
в
K в 2 T p 1
z 1
p 2 2 p 2
p
z
z
z
k Т р 1
в
z
в
экв
в
z
1
T p 1
V0
p
2
в
H
Рисунок 2.13-1-я форма записи структурной схемы продольного движения с
учетом ветра
z
p am p
p
a
mz p
в
2
K
экв
в
в 2
k
z
z
в
в
K в 2
p 2 2 p 2
1
T p
ny
V0
n y
g
Vy
1
p
H
V y
1
p2
H
на схеме рисунка 2.14
угол
ветра
заменен
эквивалентным отклонением
руля высоты.
Рисунок 2.14-2-я форма записи структурной схемы продольного движения с
учетом ветра