Линейные неравенства с одной переменной и их решение. Изображение решения линейного неравенства на числовой прямой

1.

Линейные неравенства
с одной переменной и их решение.
Изображение решения линейного
неравенства на числовой прямой
х
-3
1
х

2.

ПОВТОРИМ!

3.

4.

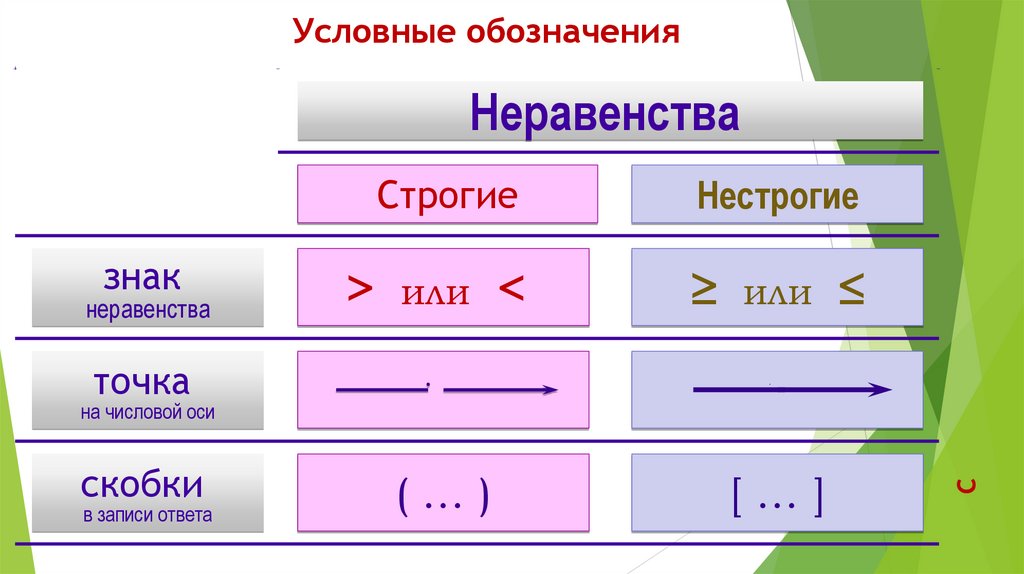
Условные обозначения
Неравенства
знак
неравенства
Строгие
Нестрогие
> или <
≥ или ≤
(…)
[…]
точка
скобки
в записи ответа
С
на числовой оси

5.

6.

Рассмотрим неравенство 5х – 11 > 3
при х = 4
при х = 2
5 • 4 – 11 > 3; 9 > 3 – верно;
5 • 2 – 11 > 3, - 1 > 3 – неверно;
Решением неравенства с одной переменной называется значение
переменной, которое обращает его в верное числовое неравенство.
Решить неравенство – значит найти все его решения или доказать,
что их нет.
Неравенства, имеющие одни и те же решения, называют
равносильными.
Неравенства, не имеющие решений, тоже считают равносильными

7.

Устно
1. Является ли число -3 решением неравенства х + 1 ≥0
2. Решите неравенство -2а ≤ 6
а) (+∞; 3) б) [-3; + ∞) в) [4 +∞) г) (-∞; -3]
3. Какое наименьшее целое число является решением неравенства?
х/5 > 1
а) 5 б) 1 в) 2 г) 6
4. Проверь, верно ли выполнено решение неравенства?
-2(х+4) < 1 – (5х – 3);
-2х – 8 < 1 – 5х + 3;
-2х – 8 < 4 – 5х;
-2х-5х < 4 + 8;
-7х < 12;
х < - 12/7

8.

Алгоритм решения
неравенств одной переменной
С
1. Раскрыть скобки (если они есть);
2. Перенести неизвестные слагаемые в одну часть, а
известные в другую;
3. Упростить выражения в левой и правой частях неравенства;
4. Решить простейшее неравенство;
5. Изобразить решения неравенства на числовой прямой (если
необходимо);
6. Записать ответ.

9.

Решить неравенство
–х – 4 < 3 (7 – 3х) + 7
–х – 4 < 21 – 9х + 7
раскрыть скобки
перенести неизвестные слагаемые в одну
часть, а известные в другую (знаки этих
слагаемых меняются на противоположные)
–х + 9х < 21 + 4 + 7
привести подобные слагаемые
8х < 32
решить простейшее неравенство
х < 32 : 8
х<4
записать ответ
Ответ: х < 4 или (– ; 4)
С
1.

10.

2.
Найти наименьшее целое решение неравенства
домножить обе части неравенства на 8
3х – 0,5(7х – 3) < 2 – 0,125(7 – 9х)
24х – 4(7х – 3) < 16 – (7 – 9х)
24х – 28х + 12 < 16 –7 + 9х
24х – 28х – 9х < 16 –7 –12
–13х < – 3
х > – 3:(–13)
раскрыть скобки
перенести неизвестные слагаемые в одну
часть, а известные в другую (знаки
слагаемых изменяются); привести подобные
слагаемые
решить простейшее неравенство (при делении на
отрицательное число знак неравенства меняется)
С
х > 3/13
Ответ: наименьшее целое решение неравенства 1

11.

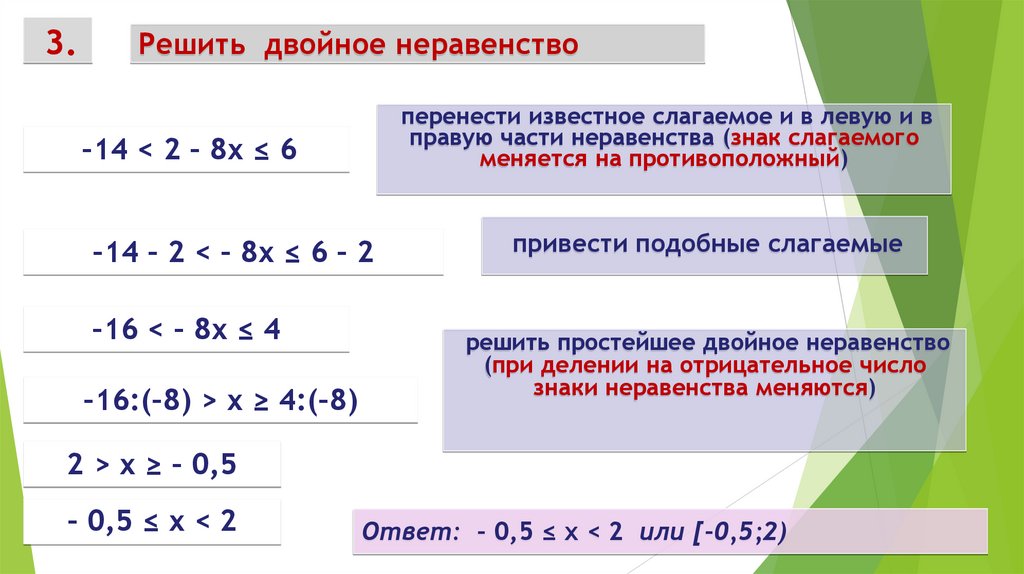
3.
Решить двойное неравенство
перенести известное слагаемое и в левую и в
правую части неравенства (знак слагаемого
меняется на противоположный)
–14 < 2 – 8х ≤ 6
–14 – 2 < – 8х ≤ 6 – 2
–16 < – 8х ≤ 4
–16:(–8) > х ≥ 4:(–8)
привести подобные слагаемые
решить простейшее двойное неравенство
(при делении на отрицательное число
знаки неравенства меняются)
2 > х ≥ – 0,5
– 0,5 ≤ х < 2
Ответ: – 0,5 ≤ х < 2 или [–0,5;2)

12.

Выполнить задания
1. Какое число является решением
неравенства 3 – 2х > 5
А) 4 Б) 0 В) 0,5 Г) -3
1. Какое число является решением
неравенства 3х – 1 > 4
А) 0 , Б) -0,3 В) 6 Г) 1
2. Решите неравенство -2х < 5
2. Решить неравенство -5х > 8
3. Решите неравенство х + 4 ≥ -1
3. Решите неравенство 2 + х ≤ -3
4. Решите неравенство
4. Решите неравенство
5х – 2(х - 4) ≤ 9х + 20
2х – 3(х + 4 ) < х + 12
5.
Найти
область
определения 5. Найти область определения выражения
выражения
х 3
5
х 2
3

13.

проверка
I вариант
1.
2.
3.
4.
5.
-3
(-2,5; + ∞)
[ -5; + ∞)
[-2; + ∞)
[3; + ∞)
II вариант
1.
2.
3.
4.
5.
6
(-∞; - 1, 6)
(-∞; -5]
(-12; + ∞)
[-2; + ∞)

14.

Самостоятельная работа
1.6 – 2(–2х – 5)< х + 8
2.х – 4 ≥ 3(–х – 7)
3. –2х – 43 <–7
5
4. 3х – 36 ≥ –6
8
5. –7,5 ≤ 5х + 1,5≤ –3,5
6. 22 < 3 – 4х < 30
Вариант 2
1. 4 – 2(–2х – 2)> 2х +5
2. х + 9 ≤ 5(–х – 3)
3. –6х – 14 > –12
5
4. 3х – 36 ≤ –7
3
5. –5,5 ≤ 5х + 3,5≤ –0,5
6. 34 < 6 – 2х < 44
С
Вариант 1