Similar presentations:
Преобразования графиков элементарных функций
1.
2. Преобразование графиков функций. Т1. Симметрия относительно оси Ох
уy = f(x)
график исходной
функции
y = - f(x)
+с
0
-с
y = f(x)
в
х
y = - f(x)
симметричное
отображение
относительно
оси Ох
у= 3х+4
у= -3х-4= -(3х+4)
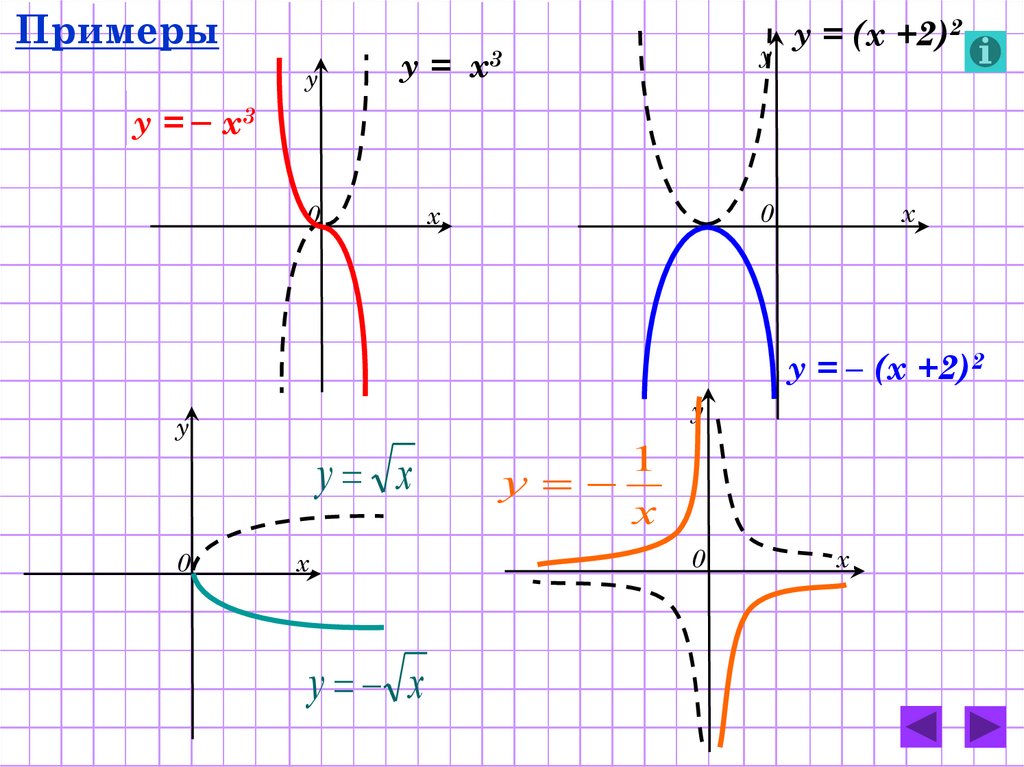
3.
Примерыу
у = х3
у
0
х
0
у = (х +2)2
у = – х3
х
у = – (х +2)2
у
у
у х
0
х
у х
1
у
х
0
х
4. Преобразование графиков функций. Т2. Симметрия отображение относительно оси Оу
уy = f(x)
график исходной
функции
y = f(-x)
0
-a
х
+a
y = f(-x)
симметричное
отображение
относительно
оси Оу
-с
y = f(x)
у= 3х+4
у= -3х+4
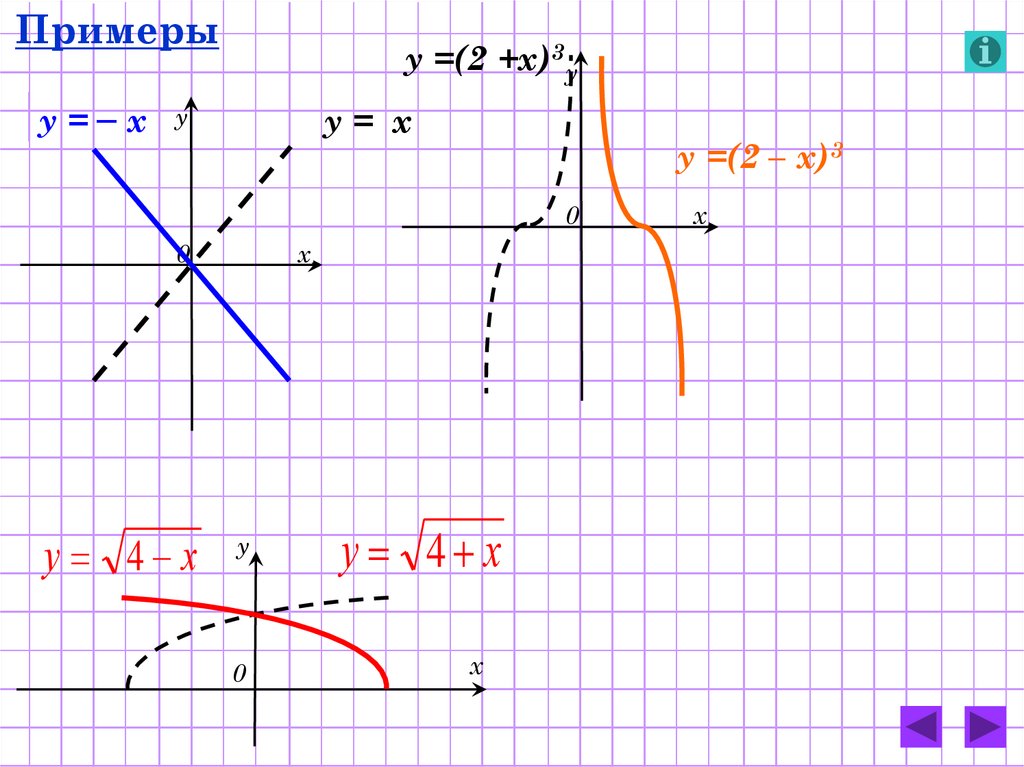
5.
Примерыу=–х
у =(2 +х)3 у
у= х
у
у =(2 – х)3
0
0
у 4 х
х
у
0
у 4 х
х
х
6. Преобразование графиков функций. Т3. Параллельный перенос по оси Оу
уy = f(x)
график исходной
функции
y = f(x) + a
+a
х
0
y = f(x)
-a
y = f(x) + a
параллельный
перенос вверх
по оси Оу
y = f(x) – a
y = f(x) - a
параллельный
перенос вниз
по оси Оу
7.
Примерыу = х3+3
у
у
у = х+4
у
х
0
4
3
х
0
у
0
у
2 –2
у
=
х
-2
0
х
у х 3
3
0
х
х
-2
1
у 2
х
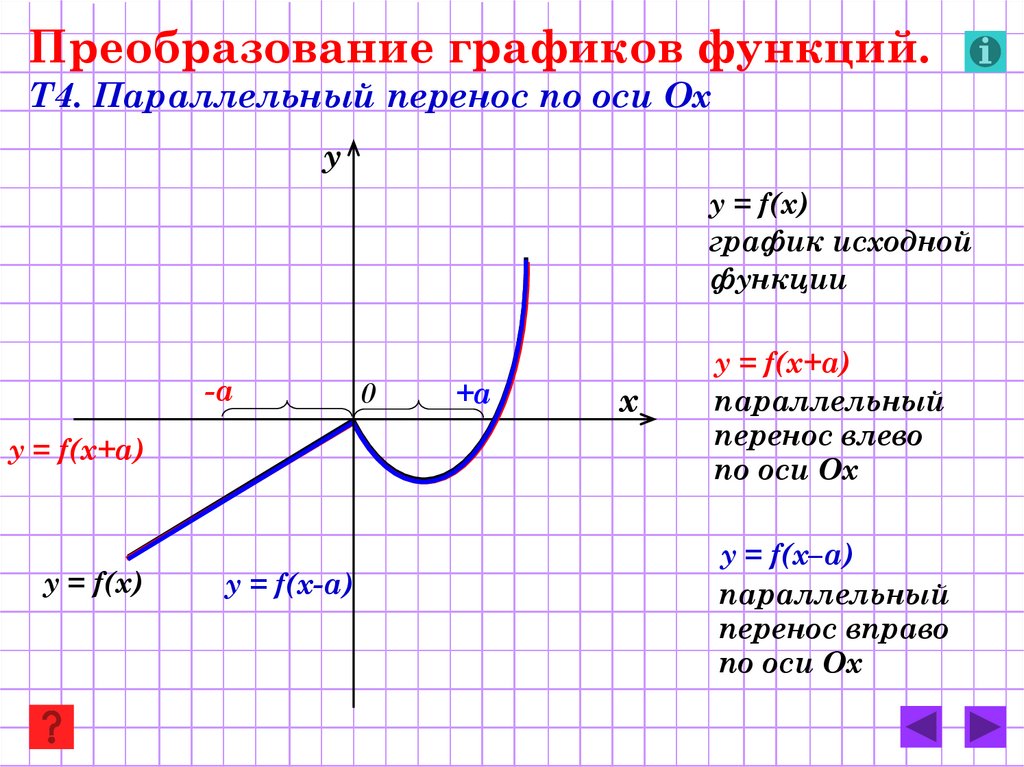
8. Преобразование графиков функций. Т4. Параллельный перенос по оси Ох
уy = f(x)
график исходной
функции
-a
y = f(x+а)
y = f(x)
y = f(x-а)
0
+a
х
y = f(x+a)
параллельный
перенос влево
по оси Ох
y = f(x–a)
параллельный
перенос вправо
по оси Ох
9.
Примерыу =(х –4)2
у
у
у х 2
х
0
4
2
у
-3
1
у
х 3
х
0
0
х
10. Преобразование графиков функций. Т5. Графики функций, содержащих модуль.
уy =|f(x)|
y = f(x)
0
х
y = f(x)
график исходной
функции
y =|f(x)|
часть графика,
лежащая над осью Ох
сохраняется, часть
лежащая ниже оси Ох,
симметрично
отображается
относительно оси Ох
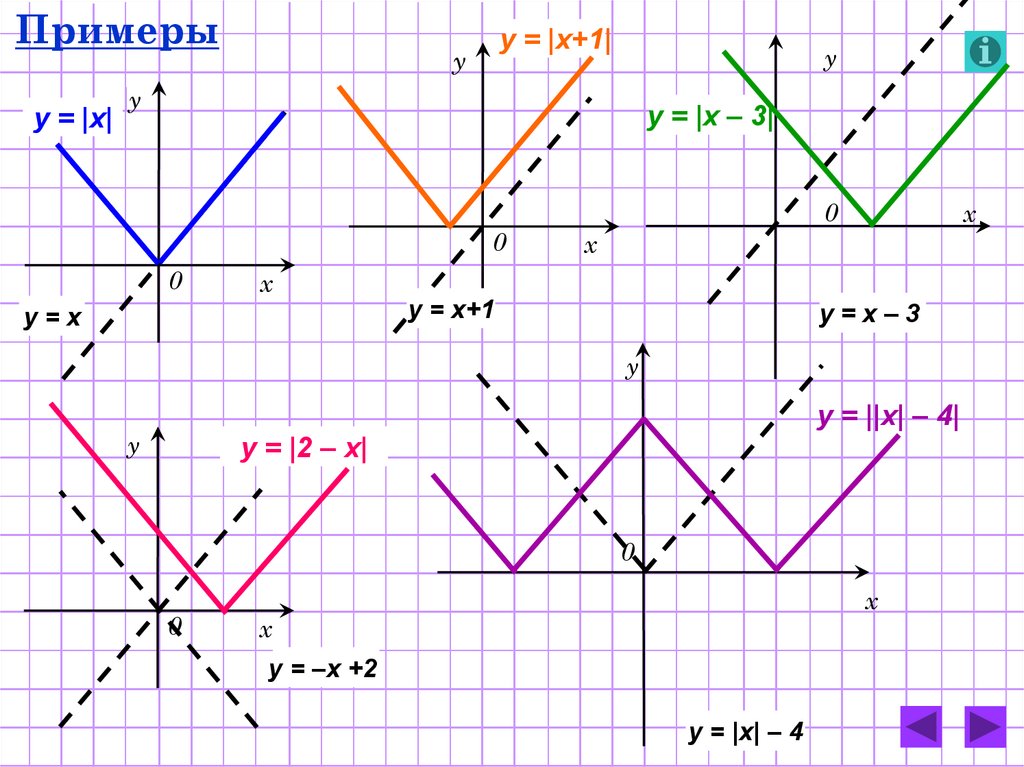
11.
Примерыy = |x|
y = |x+1|
у
у
у
y = |x – 3|
0
0
0
х
х
х
y=x–3
y = x+1
y=x
у
у = ||х| – 4|
у
y = |2 – х|
0
0
х
х
y = –х +2
y = |x| – 4
12. Преобразование графиков функций. Т6.Графики функций, содержащих модуль.
уy = f(x) график исходной
функции
y = f(x)
0
y = f(|x|)
х
y = f(|x|)
часть графика
при х > 0 сохраняется,
она же симметрично
отображается
относительно
оси Оу
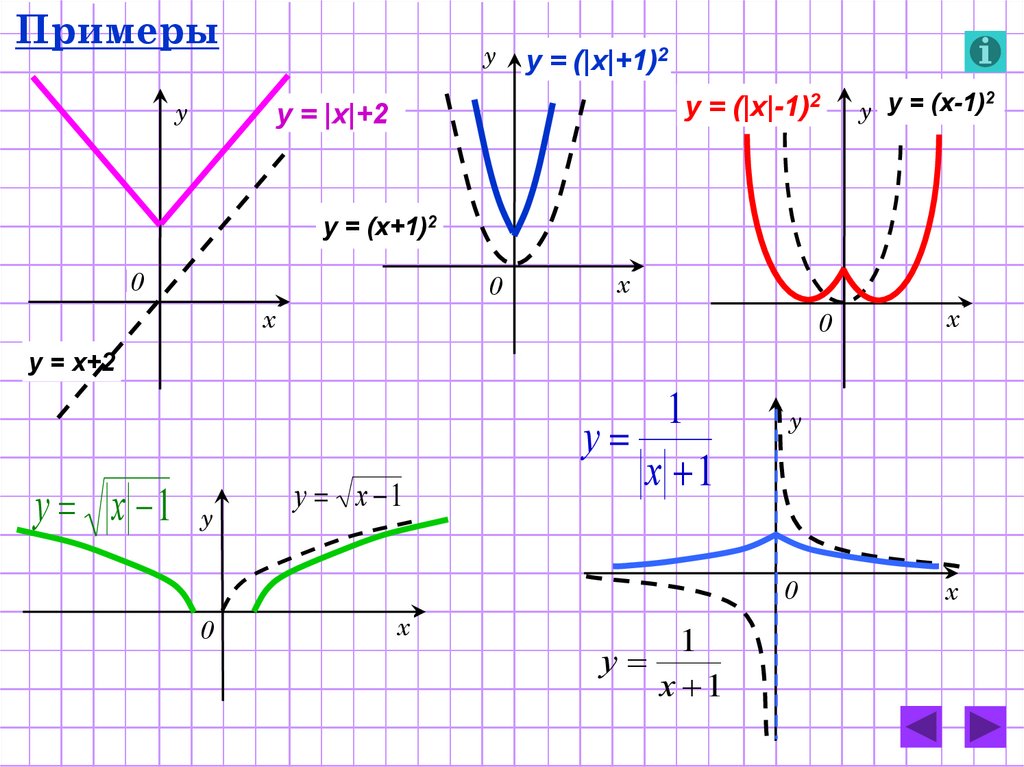
13.
Примерыу
у
y = (|x|+1)2
y = (|x|-1)2
y = |x|+2
у y = (x-1)
y = (x+1)2
0
0
х
х
0
х
y = x+2
у х 1 у
у х 1
1
у
х 1
у
0
0
х
у
1
х 1
х
2
14. Преобразование графиков функций. Т7.1. Растяжение вдоль оси Оу
уy = 2f(x)
y = f(x)
график исходной
функции
2
1
х
0
y = f(x)
-1
-2
y = kf(x)
растяжение вдоль
оси Оу в k раз, если
k>1
(на рисунке k = 2)
15. Преобразование графиков функций. Т7.2. Сжатие вдоль оси Оу
уy = f(x)
график исходной
функции
y = 1/2f(x)
y = f(x)
1
1/2
0
х
-1/2
-1
y = kf(x)
сжатие вдоль
оси Оу в 1/k раз,
если k < 1
(на рисунке k = 1/2)
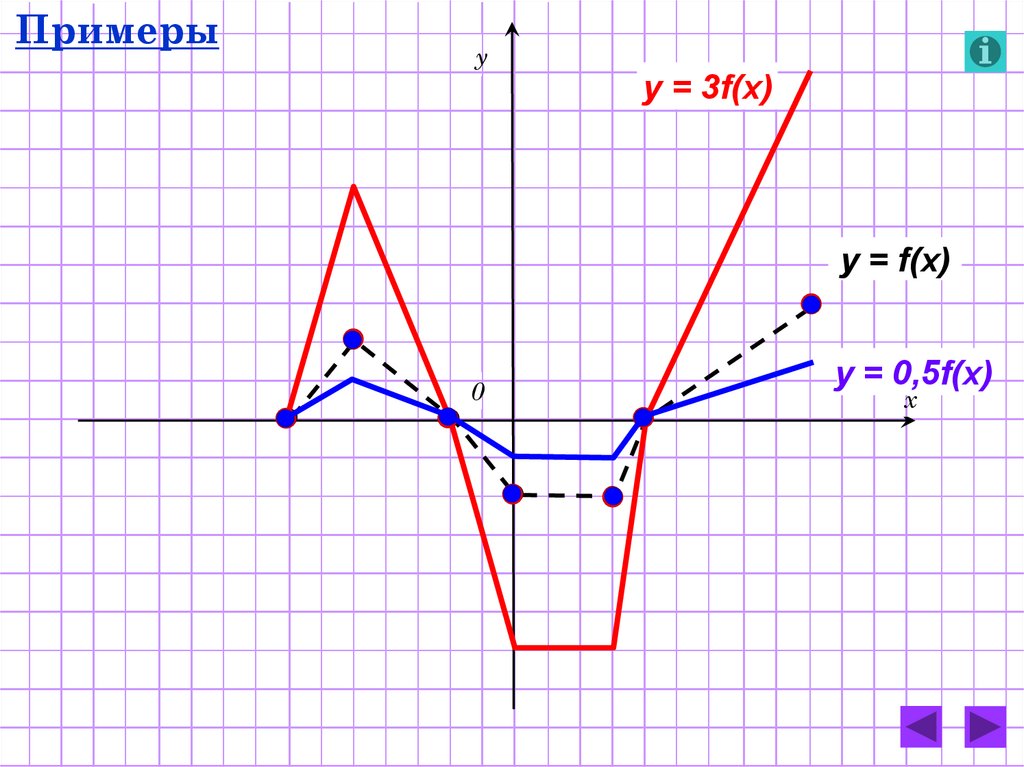
16.
Примерыу
y = 3f(x)
y = f(x)
0
y = 0,5f(x)
х
17. Преобразование графиков функций. Т8.1. Сжатие вдоль оси Ох
уy = f(x)
график исходной
функции
y = f(2х)
-2 0
1
-1
y = f(x)
2
х
y = f(kx)
сжатие вдоль
оси Ох в k раз если
k>1
(на рисунке k = 2)
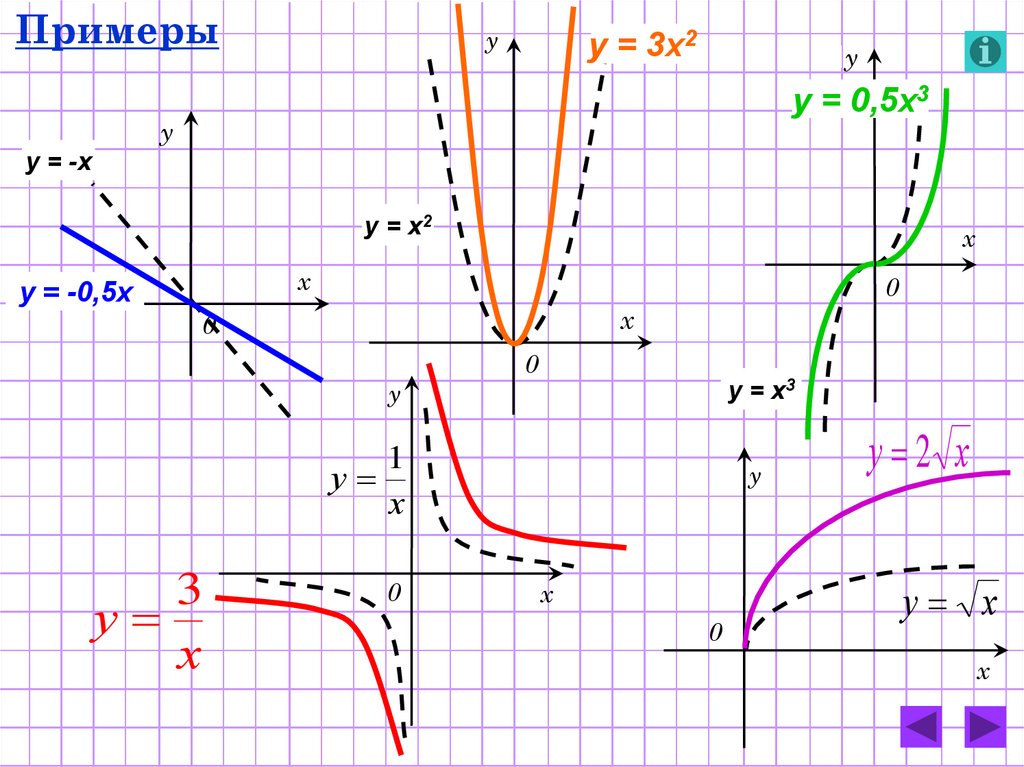
18.
Примерыу
y = 3x2
у
y = 0,5x3
у
y = -x
y = x2
х
х
y = -0,5x
0
х
0
у
у
3
у
х
0
y = x3
1
х
0
у
х
0
у 2 х
у х
х
19. Преобразование графиков функций. Т8.2. Растяжение вдоль оси Ох
уy = f(x)
график исходной
функции
y = f(x)
-2
y = f(2х)
-1
0
1
2
х
y = f(kx)
растяжение вдоль
оси Ох в 1/k раз, если
k<1
(на рисунке k = 1/2)
20.
Примерыу
0
х
y = f(x)
y = f(3х)
y = f(0,5х)
21.
Преобразование графиков функций.Композиция преобразований
F(x)= kf(ax-b)+d
1) Параллельный перенос по оси абсцисс (Ох)
F(x)= f(x-b)
2) Растяжение/сжатие вдоль оси Ох
F(x)= f(аx-b)
3) Растяжение/сжатие вдоль оси ординат (Оу)
F(x)= kf(x-b)
4) Параллельный перенос по оси Оу
F(x)= kf(ax-b)+d
22.
Примерыфункция
Приемы построения графика функции
у = 3х+3
у=х
у = 2(х+2)2
у = х2
→
у = 3х
растяжение по Оу
→
→
перенос вверх на 3
у = (х + 2)2
влево на 2
у = 3х + 3
→
у = 2(х + 2)2
растяжение по Оу
-
у = -0,5(х–1)2
у = х2 → у = (х -1)2 → у = 0,5(х -1)2 → у = - 0,5(х -1)2
у 2 х 1
у х → у 2 х
2
у
х 1
1
у
х
вправо на 1
сжатие по Оу
растяжение
→
влево на 1
→
отображение отн. Ох
у 2 х
отображение
1
у
х 1
→
у 2 х 1
перенос вверх на 1
→
2
у
х 1
растяжение по Оу
23.
уy = (x+2)2
у
y = 2(x+2)2
y = x2
y = (x-1)2
2
y=x
y = 0,5(x-1)2
у
y = 3x
y=x
0
y = 3x+3
х
х
х
0
у
y = -0,5(x-1)2
0
у 2 х
у
у х
0
х
у 2 х 1
у 2 х
0
2
у
х 1
1
у
х 1
у
х 1
х
24. Используя правила параллельного переноса вдоль координатных осей, установите соответствие между формулой, задающей функцию и
Задание 1.Используя правила параллельного переноса вдоль
координатных осей, установите соответствие
между формулой, задающей функцию и правилом
преобразования ее графика.
1. у х 4 3
2. у х 3 3
3. у х 3
4 . у ( х 3) 2 3
1
5. у
3
х 3
6 . у ( х 3) 3
7 . у ( х 3) 2 3
График данной функции построен путем
параллельного переноса графика функции
у = f(x) :
1) - на 3 ед. вниз по оси Оу;
2) - на 3 ед. вправо по Ох и на 3 вниз по Оу;
3) - на 3 ед. вверх по оси Оу;
4) - на 3 ед.влево по оси Ох и на 3 вниз по Оу;
5) - на 3 ед. вправо по оси Ох;
6) - на 3 ед. влево по оси Ох и на 3 вверх по Оу;
7) - на 3 ед. вверх по оси Оу и на 3 вправо по Ох

















 mathematics
mathematics








