Основные теоремы теории вероятностей. Лекция № 2

1.

Мордовский государственный университет
им. Н. П. Огарева
Кафедра математического анализа
Лекция № 2
«ОСНОВНЫЕ ТЕОРЕМЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ»
доцент кафедры Табачкова Марина Юрьевна
Саранск – 2014

2.

УЧЕБНЫЕ ВОПРОСЫ:
1. Теоремы сложения и умножения
вероятностей
2. Формула полной вероятности и
формула Байеса
3. Повторные независимые испытания

3. Литература

1. Кремер Н.Ш. «Теория вероятностей и математическая
статистика». Учебник для вузов. М.: ЮНИТИ-ДАНА,
2009.
2. «Математика: Математический анализ. Теория вероятностей и математическая статистика». / Под ред.
А.Н. Данчула. М.: Изд. РАГС, 2005.
3. Гельман В.Я. «Решение математических задач средствами Excel: Практикум». Учебник для вузов. СПб.:
ПИТЕР, 2003.
4. «Сборник задач по математике». М.: Изд. РАГС, 2005.

4.

ПЕРВЫЙ ВОПРОС
Теоремы сложения и умножения
вероятностей

5.

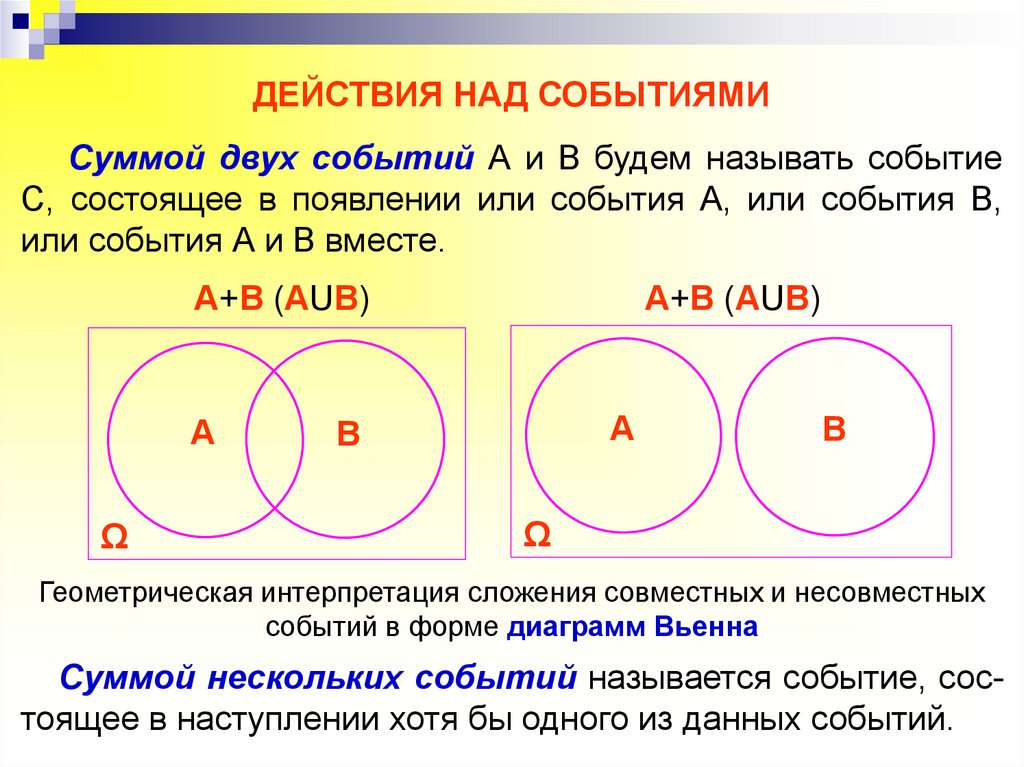
ДЕЙСТВИЯ НАД СОБЫТИЯМИ
Суммой двух событий А и В будем называть событие
С, состоящее в появлении или события А, или события В,
или события А и В вместе.
А+В (АUВ)
А
Ω
А+В (АUВ)
А
В
В
Ω
Геометрическая интерпретация сложения совместных и несовместных
событий в форме диаграмм Вьенна
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий.

6.

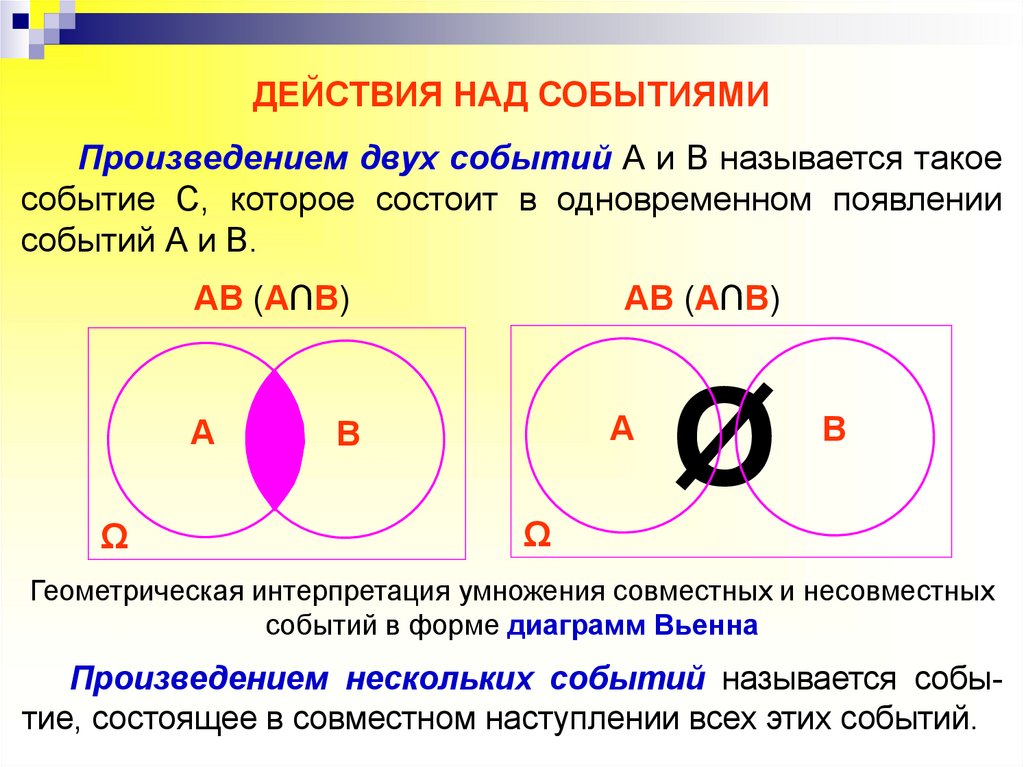
ДЕЙСТВИЯ НАД СОБЫТИЯМИ
Произведением двух событий А и В называется такое
событие С, которое состоит в одновременном появлении
событий А и В.
Ω
АВ (А∩В)
АВ (А∩В)
А
А
В
Ø
В
Ω
Геометрическая интерпретация умножения совместных и несовместных
событий в форме диаграмм Вьенна
Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий.

7.

Примеры.
1) Если опыт состоит в том, что по цели произведено 4
выстрела, и заданы события:
A0 — ни одного попадания,
A1 — ровно одно попадание,
A2 — ровно два попадания,
A3 — ровно три попадания,
A4 — ровно четыре попадания
то событие «не менее трех попаданий» есть: R A3 A4 .
2) Если экзаменационная сессия состоит из трех экзаменов, и заданы события:
B1 — сдача первого экзамена,
B2 — сдача второго экзамена,
B3 — сдача третьего экзамена,
то событие «успешная сдача сессии» есть: Q B1 B2 B3 .

8.

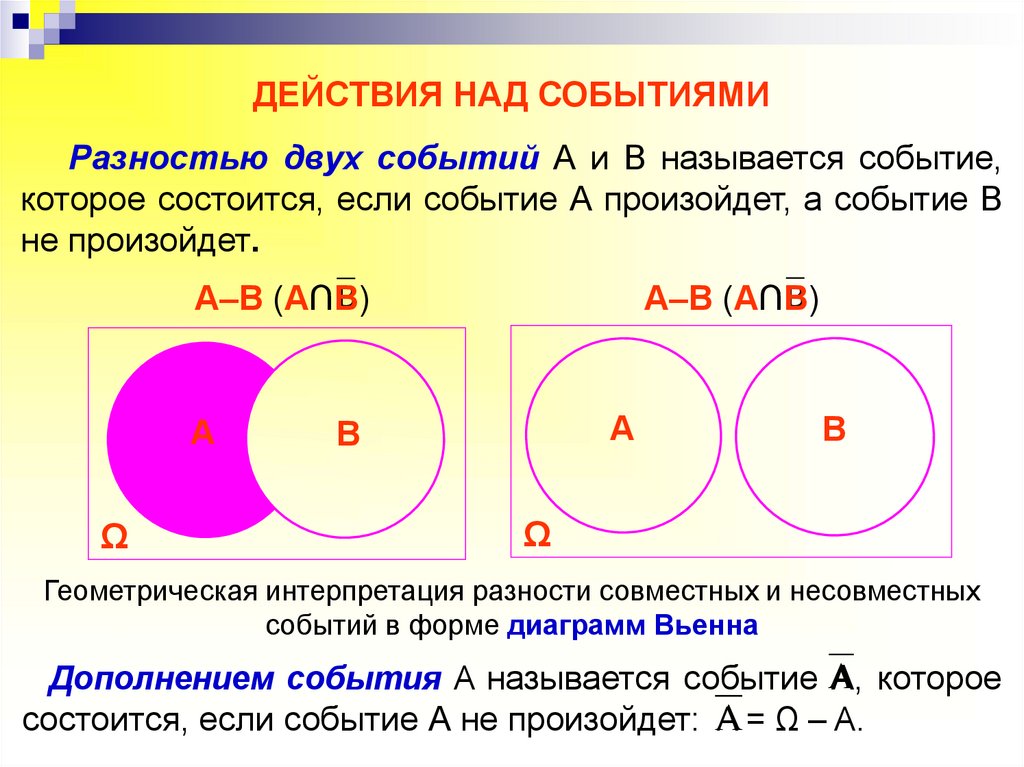
ДЕЙСТВИЯ НАД СОБЫТИЯМИ
Разностью двух событий А и В называется событие,
которое состоится, если событие А произойдет, а событие В
не произойдет.
В
А–В (А∩В)
А
Ω
В
А–В (А∩В)
А
В
В
Ω
Геометрическая интерпретация разности совместных и несовместных
событий в форме диаграмм Вьенна
Дополнением события A называется событие А
А, которое
состоится, если событие А не произойдет: А
A = Ω – A.

9.

Пример.
Свойства операций сложения и умножения событий:
Упростить выражение:
1. А + В = D
В + А( –
Aкоммутативность
B)( A B)( A сложения.
B ).
2. А + (В + С) = (А + В) + С – ассоциативность сложения.
Решение.
3.
D АВ
( A= ВА
B)(–Aкоммутативность
B)( A B ) ( AAумножения.
BA AB BB )( A B ).
4. A(BС) = (АВ)С – ассоциативность умножения.
AA
;
5. А(В + С) = АВ + АС; (А + В)С = АС + ВС – законы
BA умножения
AB A B относительно
AB ( A A) B сложения.
B B;
дистрибутивности
BB B, то
Поскольку
Из определения операций над событиями следуют
D (
B)( A B ) равенства:
B очевидные
B( A B ) BA BB
А + А = А; АА = А; А AB
+ Ω
=
Ω;
= А;
АΩAB
. А + Ø = А; АØ = Ø.

10.

Теорема сложения вероятностей несовместных событий
Доказательство:
Вероятность
суммы двух несовместных событий
Пустьсумме
в результате
испытания этих
из общего
числа n равновозравна
вероятностей
событий:
можных и несовместных исходов испытания событию А благоР(А+В)
=Р(А)В +–Р(В).
приятствует m1 случаев,
а событию
m2 случаев.
m1
m2
P ( A)
, P( B)
.
n
n
Так как события А и В несовместные, то ни один из случаев,
благоприятствующих одному из этих событий, не благоприятствует
другому. Поэтому событию А + В будет благоприятствовать m1 + m2
случаев:
m m
m
m
P( A B)
1
2
n
1
n
2
n
P ( A) P ( B ).

11.

Следствие 1:
Вероятность суммы конечного числа несовместных
событий равна сумме вероятностей этих событий:
Р(А1 А2 ... Аn ) Р(А1 ) Р(А2 ) ... Р(Аn ).
Следствие 2:
Сумма вероятностей событий, образующих полную
группу, равна единице:
Р(А1 А2 ... Аn ) Р(А1 ) Р(А2 ) ... Р(Аn ) 1.
Следствие 3:
Сумма вероятностей противоположных событий равна
единице:
Р(А) Р(А ) 1.

12.

Теорема сложения вероятностей совместных событий
Р(А В) Р(А) Р(В) – ?
?
Р(А)
Р(В)

13.

Условной вероятностью PA (B) ( P(B | A) или P(B/A) )
называется вероятность события В, вычисленная
при условии, что событие А уже произошло.
Пусть из общего числа n равновозможных и несовместных исходов испытания
событию А благоприятствует m случаев,
событию В — k случаев, а совместному
появлению событий А и B т.е. событию АВ
— l случаев (l ≤ m,l ≤ k)
P ( A)
m
l
, P ( AB) .
n
n
После того как событие А произошло, число всех равновозможных исходов
(случаев) сократилось с n до m, а число случаев, благоприятствующих событию
B с k до l.
l
l / n P( AB)
P( В | А)
m m/n
P( A)
или
P( AB) P( A) P( B | A)
Аналогично, для события В получаем
―
P( AB) P( B) P( A | B).

14.

Теорема умножения вероятностей
Вероятность произведения нескольких событий равна
произведению вероятностей этих событий, причем вероятность каждого следующего события вычисляется
при условии, что все предыдущие события имели место
P(A1 A2 ... An ) P(A1 )P(A2 | A1 )P(A3 | A1 A2 ) ... P(An | A1 A2 ... An-1 )
Для двух событий
P(AB) P(A)P(B | A) P( B) P( A | B)
Если события А и В независимы *
Для n независимых событий
Р(АВ) Р(А)Р(В).
n
n
i 1
i 1
P( A i ) P(A i )
* Событие В называется независимым от события А, если его
* События называются независимыми, если появление одного
вероятность не меняется от того, произошло событие А или
события не зависит от появления или не появления другого.
нет, т.е. Р(B | A) P ( B ), P ( A | B ) P ( A) .

15.

Теорема сложения вероятностей совместных событий
Вероятность суммы двух совместных событий равна
сумме вероятностей этих событий без вероятности их
произведения, т.е.
Пример.
Монету бросают 2 раза. Какова вероятность того, что хотя бы
Р(А"орел"?
В) Р(А) Р(В) P(AB).
один раз появится
Решение:
Обозначим события:
А – "появление орла при первом подбрасывании монеты",
В – "появление орла при втором подбрасывании монеты".
Необходимо определить вероятность события С = А + В.
Поскольку А и В совместные события, то
P(C ) P( A B) P( A) P( B) P( AB)
1 1 1 1 3
.
2 2 2 2 4

16.

Р(А+В+С)=Р(А)+Р(В)+Р(С)–Р(АВ)–Р(АС)–Р(ВС)+ Р(АВС)
Вероятность суммы нескольких совместных событий
А1, A2, ..., An равна разности между единицей и вероятностью произведения противоположных событий:
P(A1 AР(АС)
1 P( A
Р(АВ)
2 ... An )Р(А)
1 A2 A3 ... An ).
Для независимых:
P(A1 A2 ... An ) 1 P( A1 )P( A2 )P( A3 ) ... P( An ).
Р(В)
Р(С)
Для независимых и равных:
P(A1 A2 ... An ) 1 p 1 (1 p) .
n
Р(ВС)
Р(АВС)
n

17.

ВТОРОЙ ВОПРОС
Формула полной вероятности
и формула Байеса

18.

Формула полной вероятности
Если событие A может произойти только при условии
появления одного из событий (гипотез) H1, H2,..., Hn, образующих полную группу, то вероятность события A равна
сумме произведений вероятностей каждой из гипотез на
соответствующие условные вероятности события A:
n
P(A) P(H i )P(A|H i ),
i 1
где P(A)
- полная вероятность события А;
- вероятность гипотезы H i , при которой может
P(H i )
произойти событие A (i=1,2,…n);
P(A|H i ) - вероятность события A, вычисленная при
условии наступления гипотезы H i (i=1,2,…n).

19.

Формула Байеса :
P(H i )P(A | H i )
Р(Н i | A) n
P(H )P(A | H )
i
i
.
i 1
Значение формулы Байеса состоит
в том, что при
наступлении события А, т.е. по мере получения новой
Доказательство:
информации,
мы можем проверять и корректировать
выдвинутые
доискомой
испытания
гипотезы.
Для получения
формулы
запишем теорему умножения
вероятностей
А и Hi двух
формах:
Такой
подход, событий
называемый
байесовским,
дает возможность корректировать управленческие решения,
A) P( Hоценки
),
i ) P( A) P( H
i ) P( A | H i неизвестных
например, вP( AH
экономике,
аi |также
параметров распределения
изучаемых признаков в
P( H i ) P( A | H i )
откуда Р( H i | A) анализе и т.п.
, и с учетом формулы полной
статистическом
P( A)
вероятности
Р(Н i | A)
P(H i )P(A | H i )
n
P(H )P(A | H )
i 1
i
i
.

20.

ТРЕТИЙ ВОПРОС
Повторные независимые
испытания

21.

Схема Бернулли
Если вероятность наступления события А в каждом испытании
не меняется в зависимости от исходов других, то такие испытания
называются независимыми относительно события А.
Если независимые повторные испытания проводятся при одном
и том же комплексе условий, то вероятность наступления
события А в каждом испытании одна и та же.
Теорема (Формула Бернулли)
Если вероятность р наступления события А в каждом испытании постоянна, то вероятность Рmn того, что событие А наступит
m раз в n независимых испытаниях, равна
Рm,n C p q
m
n
где q = 1 - р.
m
n m
n!
p m q n m ,
m!(n m)!

22.

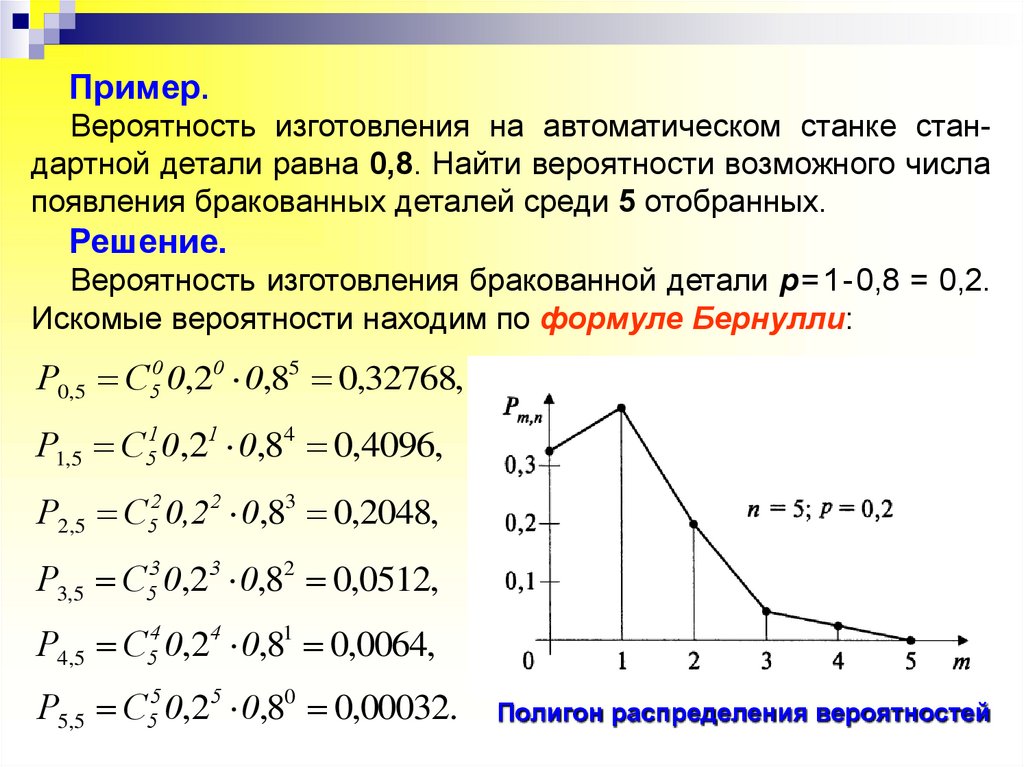
Пример.
Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности возможного числа
появления бракованных деталей среди 5 отобранных.
Решение.
Вероятность изготовления бракованной детали р=1-0,8 = 0,2.
Искомые вероятности находим по формуле Бернулли:
Р0,5 C50 0,20 0,85 0,32768,
Р1,5 C51 0,21 0,84 0,4096,
Р2,5 C52 0,2 2 0,83 0,2048,
Р3,5 C53 0,23 0,82 0,0512,
Р4,5 C54 0,24 0,81 0,0064,
Р5,5 C55 0,25 0,80 0,00032.
Полигон распределения вероятностей

23.

Число m0 наступления события А в n независимых испытаниях
называется наивероятнейшим, если вероятность его осуществления Pm0 , n по крайней мере не меньше вероятностей Pm , n друдругих событий при любом m:
Pm0 n Pm0 1, n ;
Pm0 n Pm0 1, n .
Решим первое неравенство системы, используя формулы
Бернулли и числа сочетаний, запишем:
n!
n!
p m0 q n m0
p m0 1q n m0 1 ,
m0 !(n m0 )!
(m0 1)! (n m0 1)!
преобразовав которое, получим –
m0 np q.
Для второго (аналогично) –
m0 np p.
Окончательно получаем:
np q m0 np p.

24.

Пример.
По данным предыдущего примера найти наивероятнейшее
число появления бракованных деталей из 5 отобранных и
вероятность этого числа.
Решение.
По формуле 5∙0,2 - 0,8 < m0 < 5∙0,2 + 0,2 или 0,2 < m0 < 1,2.
Единственное целое число, удовлетворяющее полученному неравенству, m0 = 1, а его вероятность Р1,5 0,4096.
Пример.
Сколько раз необходимо подбросить игральную кость, чтобы
наивероятнейшее выпадение тройки было равно 10?
Решение.
В данном случае р = 1/6. Согласно неравенству
1 5
1 1
или 59 ≤ n ≤ 65,
n 10 n
6 6
6 6
т.е. необходимо подбросить кость от 59 до 65 раз (включительно).

25.

Теорема Пуассона.
Если вероятность р наступления события А в каждом испытанииПредположим,
стремится к нулю
(р →хотим
0) привычислить
неограниченном
увеличении
что мы
вероятность
Рm,n
числа n испытаний
(n →А∞),при
причем
произведение
стремится n,
к
появления
события
большом
числе np
испытаний
постоянному
например,
Р300числу
,500 . λ (np → λ), то вероятность Рm,n того, что событие А появится m раз в n независимых испытаниях, удовлетПо формуле
Бернулли:
воряет
предельному
равенству
m
500
!
e
300 200
P300,500 lim
C Pp q P ( )
p
q ,
.
300
m! 200!
300 300 500 300
500 m , n
m
n
непосредственное
вычисление
технически сложно,
тем более
Формула Пуассона
для маловероятных
событий.
если
учесть,
что сами рр и—q постоянна
— числа дробные.
Если
вероятность
и мала, число испытаний
n —Простые
велико иприближенные
число λ = nр —
незначительно
(будем полагать,
формулы
для вычисления
Рm,n при
что λ = n
nрформулы,
< 10), тоназываемые
из предельного
равенства вытекает
больших
асимптотическими,
сущеприближенная формула Пуассона:
ствуют и определяются теоремой Пуассона, локальной и
m eМуавра
интегральной теоремами
– Лапласа.
Pm,n
m!
Pm ( ).
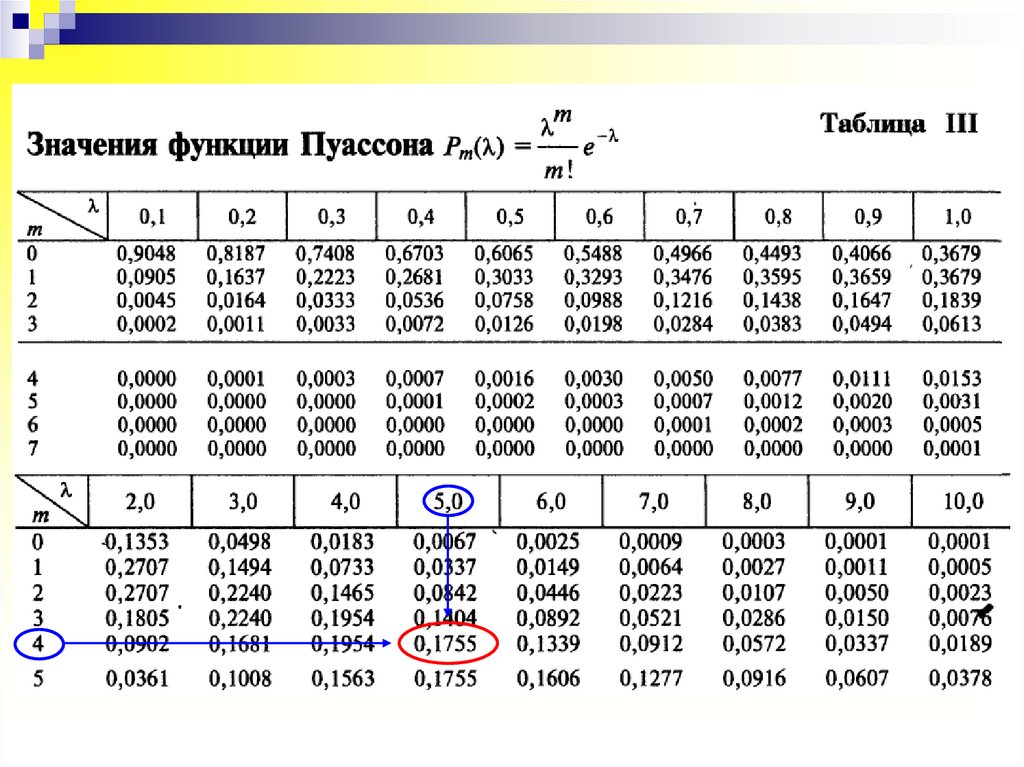
Значения функции Пуассона приведены в табл. III приложений.

26.

Пример.
На факультете насчитывается 1825 студентов.
Какова вероятность того, что 1 сентября является днем
рождения одновременно четырех студентов факультета?
Решение.
Вероятность того, что день рождения студента 1 сентября,
равна р = 1/365.
Так как р = 1/365 — мала,
n = 1825 — велико,
λ = nр = 1825 ∙ (1/365 ) = 5 < 10,
то, применяя формулу Пуассона, по таблице III приложений
получаем:
P4,1825 P4 (5) 0,1755.

27.

Локальная теорема Муавра – Лапласа.
Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Рmn того, что
событие А произойдет m раз в n независимых испытаниях при
достаточно большом числе n, приближенно равна:
где
f ( x)
1
e
2
x2
2
f ( x)
Pm,n
,
npq
– функция Гаусса и x
m np
.
npq
Приближенные значения вероятности Рmn, задаваемые локальной формулой, на практике используются как точные при
условии npq > 20.
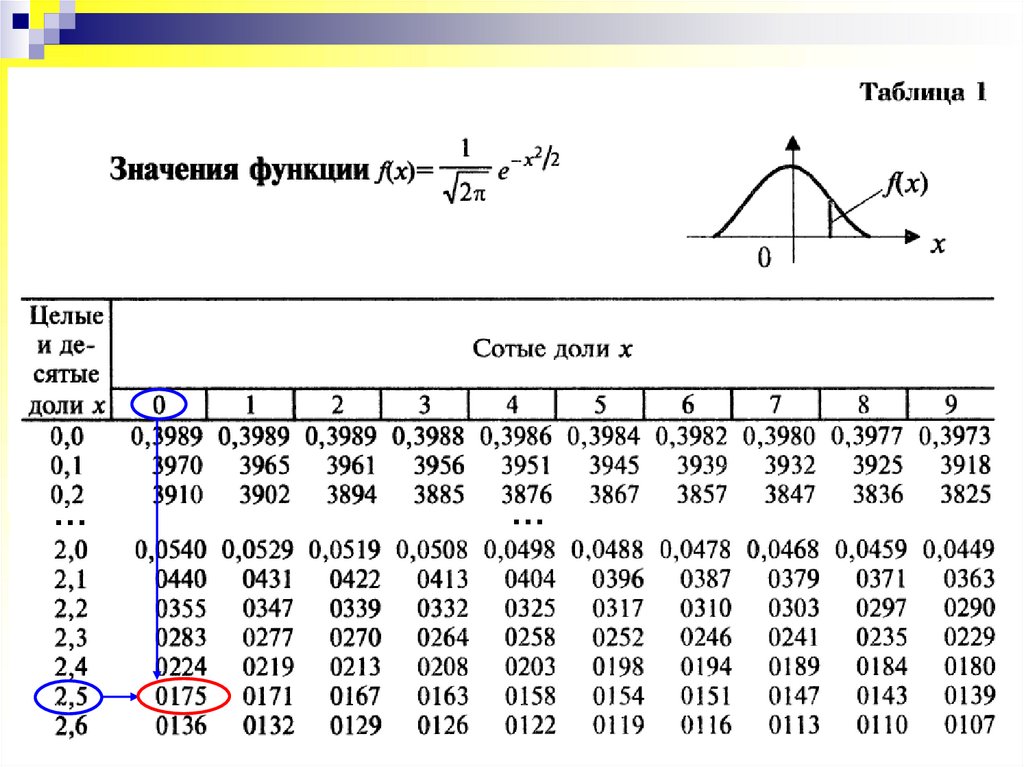
Значения функции Гаусса приведены в табл. I приложений.
1. Функция f(x) является четной, т.е. f(-x) = f(х).
2. Функция f(x) – монотонно убывающая при положительных
значениях х, причем при х → ∞ f(x) → 0 (практически можно
считать, что уже при х > 4 f(x) ≈ 0.

28.

Пример.
В некотором городе из каждых 100 семей 80 имеют
компьютеры. Найти вероятность того, что из 400 семей 300
имеют компьютеры.
Весьма малое значение вероятности Р300,400 не должно
Решение.
вызывать сомнения, так как кроме события «ровно 300
Вероятность того, что в некотором городе семья имеет
семей из 400 имеют компьютеры» возможно еще 400
компьютер, равна р = 80/100 = 0,8.
событий: «0 из 400», «1 из 400»,..., «400 из 400» со своими
Так как
n = 100 достаточно велико,
вероятностями.
npq = 100∙0,8(1—0,8) = 64 > 20,
Все вместе эти события образуют полную группу, а
то применяем локальную формулу Муавра—Лапласа.
значит, сумма их вероятностей равна единице.
…Вначале определим
Тогда
300 400 0,8
x …
2,50.
400 0,8 0,2
f ( 2,50)
f (2,50) 0,0175
P300, 400
0,0022
8
400 0.8 0.2
64
(значение f(2,5) найдено по таблице I приложений).

29.

Интегральная теорема Муавра—Лапласа.
Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число
m При
наступления
А в n независимых
испытаниях заклюрешениисобытия
интервальных
задач, например,
чено в пределах от а до b (включительно), при достаточно большом числе n приближенно равна:
P400 (300 m 350) P300, 400 P301, 400 ... P350, 400
1
b np
a np
Ф
(
)
Ф
(
) ,
вычислить 2 каждое
npq слагаемое
npq
Pn (a m b)
в принципе
можно по
x
t
локальной2 формуле
Муавра – Лапласа, но их большое
2
e dt - функция Лапласа (интеграл вероятностей);
где Ф( x)
количество
расчет весьма громоздким.
2 делает
0
В подобных
используется
интегральная
При
выполнении случаях
условия npq
> 20 интегральная
формула
дает, как правило,
для практики погрештеорема
Муавра удовлетворительную
– Лапласа.
2
ность вычисления вероятностей.
Значения функции Лапласа приведены в табл. II приложений.
1. Функция Ф(x) является нечетной, т.е. Ф(-x) = - Ф(х).
2. Функция Ф(x) – монотонно возрастающая, причем при х → ∞
Ф(x) → 1, практически можно считать, что уже при х > 4 Ф(x) ≈ 1.

30.

Следствия
Пример. .
Если вероятность р наступления события А в каждом испытаВ некотором
100
семей
80 имеют
пернии
постоянна игороде
отличнаизоткаждых
0 и 1, то
при
достаточно
большом
сональные
компьютеры.
Найтивероятность
вероятность
того,
числе n независимых
испытаний
того,
что:что от 280
доа)360
семей
из 400 имеют
компьютеры.
число
m наступлений
события
А отличается от произведения
nрРешение.
не более, чем на величину ε > 0 (по абсолютной величине):
Вычислить вероятность Р400 (280 < m < 360) можно и по
;
Pn m np Ф
Муавра–Лапласа.
основной формуле интегральной теоремы
npq
Ночастость
проще m/n
этособытия
сделать,
если заметить,
б)
А заключена
в пределахчто
от αграницы
до β
интервала
280 и 360 симметричны относительно величины
(включительно):
p
m
1 p
nр = 320, где р = 0,8.
;
Pn Ф
Ф
pq n
n
Тогда по формуле следствия
а)2 pq n
P400 (280
m
360) А Pотличается
320
40)
в) частость
m /n
события
его вероятности
р
400 ( 40 mот
не более, чем на величину Δ > 0 (по абсолютной величине):
40
P400 ( m 320 40m)
n (5,0) 1.
0 ,8 0,2 .
Pn
p 400
Ф
n
pq

31.

Благодарю за внимание,
лекция окончена!