Предельные теоремы теории вероятностей

1.

Предельные теоремы
теории вероятностей
1

2. Можно ли установить закономерность совокупного поведения случайных величин?

При
некоторых,
достаточно
широких
условиях,
суммарное
поведение большого числа случайных
величин
утрачивает
случайный
характер и становится закономерным.
2

3. Центральные предельные теоремы (Ц.П.Т.)

Ц.П.Т.— класс теорем в теории
вероятностей, утверждающих, что
сумма достаточно большого
количества слабо зависимых
случайных величин, имеющих примерно
одинаковые масштабы (ни одно из
слагаемых не доминирует, не вносит в
сумму определяющего вклада), имеет
распределение, близкое к нормальному
3

4. Зако́н больши́х чи́сел

в теории вероятностей утверждает, что
эмпирическое среднее (среднее
арифметическое) достаточно большой
конечной выборки из фиксированного
распределения близко к теоретическому
среднему (математическому ожиданию)
этого распределения.
4

5. Чебышев Пафнутий Львович

Предельные теоремы теории вероятностей
Чебышев Пафнутий Львович
1821-1894
Русский математик и механик.
Написал более 70 работ по теории
чисел, теории вероятностей, теории
приближения
функций,
интегральному
исчислению,
теории
механизмов.
Доказал
достаточно
общие формы закона больших чисел.
Доказанная
им
центральная
предельная
теорема,
а
также
исследования
его
учеников
А.А.Маркова и А.М. Ляпунова стали
основой русской школы теории
вероятностей.
5

6. Марков Андрей Андреевич Марков Андрей Андреевич Марков Андрей Андреевич

Предельные теоремы теории вероятностей
Марков Андрей Андреевич
1856-1922
Русский математик.
Написал около 70 работ по
теории
чисел,
теории
приближения функций, теории
вероятностей. Существенно расширил сферу применения закона
больших чисел и центральной
предельной теоремы. Является
основоположником теории случайных процессов.
6

7. Первое неравенство Чебышева (неравенство Маркова)

Предельные теоремы теории вероятностей
Первое неравенство Чебышева
(неравенство Маркова)
Для каждой неотрицательной
случайной величины , имеющей
математическое ожидание M [ ] ,
при любом 0
справедливо
М [ ]
P{ }
.
7

8. Первое неравенство Чебышева ПРИМЕР

Предельные теоремы теории вероятностей
Первое неравенство Чебышева
ПРИМЕР
►Пусть - время опоздания
студентов на лекцию. Известно,
M [ ] =1
что
мин.
Оценить
вероятность того, что студент
опоздает не менее чем на 5 минут.
М [ ]
P{ }
☻
,
1
P{ 5} ◄
5
8

9. Первое неравенство Чебышева ПРИМЕР

Предельные теоремы теории вероятностей
Первое неравенство Чебышева
ПРИМЕР
►Среднее
число
вызовов,
поступающих
на
коммутатор
в
течение часа, равно 300. Оценить
вероятность того, что в течение
следующего часа число вызовов
будет не более 500.
М [ ]
М [ ]
P{ } 1
☻ P{ }
300
M [ ] 300 , P{ 500} 1
0.4
500
Вероятность не менее 0.4 ◄
9

10. Второе неравенство Чебышева

Предельные теоремы теории вероятностей
Второе неравенство Чебышева
Для
каждой
случайной
величины
имеющей
,
дисперсию
при
D[ ] 2 ,
любом 0 справедливо
2
P{ M [ ] } 2 .
10

11. Второе неравенство Чебышева ПРИМЕР

Предельные теоремы теории вероятностей
Второе неравенство Чебышева
ПРИМЕР
►Средний расход воды на ферме составляет 1000 л в день,
а среднее квадратичное =200 л. Оценить вероятность того,
что расход воды в любой выбранный день не превысит 2000 л.
☻ Т.к. границы интервала 0 2000 симметричны
относительно M [ ] 1000 и
P{ 2000} P{0 2000} P{ 1000 1000},
тогда, учитывая
2
2
P{ M [ ] } 2 P{ M [ ] } 1 2
получим
2002
P{ 1000 1000} 1
0.96 ◄
2
1000
11

12. Закон больших чисел

Предельные теоремы теории вероятностей
Закон больших чисел
Закон больших чисел - это ряд теорем, которые
доказывают
устойчивость
средних
1 2 ... n
арифметических случайных величин
:
n
при большом количестве испытаний n они
перестают быть случайными и стремятся к
некоторым постоянным.
12

13. Марков Андрей Андреевич Марков Андрей Андреевич Пуассон Симеон Дени

Предельные теоремы теории вероятностей
Пуассон Симеон Дени
1781-1840
Французский механик, физик, математик.
Написал свыше 350 работ в
области
небесной
механики,
механики, определенных интегралов, дифференциальных уравнений, рядов, теории вероятностей, статистики.
Ввел термин «закон больших
чисел» (1837 г.).
13

14. Среднее двух случайных величин

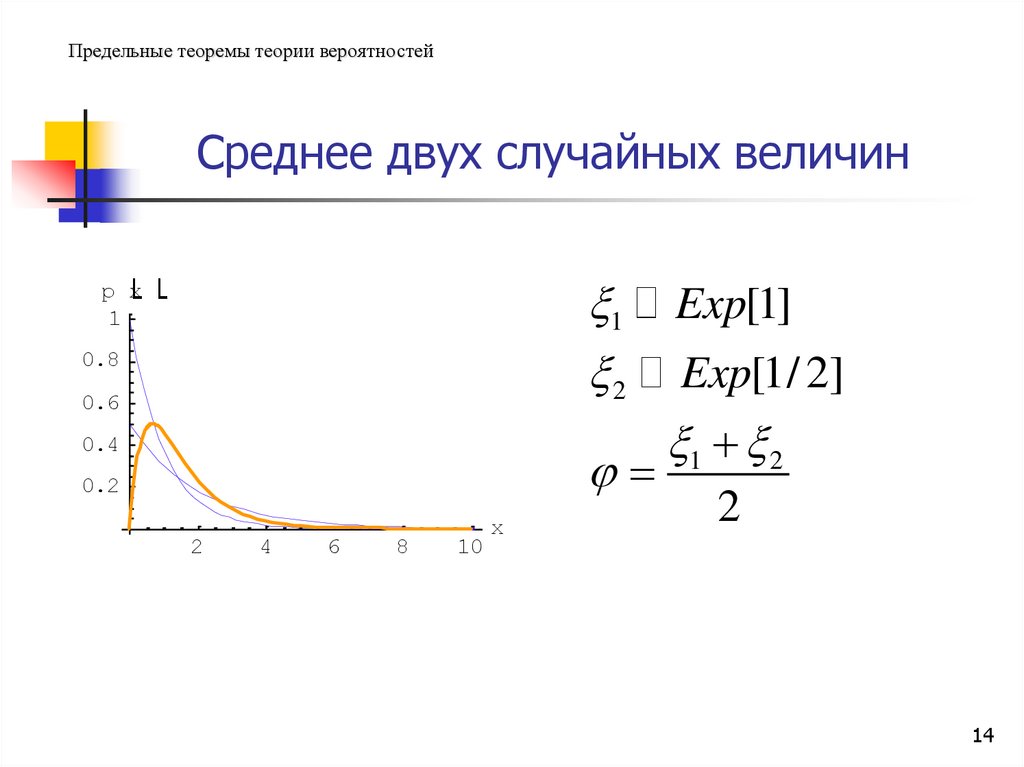
Предельные теоремы теории вероятностей
Среднее двух случайных величин
1
2
p x
1
0.8
0.6
0.4
0.2
2
4
6
8
10
x
Exp[1]
Exp[1/ 2]
1 2
2
14

15. Среднее пяти случайных величин

Предельные теоремы теории вероятностей
Среднее пяти случайных величин
1 Exp[1/ 2] M [ 1 ] 2
2 Exp[1/ 3] M [ 2 ] 3
3 Exp[1/ 4] M [ 3 ] 4
4 Exp[1/ 5] M [ 4 ] 5
5 Exp[1/ 6] M [ 5 ] 6
p x
0.5
0.4
0.3
0.2
0.1
2
4
6
8 10 12 14
x
D[ 1 ] 4
D[ 2 ] 9
D[ 3 ] 16
D[ 4 ] 25
D[ 5 ] 36
1 5
M [ i ] 4
5 i 1
1 5
i
5 i 1
M [ ] 4 D[ ] 3.6
15

16. Сущность закона больших чисел

Предельные теоремы теории вероятностей
Сущность закона больших чисел
Есть независимые случайные величины, каждая из
которых может принимать значения, далекие от своего
математического
ожидания.
Но
если
мы
их
просуммируем, то среднее арифметическое достаточно
большого числа случайных величин с большой
вероятностью
принимает
значения,
близкие
к
определенному неслучайному постоянному числу т.е.
значения отдельных случайных величин могут иметь
большой разброс, а их среднее арифметическое малый.
16

17. Теорема Чебышева

Предельные теоремы теории вероятностей
Теорема Чебышева
Если 1 , 2 , n – независимые случайные величины,
для которых существуют M [ i ] mi и D[ i ] i2 , причем
дисперсии их не превышают некоторой константы C, то,
как бы мало не было 0 ,
1 2 ... n m1 m2 ... mn
P
1
n
n
n
17

18. Доказательство теоремы Чебышева

Предельные теоремы теории вероятностей
Доказательство теоремы Чебышева
1 n
1 n
1 n
1 n 2 Cn C
M [ i ] mi , D[ i ] 2 i 2
n i 1
n i 1
n i 1
n i 1
n
n
Применим второе неравенство Чебышева к
случайной величине
P n M [ n ] 1
1 n
n i :
n i 1
D[ n ]
2
.
C
1 n
Т.к. M [ i ] mi и D[ i ] :
n
n i 1
1 ... n m1 ... mn
C
P
1 2 1 при n ■
n
n
n
18

19. Следствие теоремы Чебышева

Предельные теоремы теории вероятностей
Следствие теоремы Чебышева
Если 1 , 2 , …, n , … – независимые случайные
M [ i ] m
величины,
имеющие
одинаковые
и
ограниченные дисперсии, то, как бы мало не было 0 ,
1 2 ... n
P
m
1.
n
n
19

20. Следствие теоремы Чебышева. Пример.

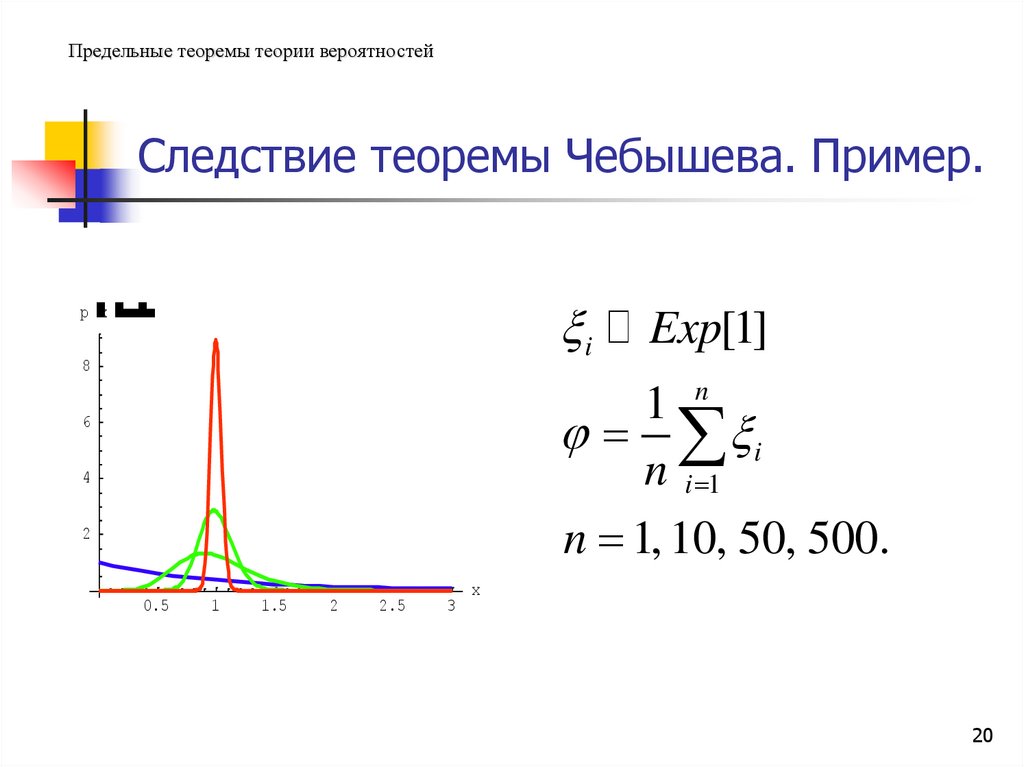
Предельные теоремы теории вероятностей
Следствие теоремы Чебышева. Пример.
HL
i
p x
8
Exp[1]
1 n
i
n i 1
n 1, 10, 50, 500.
6
4
2
0.5
1
1.5
2
2.5
3
x
20

21. Практическое значение теоремы Чебышева. ПРИМЕР.

Предельные теоремы теории вероятностей
Практическое значение теоремы Чебышева.
ПРИМЕР.
Страховой компании необходимо установить
размер страхового взноса.
Рассматривая убытки, как случайные величины, и
обладая статистикой, можно определить средние
убытки, которые на основании теоремы Чебышева
можно считать величиной почти не случайной.
Тогда на основании этих данных и предполагаемой
страховой суммы определяется размер страхового
взноса.
21

22. Практическое значение теоремы Чебышева. ПРИМЕР.

Предельные теоремы теории вероятностей
Практическое значение теоремы Чебышева.
ПРИМЕР.
При измерении некоторой физической величины,
истинное значение которой равно m , проводят n
независимых измерений этой величины. Результат
каждого измерения – случайная величина i . Если при
измерениях
отсутствуют
систематические
погрешности, то на основании следствия из теоремы
1 2 ... n
m при n .
Чебышева
n
22

23. Практическое значение теоремы Чебышева. ПРИМЕР.

Предельные теоремы теории вероятностей
Практическое значение теоремы Чебышева.
ПРИМЕР.
Если все измерения проводятся с одинаковой
точностью 2 , то дисперсия их средней
1 2 ... n 1
D
2 D 1 2 ... n
n
n
1
2
2 ( D[ 1 ] D[ 2 ] ... D[ n ])
.
n
n
Т.о., увеличивая число измерений,
увеличивать точность измерений.
можно
23

24. Якоб Бернулли 1654 - 1705

Предельные теоремы теории вероятностей
Якоб Бернулли 1654 - 1705
Швейцарский математик.
Наиболее
значительны
достижения в развитии анализа
бесконечно малых, теории рядов,
вариационного исчислении и
теории вероятностей. Благодаря
его работам теория вероятностей
приобрела важнейшее значение в
практической деятельности.
24

25. Теорема Бернулли

Предельные теоремы теории вероятностей
Теорема Бернулли
Пусть проводится n испытаний по схеме
Бернулли и m – общее число успехов. Тогда
справедливо
m
lim P{ p } 1,
n
n
где p – вероятность успеха в одном испытании.
25

26. Теорема Бернулли

Предельные теоремы теории вероятностей
Теорема Бернулли
Теорема Бернулли – следствие теоремы Чебышева, т.к.
m
статистическую вероятность события
можно
n
представить как среднее арифметическое n независимых
случайных величин , имеющих одинаковый закон
1
распределения: .
n
26

27. Теорема Бернулли

Предельные теоремы теории вероятностей
Теорема Бернулли
Теорема Бернулли дает теоретическое обоснование
его
события
вероятности
неизвестной
замены
статистической вероятностью, утверждая, что при n
статистическая вероятность стремиться по вероятности
к постоянной вероятности события:
P
m
p
n
n
27

28. Центральная предельная теорема

Предельные теоремы теории вероятностей
Центральная предельная теорема
Ц.П.Т. – это ряд теорем, в которых рассматривается
вопрос о законе распределения суммы взаимно
независимых случайных величин при неограниченном
увеличении числа слагаемых. При некоторых весьма
общих условиях закон распределения суммы случайных
величин приближается к нормальному. Установление
таких условий и составляет содержание теоремы.
28

29. Сущность Ц.П.Т.

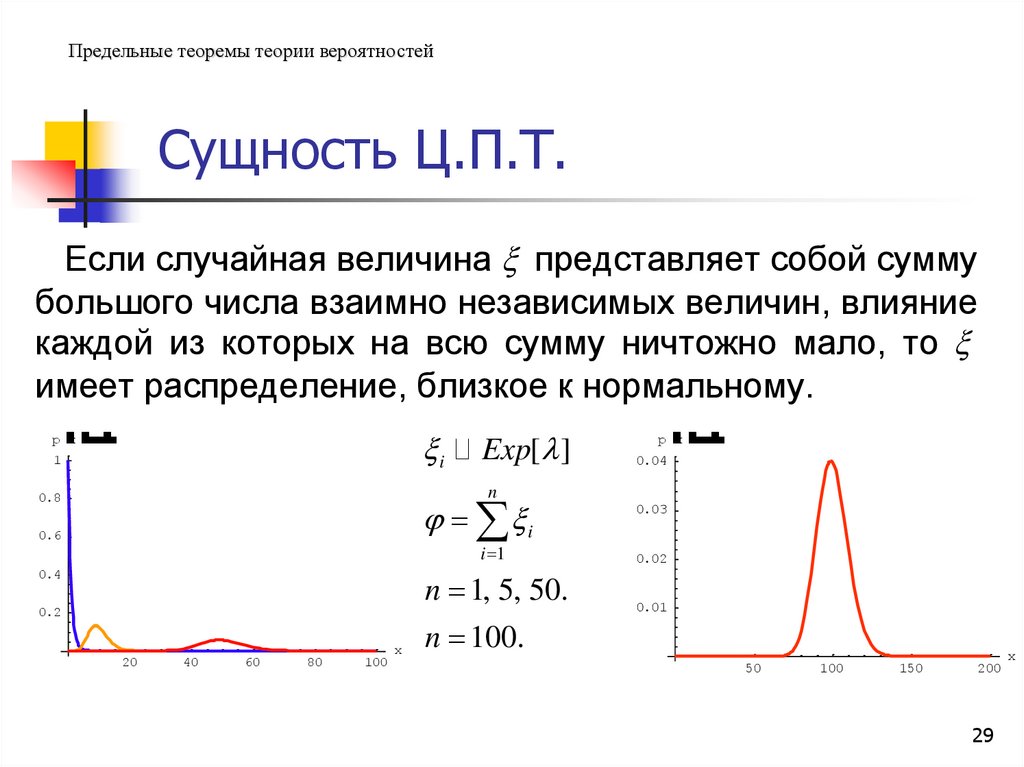
Предельные теоремы теории вероятностей
Сущность Ц.П.Т.
Если случайная величина представляет собой сумму
большого числа взаимно независимых величин, влияние
каждой из которых на всю сумму ничтожно мало, то
имеет распределение, близкое к нормальному.
H
L
i
p x
1
Exp[ ]
H
L
p x
0.04
n
i
0.8
0.6
i 1
0.4
n 1, 5, 50.
0.2
20
40
60
80
100
x
0.03
0.02
0.01
n 100.
50
100
150
200
29
x

30. Ляпунов Александр Михайлович

Предельные теоремы теории вероятностей
Ляпунов Александр Михайлович
1857-1918
Русский математик и механик.
Исследовал проблемы устойматериальных
движения
чивости
предложенные
Методы,
систем.
Ляпуновым применяются во многих
разделах теории дифференциальных
уравнений.. Дал простое и строгое
прецентральной
доказательство
дельной теоремы в общем виде. Для
метод
разработал
доказательства
характеристических функций, котов
применяется
широко
рый
современной теории вероятностей.
30

31. Практическое значение Ц.П.Т. ПРИМЕР.

Предельные теоремы теории вероятностей
Практическое значение Ц.П.Т. ПРИМЕР.
Пусть производится измерение некоторой физической
величины.
Каждое
из
измерений
является
приблизительным, на него влияют многие факторы –
температура, колебания прибора, влажность и т.д.
Каждый из факторов порождает ничтожно малую
ошибку, но совокупность факторов – заметную
суммарную ошибку. Рассматривая суммарную ошибку
как сумму очень большого числа взаимно независимых
случайных величин, можно заключить, что ошибка имеет
нормальное
распределение.
На
этом
строится
статистическое оценивание погрешности.
31

32. Теорема Ляпунова.

Предельные теоремы теории вероятностей
Теорема Ляпунова.
Если 1 , 2 , …, n , …, –независимые случайные
величины, для которых существуют M [ i ] mi и
D[ i ] i2 , абсолютный центральный момент третьего
порядка M [ i mi ] i и
3
n
i 1
lim
n
i
n 2
i
i 1
то закон распределения
приближается
ожиданием
к
n
m
i 1
i
3
2
(♣)
0
n
i 1
i
при n неограниченно
нормальному
и дисперсией
с
математическим
n
i 1
2
i
.
32

33. Теорема Ляпунова.

Предельные теоремы теории вероятностей
Теорема Ляпунова.
Смысл условия (♣) состоит в том, чтобы в сумме
n
i 1
i
не было слагаемых, влияние которых на разброс
подавляюще велико по сравнению с остальными и не
должно быть большого числа слагаемых, влияние
которых очень мало. Т.о. удельный вес каждого
отдельного слагаемого должен стремиться к нулю при
увеличении числа слагаемых.
33

34. Теорема Ляпунова. Пример.

Предельные теоремы теории вероятностей
Теорема Ляпунова. Пример.
Потребление электроэнергии за месяц в каждой
квартире можно представить как n случайных величин.
Если потребление электроэнергии в каждой квартире
резко не выделяется среди остальных, то на основании
теоремы Ляпунова можно считать, что потребление
энергии всего дома будет случайной величиной,
закон
нормальный
приближенно
имеющей
распределения.
Но если в одной из квартир находится прачечная, то
вывод о приближенно нормальной энергии всего дома
будет неправомерен.
34

35. Следствие теоремы Ляпунова.

Предельные теоремы теории вероятностей
Следствие теоремы Ляпунова.
Если все случайные величины i
одинаково распределены с D[ i ] 2 , то
закон
при
n
приближается
к
распределения
неограниченно
нормальному.
n
i 1
i
35

36. Теорема Ляпунова. Пример.

Предельные теоремы теории вероятностей
Теорема Ляпунова. Пример.
Моделирование нормального распределения
p x
i
1
0.8
R[0,1]
n
i
0.6
n 1, 2, 3, 6.
i 1
0.4
i 6
0.2
1
2
3
4
5
6
x
n n
N[ ,
]
2 12
36

37. Муавр Абрахам

Предельные теоремы теории вероятностей
←
п
р
е
д
ы
д
у
щ
а
я
Муавр Абрахам
1667-1754
Английский математик.
Труды по теории рядов, теории
вероятностей, теории комплексных
чисел. В теории вероятностей
предельную
важную
доказал
теории
В
(1730).
теорему
комплексных чисел вывел правила
возведения в степень и извлечения
корней.
37

38. Лаплас Пьер Симон

Предельные теоремы теории вероятностей
←
п
р
е
д
ы
д
у
щ
а
я
Лаплас Пьер Симон
1749-1827
Французский математик, физик и
астроном.
Фундаментальные работы по
математике, экспериментальной и
математической
физике
и
небесной механике. Является
одним из создателей теории
вероятностей. Доказал важную
предельную теорему. , развил
теорию ошибок. Ввел теоремы
сложения и умножения вероятностей, понятия производящих
функций
и
математического
ожидания.
38

39. Ц.П.Т. Биномиальное распределение.

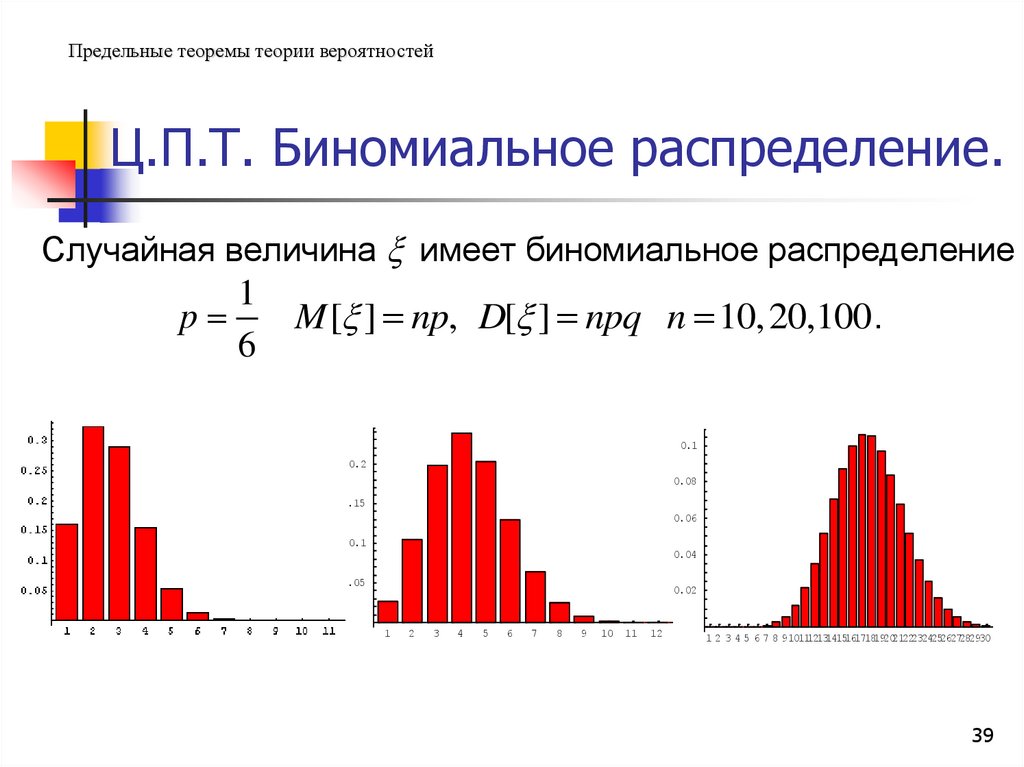
Предельные теоремы теории вероятностей
Ц.П.Т. Биномиальное распределение.
Случайная величина имеет биномиальное распределение
1
p
6
M [ ] np, D[ ] npq n 10, 20,100.
0.1
0.2
0.08
0.15
0.06
0.1
0.04
0.05
0.02
1
2
3
4
5
6
7
8
9
10
11
12
1 2 3 4 5 6 7 8 9101112131415161718192021222324252627282930
39

40. Локальная теорема Муавра-Лапласа.

Предельные теоремы теории вероятностей
Локальная теорема Муавра-Лапласа.
Если в схеме Бернулли число
испытаний
велико,
то
n
вероятность того, что событие A
появится ровно k раз
1
Pn (k )
* ( x) ,
npq
где
x
k np
,
( x)
1
*e
x2
2
-
2
плотность
стандартного
нормального распределения.
npq
40

41. Локальная теорема Муавра-Лапласа. Пример.

Предельные теоремы теории вероятностей
Локальная теорема Муавра-Лапласа. Пример.
►Вероятность попадания в цель при одном выстреле
равна 0.8. Определить вероятность того, что из 400
выстрелов будет ровно 300 попаданий в цель.
1
k np
* (
),
☻ n вполне велико: Pn (k )
npq
npq
npq 400*0.2*0.8 8,
300 320
x
2.5 ,
8
1
1
0.175
P400 (k 300) * ( 2.5) * (2.5)
0.022 ◄
8
8
8
41

42. Интегральная теорема Муавра-Лапласа.

Предельные теоремы теории вероятностей
Интегральная теорема Муавра-Лапласа.
Если в схеме Бернулли число испытаний n велико, то
вероятность того, что событие A появится в испытаниях
от k1 до k 2 раз, приближённо равна
Pn (k1 k k2 ) 0 ( x2 ) 0 ( x1 ) ,
k1 np
k2 np
где x1
, x2
.
npq
npq
x
0 ( x) ( y )dy
0
1
x
e
2
y2
2
dy - интеграл Лапласа.
0
42

43. Интегральная теорема Муавра-Лапласа. Пример.

Предельные теоремы теории вероятностей
Интегральная теорема Муавра-Лапласа.
Пример.
► Определить вероятность того, что при 600
бросаниях игральной кости выпадает от 90 до 120 раз
шестерка.
1
☻ n =600, k1=90, k 2 =120, p .
6
90 600*1/ 6
x1
1.1
600*1/ 6*5 / 6
120 600 *1/ 6
x2
2.19
600 *1/ 6 *5 / 6
P600 (90 k 120)= 0 (2,19) - 0 (-1,1)=
◄
= 0 (2,19) + 0 (1,1)=0,486+0,364=0,85.
43