Similar presentations:
Признаки параллельности двух прямых
1.
Классная работаГеометрия
Тема урока: Признаки
параллельности двух прямых
2.
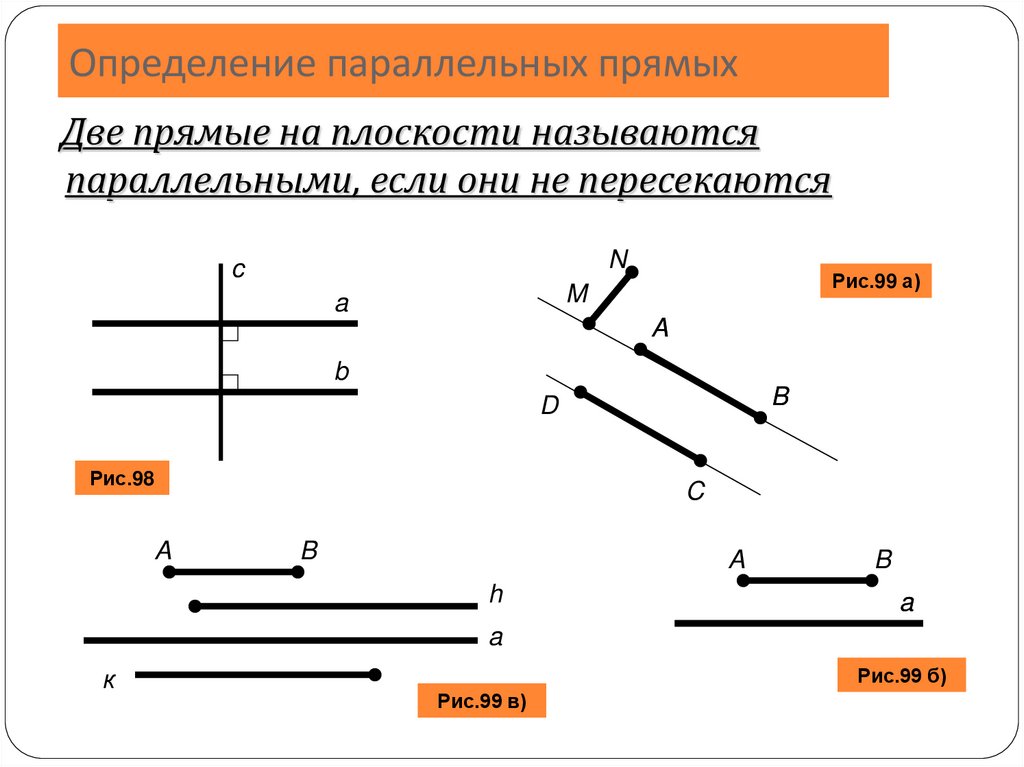
Определение параллельных прямыхДве прямые на плоскости называются
параллельными, если они не пересекаются
N
c
Рис.99 а)
M
a
A
b
B
D
Рис.98
A
C
B
A
h
B
a
a
к
Рис.99 б)
Рис.99 в)
3.
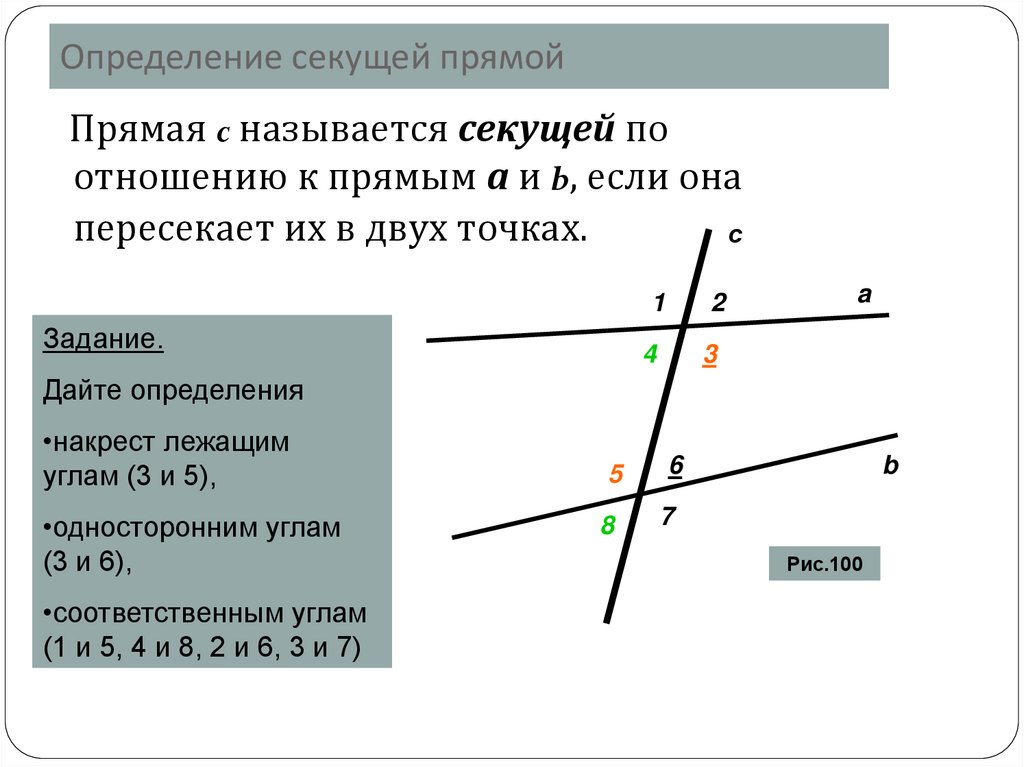
Определение секущей прямойПрямая c называется секущей по
отношению к прямым а и b, если она
пересекает их в двух точках.
с
Задание.
1
2
4
3
a
Дайте определения
•накрест лежащим
углам (3 и 5),
•односторонним углам
(3 и 6),
•соответственным углам
(1 и 5, 4 и 8, 2 и 6, 3 и 7)
5
6
8
7
b
Рис.100
4.
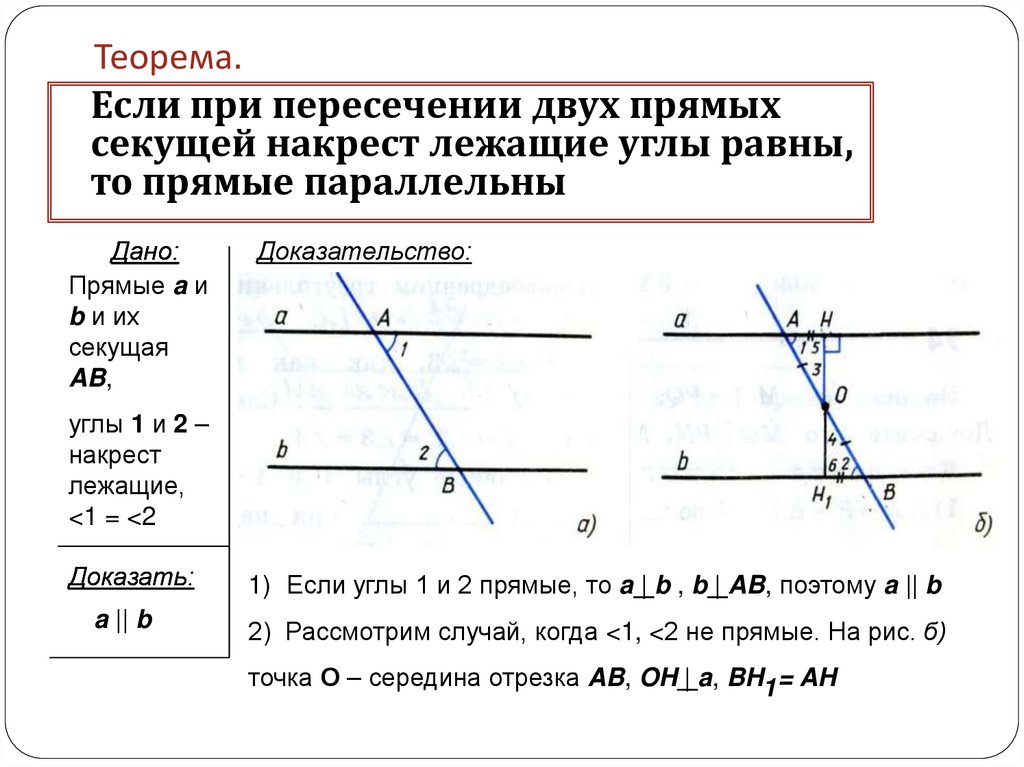
Теорема.Если при пересечении двух прямых
секущей накрест лежащие углы равны,
то прямые параллельны
Дано:
Прямые a и
b и их
секущая
AB,
Доказательство:
углы 1 и 2 –
накрест
лежащие,
<1 = <2
Доказать:
1) Если углы 1 и 2 прямые, то a | b , b | AB, поэтому a || b
a || b
2) Рассмотрим случай, когда <1, <2 не прямые. На рис. б)
точка О – середина отрезка AB, OH | a, BH1 = AH
5.
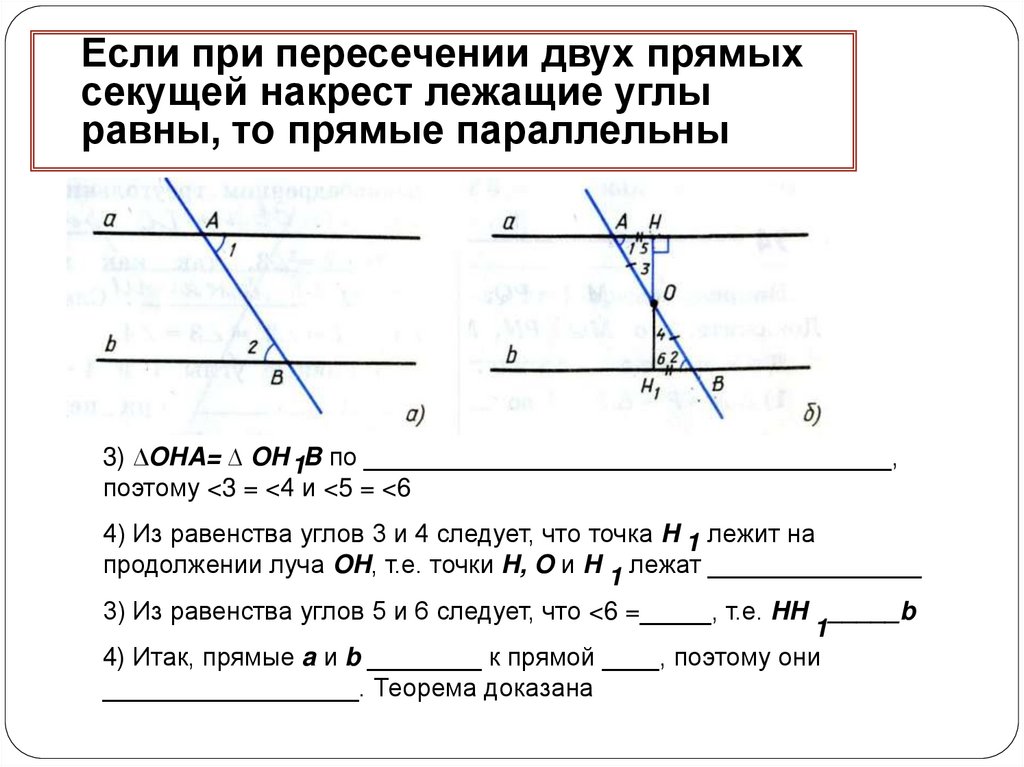
Если при пересечении двух прямыхсекущей накрест лежащие углы
равны, то прямые параллельны
3) ∆OHA= ∆ OH 1B по _____________________________________,
поэтому <3 = <4 и <5 = <6
4) Из равенства углов 3 и 4 следует, что точка H 1 лежит на
продолжении луча OH, т.е. точки H, O и H 1 лежат _______________
3) Из равенства углов 5 и 6 следует, что <6 =_____, т.е. HH _____b
1
4) Итак, прямые a и b ________ к прямой ____, поэтому они
__________________. Теорема доказана
6.
Теорема.Если при пересечении двух прямых
секущей соответственные углы
равны, то прямые параллельны
Дано:
Прямые a и
b и их
секущая
AB,
1) <1 = <2 по
____________________,
углы 1 и 2 –
соответстве
нные,
<2 = <3 , т.к. эти углы
____________,
следовательно, <1 = <3
Доказательство:
<1 = <2
Доказать:
a || b
2) Равные углы 1 и 3 __________________________________________,
поэтому a || b. Теорема доказана.
7.
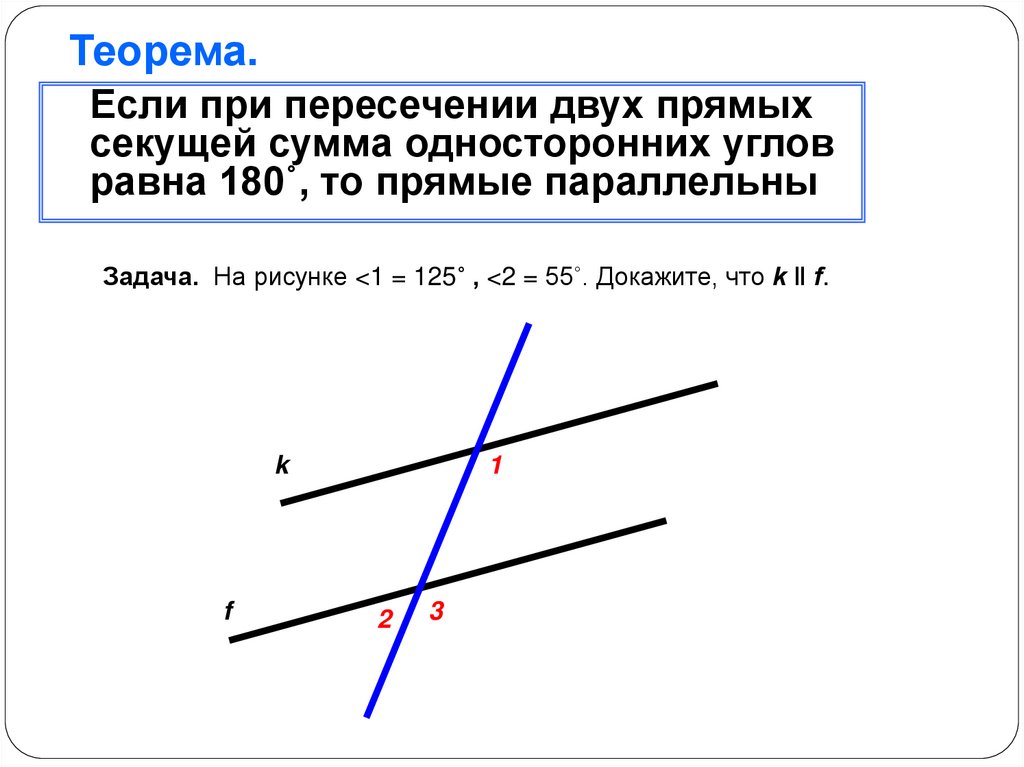
Теорема.Если при пересечении двух прямых
секущей сумма односторонних углов
равна 180˚, то прямые параллельны
Задача. На рисунке <1 = 125˚ , <2 = 55˚. Докажите, что k ‖ f.
k
f
1
2
3
8.
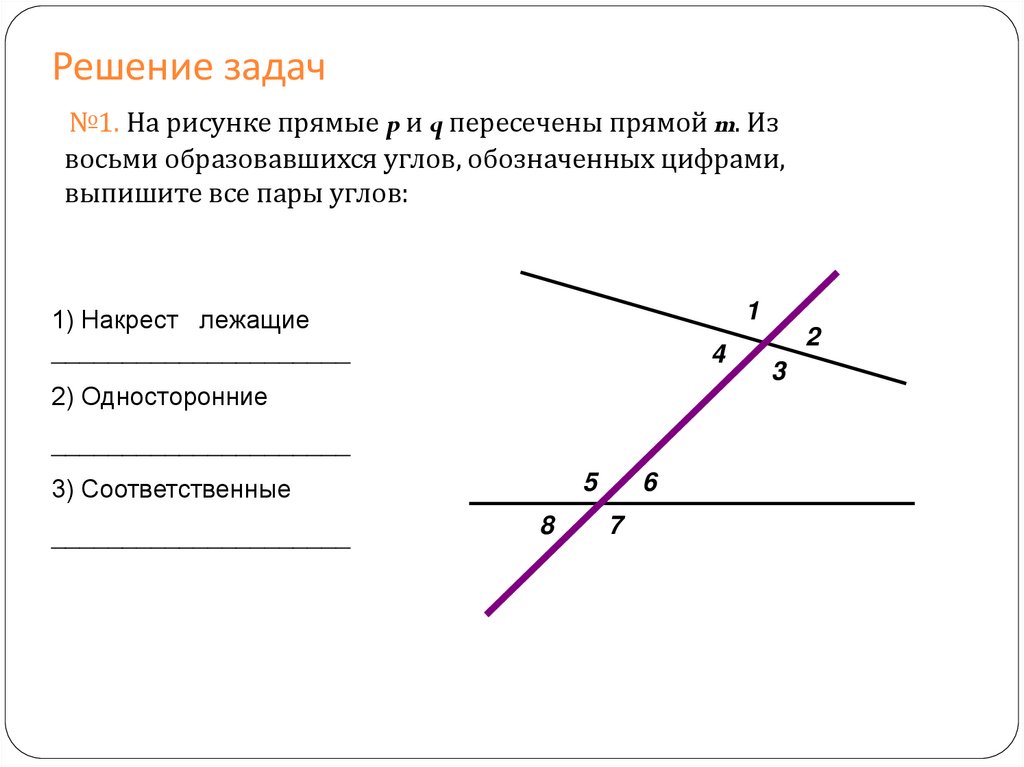
Решение задач№1. На рисунке прямые p и q пересечены прямой m. Из
восьми образовавшихся углов, обозначенных цифрами,
выпишите все пары углов:
1
1) Накрест лежащие
_____________________
4
2) Односторонние
_____________________
5
3) Соответственные
_____________________
8
6
7
2
3
9.
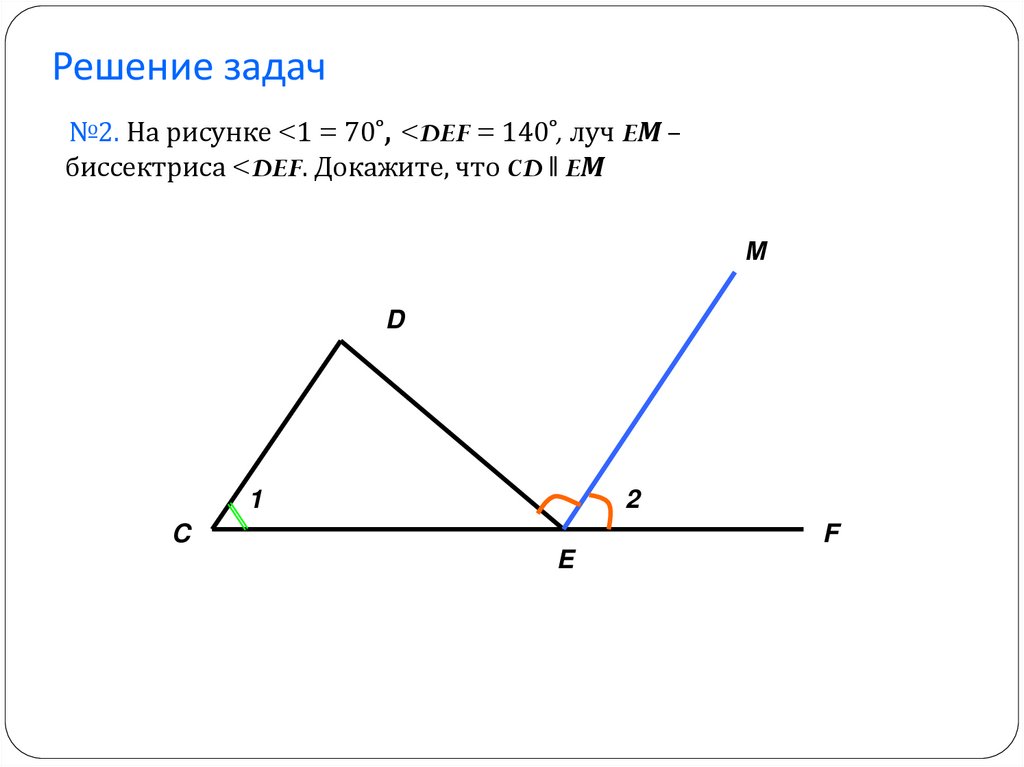
Решение задач№2. На рисунке <1 = 70˚, <DEF = 140˚, луч EМ –
биссектриса <DEF. Докажите, что CD ‖ EМ
М
D
1
2
C
F
E
10.
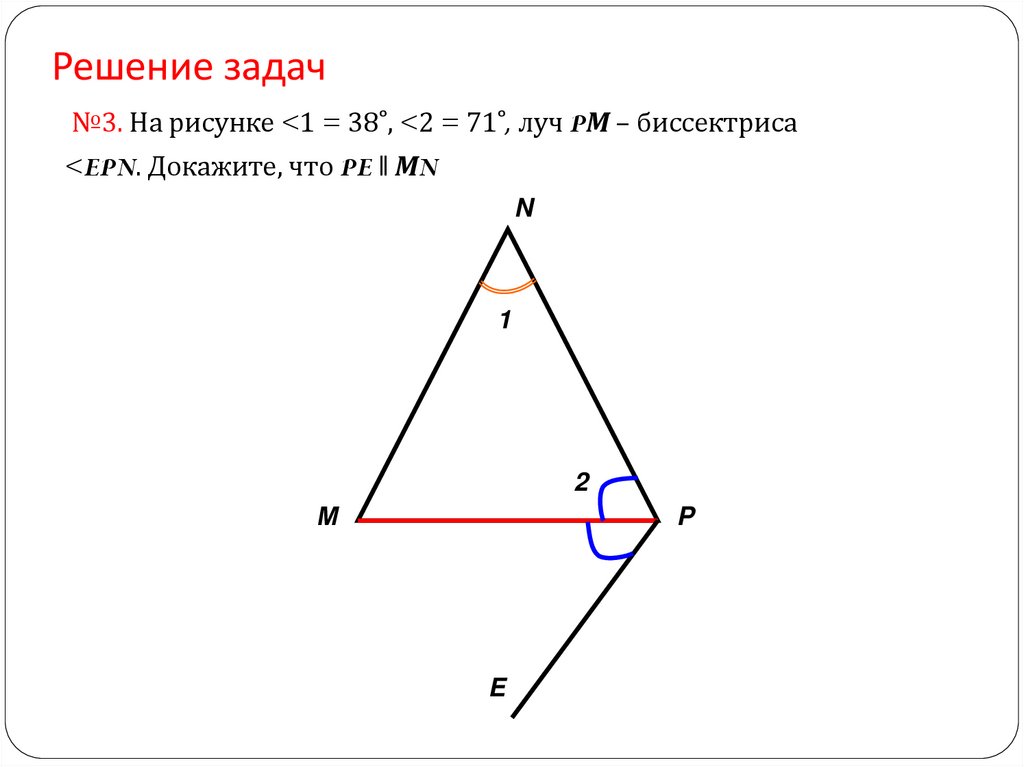
Решение задач№3. На рисунке <1 = 38˚, <2 = 71˚, луч PМ – биссектриса
<EPN. Докажите, что PE ‖ МN
N
1
2
М
P
E
11.
Домашнее задание1.
2.
Выучить 3 теоремы с доказательствами.
По учебнику № 186, 187, 188
12.
Список литературы1)
2)
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э.Г.,
Юдина И.И. Геометрия: учеб. Для 7-9 кл. общеобразоват.
учреждений. – 6 изд. - М.: Просвещение, 1996. – 335 с.
Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И.И.
Рабочая тетрадь для 7 класса общеобразовательных
учреждений - М.: Просвещение, 2004. – 63 с.




 mathematics
mathematics








