Similar presentations:
Признаки параллельности двух прямых
1.
2.
Определение.Две прямые на плоскости называются параллельными,
если они не пересекаются.
3.
Определение.Две прямые на плоскости называются параллельными,
если они не пересекаются.
а
b
аIIb
4.
Две прямые, перпендикулярные к третьей, параллельны.b
c
bIIc
a
5.
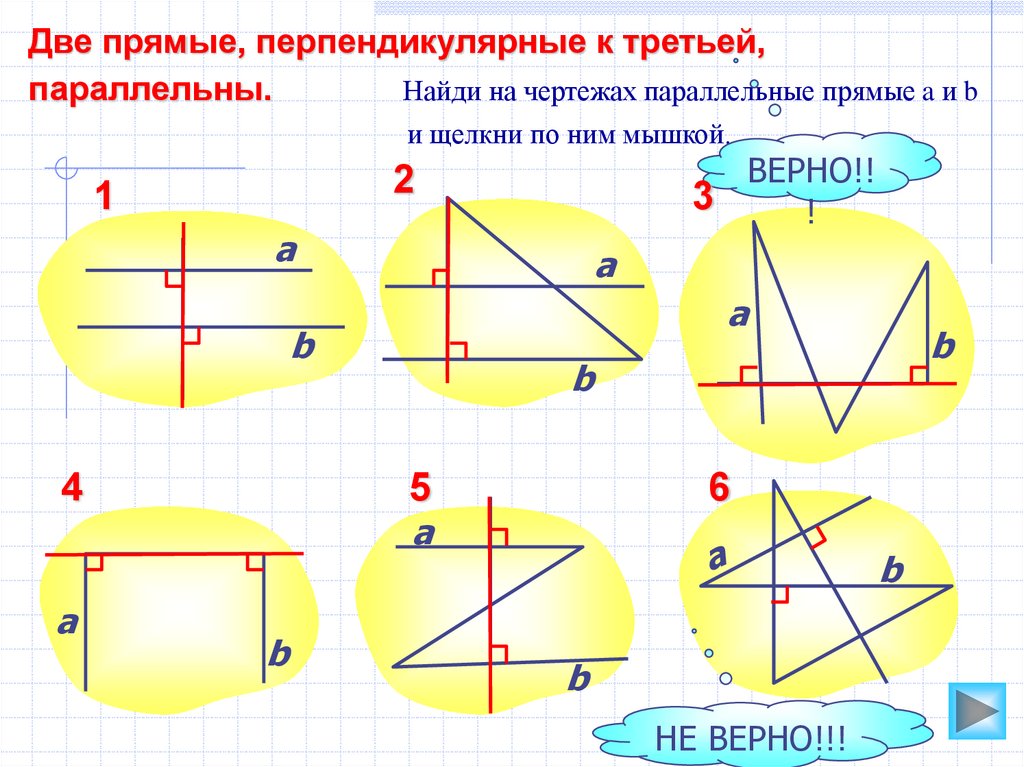
Две прямые, перпендикулярные к третьей,параллельны.
Найди на чертежах параллельные прямые a и b
и щелкни по ним мышкой.
ВЕРНО!!
3
!
2
1
а
а
а
b
4
а
b
5
6
а
b
b
b
b
НЕ ВЕРНО!!!
6.
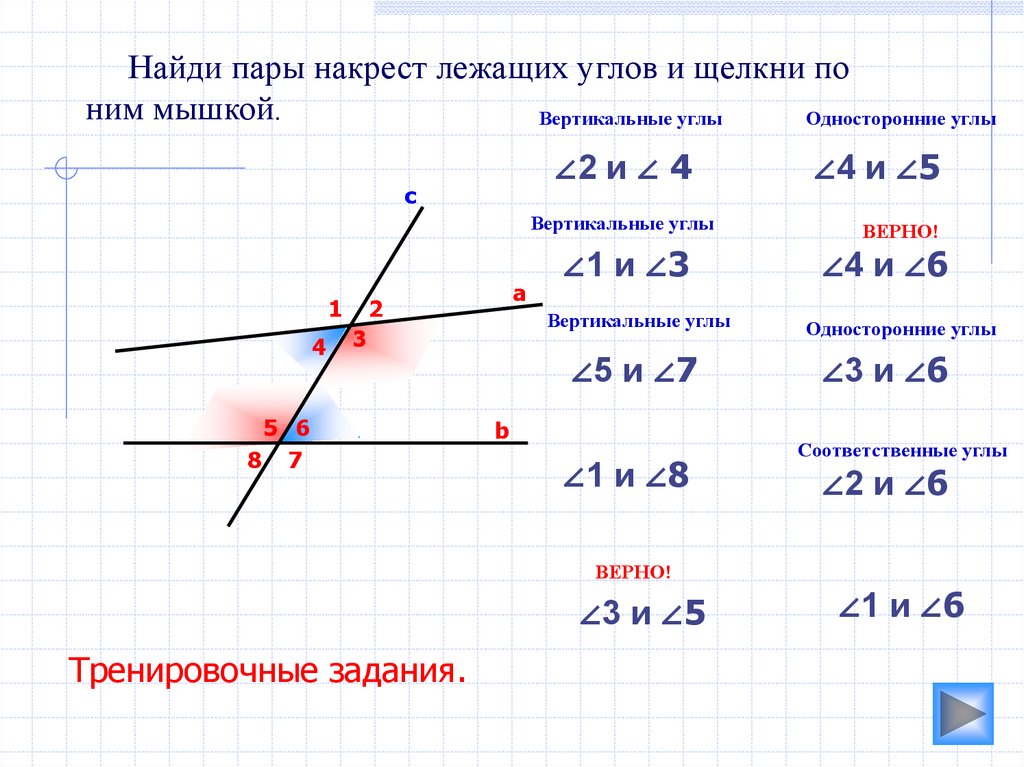
Найди пары накрест лежащих углов и щелкни поним мышкой.
Вертикальные углы
Односторонние углы
∠2 и ∠ 4
c
Вертикальные углы
1
4
а
2
Вертикальные углы
3
5 6
8 7
∠1 и ∠3
∠5 и ∠7
b
∠1 и ∠8
ВЕРНО!
∠3 и ∠5
Тренировочные задания.
∠4 и ∠5
ВЕРНО!
∠4 и ∠6
Односторонние углы
∠3 и ∠6
Соответственные углы
∠2 и ∠6
∠1 и ∠6
7.
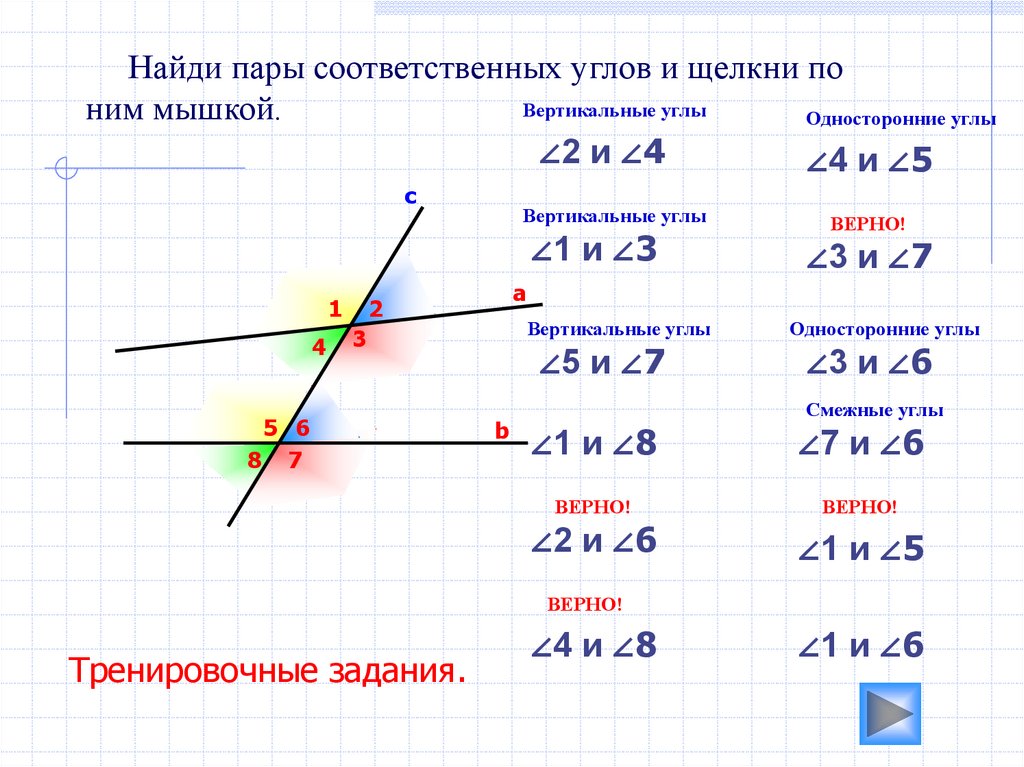
Найди пары соответственных углов и щелкни поВертикальные углы
ним мышкой.
Односторонние углы
∠2 и ∠4
∠4 и ∠5
c
Вертикальные углы
∠1 и ∠3
1
4
∠3 и ∠7
а
2
Вертикальные углы
3
5 6
8 7
ВЕРНО!
∠5 и ∠7
b
Односторонние углы
∠3 и ∠6
Смежные углы
∠1 и ∠8
∠7 и ∠6
ВЕРНО!
ВЕРНО!
∠2 и ∠6
∠1 и ∠5
ВЕРНО!
Тренировочные задания.
∠4 и ∠8
∠1 и ∠6
8.
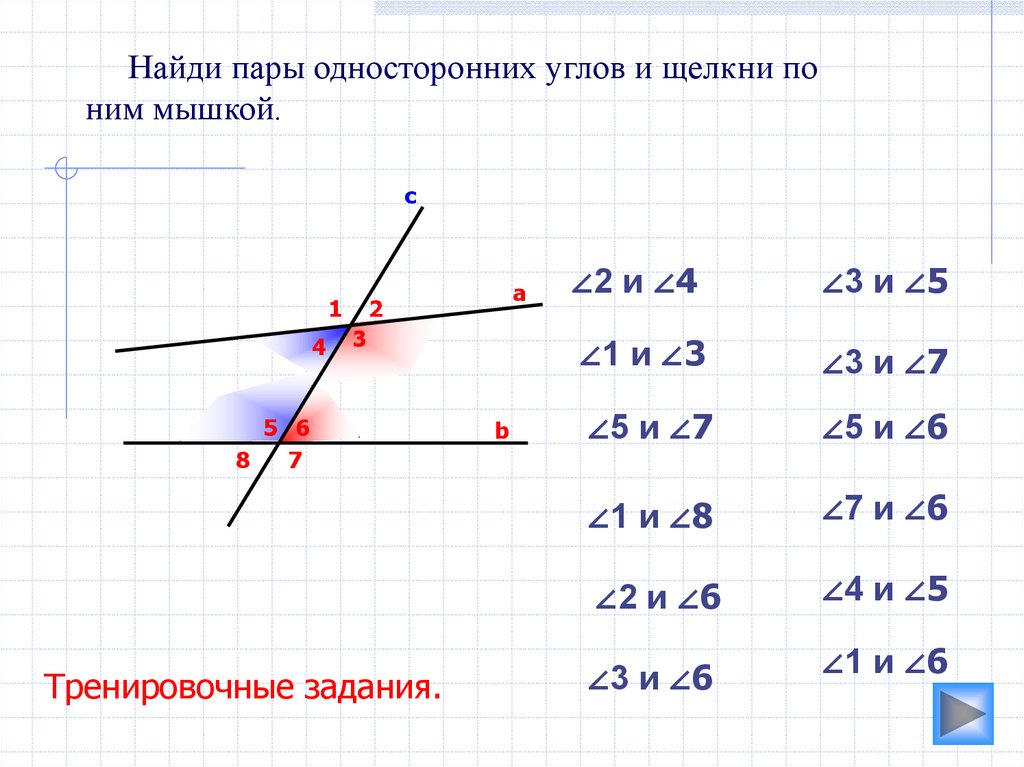
Найди пары односторонних углов и щелкни поним мышкой.
c
1
4
а
2
3
5 6
8
7
Тренировочные задания.
b
∠2 и ∠4
∠3 и ∠5
∠1 и ∠3
∠3 и ∠7
∠5 и ∠7
∠5 и ∠6
∠1 и ∠8
∠7 и ∠6
∠2 и ∠6
∠4 и ∠5
∠3 и ∠6
∠1 и ∠6
9.
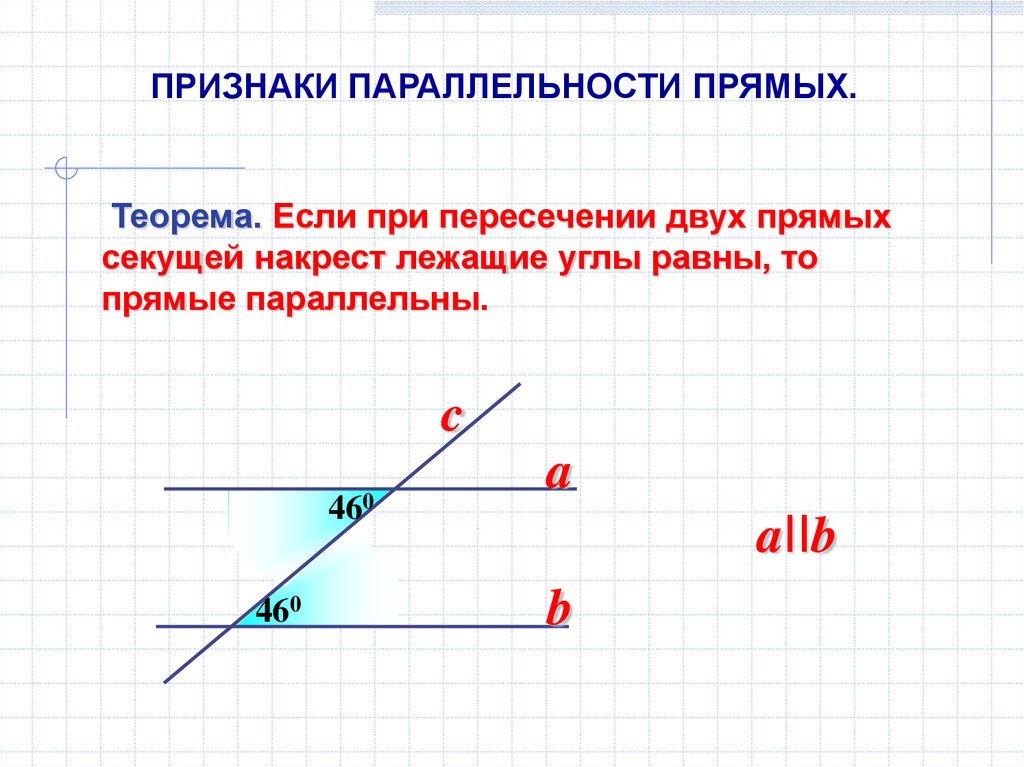
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ.Теорема. Если при пересечении двух прямых
секущей накрест лежащие углы равны, то
прямые параллельны.
c
460
460
a
aIIb
b
10.
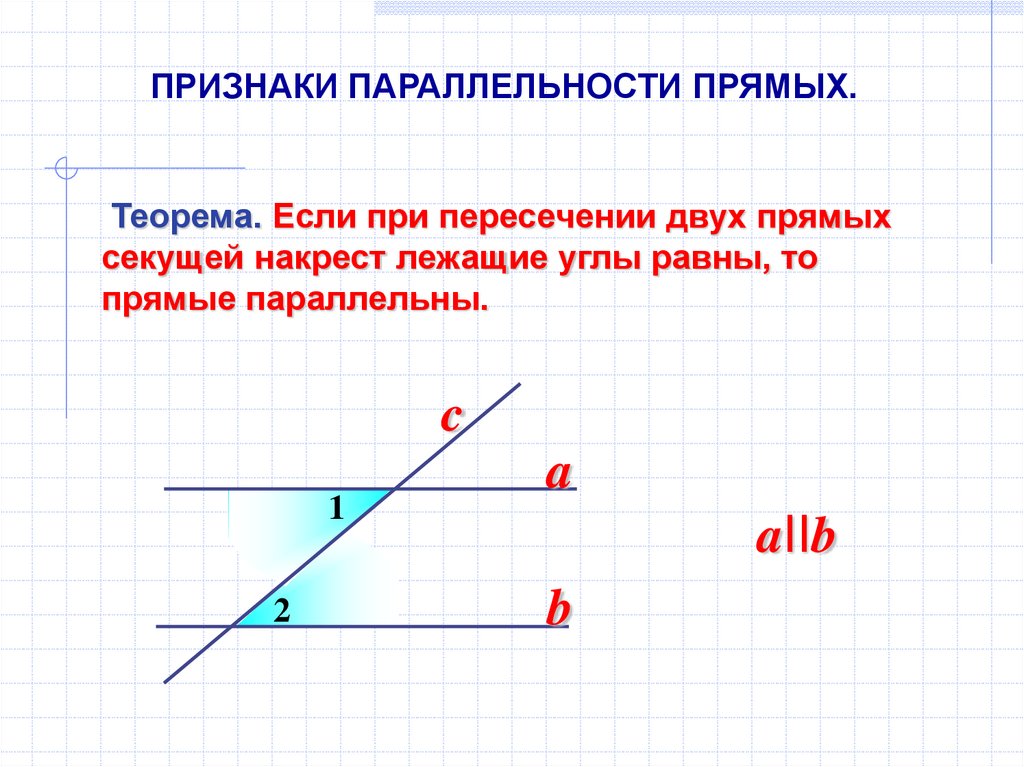
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ.Теорема. Если при пересечении двух прямых
секущей накрест лежащие углы равны, то
прямые параллельны.
c
1
2
a
aIIb
b
11.
Если при пересечении двух прямых секущей накрестУсловие теоремы
лежащие углы равны,
то прямые параллельны.
Заключение теоремы
Дано: НЛУ 1 = 2.
а, b, c- секущая.
c
А
а
В
b
Доказать: aIIb.
Доказательство: 1 случай
Если углы 1 и 2 прямые,
то прямые а и b
перпендикулярны
к прямой АВ, следовательно,
aIIb.
12.
Нc
А
а
О
В
Н1
b
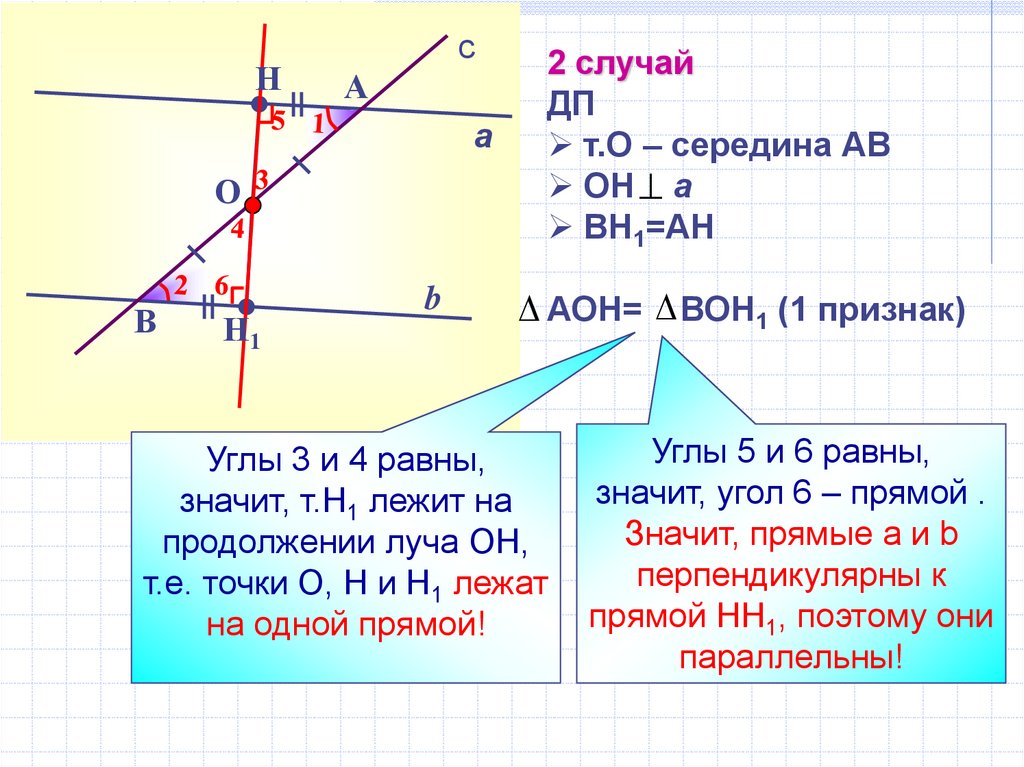
2 случай
ДП
т.О – середина АВ
ОН a
BH1=AH
АОН= ВОН1 (1 признак)
Углы 3 и 4 равны,
значит, т.Н1 лежит на
продолжении луча ОН,
т.е. точки О, Н и Н1 лежат
на одной прямой!
Углы 5 и 6 равны,
значит, угол 6 – прямой .
Значит, прямые a и b
перпендикулярны к
прямой НН1, поэтому они
параллельны!
13.
Если при пересечении двух прямых секущей накрестлежащие углы равны, то прямые параллельны.
Найди на чертежах параллельные прямые a и b и щелкни по ним мышкой.
1
ВЕРНО!!
!
а
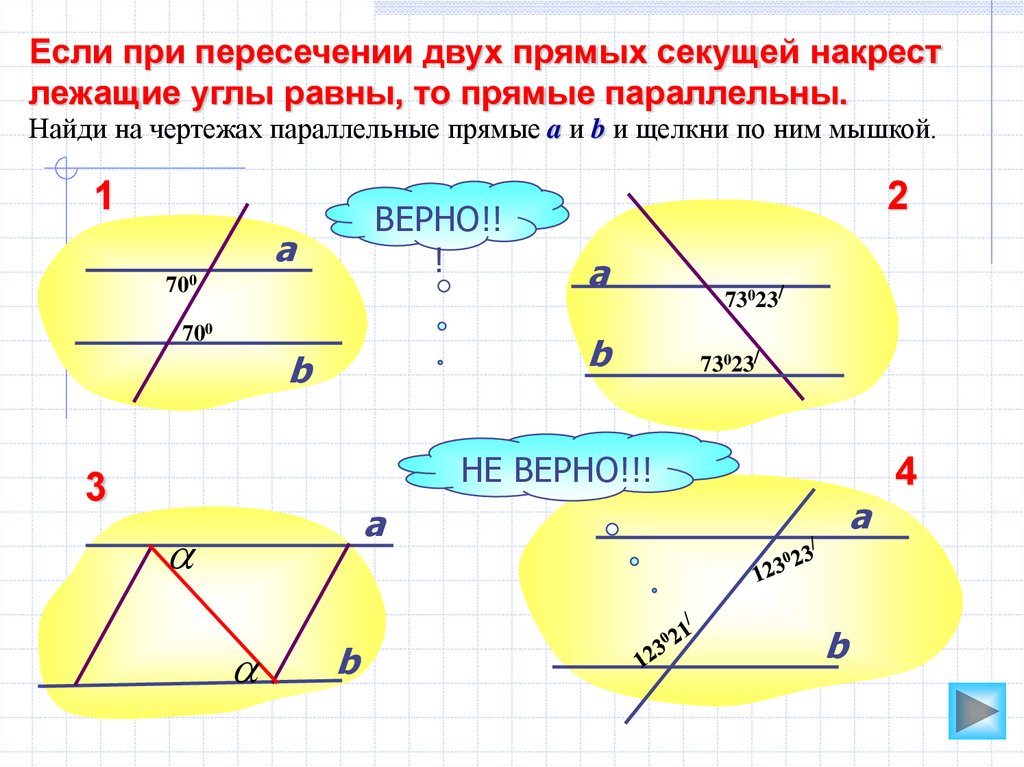
700
700
2
а
b
b
73023/
73023/
НЕ ВЕРНО!!!
3
а
а
b
b
4
14.
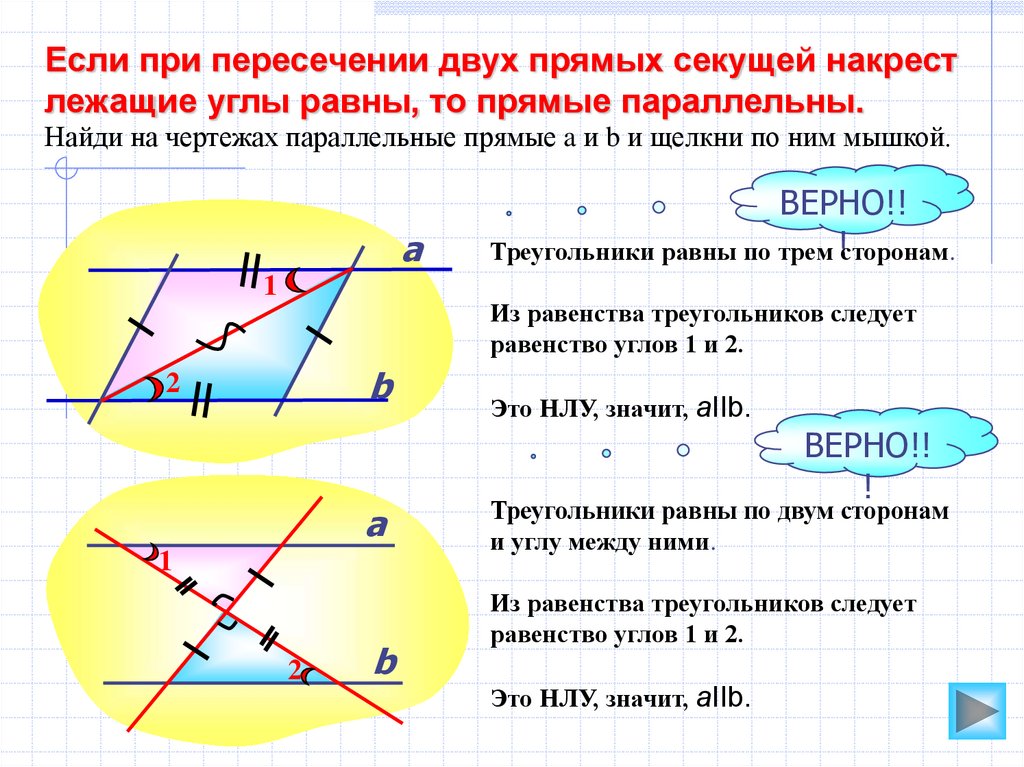
Если при пересечении двух прямых секущей накрестлежащие углы равны, то прямые параллельны.
Найди на чертежах параллельные прямые a и b и щелкни по ним мышкой.
а
1
ВЕРНО!!
Треугольники равны по трем !сторонам.
Из равенства треугольников следует
равенство углов 1 и 2.
b
2
а
1
2
b
Это НЛУ, значит, aIIb.
ВЕРНО!!
!
Треугольники равны по двум сторонам
и углу между ними.
Из равенства треугольников следует
равенство углов 1 и 2.
Это НЛУ, значит, aIIb.
15.
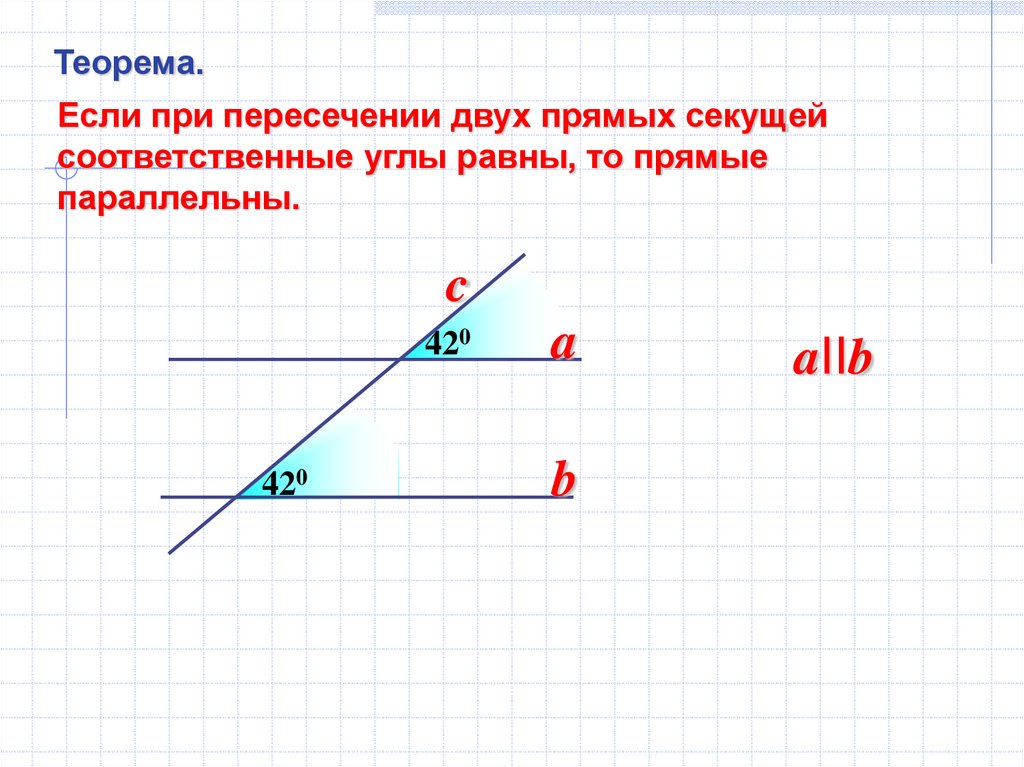
Теорема.Если при пересечении двух прямых секущей
соответственные углы равны, то прямые
параллельны.
c
420
420
a
b
aIIb
16.
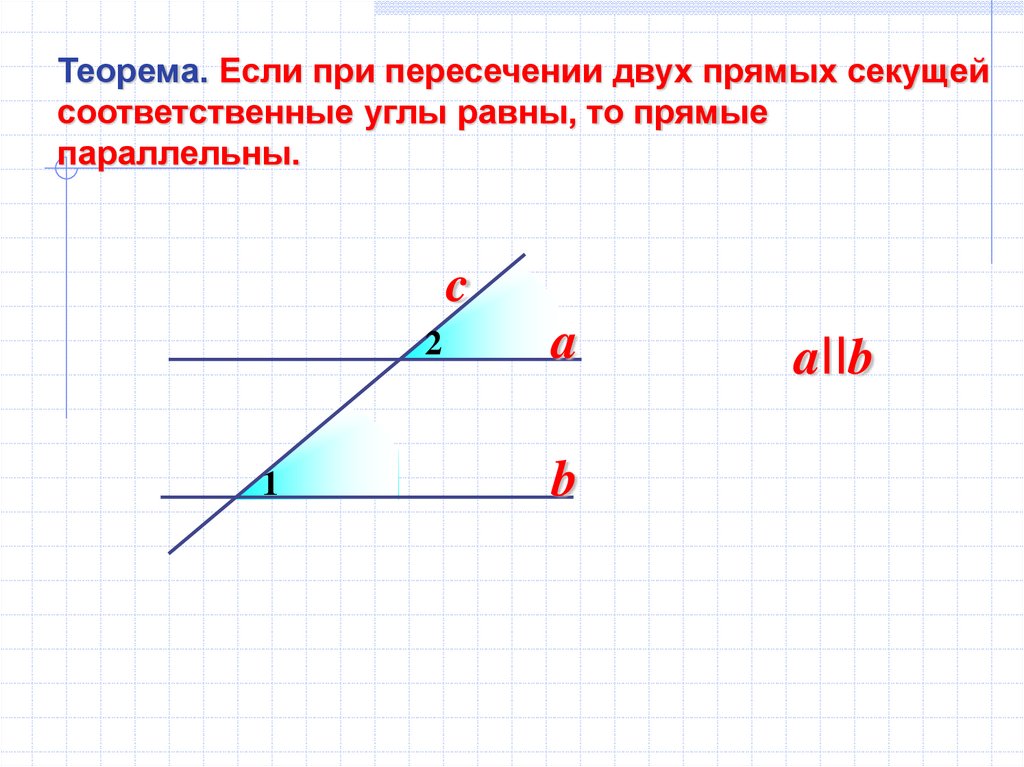
Теорема. Если при пересечении двух прямых секущейсоответственные углы равны, то прямые
параллельны.
c
2
1
a
b
aIIb
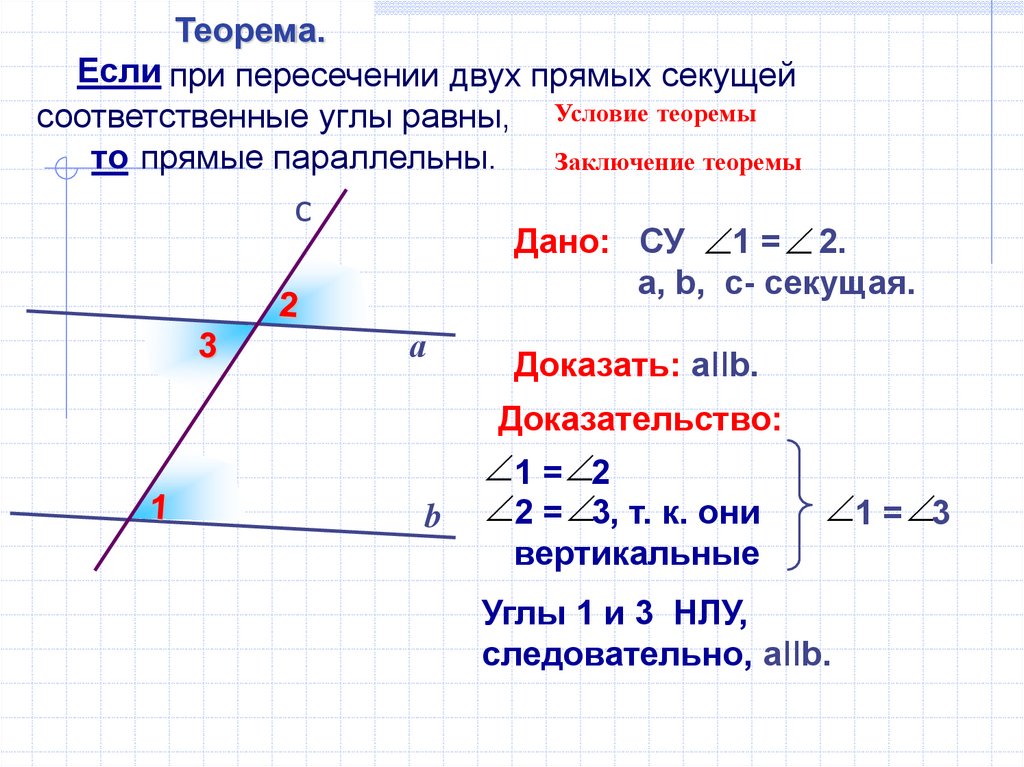
17.
Теорема.Если при пересечении двух прямых секущей
соответственные углы равны, Условие теоремы
то прямые параллельны.
Заключение теоремы
c
Дано: СУ 1 = 2.
а, b, c- секущая.
а
Доказать: aIIb.
Доказательство:
b
1 = 2
2 = 3, т. к. они
1 = 3
вертикальные
Углы 1 и 3 НЛУ,
следовательно, aIIb.
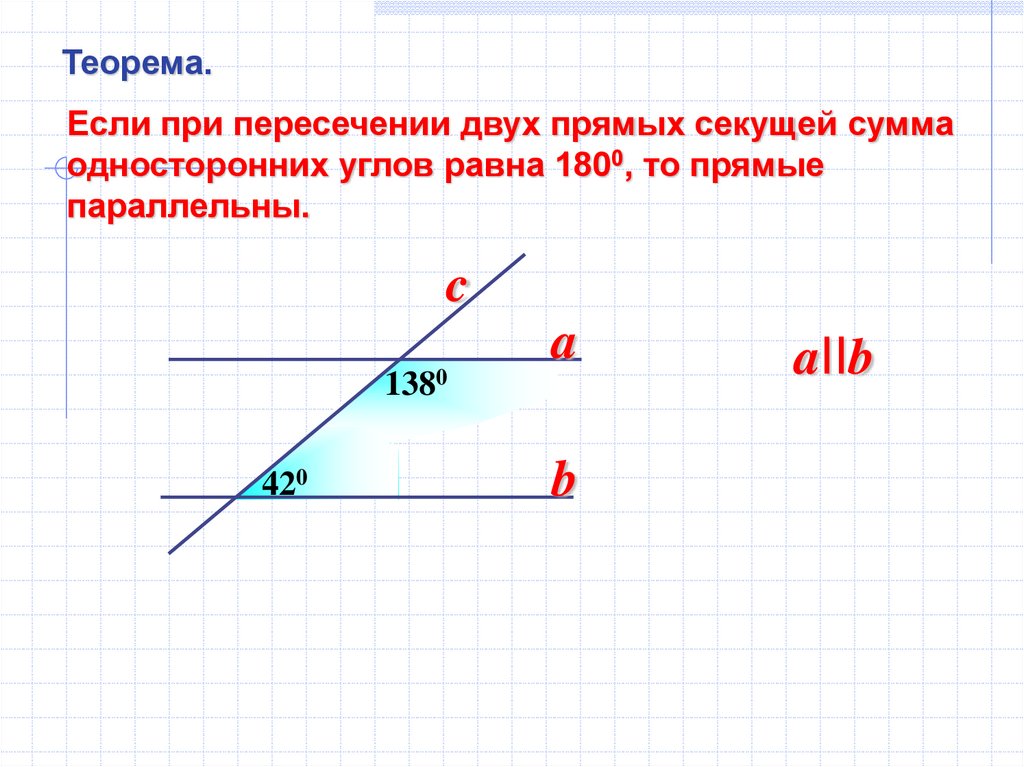
18.
Теорема.Если при пересечении двух прямых секущей сумма
односторонних углов равна 1800, то прямые
параллельны.
c
a
1380
420
b
aIIb
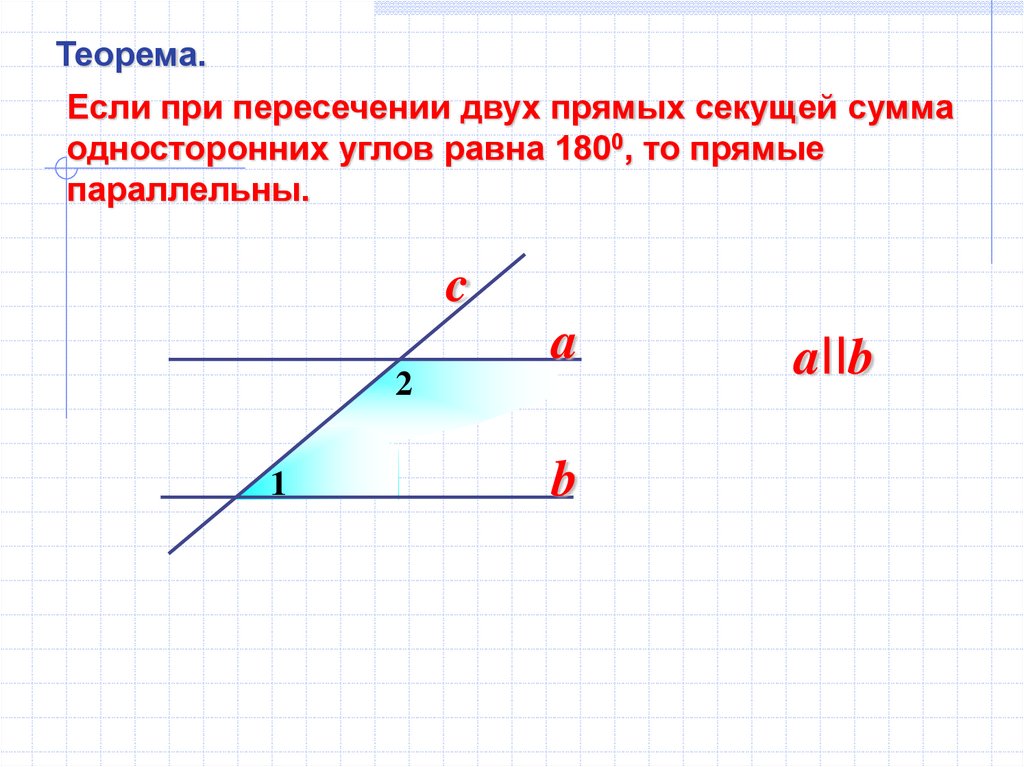
19.
Теорема.Если при пересечении двух прямых секущей сумма
односторонних углов равна 1800, то прямые
параллельны.
c
a
2
1
b
aIIb
20.
Теорема.Если при пересечении двух прямых секущей сумма
односторонних углов равна 1800, Условие теоремы
то прямые параллельны.
Заключение теоремы
c
Дано: ОУ 1 + 2 = 1800.
а, b, c- секущая.
а
Доказать: aIIb.
Доказательство:
b
1 + 2=1800
3 + 2=1800, т.к.
1 = 3
они смежные
Углы 1 и 3 НЛУ,
следовательно, aIIb.





 mathematics
mathematics








