Графическое решение неравенств с двумя переменными

1.

Учитель математики
МОУ лицей №8 г. Ставрополь
Прокофьева И.Л.

2. Этапы урока.

• Организация начала занятия.
• Проверка выполнения домашнего задания.
• Подготовка к усвоению новых знаний.
• Изучение нового материала.
• Первичная проверка знаний.
• Физминутка.
• Закрепление знаний.
• Подведение итогов занятий.
• Домашнее задание.

3. Цели урока:

• Ввести понятие неравенств с двумя
переменными
• Составить алгоритм решения систем
неравенств
• Формировать навыки решения
неравенств и систем неравенств

4. Неравенства с двумя переменными имеют вид:

F(x,y) = y - f(x,y)
F ( x; y ) 0,
F ( x, y ) 0,
F ( x, y ) 0,
F ( x, y ) 0
• Область решения неравенства совокупность всех точек координатной
плоскости, удовлетворяющих заданному
неравенству.

5. Области решения неравенства

F(x,y) ≥ 0
F(x,y)≤0
y
y
0
x
0
x

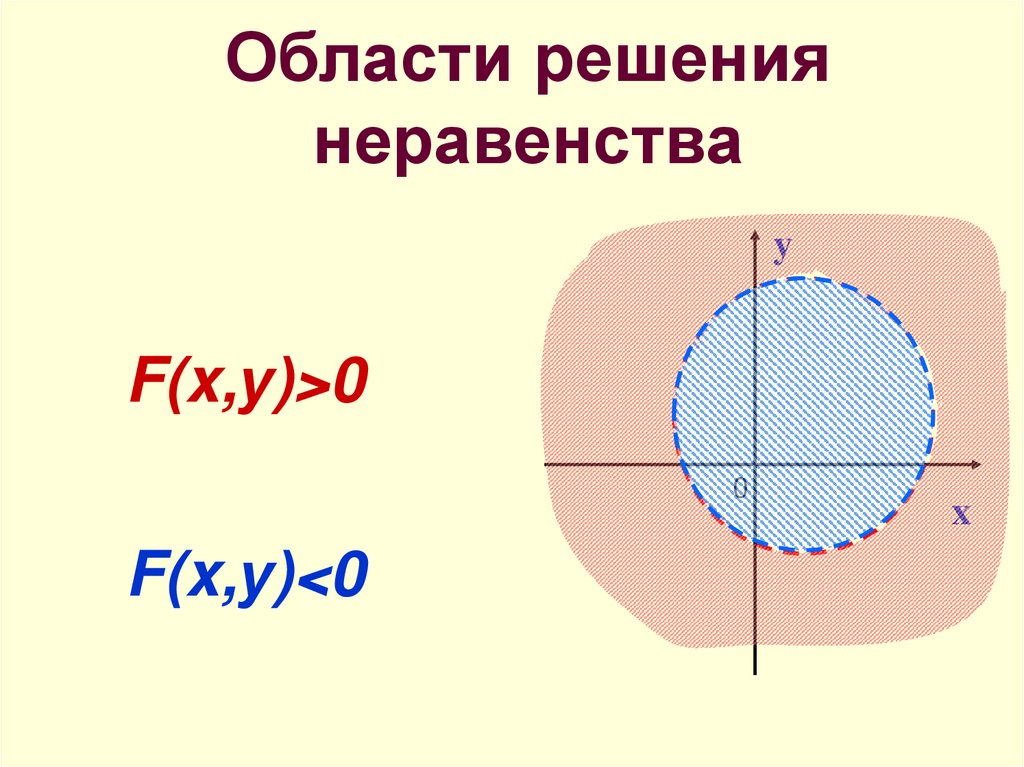
6. Области решения неравенства

y
F(x,у)>0
0
F(x,у)<0
x

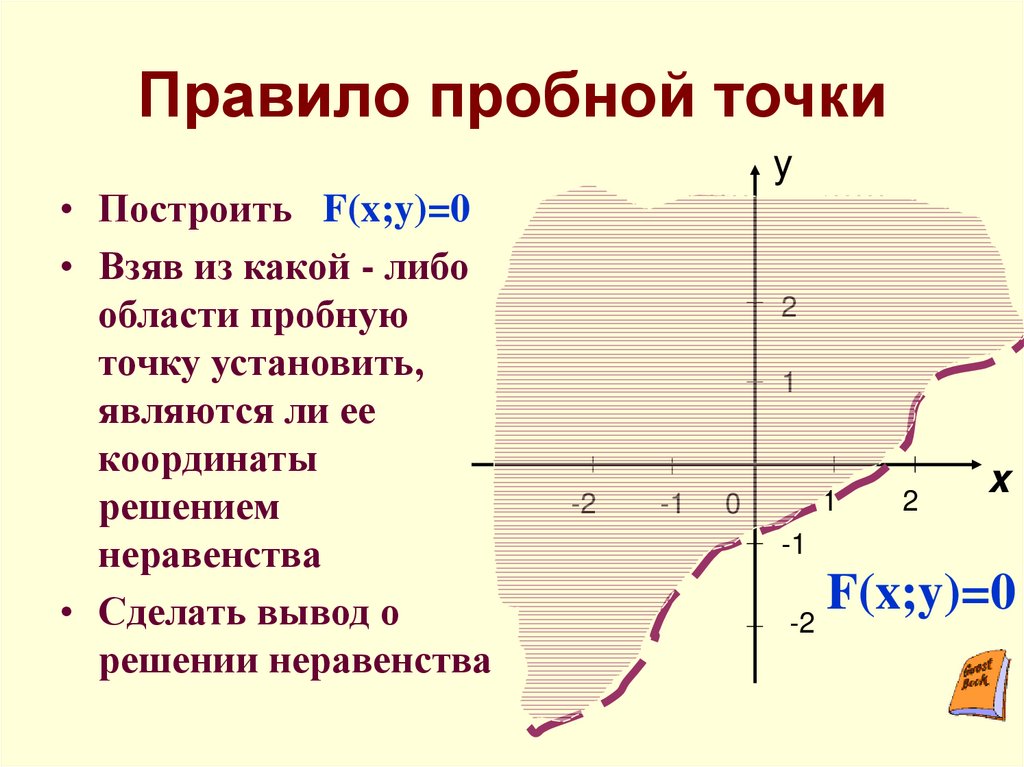
7. Правило пробной точки

y
• Построить F(x;y)=0
• Взяв из какой - либо
области пробную
точку установить,
являются ли ее
координаты
решением
неравенства
• Сделать вывод о
решении неравенства
2
1
-2
-1
1
0
2
x
-1
F(x;y)=0
-2

8.

Решаем вместе

9. Решить неравенство:│х-0,5│-1,5≤0

• Построим график
│х-0,5│-1,5≤0
• Возьмем пробную
точку (3;0),
• найдем значение
│х-0,5│-1,5;
• F(3,0)= 2; 2>0.
y
+
-2
+
2
- +
1
-1
1
0
-1
-2
2
x
- +

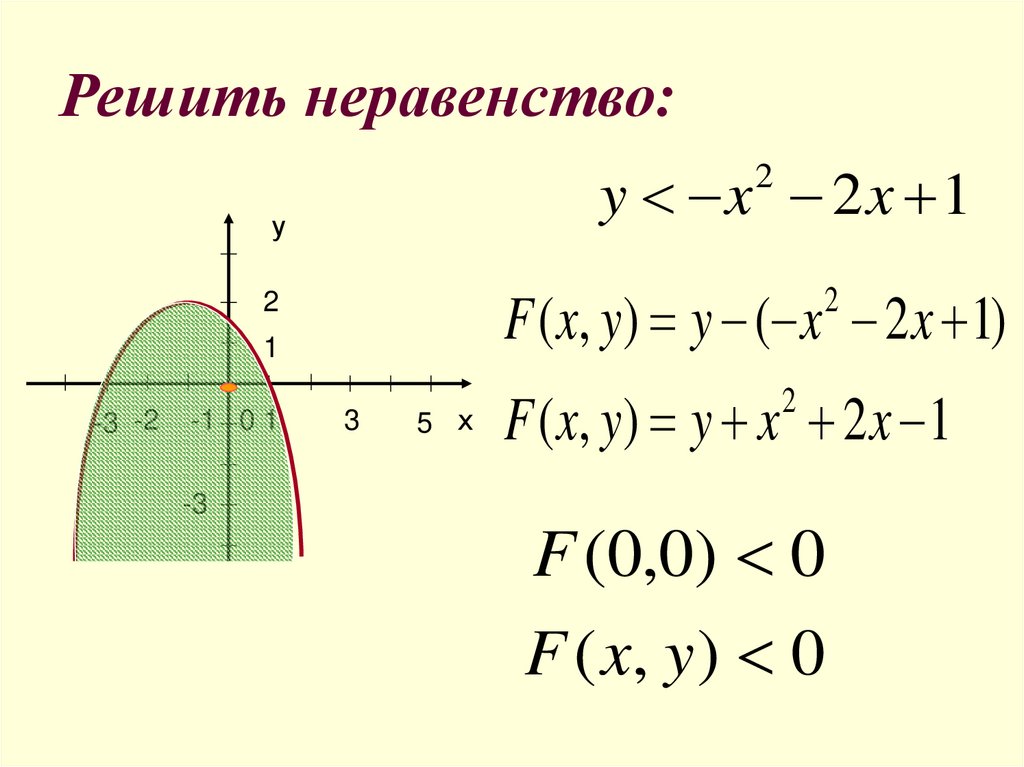
10. Решить неравенство:

y x 2x 1
2
у
F ( x, y) y ( x 2 x 1)
2
2
1
-3 -2
-1 0 1
-3
3
5 х
F ( x, y) y x 2 x 1
2
F (0,0) 0
F ( x, y ) 0

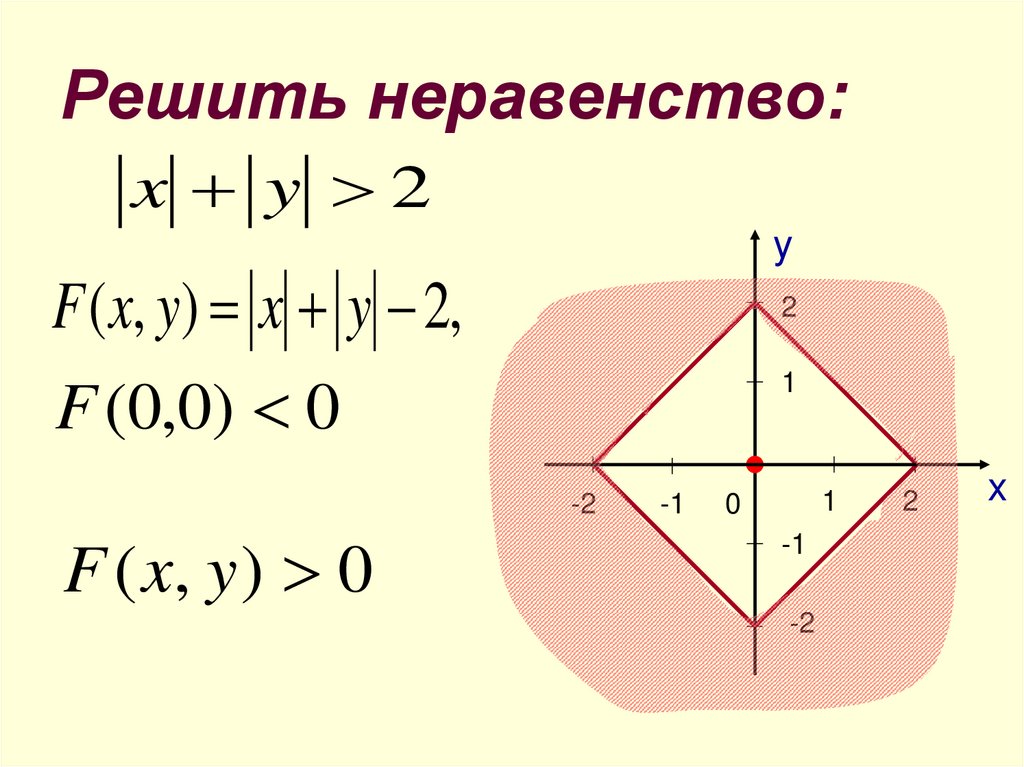
11. Решить неравенство:

x y 2
y
F ( x, y) x y 2,
F (0,0) 0
2
1
-2
F ( x, y ) 0
-1
1
0
-1
-2
2
x

12.

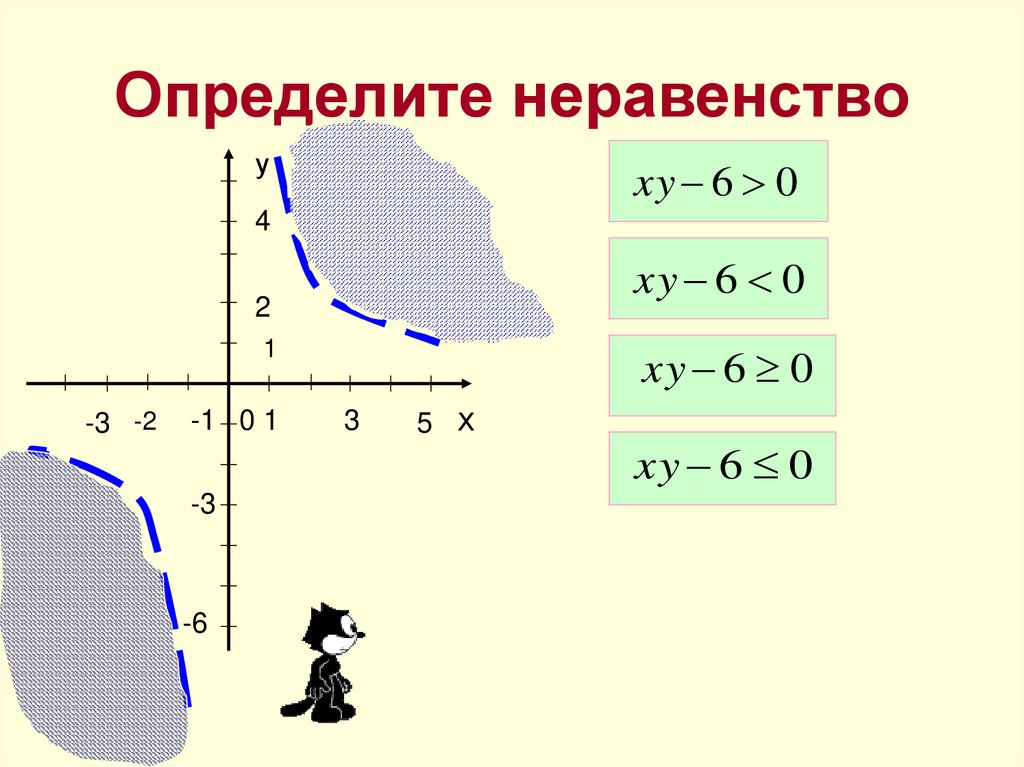
Тестирование

13. Определите неравенство

у
xy 6
8
00
4
xy 6 0
2
1
-3 -2
-1 0 1
-3
-6
xy 6 0
3
5 х
xy 6 0

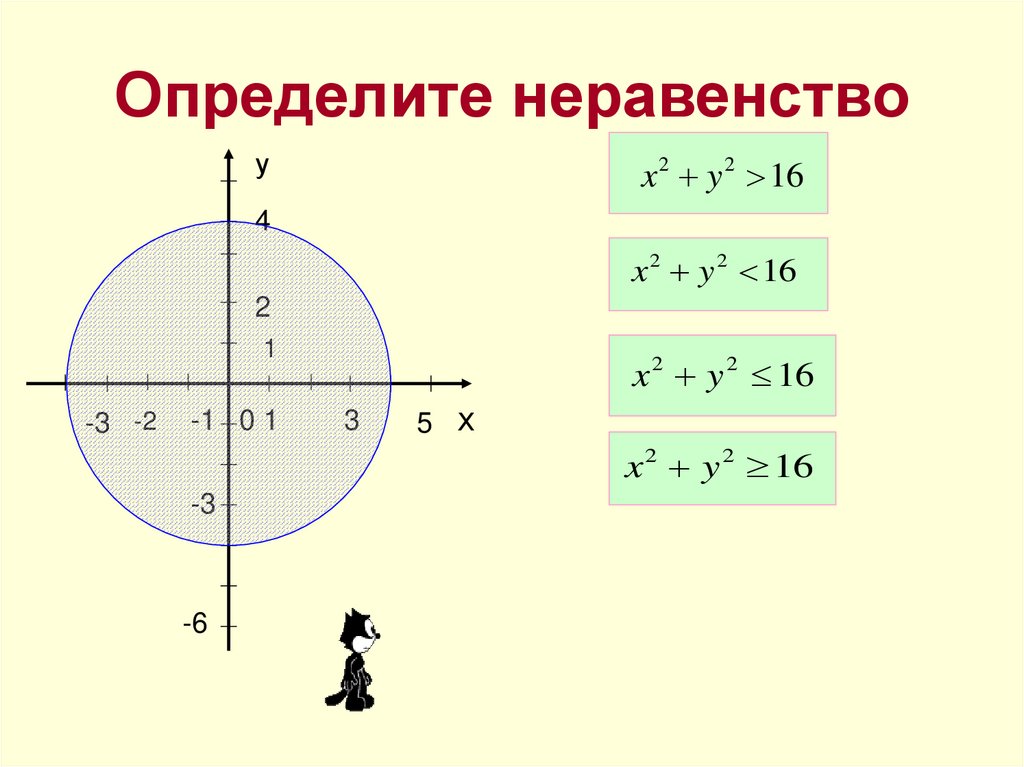
14. Определите неравенство

у
x 2 y 2 16
4
x 2 y 2 16
xy 8 0
2
1
-3 -2
-1 0 1
x 2 y 2 16
3
5 х
x 2 y 2 16
-3
-6

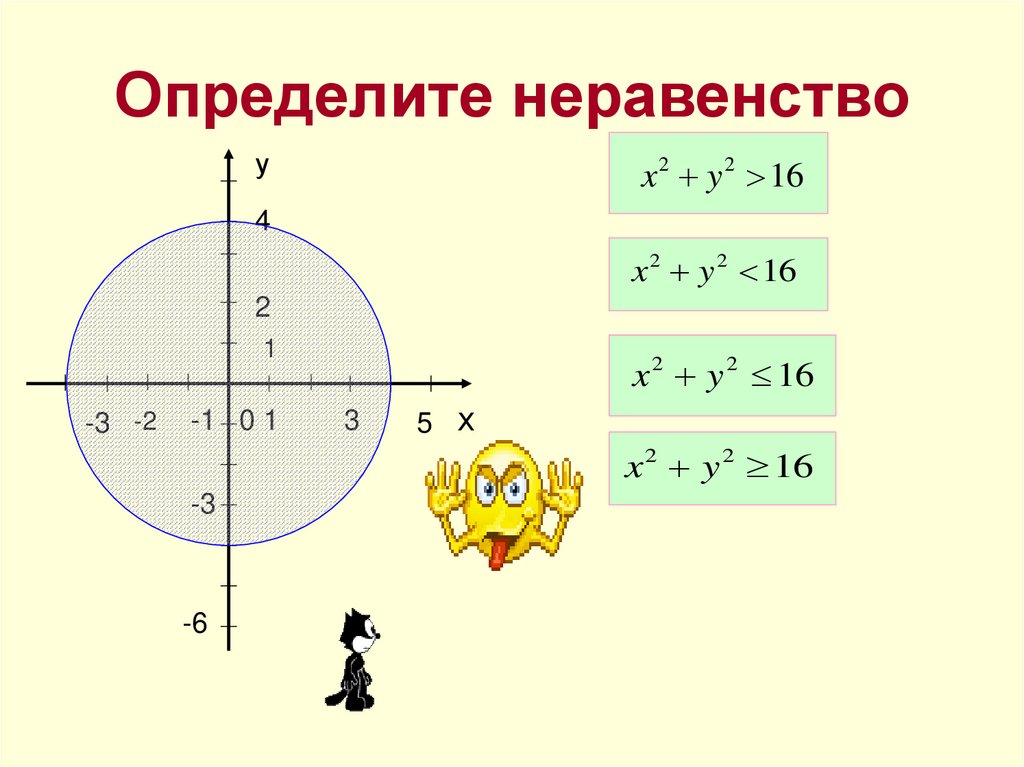
15. Определите неравенство

у
x 2 y 2 16
4
x 2 y 2 16
xy 8 0
2
1
-3 -2
-1 0 1
x 2 y 2 16
3
5 х
x 2 y 2 16
-3
-6

16. Определите неравенство

у
xy 6 0
4
xy 6 0
2
1
-3 -2
-1 0 1
-3
-6
xy 6 0
3
5 х
xy 6 0

17. Определите неравенство

у
x 2 y 2 16
4
x 2 y 2 16
xy 8 0
2
1
-3 -2
-1 0 1
x 2 y 2 16
3
5 х
x 2 y 2 16
-3
-6

18. Правило пробной точки при решении систем неравенств.

• Построить
• F(x;y)=0 и G(x;y)=0
• Взяв из каждой области
пробную точку
установить, являются ли
ее координаты решением
системы
• Объединение полученных
областей- решение
системы неравенств
y
2
1
-2
-1
1
0
-1
-2
2
x

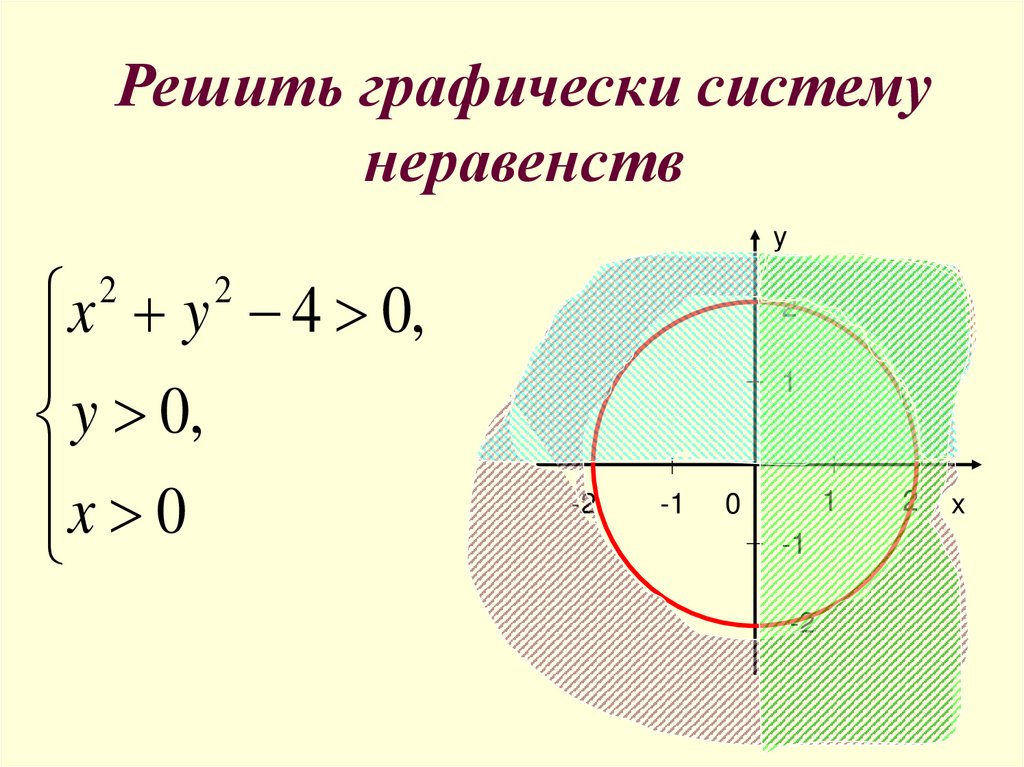
19. Решить графически систему неравенств

y
x y 4 0,
y 0,
x 0
2
2
2
1
-2
-1
1
0
-1
-2
2
x

20. Решить графически неравенство:

( y x)( x y 1)( x 2) 0
• Строим сплошными
линиями графики:
y
y x
2
y x 1
x 2
1
-2
-1
1
0
-1
-2
2
x

21. Определим знак неравенства в каждой из областей

F ( x, y ) ( y x)( x y 1)( x 2)
F (3,0) 0,
F (0,3) 0,
F ( 3,4) 0,
F ( 3,0) 0,
F ( 3, 4) 0,
F (0, 2) 0,
F ( 1,0) 0
3
+
2
2
-
y
1
4
-
1
-2
-1
1
0
+ 7
-1
-2
5
6
-
2
x
+

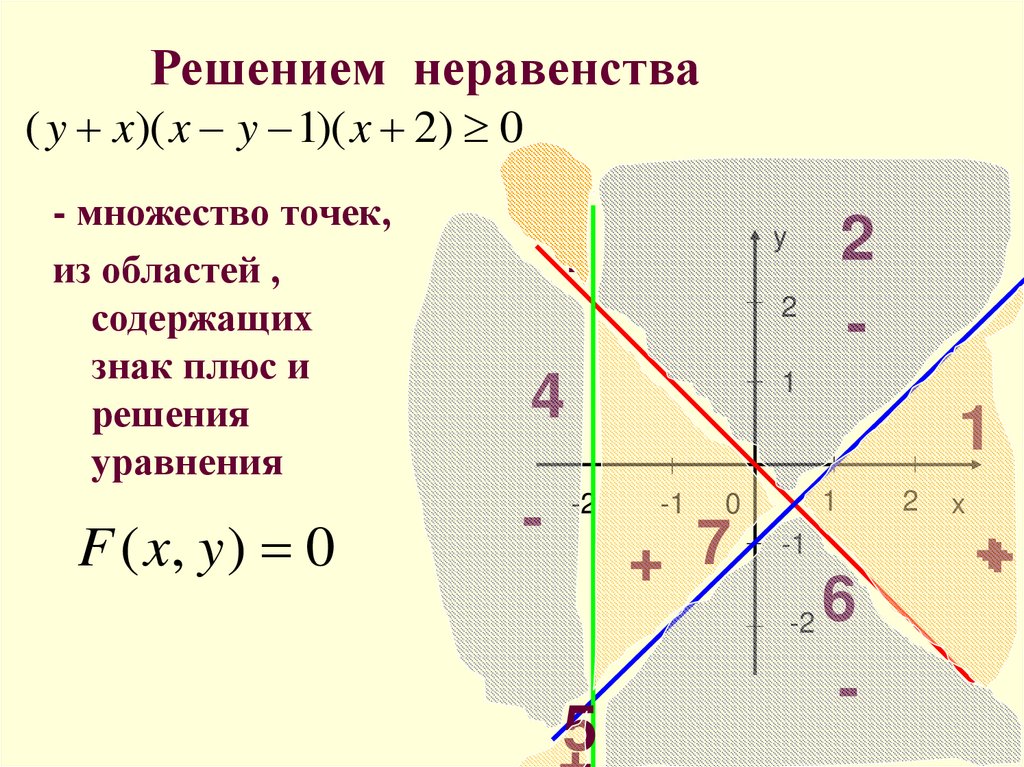
22. Решением неравенства

( y x)( x y 1)( x 2) 0
- множество точек,
из областей ,
содержащих
знак плюс и
решения
уравнения
F ( x, y ) 0
3
+
2
2
-
y
1
4
-
1
-2
-1
1
0
+ 7
-1
-2
5
6
-
2
x
+

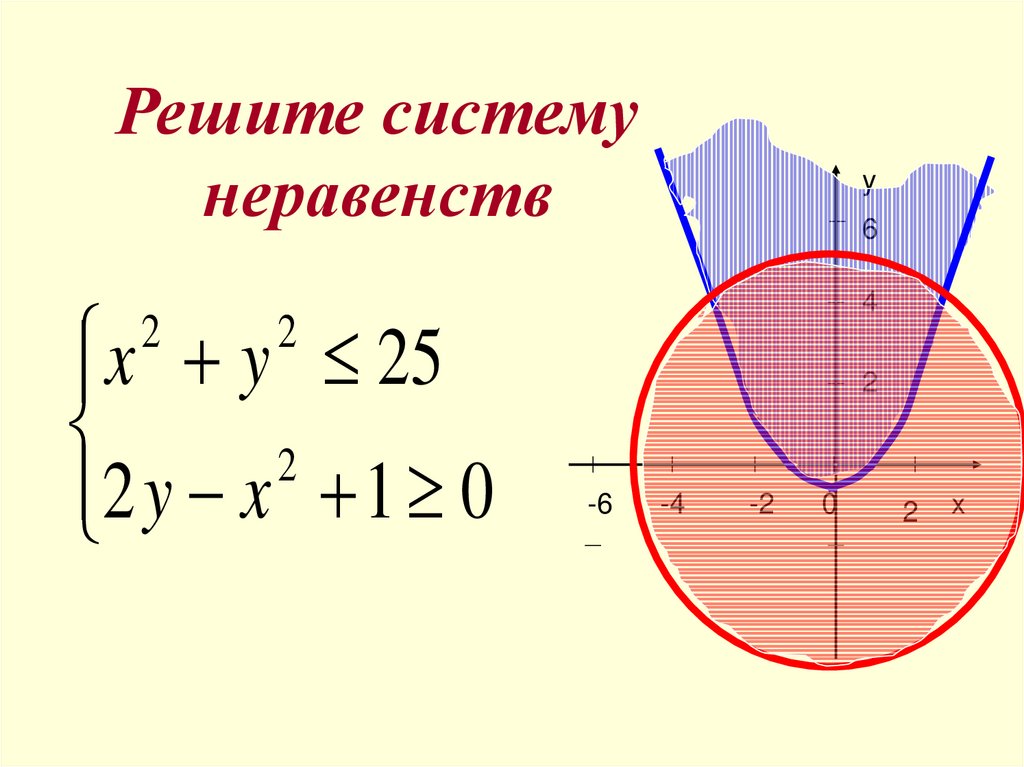
23. Решите систему неравенств

x y 25
2
2 y x 1 0
2
y
6
4
2
2
-6
-4
-2
0
2
x

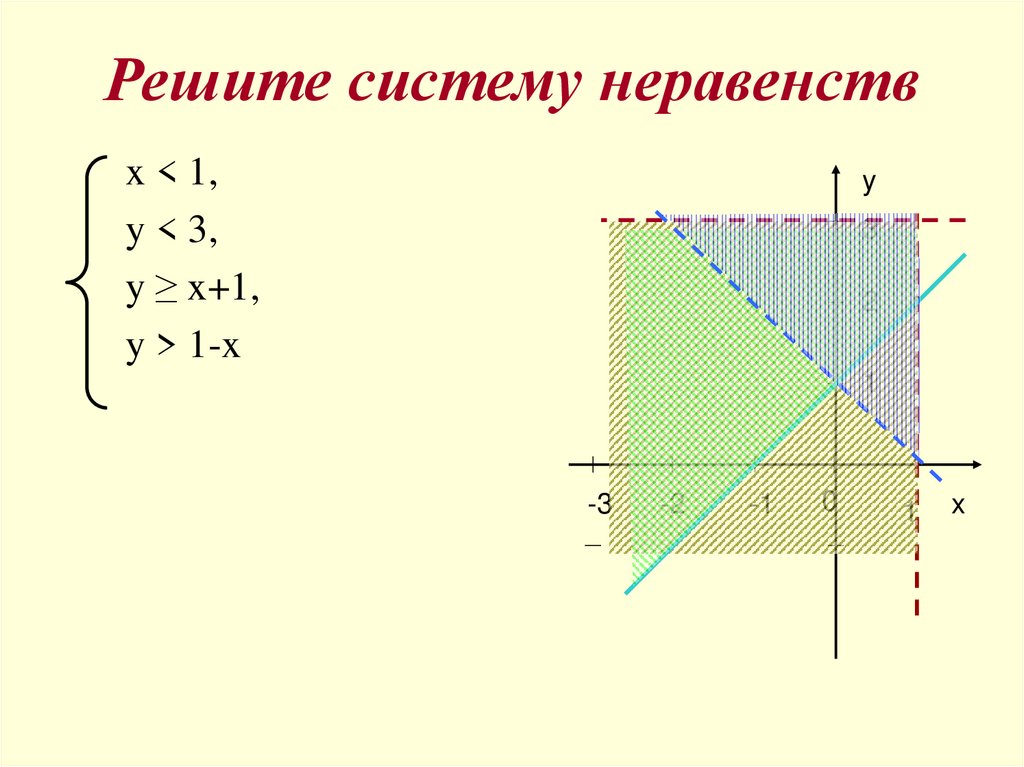
24. Решите систему неравенств

x < 1,
y < 3,
y ≥ x+1,
y > 1-x
y
3
2
1
-3
-2
-1
0
1
x

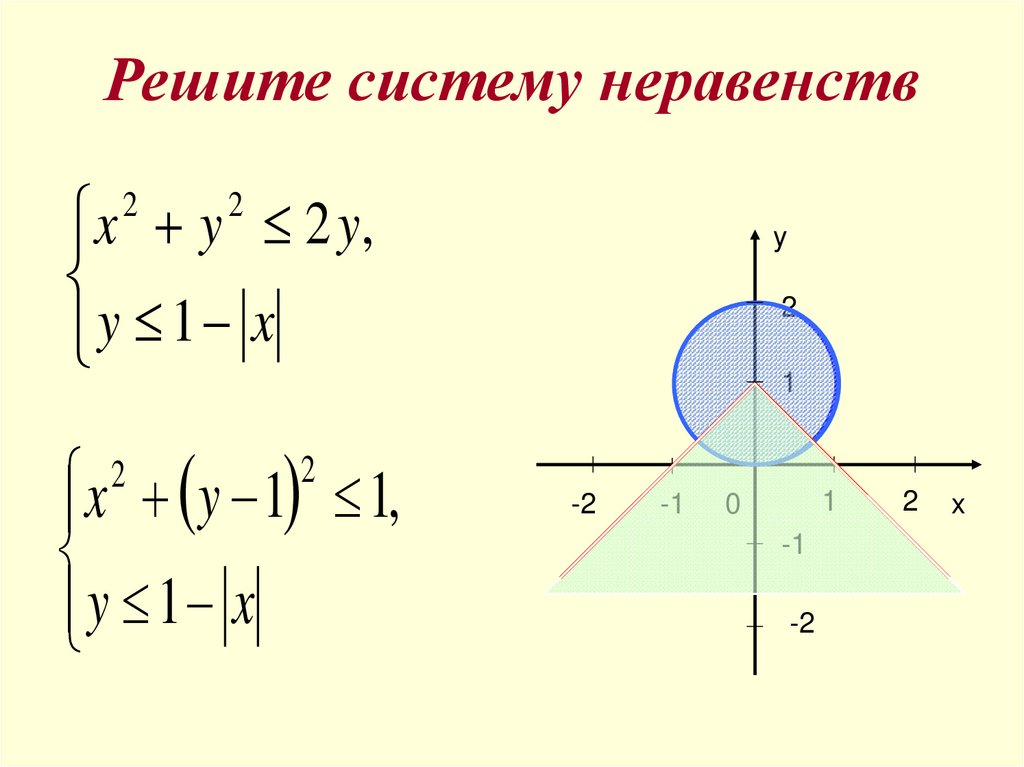
25. Решите систему неравенств

x y 2 y,
y 1 x
2
2
x y 1 1,
y 1 x
2
y
2
1
2
-2
-1
1
0
-1
-2
2
x

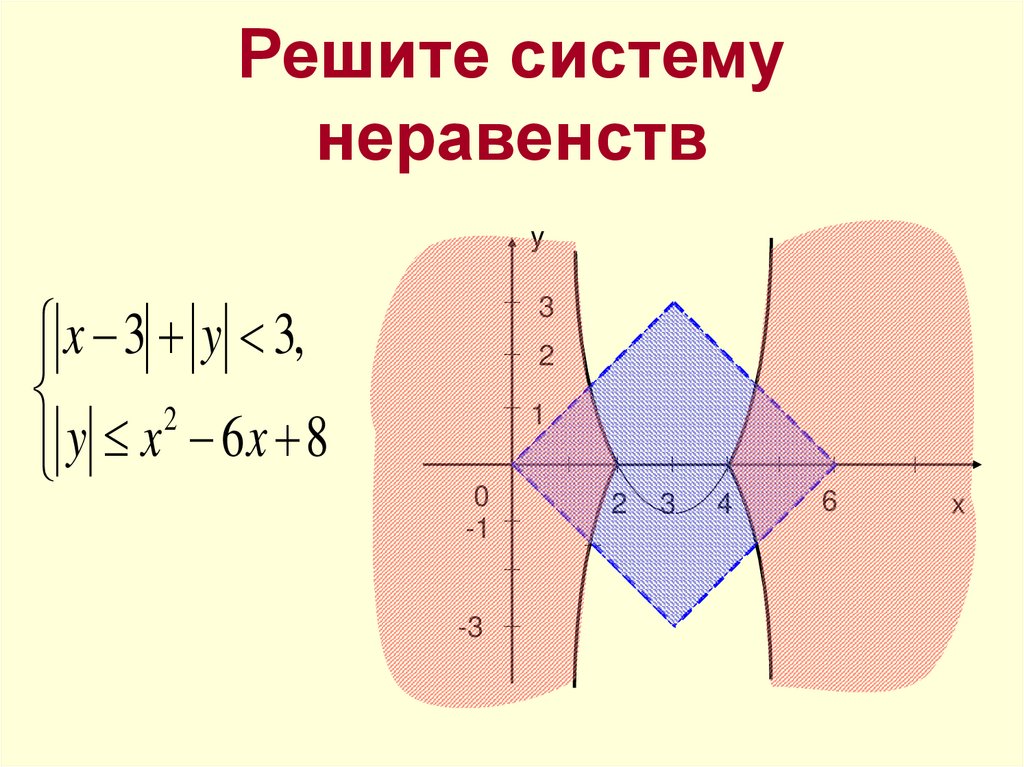
26. Решите систему неравенств

y
x 3 y 3,
2
y x 6 x 8
3
2
1
0
-1
-3
2
3
4
6
x