Similar presentations:
Теоретические основы химии
1.
Теоретические основыхимии
Разделы курса:
1.
Строение вещества, строение молекул. Природа
химической связи.
2.
Химическая термодинамика.
3.
Учение о растворах. Растворы электролитов.
(В курсе будут лишь упомянуты строение вещества в
кристаллическом состоянии, химическая кинетика и
целый ряд других вопросов).
2.
Учебники и учебные пособия1.
2.
3.
Основная литература:
Карапетьянц М.Х., Дракин С.И. Общая и неорганическая химия.
М.: Химия. 1992 2004. 592 с.
Общая и неорганическая химия. В 2 т. / под ред. А.Ф. Воробьева.
Том 1. Теоретические основы химии. М.: ИКЦ «Академкнига».
2004. 371 с.
Практикум по неорганической химии. Под ред. А.Ф. Воробьева
и С.И. Дракина. М.: Химия. 1983. 246 с.
Дополнительная литература:
1.
Неорганическая химия. В 3 т. / под ред. Ю.Д. Третьякова. Том 1
3.
Строение веществаЗаконы микромира отличны от законов макромира.
Атом наименьшая частица химического элемента, являющаяся
носителем его свойств.
Атомы существуют в реальности и могут быть визуализированы.
Просвечивающая
электронная
микроскопия
Сканирующая зондовая
микроскопия (сканирующая
туннельная микроскопия и атомносиловая микроскопия)
4.
Экспериментальная основа наших знаний об энергетическомсостоянии электронов в атомах получение и интерпретация
атомных спектров.
Атомные спектры, спектры оптические получаются при испускании
или поглощении света (электромагнитных волн) свободными или
слабо связанными атомами; такими спектрами обладают, в
частности, одноатомные газы и пары. Атомные спектры
линейчатые (состоят из достаточно узких линий в отличие от
молекул, у которых спектры полосатые).
Наиболее простым является спектр атома водорода (нет
межэлектронных взаимодействий).
R = 109 677 см−1
Постоянная Ридберга
5.
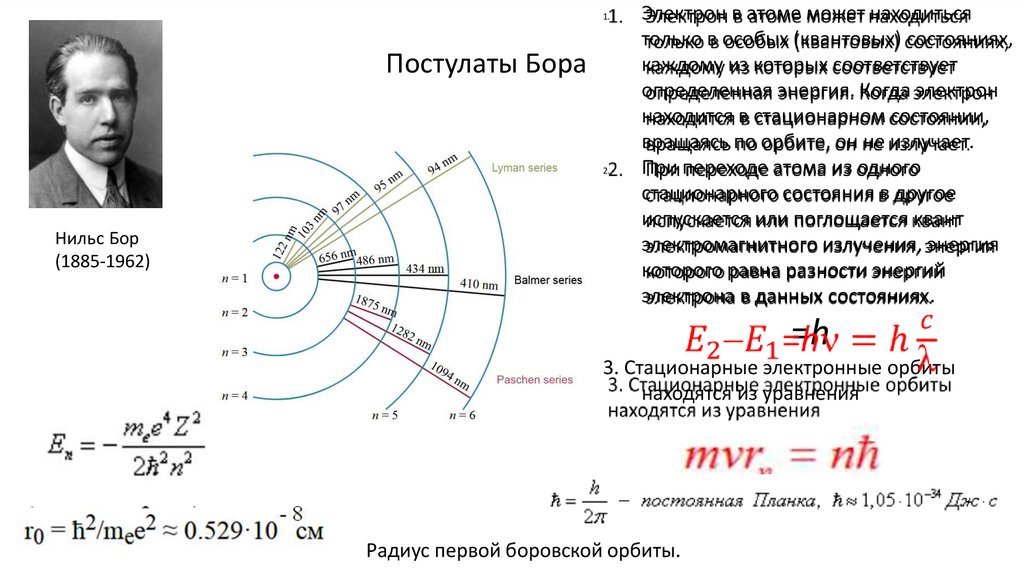
1.Постулаты Бора
2.
Нильс Бор
(1885-1962)
Электрон в атоме может находиться
только в особых (квантовых) состояниях,
каждому из которых соответствует
определенная энергия. Когда электрон
находится в стационарном состоянии,
вращаясь по орбите, он не излучает.
При переходе атома из одного
стационарного состояния в другое
испускается или поглощается квант
электромагнитного излучения, энергия
которого равна разности энергий
электрона в данных состояниях.
=h
3. Стационарные электронные орбиты
находятся из уравнения
Радиус первой боровской орбиты.
6.
Волновые свойства материальных объектовТеория Бора встретила трудности при описании спектров
многоэлектронных атомов.
Нужно учитывать свойства микрообъектов. Законы движения
микрочастиц отличны от законов движения макрочастиц.
В начале XX века стало ясно, что микрочастицы (все) обладают
волновыми свойствами.
Фотон обладает свойствами и частицы (давление света, эффект
Комптона – увеличение длины волны рассеянного излучения по
сравнению с длиной волны падающего излучения), и волны (метод
рентгеновской дифракции – основной метод исследования структуры
кристаллических тел).
Дифракция электронов (электронография).
7.
Соотношение де Бройля (в нерелятивистском пределе)Для электрона, ускоряющегося в электрическом поле с разностью
потенциалов :
В ультрарелятивистком пределе:
8.
Соотношение неопределенностейГейзенберга
Невозможно одновременно точно определить
координату и импульс квантовой частицы
В.К. Гейзенберг
(1901-1976)
x – среднеквадратичное отклонение координаты
p – среднеквадратичное отклонение импульса.
Равенство достигается тогда и только E
тогда,
когда форма в изменении
– неопределенность
представления вектора состояния системы
в координатном
энергии квантовой
системы в процессе,
представлении совпадает с формой его представления
длящемсяв t.
импульсном представлении (не меняется при преобразовании
9.
Волновая функцияВолновая функция (пси-функция) – комплекснозначная функция,
используемая в квантовой механике для описания чистого
состояния системы.
Плотность вероятности нахождения частицы в данной точке
конфигурационного пространства в данный момент времени
считается равной квадрату абсолютного значения волновой
функции этого состояния в координатном представлении.
По всему
Вероятность нахождения частицы в данном объеме пространства:
пространству
10.
Уравнение ШрёдингераОписывает состояние электрона в атоме.
В трехмерном пространстве, форма, зависящая от времени:
Э. Шрёдингер
(1887-1961)
Стационарное уравнение Шрёдингера:
11.
Решение уравнения Шрёдингера. Квантовыечисла
Для атомов уравнение решается в сферических координатах:
Решение записывается в виде произведения радиальной и
волновой функций:
12.
Полная энергия электрона квантована:13.
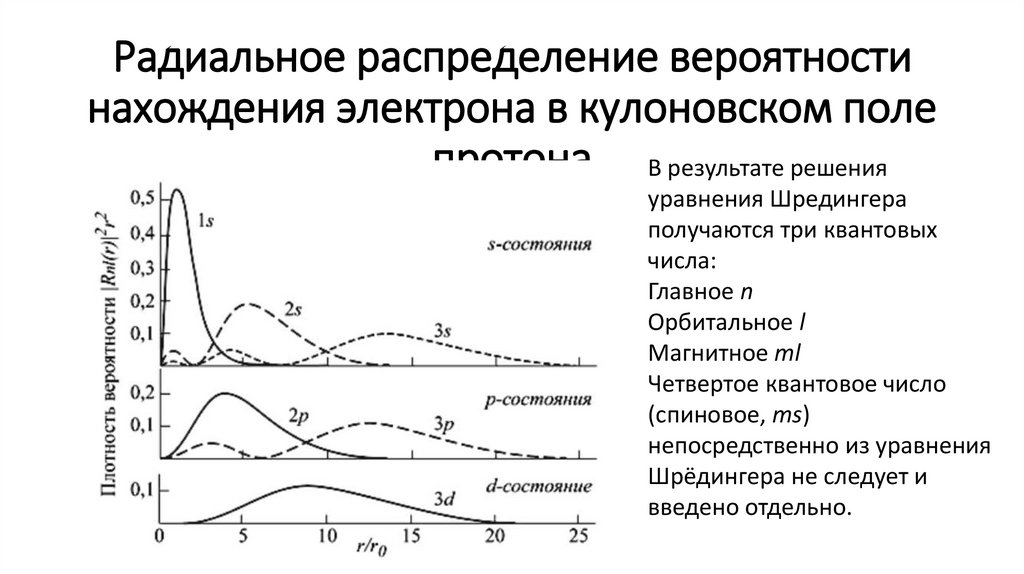
Радиальное распределение вероятностинахождения электрона в кулоновском поле
протона В результате решения
уравнения Шредингера
получаются три квантовых
числа:
Главное n
Орбитальное l
Магнитное ml
Четвертое квантовое число
(спиновое, ms)
непосредственно из уравнения
Шрёдингера не следует и
введено отдельно.
14.
Главное квантовое число nХарактеризует общую энергию электрона.
В одноэлектронной системе энергия электрона зависит только от n.
В многоэлектронных атомах энергия дополнительно зависит от l.
n принимает значения натуральных чисел 1, 2, 3, ….
Характеризует «удаленность» электрона от ядра.
15.
Орбитальное квантовое число lЭлектронная орбиталь – это область пространства, в которой
нахождение электрона наиболее вероятно (более 95 %).
Форма электронной орбитали характеризуется орбитальным
квантовым числом l. l изменяется от 0 до (n 1), принимая
целочисленные значения.
Обозначения атомных орбиталей.
Возможны:
1s
2s 2p
3s 3p 3d
4s 4p 4d 4f
5s 5p 5d 5f 5g
16.
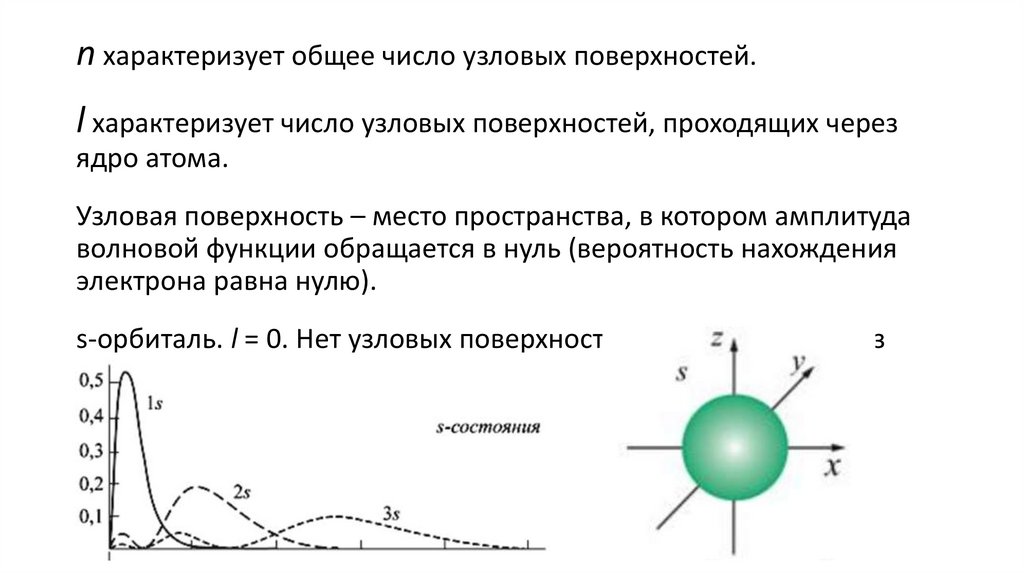
n характеризует общее число узловых поверхностей.l характеризует число узловых поверхностей, проходящих через
ядро атома.
Узловая поверхность – место пространства, в котором амплитуда
волновой функции обращается в нуль (вероятность нахождения
электрона равна нулю).
s-орбиталь. l = 0. Нет узловых поверхностей, проходящих через
ядро. Имеет сферическую форму.
17.
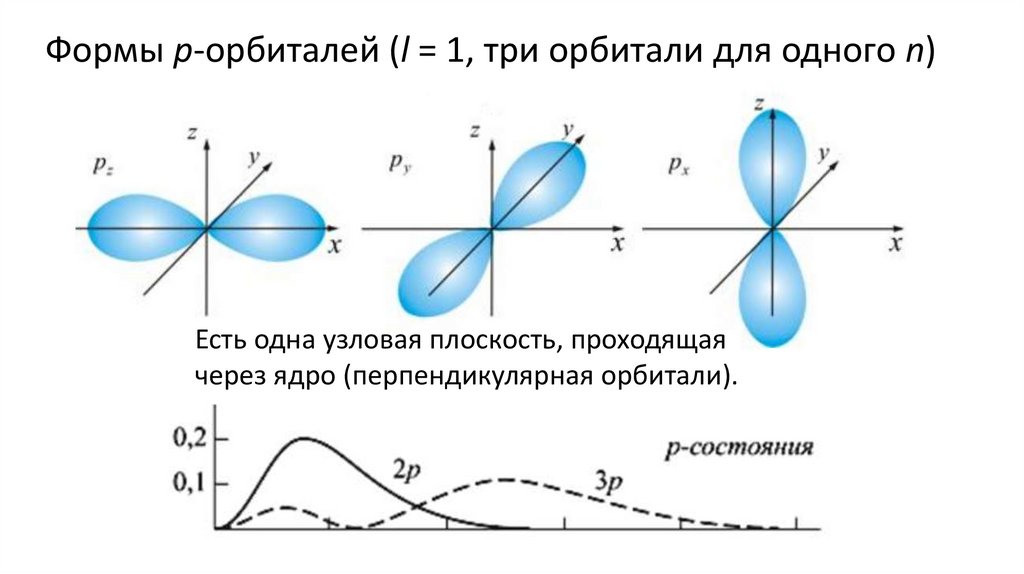
Формы p-орбиталей (l = 1, три орбитали для одного n)Есть одна узловая плоскость, проходящая
через ядро (перпендикулярная орбитали).
18.
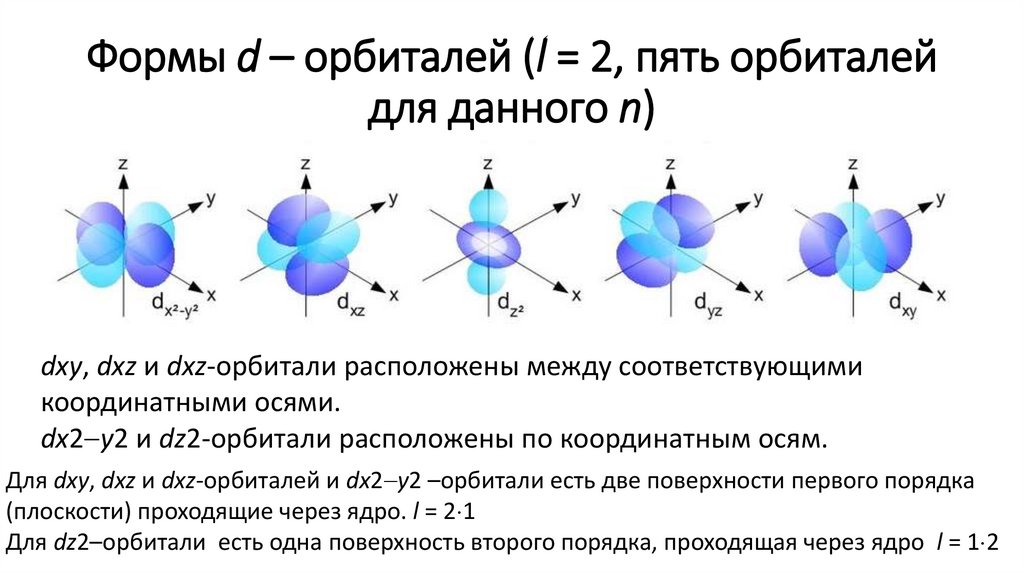
Формы d – орбиталей (l = 2, пять орбиталейдля данного n)
dxy, dxz и dxz-орбитали расположены между соответствующими
координатными осями.
dx2 y2 и dz2-орбитали расположены по координатным осям.
Для dxy, dxz и dxz-орбиталей и dx2 y2 –орбитали есть две поверхности первого порядка
(плоскости) проходящие через ядро. l = 2 1
Для dz2–орбитали есть одна поверхность второго порядка, проходящая через ядро l = 1 2
19.
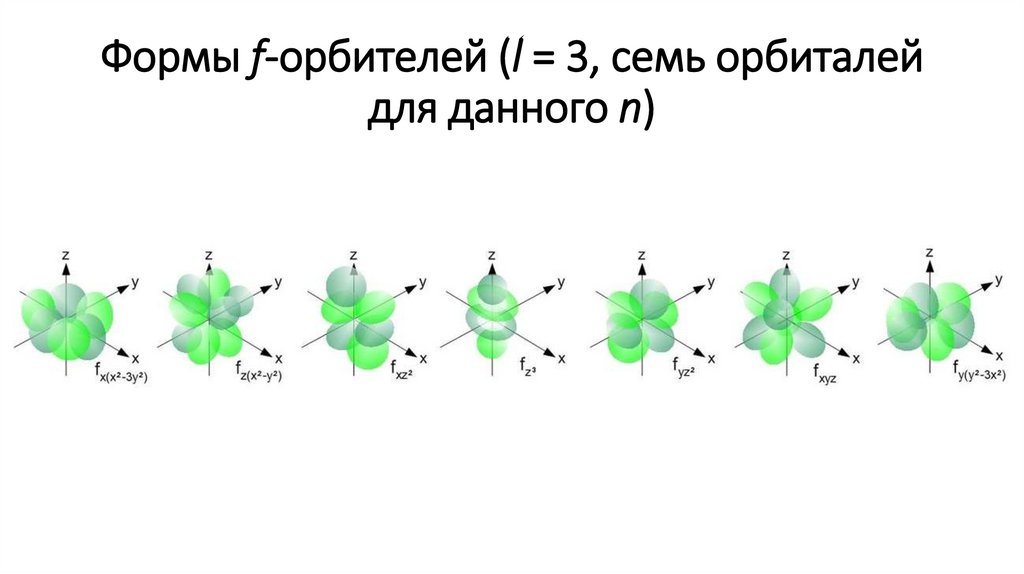
Формы f-орбителей (l = 3, семь орбиталейдля данного n)
20.
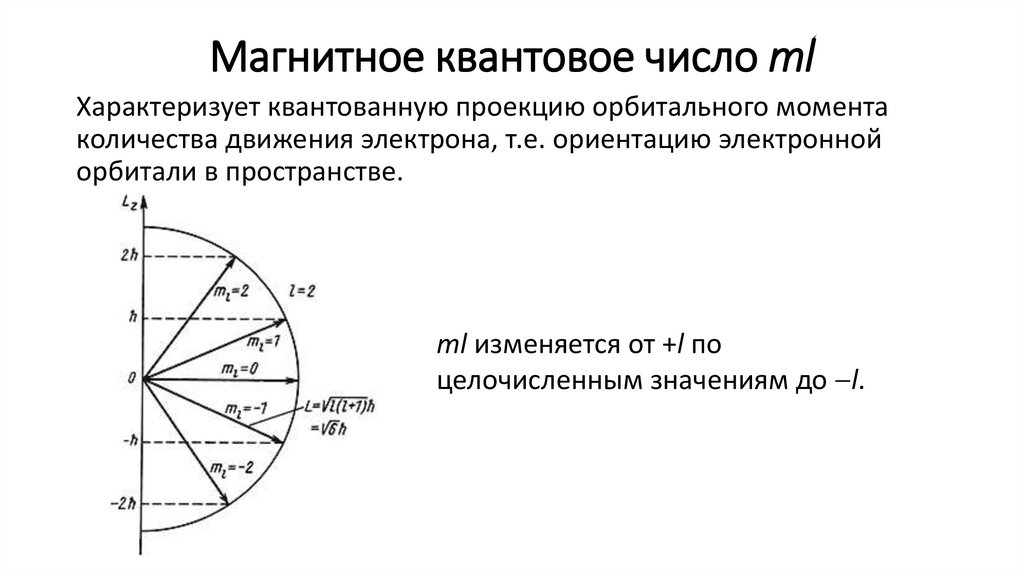
Магнитное квантовое число mlХарактеризует квантованную проекцию орбитального момента
количества движения электрона, т.е. ориентацию электронной
орбитали в пространстве.
ml изменяется от +l по
целочисленным значениям до l.
21.
Спиновое квантовое число msХарактеризует собственный момент количества движения электрона.
Для каждой элементарной частицы спин может принимать
единственное, присущее этому типу частиц значение.
Спины π-мезонов и К-мезонов равны 0. Спины электрона, протона,
нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1.
22.
Полный момент количества движенияэлектрона
Спин-орбитальное взаимодействие
Квантовое число полного момента j, соответствующее сумме двух
векторов l и s, может принимать ряд дискретных значений,
отличающихся на 1.
Проекция j на выделенную ось также принимает дискретные
значения: j, j 1,…, j+1, j. Число значений проекции на ось Jz равно















 chemistry
chemistry








