Similar presentations:
Логарифм числа. Десятичный и натуральный логарифмы, число е
1.
Тема:Логарифм числа.
Десятичный и
натуральный
логарифмы, число е
2. Решите уравнение.
1)Мы искали
х показатель степени,
Решить
а надо
в, где
а 0основание
и а 1, b0,5 ,0
0,5х =32,уравнение
в который
возвести
х = - 5.
чтобы получить 32.
значит, найти показательстепени,
2)
х
в который
надоМы
возвести
основание
a,
искали показатель
степени,
1
27, в который надо возвести основание 1 ,
3
чтобы
число
b
3 получить
чтобы получить 27.
х 3.
3)
Показатель
– это
и есть логарифм
4х+1+4х = 320степени
, Мы искали
показатель степени,
(при
определенных
условиях).
4х(4+1)
= 320
, в который надо возвести
основание 4,
4х = 64 ,
чтобы получить 64.
х = 3.
3.
Определение.Логарифмом числа b (b > 0) по
основанию a ( a > 0, a 1) называется
показатель степени c, в которую нужно
возвести основание a, чтобы получить
число b , т.е. если ac = b , то можно
записать logab = c .
Действие нахождения логарифма числа
называют логарифмированием.
4.
• Шотландскийматематик,
изобретатель логарифмов.
• Учился в Эдинбургском университете.
Основными
идеями
учения
о
логарифмах Непер овладел не позднее
1594 г., однако его "Описание
удивительной таблицы логарифмов",
в котором изложено это учение, было
издано в 1614 г.
• В этом труде содержались определение
логарифма, объяснение их свойств,
таблицы
логарифмов
синусов,
косинусов, тангенсов и приложения
логарифмов
в
сферической
тригонометрии.
• В "Построении удивительной таблицы
логарифмов" (опубликовано в 1619)
Непер изложил принцип вычисления
таблиц.
Непер Джон
(1550 - 1617)
5. Примеры
log 2 83 , т.к.
2 8
log 5 25 2 , т.к.
5 25
log 2 2
1 , т.к.
2 2
1
log 2 1, т.к.
2
1
2
2
1
2
3
9
1
log 3
9
2 , т.к.
3
2
1
1
6. Взаимосвязь операции возведения в степень и логарифмирования
• Возведение в степень• Логарифмирование
7 49;
log 7 49 2.
10 1000;
log 10 1000 3.
0,2 0,0032;
log 0, 2 0,00032 5.
1
3
5
;
125
1
log 5
3 .
125
2
3
5
7. Запишите в виде логарифмического равенства:
3 81log 3 81 4
(по определению);
1
2
32
1
log 2
5
32
(по определению);
3
1
log 1
3
64
4
4
5
1
1
64
4
3
125 5
4
16 8
3
1
log125 5
3
3
log16 8
4
8. Найдите число x
log 5 x 22
25
x 5
log 3 x 1
1
xx 31
3
log 1 x 2
6
2
1 2
x
6
xx 36
6
log 5 x 0
51
x
x
0
9. Найдите число x
log x 81 4x 3
4
3 81
1
log x
2
16
log 1 x 2
1
log x 2
4
6
2
1 2
x
6
xx 36
6
2
1
1
x
x
44
1
2x
2 4
2
10.
Основное логарифмическое тождество.c
a =b
logab = c
Откуда получаем основное
логарифмическое тождество
(b > 0, a > 0, a 1)
a
loga b
b
11.
Примеры.log0,5 6
1) 0,5
2)
5
5
2log5 3
log5 3
6 .
(( 5 ) )
3.
2 log5 3
12. Свойства, следующие из определения логарифма:
• 1.log a a 1;
a a.
• 2.
log a 1 0;
a 1.
• 3.
log a a c;
a a .
c
1
0
c
c
13.
• Десятичным логарифмомназывается логарифм по основанию
10. Он обозначается lg , т.е. log 10 m =
lg т
• Натуральным логарифмом
называется логарифм по основанию е.
Он обозначается ln , т.е. log e m = ln m.
Число е является иррациональным, его
приближённое значение 2.718281828.
14.
Десятичный логарифм• lg 1 = 0, так как 1 = 100
• lg 10 = 1 , так как 10 = 101
• lg 100 = 2, так как 100 = 102
• lg 0,1 = -1, так как 0,1 = 10-1
• lg 0,01 = -2, так как 0,01 = 10-2
• lg 0,001 = -3, так как 0,001 = 10-3
15.
Натуральный логарифм16.
• Первое упоминание натуральногологарифма сделал Николас Меркатор в
работе Logarithmotechnia,
опубликованной в 1668 году, хотя
учитель математики Джон Спайделл
ещё в 1619 году составил таблицу
натуральных логарифмов. Ранее его
называли гиперболическим
логарифмом, поскольку он
соответствует площади под гиперболой
17. е=2,718281828459045235360….
е=2,718281828459045235360….
Саму константу впервые вычислил
швейцарский математик Бернулли в
ходе решения задачи о предельной
величине процентного дохода.
Бернулли показал, что процентный
доход в случае сложного процента
имеет предел:
и этот
предел равен 2,71828…
Экспоненту помнить способ есть простой:
два и семь десятых, дважды Лев Толстой(1828)
2,7 1828 1828
18.
• Букву e начал использовать Эйлер в1727 году, а первой публикацией с этой
буквой была его работа «Механика, или
Наука о движении, изложенная
аналитически» 1736 год
• Почему была выбрана именно буква e,
точно неизвестно. Возможно, это
связано с тем, что с неё начинается
слово exponential («показательный»,
«экспоненциальный»). Другое
предположение заключается в том, что
буквы a, b, c и d уже довольно широко
использовались в иных целях, и e была
первой «свободной» буквой.










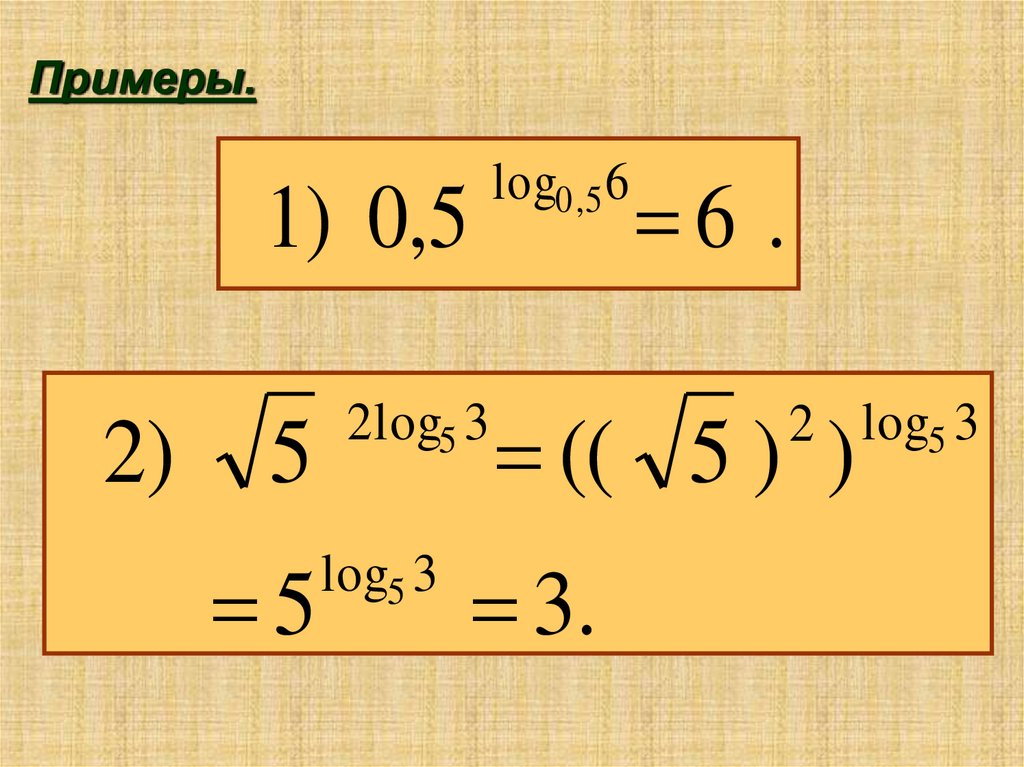







 mathematics
mathematics








