Понятие корня n- й степени из действительного числа

1.

Понятие корня n-й степени
из действительного числа

2.

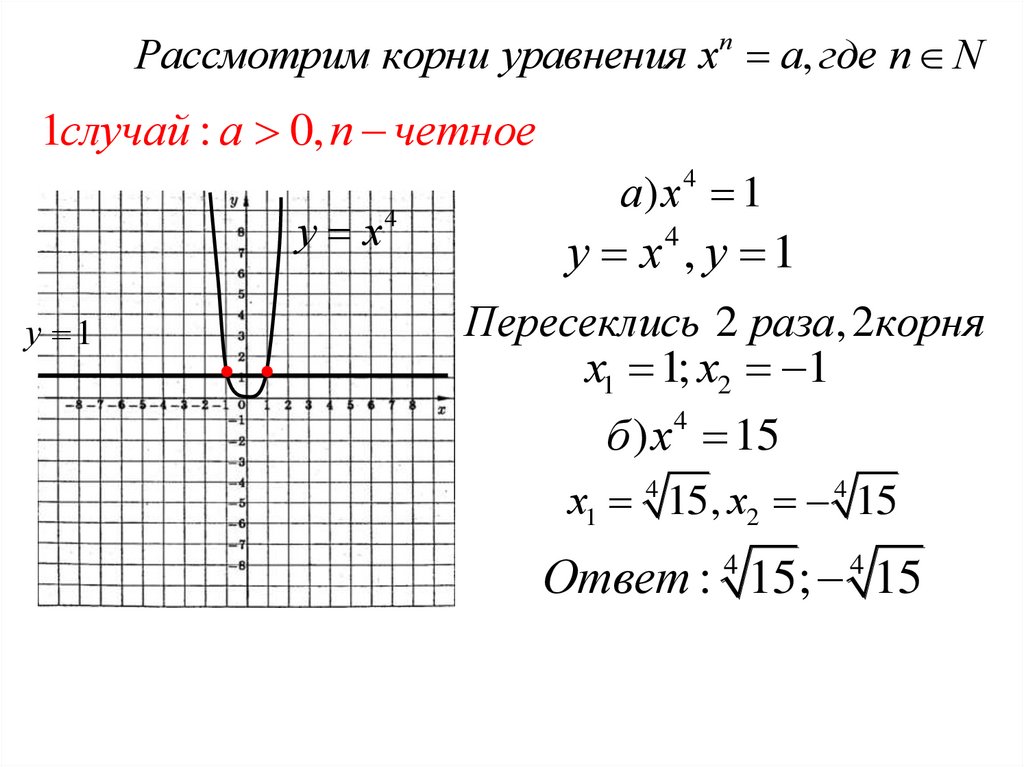
Рассмотрим корни уравнения хп а, где п N
1случай : а 0, п четное
у х
у 1
4
а) х 4 1
у х , у 1
4
Пересеклись 2 раза, 2корня
х1 1; х2 1
б ) х 15
4
х1 4 15, х2 4 15
Ответ : 15; 15
4
4

3.

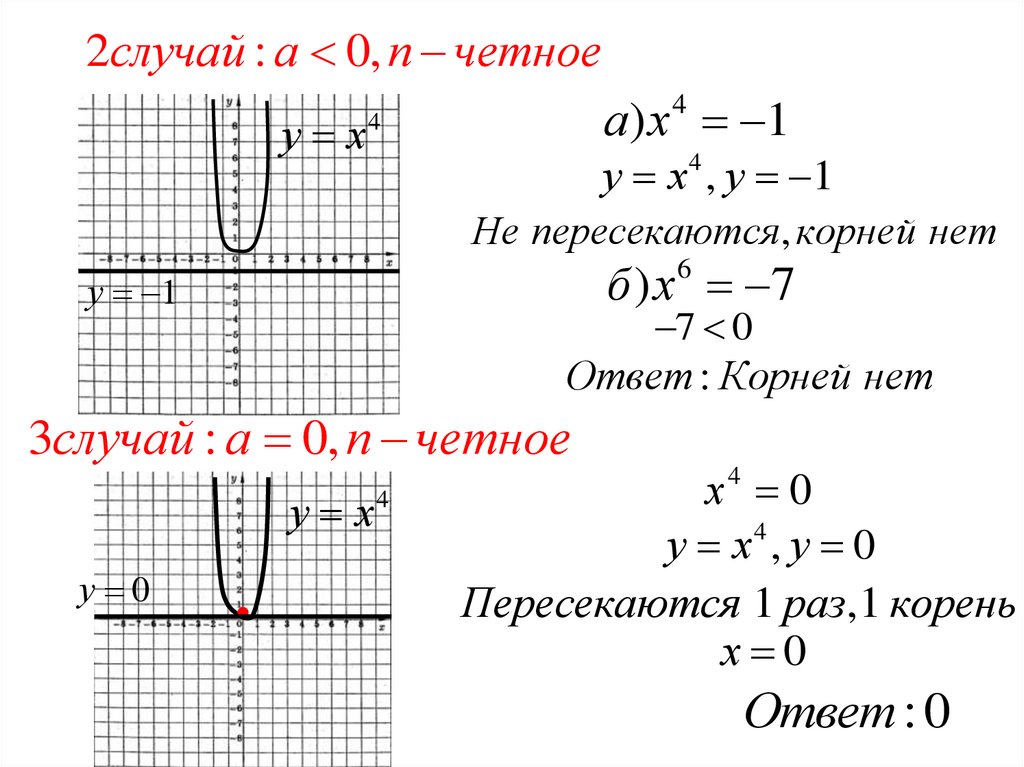
2случай : а 0, п четное
у х
а) х 4 1
4
у х 4 , у 1
Не пересекаются, корней нет
б ) х 7
6
у 1
7 0
Ответ : Корней нет
3случай : а 0, п четное
у х4
у 0
х4 0
4
у х ,у 0
Пересекаются 1 раз,1 корень
х 0
Ответ : 0

4.

При решении уравнения х а, где п четное, п N
п
если а 0 2 корня х1 п а , х2 п а
если а 0 1 корень х 0
если а 0 корней нет

5.

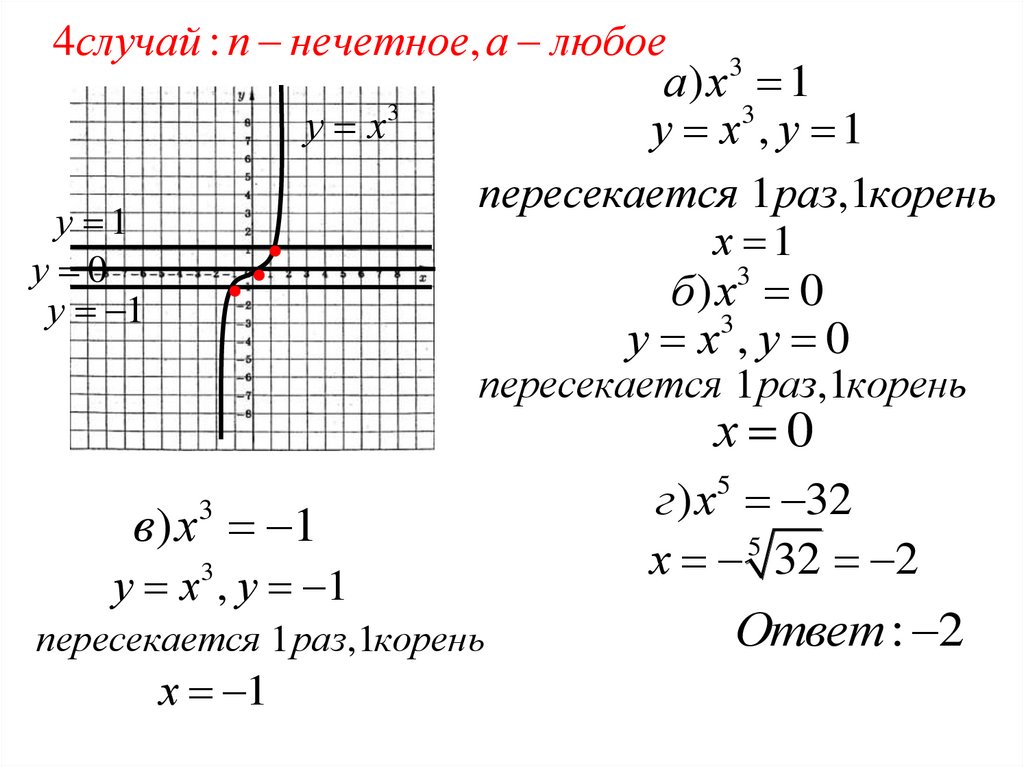
4случай : n нечетное, а любое 3
а) х 1
3
у х3
у х , у 1
пересекается 1 раз,1корень
у 1
х 1
у 0
3
б
)
х
0
у 1
3
у х ,у 0
пересекается 1 раз,1корень
х 0
в) х 1
3
у х , у 1
3
пересекается 1 раз,1корень
х 1
г ) х 32
х 5 32 2
5
Ответ : 2

6.

При решении уравнения х а, где п нечетное,
п
п N , а любое, уравнение имеет единственный
корень х п а
х3 10
х 3 10
Ответ : 3 10

7.

Корнем n-й степени из неотрицательного
числа а называют такое
неотрицательное число, которое при
возведении в степень n в результате
дает число а.
Корень n –й степени из отрицательного
числа существует, если n –нечетное.
а а
если а 0, то а 0 и а а
если а 0, то п а 0 и
п
п
п
п
п

8.

1) Вычислите :
5
32
3
0,125
4 5 1
16
2) Решите уравнение :
а) 3 3х 4 2
3х 4 8
3х 12
х 4
Ответ : 4
6
64
7
1
128
б ) 4 3х 2 1
1 0
3х 2 1
3х 3
х 1
Ответ :1

9.

в) 4 2 5 х 2 5
так как -5<0, то
корней нет
г ) 6 х 2 5 х 68 2
2 0
х 5 х 68 64
х2 5х 4 0
2
Ответ : корней нет
Д в 4ас 25 16 9 0(2к )
2
в Д 5 3
х1;2
2а
2
х1 4; х2 1
Ответ :1; 4.

10.

у х
n

11.

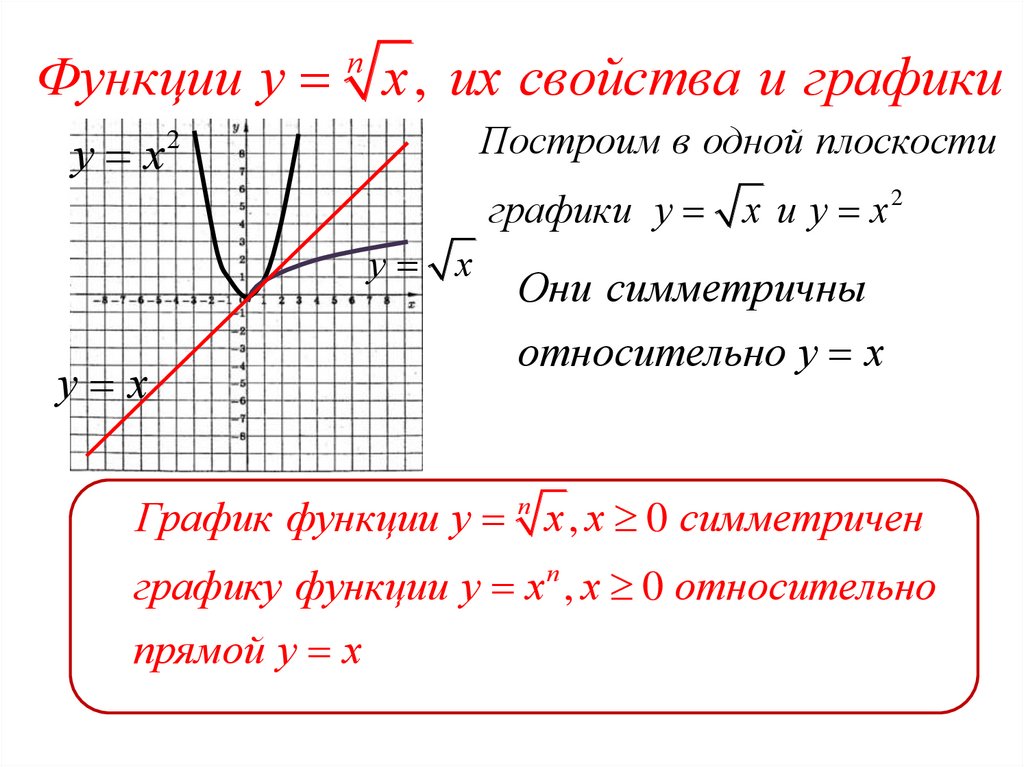
Функции у п х , их свойства и графики
Построим в одной плоскости
у х2
графики у х и у х 2
у х
у х
Они симметричны
относительно у х
График функции у п х , х 0 симметричен
графику функции у х п , х 0 относительно
прямой у х

12.

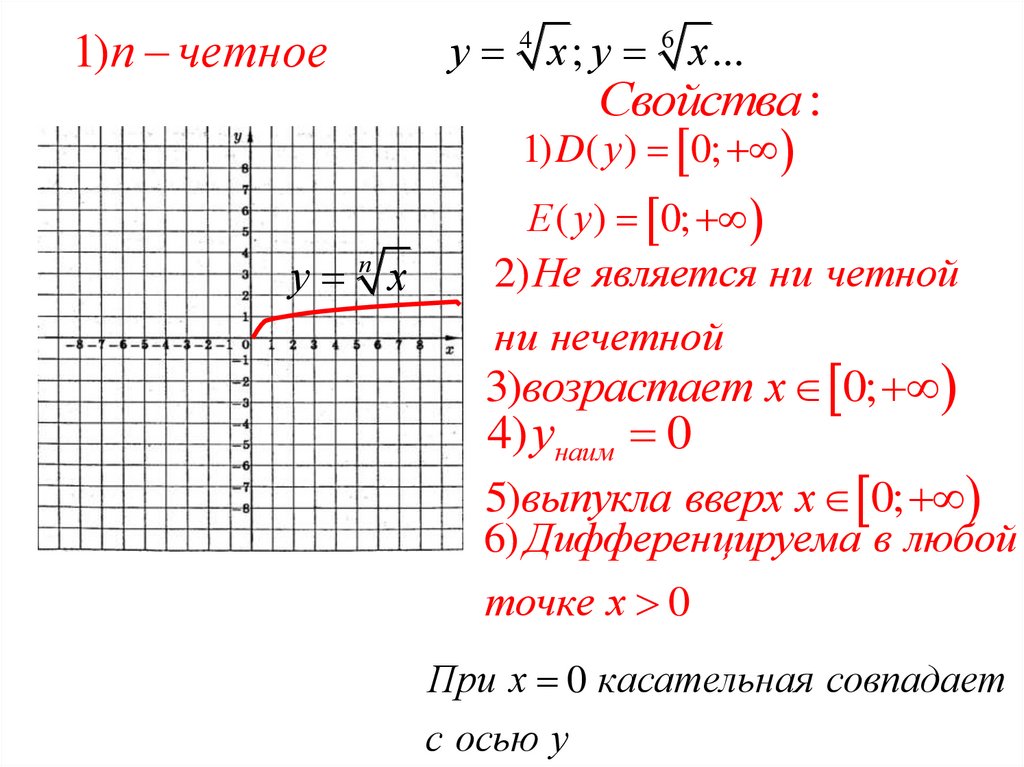
1)п четное
у 4 х ; у 6 х ...
Свойства :
1) D( у ) 0;
у п х
Е ( у ) 0;
2)Не является ни четной
ни нечетной
3)возрастает х 0;
4) унаим 0
5)выпукла вверх х 0;
6) Дифференцируема в любой
точке х 0
При х 0 касательная совпадает
с осью у

13.

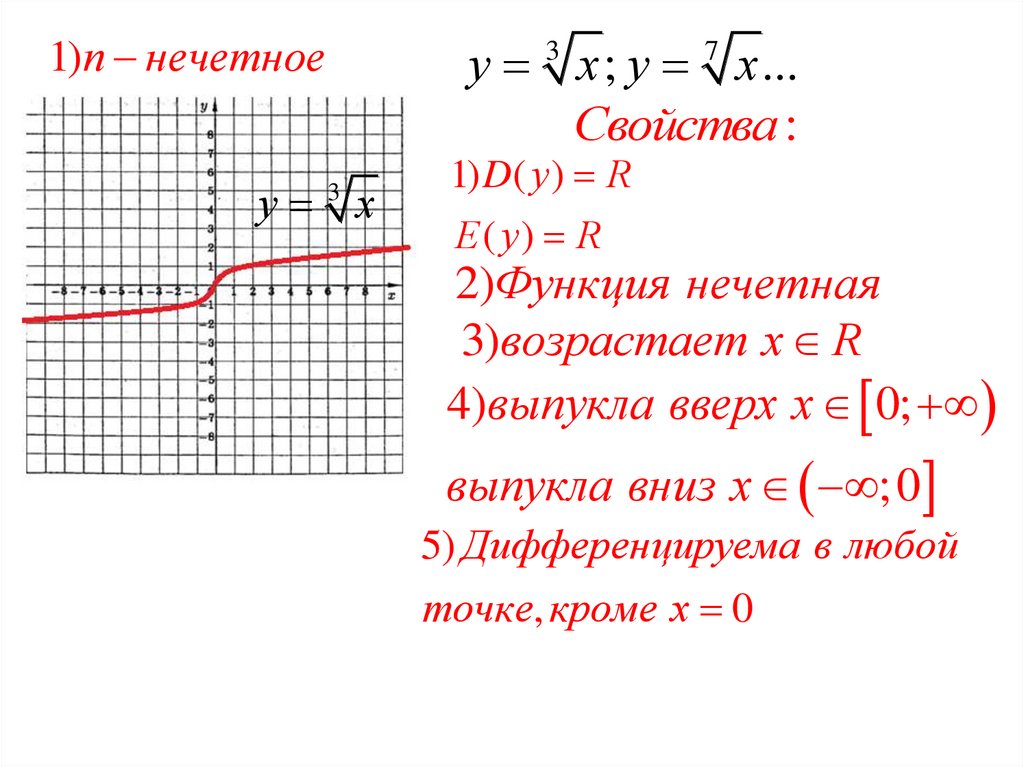
1)п нечетное
у х ; у х ...
Свойства :
3
у х
3
7
1) D( у ) R
Е ( у) R
2)Функция нечетная
3)возрастает х R
4)выпукла вверх х 0;
выпукла вниз х ;0
5) Дифференцируема в любой
точке, кроме х 0

14.

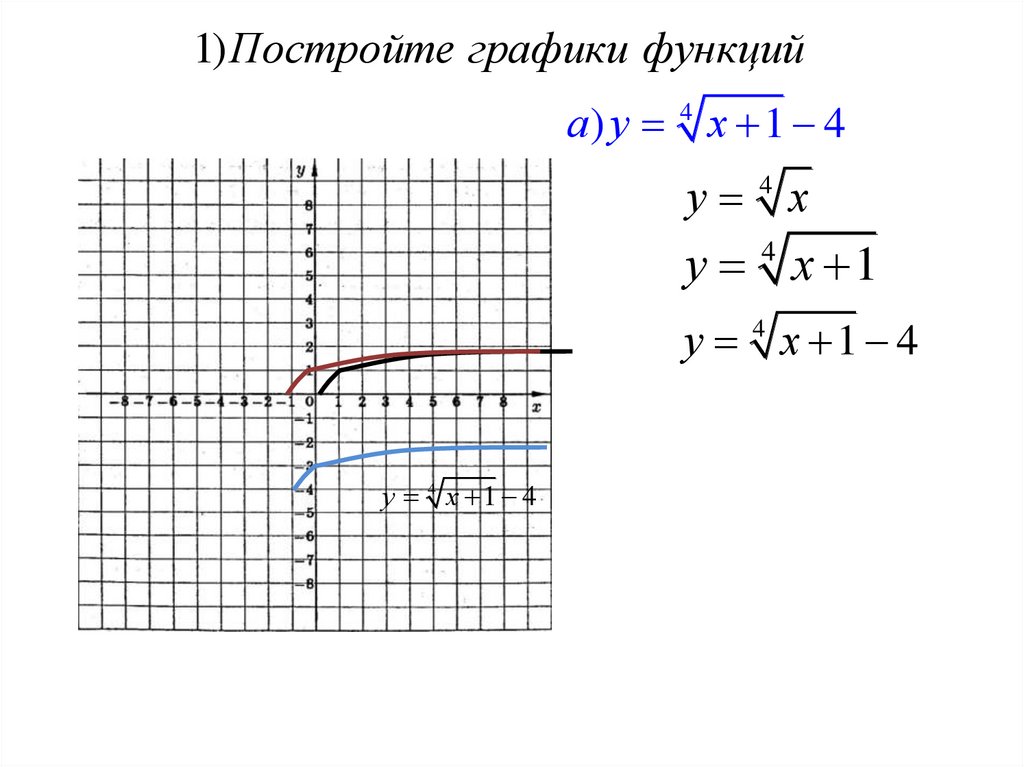
1)Постройте графики функций
а) у 4 х 1 4
у 4 х
у х 1
4
у 4 х 1 4
у 4 х 1 4

15.

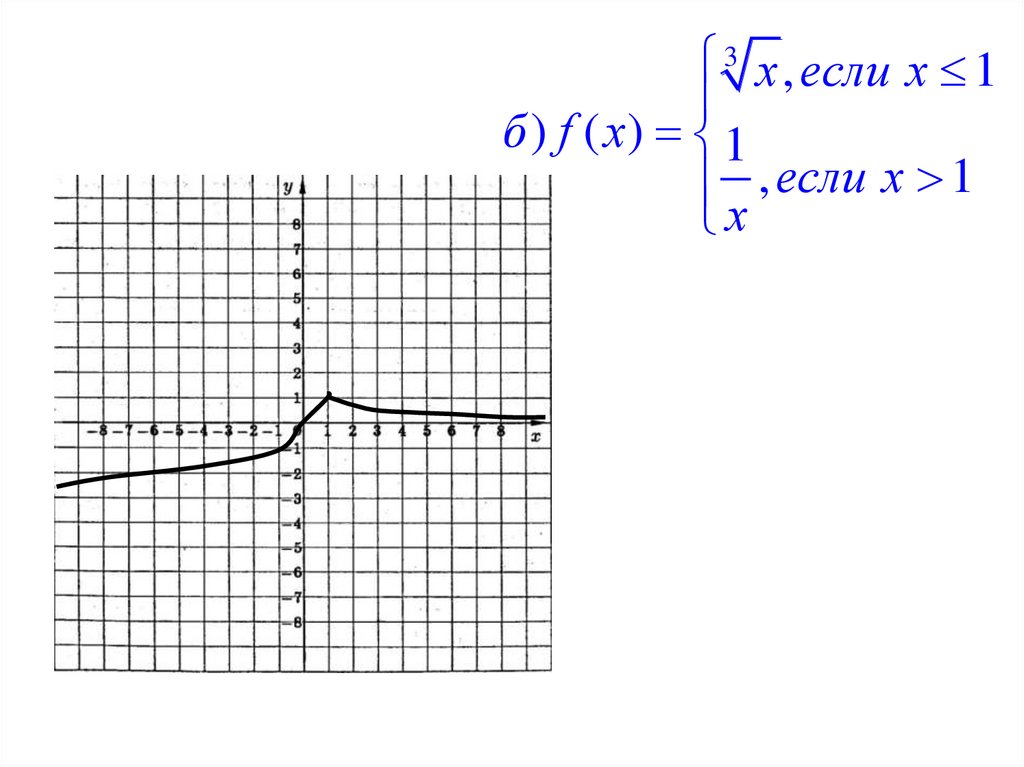
3 х , если х 1
б ) f ( х) 1
, если х 1
х

16.

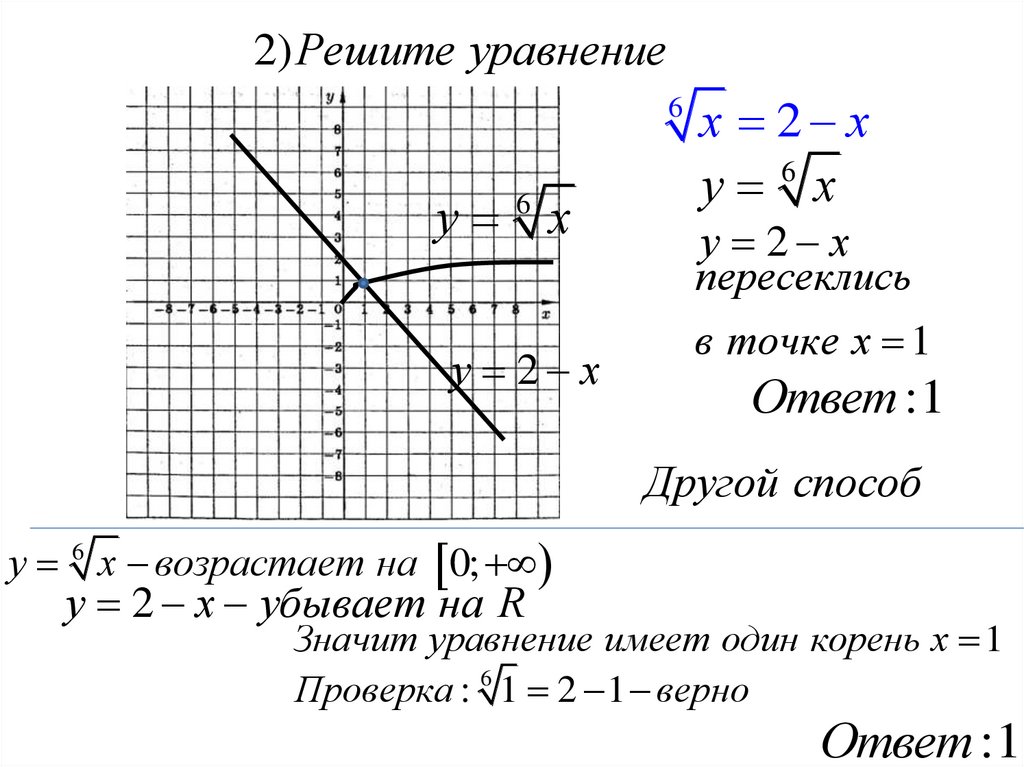
2)Решите уравнение
6
у х
6
у 2 х
х 2 х
у 6 х
у 2 х
пересеклись
в точке х 1
Ответ :1
Другой способ
у 6 х возрастает на 0;
у 2 х убывает на R
Значит уравнение имеет один корень х 1
Проверка : 6 1 2 1 верно
Ответ :1

17.

3)Найти область определения функции
а) у 4 х 8
4
Выражение 4 4 х 8 имеет смысл, если
4х -8 0
4х 8
х 2
Ответ : D( у) 2;
б) у х 9
Выражение 3 х 2 9 определено всегда
3
2
Ответ:D(у)=R

18.

в) у 6 16 х 2 2 х 2
Данная функция определена , если
1)2 х 2 0
2 х 2 0
2
16
х
0
2х 2
х 1 х 1;
2)16 х 0
2
Рассмотрим функцию z=16 х квадратичная
График парабола, ветви направлены вниз
2
Ее нули х 4
-4
4
х
х 4;4
3)найдем решение системы

19.

Домашнее задание
• Учебник ( розовый) стр. 31-40 читать, учить
понятия
• Задачник стр 30
• № 4.7, 9, 11, 12, 21
• Стр 32
• № 5(а,в), 6 (а,б), 13(б), 14(б), 15(а)