Similar presentations:
Гибкость макромолекул
1.
Гибкость макромолекулГибкость цепи – способность цепи изменять форму под
влиянием теплового движения звеньев или
внешнего поля, в котором полимер помещен
Начальные представления о полимерах :
макромолекулы - жесткие палочкообразные частицы, что не
позволяло объяснить причины высокоэластичного состояния
полимеров
Современные представления :
Макромолекулы обладают гибкостью за счет внутреннего
вращения атомных групп вокруг σ – связей ( С – С, С – О и др.)
Доказательство:
замещенные этилена существуют в двух геометрических
формах (цис-, транс- изомеры), что не характерно для
замещенных этана.
2.
Наличиевнутреннего
вращения
приводит
возникновению различных конформаций макромолекул.
к
Изменение формы молекул под действием теплового
движения при излучении, не сопровождающееся разрывом
химических связей называется конформационными
превращениями.
Формы молекул, переходящие друг в друга без разрыва
химических связей, т.е. без изменения конфигураций,
называются
конформациями
или
поворотными
изомерами.
Эти понятия были введены Марком, Куном и Гутом.
3.
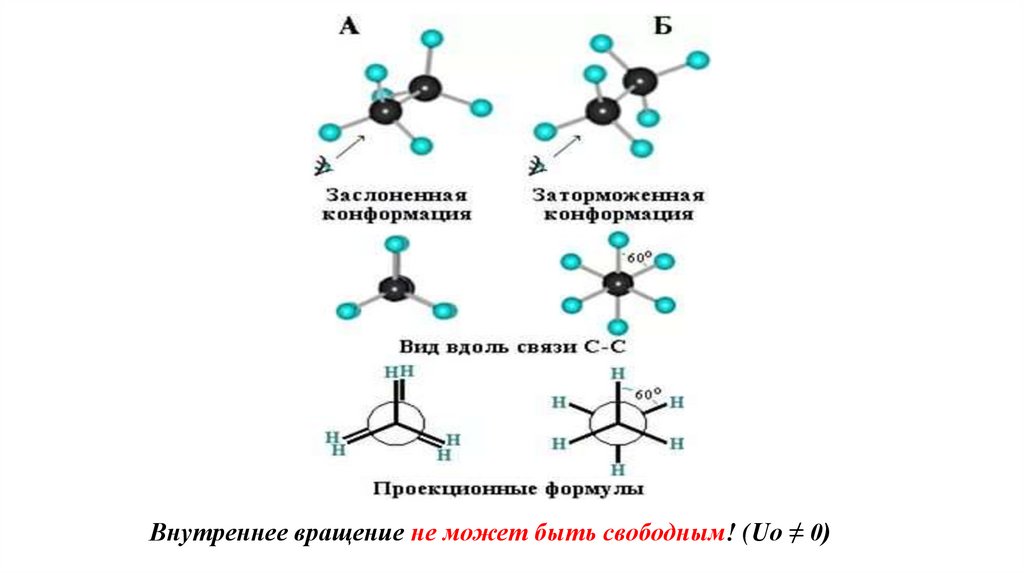
Внутреннее вращение не может быть свободным! (Uo ≠ 0)4.
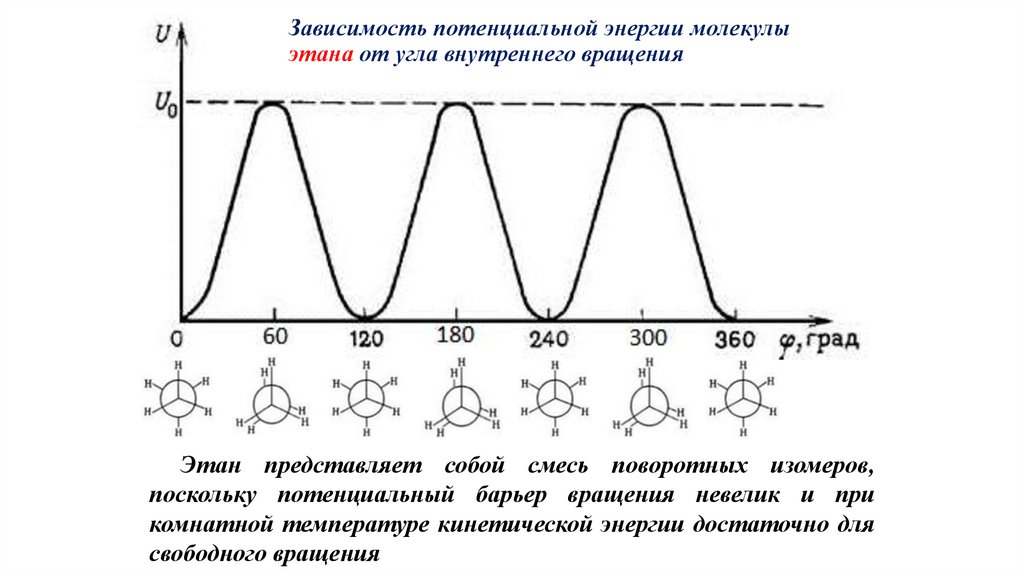
Зависимость потенциальной энергии молекулыэтана от угла внутреннего вращения
Этан представляет собой смесь поворотных изомеров,
поскольку потенциальный барьер вращения невелик и при
комнатной температуре кинетической энергии достаточно для
свободного вращения
5.
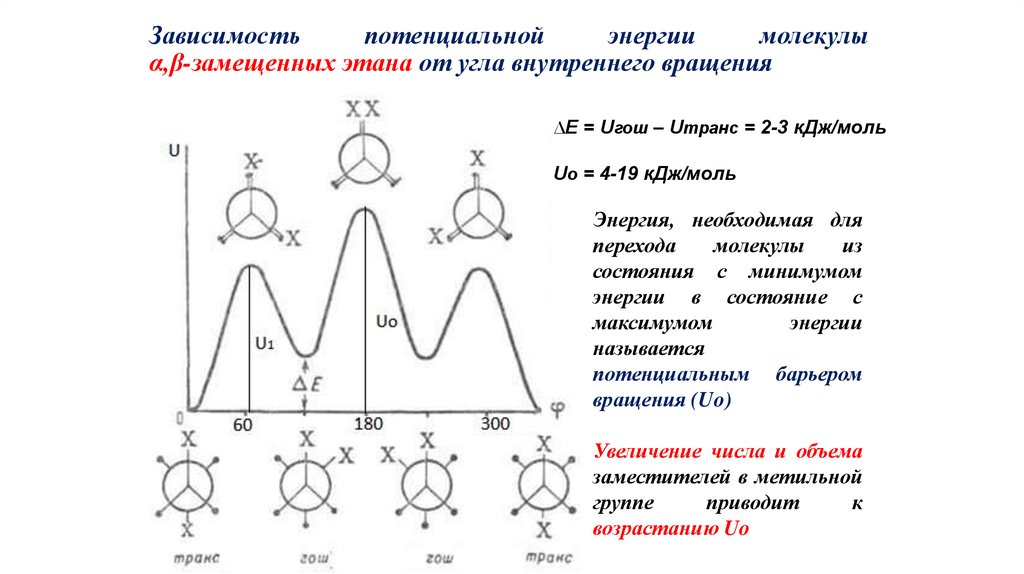
Зависимостьпотенциальной
энергии
молекулы
α,β-замещенных этана от угла внутреннего вращения
∆E = Uгош – Uтранс = 2-3 кДж/моль
Uo = 4-19 кДж/моль
Энергия, необходимая для
перехода
молекулы
из
состояния с минимумом
энергии в состояние с
максимумом
энергии
называется
потенциальным барьером
вращения (Uo)
Увеличение числа и объема
заместителей в метильной
группе
приводит
к
возрастанию Uo
6.
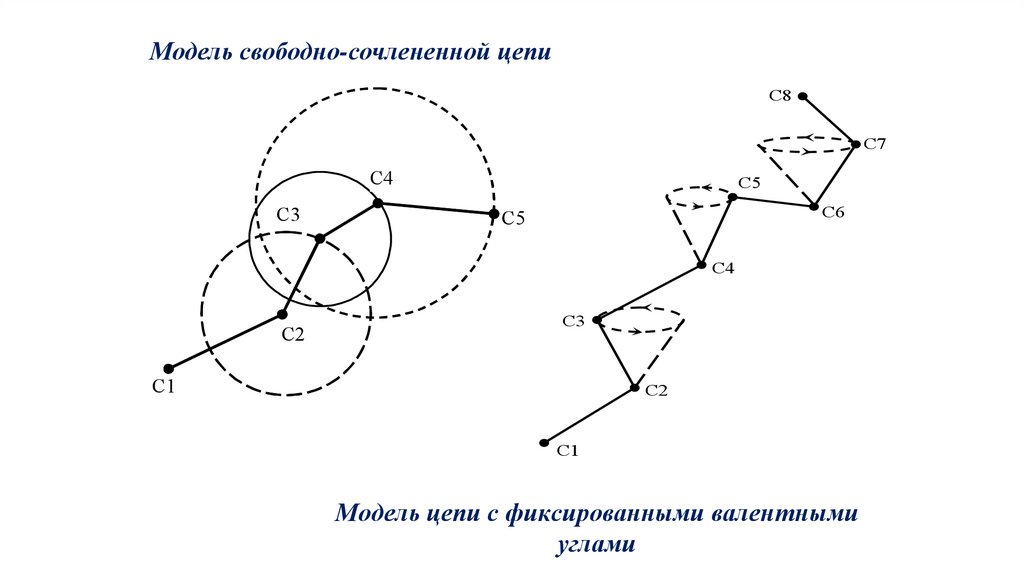
Модель свободно-сочлененной цепиС8
С7
С4
С3
С5
С6
С5
С4
С2
С3
С1
С2
С1
Модель цепи с фиксированными валентными
углами
7.
Рассмотрим модели гибкости цепиУчасток цепи, состоящий из нескольких атомов углерода, соединенных между собой σ – связями, причем
валентные углы в такой гипотетической цепи не фиксированы, а внутреннее вращение свободно. Геометрическим
мостом атома С3 будет поверхность сферы радиусом С2-С3, а положение звена С2-С3 в пространстве
произвольно. Геометрическим местом атома С4 является уже поверхность бесконечного множества сфер,
геометрическим
местом
центров
которых
является
сфера
радиусом
С2-С3
и
т.д.
И так, такая цепь является предельно гибкой и называется свободно-сочлененной и может принимать любые
конформации. Положение ее звеньев в пространстве произвольно и не зависит от положения соседних.
Но в реальных макромолекулах валентные углы фиксированы и пространственные расположения звеньев
взаимозависимы. При свободном вращении число конформаций такой цепи ограничено и много меньше, чем у
свободно сочлененной. Тем не менее она может сильно изгибаться – это модель с фиксированными валентными
углами (или со свободным вращением)
Геометрическим местом звена С2-С3 и атома С3 являются поверхность конуса и окружность, лежащая в
основании, соответственно. Для звена С3-С4 и атома С4 это будет уже поверхность бесконечного множества
конусов с вершинами, лежащими на окружности и окружности, лежащие в их основании.
Однако и эта модель реально не отражает ситуацию. Внутренне вращение не бывает свободным (торможение
за счет несвязанных атомов). Такое взаимодействие бывает внутри- и межмолекулярным. Последнее трудно
учитывать. Внутримолекулярное подразделяют на взаимодействия ближнего и дальнего порядка (от далеко
отстоящих атомов).
Поэтому реальная цепь из-за внутримолекулярного взаимодействия еще менее гибкая, чем цепь со
свободным вращением и принимает еще меньшее число конформаций.
8.
Фрагментпотенциальной кривой
Термодинамическая гибкость
определяется разностью
потенциальных энергий 2-х
конформаций звена.
ΔU = Uгош – Uтранс
Термодинамическая гибкость характеризует гибкость цепи при равновесии и
дает представление о способности цепи к конформационным переходам.
Скорость перехода из одной конформации в другую зависит от соотношения
между энергии звена и высотой потенциального барьера (Uo). Величина Uo
определяет кинетическую гибкость цепи.
Термодинамическая и кинетическая гибкость в общем не совпадает.
9.
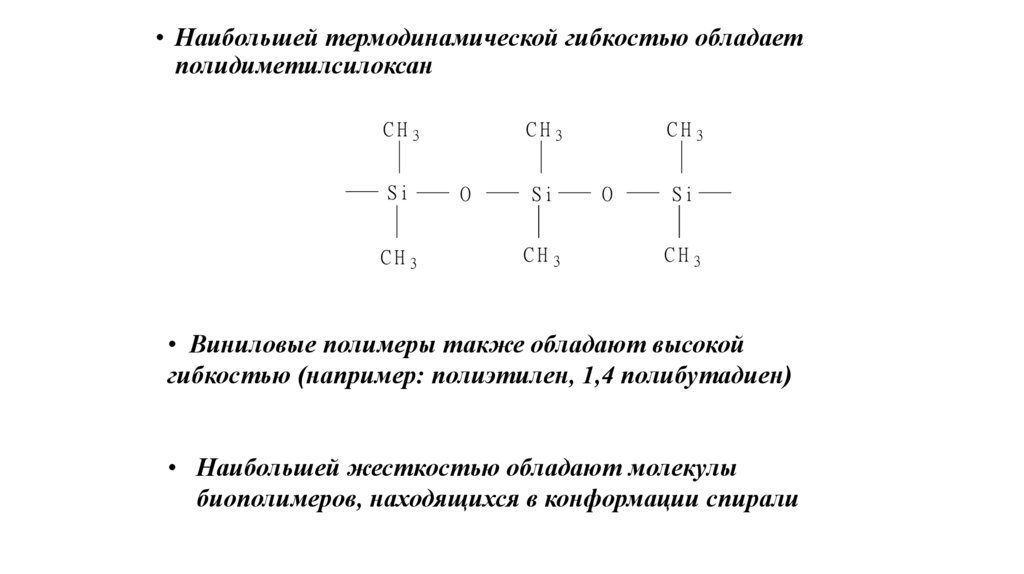
• Наибольшей термодинамической гибкостью обладаетполидиметилсилоксан
CH 3
Si
CH3
CH 3
O
Si
CH 3
CH 3
O
Si
CH3
• Виниловые полимеры также обладают высокой
гибкостью (например: полиэтилен, 1,4 полибутадиен)
• Наибольшей жесткостью обладают молекулы
биополимеров, находящихся в конформации спирали
10.
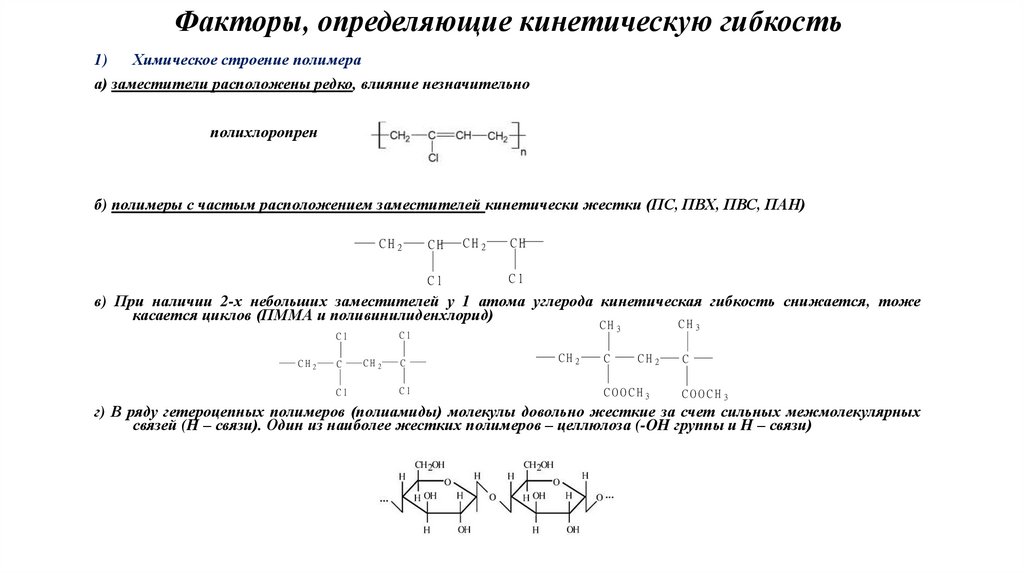
Факторы, определяющие кинетическую гибкость1)
Химическое строение полимера
а) заместители расположены редко, влияние незначительно
полихлоропрен
б) полимеры с частым расположением заместителей кинетически жестки (ПС, ПВХ, ПВС, ПАН)
CH2
CH
Cl
CH 2
CH
Cl
в) При наличии 2-х небольших заместителей у 1 атома углерода кинетическая гибкость снижается, тоже
касается циклов (ПММА и поливинилиденхлорид)
CH
CH2
C
Cl
CH 3
Cl
Cl
CH 2
C
Cl
CH 2
C
3
CH 2
COOCH 3
C
COOCH 3
г) В ряду гетероцепных полимеров (полиамиды) молекулы довольно жесткие за счет сильных межмолекулярных
связей (H – связи). Один из наиболее жестких полимеров – целлюлоза (-OH группы и H – связи)
11.
2) Молекулярная массав полимер – гомологическом ряду молекулярная масса не влияет на Uo.
Однако, число возможных конформаций молекул находится в прямой зависимости
от степени полимеризации (n). При очень большой степени полимеризации
полимеры, обладающие высоким потенциальным барьером сворачиваются
3) Частота пространственной сетки
Гибкость цепей полимера с редкой пространственной сеткой остается
практически неизменной. С увеличением числа сшивок гибкость уменьшается
4) Температура
Изменение температуры практически не влияет на Uo.
Однако с повышением температуры увеличивается энергия молекул и
появляется бόльшая возможность преодолеть барьер. Скорость поворотов звеньев
и интенсивность их колебаний возрастает, следовательно, увеличивается
гибкость.





 chemistry
chemistry








