Similar presentations:
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
1.
УРОК – ПРЕЗЕНТАЦИЯ.ТЕМА : Определение
геометрической прогрессии.
Формула n-го члена
геометрической прогрессии
2.
ЦЕЛЬ УРОКА :Формирование понятия геометрической
прогрессии, используя сопоставление и
противопоставление понятию арифметической
прогрессии.
Знакомство со свойствами геометрической
прогрессии и формулой n–ого члена,
Определение геометрической прогрессии,
выведение формулы n–ого члена,
применение этой формулы и свойства на
примерах и задачах.
3.
Изучение понятиягеометрической
прогрессии и вывод
формулы n-го члена
геометрической
прогрессии.
4.
• "Прогрессия" – латинское слово,означающее "движение вперед",
было введено римским автором
Боэцием (VI век) и понималось в
более широком смысле, как
бесконечная числовая
последовательность
5.
Геометрической прогрессиейназывается
последовательность отличных от
нуля чисел, каждый член которой,
начиная со второго, равен
предыдущему члену, умноженному
на одно и тоже число.
6.
О прогрессии известно так давно, что конечнонельзя говорить о том, кто их открыл это и
понятно – ведь уже натуральный ряд 1,2,3,4…n…
есть арифметическая прогрессия.
О том, как давно известна геометрическая
прогрессия, косвенным образом свидетельствует
знаменитое предание о создании шахмат.
7.
Немного ИсторииСамой известной древней задачей на прогрессии считается
задача об изобретении шахмат. В древней Индии ученый
Сета изобрел шахматы и попросил у шаха Шерама в награду
за свое изобретение столько пшеничных зерен, сколько их
получится, если на первую клетку шахматной доски
положить одно зерно, на вторую - в 2 раза больше, то есть
2 зерна, на третью - еще в 2 раза больше, то есть 4 зерна, и
так далее до шестьдесят четвертой клетки. Сначала
индийский царь обрадовался, что дешево отделался, и лишь
потом выяснил, что такого количества пшеницы нельзя
собрать со всех полей Земли в течение десятков лет. Вот
это число:
18 446 744 073 709 551 615.
8.
9.
10.
Для того чтобы подсчитатьвеличину награды,
надо сложить зерна, лежащие
на всех клеточках доски.
1 2 2 2 2
2
2
3
4
63
11.
12.
ОпределениеЧисловая
последовательность, в
которой каждый
следующий член
получается из
предыдущего
прибавлением одного и
того же числом
d,называется
арифметической
прогрессией.
Числовая
последовательность
отличных от нуля
чисел, в которой
каждый следующий
член получается из
предыдущего
умножением на одно
и тоже число q,
называется
геометрической
прогрессией.
13.
Число d –называется
разностью
Число q –
называется
знаменателем
арифметической геометрической
прогрессии.
прогрессии.
14.
ОбозначениеАрифметическая
прогрессия
Геометрическая
прогрессия
a
n
b
n
15.
Допустимые значенияАрифметическая
прогрессия
Геометрическая
прогрессия
a1 , d
,
b1 q
любые числа
числа неравные
нулю
16.
Рекуррентная формулаАрифметическая
прогрессия
Геометрическая
прогрессия
an 1 an d
bn 1 bn q
n N
n N
17.
Нахождениеразность
арифметической
прогрессии
d a n 1 a
n
знаменатель
геометрической
прогрессии
q
bn 1
b
n
n N
n N
18.
Используя рекуррентную формулу,получим формулу общего члена
геометрической прогрессии.
b b q
b b q b q q b q
b b q b q q b q
2
3
1
2
1
1
2
4
3
1
b b q b q q b q
4
1
3
1
3
5
2
1
4
19.
Итак,bn b1 b
n 1
20.
Формула n-го членаарифметическая
прогрессия
геометрическая
прогрессия
an a1 d n 1 bn b1 b
n N
n N
n 1
21.
Характеристическоесвойство
арифметическая
прогрессия
геометрическая
прогрессия
b b
2
a
n
an 1 an 1
2
n N
n
n 1 bn 1
или
b b b
n
n 1
n N
n 1
22.
Спасибо за урок!!!До новых встреч!


















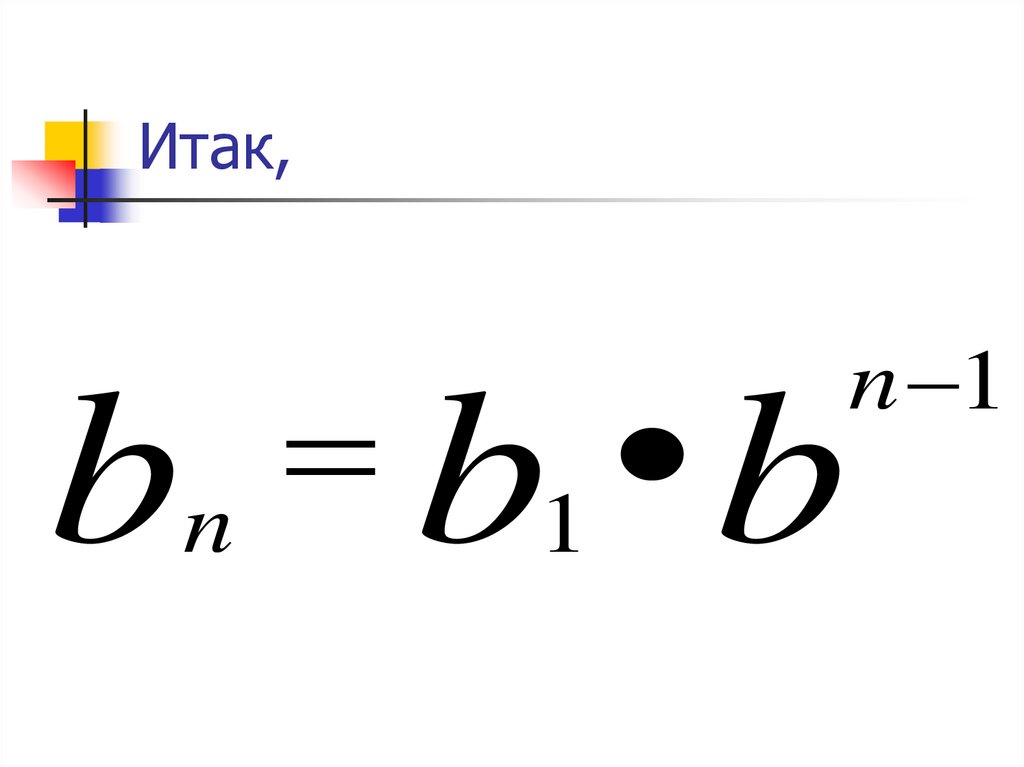



 mathematics
mathematics








