Similar presentations:
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
1. УРОК – ПРЕЗЕНТАЦИЯ. ТЕМА : Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
Для добавления текстащёлкните мышью
2. Изучение понятия геометрической прогрессии и вывод формулы n-го члена геометрической прогрессии.
Изучение понятиягеометрической
прогрессии и вывод
формулы
n-го
члена
Для добавления текста щёлкните
геометрической
мышью
прогрессии.
3. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен
предыдущему члену, умноженномуна одно и тоже число.
4. Определение
Числоваяпоследовательность, в
которой каждый
следующий член
получается из
предыдущего
прибавлением одного и
того же числом
d,называется
арифметической
прогрессией.
Числовая
последовательность
отличных от нуля
чисел, в которой
каждый следующий
член получается из
предыдущего
умножением на одно
и тоже число q,
называется
геометрической
прогрессией.
5.
Число d –называется
разностью
Число q –
называется
знаменателем
арифметической геометрической
прогрессии.
прогрессии.
6. Обозначение
Арифметическаяпрогрессия
a
n
Геометрическая
прогрессия
b
n
7. Допустимые значения
Арифметическаяпрогрессия
a1 , d
любые числа
Геометрическая
прогрессия
,
b1 q
числа неравные
нулю
8. Рекуррентная формула
Арифметическаяпрогрессия
Геометрическая
прогрессия
an 1 an d
bn 1 bn q
n N
n N
9. Нахождение
разностьарифметической
прогрессии
d a n 1 an
n N
знаменатель
геометрической
прогрессии
q
b
b
n N
n 1
n
10. Используя рекуррентную формулу, получим формулу общего члена геометрической прогрессии.
b b qb b q b q q b q
b b q b q q b q
b b q b q q b q
2
1
2
3
2
1
1
2
4
3
1
1
3
5
4
1
3
1
4
11. Итак,
bn
b1 b
n 1
12. Формула n-го члена
арифметическаяпрогрессия
геометрическая
прогрессия
an a1 d n 1 bn b1 b
n N
n N
n 1
13. Характеристическое свойство
арифметическаяпрогрессия
a
n
a
n 1
an 1
геометрическая
прогрессия
b
b
n
n 1 bn 1
2
или
2
n N
b
n
b b
n 1
n N
n 1
14. Решение задач
Для добавления текста щёлкнитемышью
15. Задача 1
Найдите первые 5 членовгеометрической прогрессии , если
первый член -2, а знаменатель -0.5.
Ответ: -2; 1; -0,5; 0,25; - 0,125
16.
17. Задача 3 (решить двумя способами)
Найдите знаменатель геометрическойпрогрессии, если ее четвертый член
25, а шестой член 16.
4
4
;
Ответ:
5
5
18. Задача 4.
1Между числами
и 27 вставьте
9
четыре числа, чтобы получилась
геометрическая прогрессия.
Найдите эти числа.
1
Ответ:
; 1; 3; 9
3
19. Задача 5.
Дана геометрическая прогрессия (bn),1
b
4
b5 216
в которой
и
b
2
b6 4
Найти первый член геометрической
прогрессии.
Ответ: 12 или
15
3
7










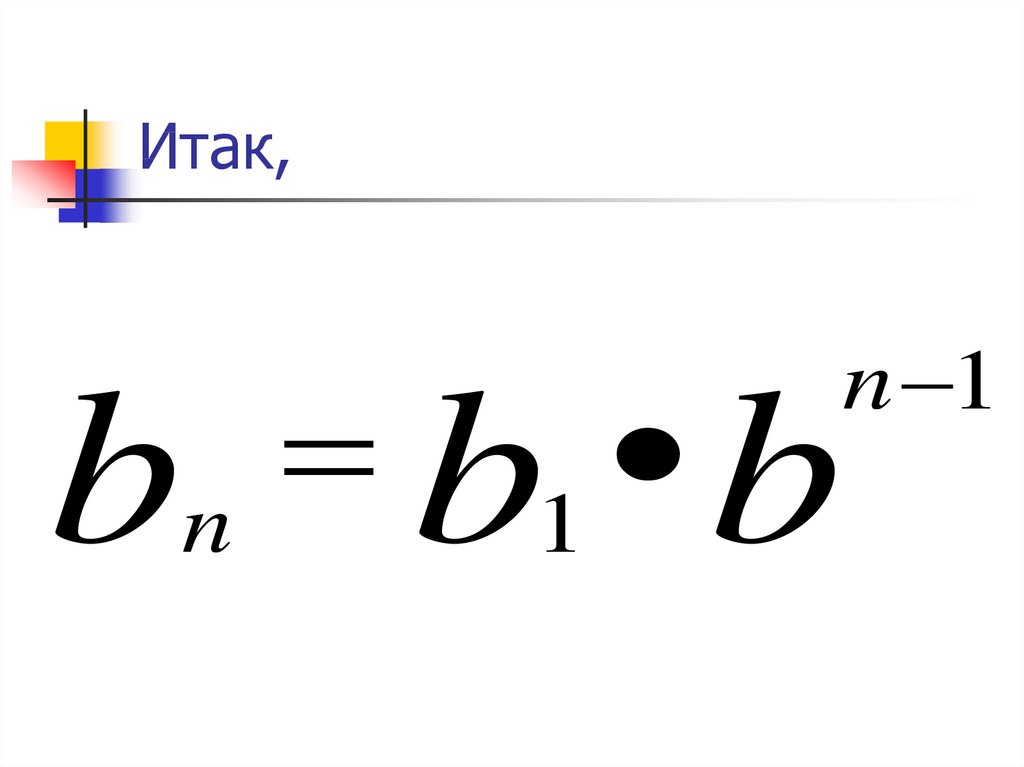








 mathematics
mathematics








