Программа расчёта параметров движения подвижного объекта с изменяющейся массой

1.

ДОКЛАД ПО ТЕМЕ:
«ПРОГРАММА РАСЧЁТА ПАРАМЕТРОВ
ДВИЖЕНИЯ ПОДВИЖНОГО ОБЪЕКТА С
ИЗМЕНЯЮЩЕЙСЯ МАССОЙ»
Подготовил:
Студент гр.132321
Поляков Л.В.
Научный руководитель
Шилин П.Д.

2.

Оглавление
1. Ведение
2. Цель
3. Физическая модель
4. Математическое обеспечение программного
продукта
5. Дополнительные уравнения и зависимости
6. Реализация программного продукта
7. Заключение
8. Список литературы

3.

Введение
Современные
технологии
позволяют
осуществить
переход
к
информационному обществу, в котором новые информационные технологии
глубоко проникают во все сферы хозяйства, производства, науки, образования,
во все направления интеллектуальной деятельности человека. Информация
становится важнейшим ресурсом развития общества.
В настоящее время, когда ЭВМ стала неотъемлемой частью научноисследовательских институтов, конструкторских бюро и т.д. , любой человек,
окончивший высшее учебное заведение, должен обладать знаниями и навыками,
необходимыми для решения задач ,применяя средства и возможности
современной вычислительной техники.
Создание инновационных объектов и устройств, разработка новых
технологических процессов возможна только на основе новейшей информации,
наиболее современных средств и методов обработки информации с
применением современных средств вычислительной техники и программных
средств.

4.

Цель
Исследовать влияние задержки времени отделения части
конструкции , а также влияние компоновки, на параметры
движения подвижного объекта изменяющейся массы.

5.

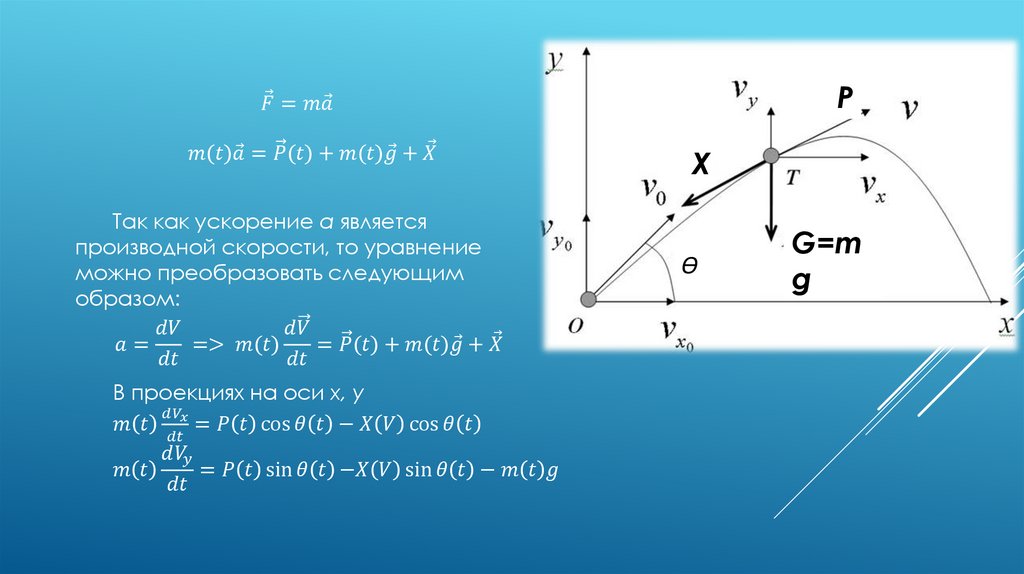
Физическая модель
На рисунке показана физическая модель
движения ЛА, согласно которой ЛА заменяем
материальной точкой, в которой приложены все
силы, действующие на него. Такой точкой является
центр масс. В произвольный момент времени на
ЛА действуют следующие силы: Р – сила тяги, Х
– сила лобового сопротивления, G=mg – сила
тяжести.
Р
Х
ϴ
G=m
g
ЛА запускается при следующих начальных условиях:
с земли (x0,y0)=(0,0) под углом θ=θ0 к горизонту со скоростью V=V0 в момент времени t = 0.

6.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ
С учетом принятых допущений центр масс
ракеты будет совершать поступательное движение
под действием сил, действующих в одной
плоскости: Методика расчета траектории базируется
на основном законе механики (втором законе
Ньютона), связывающем ускорение, испытываемое
точкой массой m под действием силы F: