Similar presentations:
Интегрирование. Лекция №4
1.
ИнтегрированиеРассмотрим функцию одной переменной.
F x ,
f x F x .
найти производную
Задача:
задана
Это операция – дифференцирование.
2.
ИнтегрированиеРассмотрим функцию одной переменной.
F x ,
f x F x .
найти производную
Задача:
задана
Это операция – дифференцирование.
Обратная задача (операция):
f (x), найти функцию,
производная от которой равна f (x),
т.е. F x .
Задана производная.
3.
ИнтегрированиеРассмотрим функцию одной переменной.
F x ,
f x F x .
найти производную
Задача:
задана
Это операция – дифференцирование.
Обратная задача (операция):
f (x), найти функцию,
производная от которой равна f (x),
т.е. F x .
Задана производная.
Эта обратная операция –интегрирование.
4.
Первообразная функцииОпределение. Пусть функция f x
задана на промежутке
X
.
5.
Первообразная функцииОпределение. Пусть функция f x
задана на промежутке
X
f x
и на этом промежутке
есть производная от функции F x
.
6.
Первообразная функцииОпределение. Пусть функция f x
задана на промежутке
X
f x
и на этом промежутке
есть производная от функции F x
F x f x
.
7.
Первообразная функцииОпределение. Пусть функция f x
задана на промежутке
X
f x
и на этом промежутке
есть производная от функции F x
F x f x
F x
.
называется первообразной функцией для
f x на промежутке X
8.
Примеры первообразных1.
f x 2x,
X , .
9.
Примеры первообразных1.
f x 2x,
X , .
2
F x x ,
2
G x x 6.
10.
Примеры первообразныхf x 2x,
X , .
2
F x x ,
2
G x x 6.
2. f x cos x
X ,
1.
11.
Примеры первообразныхf x 2x,
X , .
2
F x x ,
2
G x x 6.
2. f x cos x
X ,
F x sin x
G x sin x 5
1.
12.
Утверждения:промежутке X
- первообразная f
1. Пусть на
F x
x .
13.
Утверждения:промежутке X
- первообразная f
1. Пусть на
F x
Тогда функция
x .
G x F x C ,
C - произвольная константа,
тоже первообразная f x .
где
14.
Утверждения:промежутке X
- первообразная f
1. Пусть на
F x
Тогда функция
x .
G x F x C ,
C - произвольная константа,
тоже первообразная f x .
где
.
Док-во:
G x F x C F x f x .
15.
2. ЕслиF x и G x
первообразные одной функции
то
G x F x C.
f x ,
16.
2. ЕслиF x и G x
первообразные одной функции
то
f x ,
G x F x C.
Док-во:
(G x F x ) G x F x 0.
17.
2. ЕслиF x и G x
первообразные одной функции
то
f x ,
G x F x C.
Док-во:
(G x F x ) G x F x 0.
Производная разности функций равна 0 –
разность функций равна const.
Вывод: общий вид всех первообразных
F x C.
18.
Неопределенный интегралМножество всех первообразных для функции f
на промежутке
x
X называется неопределенным
интегралом и обозначается
.
19.
Неопределенный интегралМножество всех первообразных для функции f
на промежутке
x
X называется неопределенным
интегралом и обозначается
f x dx F x C
.
20.
Неопределенный интегралМножество всех первообразных для функции f
на промежутке
X называется неопределенным
интегралом и обозначается
f x dx F x C
f x
- подынтегральная функция, а
f x dx
x
.
- подынтегральное выражение
21.
Слайд № 21Пример
f x x
22.
Слайд № 22Пример
f x x
2
x
- первообразная, ( F x x );
F x
2
2
x
xdx C - неопределенный интеграл
2
23.
Стандартные интегралы1 dx x C
x 1
;
24.
Стандартные интегралыx 1
1 dx x C
a
x dx
a
1
x
a 1
C
a 1
;
25.
Стандартные интегралыx 1
1 dx x C
a
x dx
a
1
x
a 1
C
a 1
x a 1 a 1 x a 1 1
a
x
a 1
a
1
;
26.
1x dx ln | x | C
27.
1x dx ln | x | C
1
ln x ,
x
1
ln ( x)
x
28.
1x dx ln | x | C
1
ln x ,
x
1
ln | x |
x
1
ln ( x)
x
29.
1x dx ln | x | C
1
ln x ,
x
x
x
e dx e C
1
ln | x |
x
1
ln ( x)
x
e
x
x
e
30.
1x dx ln | x | C
1
ln x ,
x
1
ln ( x)
x
x
x
e dx e C
x
a dx
1
ln | x |
x
x
a
ln a
C
e
x
x
e
ax
ax
ln a
31.
cos xdx sin x Csin x cos x
sin
xdx
cos
x
C
cos x sin x
,
32.
cos xdx sin x Csin x cos x
sin
xdx
cos
x
C
cos x sin x
1
2
cos x
,
dx tg x C
tg x
1
2
cos x
33.
cos xdx sin x Csin x cos x
sin
xdx
cos
x
C
cos x sin x
dx tg x C
tg x
dx ctg x C
ctg x
1
2
cos x
1
2
sin x
,
1
2
cos x
1
2
sin x
34.
.1
2
1 x
dx arctg x C
arctg x
1
2
1 x
35.
12
1 x
dx arctg x C
1
2
1 x
arctg x
1
2
1 x
dx arcsin x C
arcsin x
.
1
2
1 x
36.
Свойства интеграловИз определения неопределенного интеграла
f x dx F x C
F x f x
37.
Свойства интеграловИз определения неопределенного интеграла
F x f x
f x dx F x C
f x dx f x
Следует
38.
Свойства интеграловИз определения неопределенного интеграла
F x f x
f x dx F x C
f x dx f x
Следует
1.
d f x dx f x dx
39.
Свойства интеграловИз определения неопределенного интеграла
F x f x
f x dx F x C
f x dx f x
Следует
1.
d f x dx f x dx
Т.к. d f x dx f x dx dx f x dx
40.
Свойства интеграловИз определения неопределенного интеграла
F x f x
f x dx F x C
f x dx f x
Следует
1.
d f x dx f x dx
Т.к. d f x dx f x dx dx f x dx
2. dF x F x C
41.
Свойства интеграловИз определения неопределенного интеграла
F x f x
f x dx F x C
f x dx f x
Следует
1.
d f x dx f x dx
Т.к. d f x dx f x dx dx f x dx
2. dF x F x C
3. af x dx a f x dx
42.
Свойства интеграловИз определения неопределенного интеграла
F x f x
f x dx F x C
f x dx f x
Следует
1.
d f x dx f x dx
Т.к. d f x dx f x dx dx f x dx
2. dF x F x C
3. af x dx a f x dx
4. f x g x dx f x dx g x dx
43.
Пример 1.
2
x
( x 3 cos x 4e )dx
44.
Пример 1.
2
x
( x 3 cos x 4e )dx
2
x
x dx 3 cos xdx 4 e dx
45.
Пример 1.
2
x
( x 3 cos x 4e )dx
2
x
x dx 3 cos xdx 4 e dx
3
x
3
x
3 sin x 4e C
46.
.Пример 2
4
x 5x 4
dx
2
x
47.
.Пример 2
4
5 4
x 5x 4
2
(
x
)
dx
dx
2
2
x
x
x
48.
.Пример 2
4
5 4
x 5x 4
2
(
x
)
dx
dx
2
2
x
x
x
x3
5ln x ( 4 x 2 )dx
3
49.
.Пример 2
4
5 4
x 5x 4
2
(
x
)
dx
dx
2
2
x
x
x
x3
5ln x ( 4 x 2 )dx
3
x3
4 3
5ln x x C
3
3
50.
Пример 3x2
2 dx
x 1
51.
Пример 32 1 1
x2
x
dx
2 dx 2
x 1
x 1
52.
Пример 32 1 1
x2
x
dx
2 dx 2
x 1
x 1
1
(1 2 )dx
x 1
53.
Пример 32 1 1
x2
x
dx
2 dx 2
x 1
x 1
1
(1 2 )dx x arctgx C
x 1
54.
Метод замены переменной.Введение под знак дифференциала
Утверждение:
если известно
f t dt F (t ) C
55.
Метод замены переменной.Введение под знак дифференциала
Утверждение:
если известно
f t dt F (t ) C
( F (t ) f (t ) )
56.
Метод замены переменной.Введение под знак дифференциала
Утверждение:
если известно
f t dt F (t ) C
( F (t ) f (t ) )
то тогда
f x x dx F ( ( x)) C
57.
Метод замены переменной.Введение под знак дифференциала
Утверждение:
если известно
f t dt F (t ) C
( F (t ) f (t ) )
то тогда
f x x dx F ( ( x)) C
Функции
f (t ), ( x), ( x)
предполагаются непрерывными.
58.
F (t ) f (t )Док-во:
По правилу дифференцирования сложной функции
F ( ( x)) F ( ( x)) ( x)
59.
F (t ) f (t )Док-во:
По правилу дифференцирования сложной функции
F ( ( x)) F ( ( x)) ( x)
f ( ( x)) ( x)
60.
F (t ) f (t )Док-во:
По правилу дифференцирования сложной функции
F ( ( x)) F ( ( x)) ( x)
f ( ( x)) ( x)
Т.е.
f x x dx F ( ( x))dx F ( ( x)) C
61.
Почему замена переменной?Можно вводить (заменять) новую переменную
62.
Почему замена переменной?Можно вводить (заменять) новую переменную
f x x dx
63.
Почему замена переменной?Можно вводить (заменять) новую переменную
f x x dx
{ t x , dt x dx }
64.
Почему замена переменной?Можно вводить (заменять) новую переменную
f x x dx
{ t x , dt x dx }
f t dt F (t ) C F ( ( x)) C
65.
Пример:3
sin x cos x dx
,
66.
Пример:3
sin x cos x dx
t sin x , dt t ( x) dx ,
67.
Пример:3
sin x cos x dx
t sin x , dt t ( x) dx , dt cos x dx
68.
Пример:3
sin x cos x dx
t sin x , dt t ( x) dx , dt cos x dx
3
t dt
69.
Пример:3
sin x cos x dx
t sin x , dt t ( x) dx , dt cos x dx
3
t dt
4
t
4
C
4
sin x
4
C
70.
Введение под знак дифференциалаf x x dx f x d x
F ( ( x)) C
71.
Введение под знак дифференциалаf x x dx f x d x
F ( ( x)) C
Пример
3
sin x cos x dx
72.
Введение под знак дифференциалаf x x dx f x d x
F ( ( x)) C
Пример
3
sin x cos x dx
{ cos x dx d sin x }
73.
Введение под знак дифференциалаf x x dx f x d x
F ( ( x)) C
Пример
3
sin x cos x dx
3
sin x d sin x
{ cos x dx d sin x }
74.
Введение под знак дифференциалаf x x dx f x d x
F ( ( x)) C
Пример
3
sin x cos x dx
{ cos x dx d sin x }
4
sin x
3
sin x d sin x
C
4
75.
Примеры,
,
10
( x 10) dx
76.
Примеры,
,
10
( x 10) dx
t x 10
dt t dx, dt dx
77.
Примеры,
10
( x 10) dx
,
10
t dt
11
t
11
t x 10
dt t dx, dt dx
C
78.
Примеры,
10
( x 10) dx
,
10
t dt
11
t
11
t x 10
dt t dx, dt dx
C
11
( x 10)
11
C
79.
Примеры,
10
( x 10) dx
,
10
t dt
11
t
11
t x 10
dt t dx, dt dx
C
11
( x 10)
11
C
10
10
( x 10) dx ( x 10) d ( x 10)
80.
Примеры,
10
( x 10) dx
,
10
t dt
11
t
11
t x 10
dt t dx, dt dx
C
11
( x 10)
11
C
10
10
( x 10) dx ( x 10) d ( x 10)
11
( x 10)
11
C
81.
Пример:cos( 2 x)dx
82.
Пример:cos( 2 x)dx t 2 x
83.
Пример:cos( 2 x)dx t 2 x
dt t ( x) dx,
84.
Пример:cos( 2 x)dx t 2 x
dt
dt 2dx, dx
2
dt t ( x) dx,
85.
Пример:cos( 2 x)dx t 2 x
dt t ( x) dx,
1
1
dt
cos t dt sin t C
dt 2dx, dx
2
2
2
86.
Пример:cos( 2 x)dx t 2 x
dt t ( x) dx,
1
1
dt
cos t dt sin t C
dt 2dx, dx
2
2
2
1
sin( 2 x) C
2
87.
Пример:cos( 2 x)dx t 2 x
dt t ( x) dx,
1
1
dt
cos t dt sin t C
dt 2dx, dx
2
2
2
1
sin( 2 x) C
2
cos( 2 x)dx
88.
Пример:cos( 2 x)dx t 2 x
dt t ( x) dx,
1
1
dt
cos t dt sin t C
dt 2dx, dx
2
2
2
1
sin( 2 x) C
2
2
1
cos( 2 x)dx 2 cos 2 xdx 2 cos 2 xd (2 x)
89.
Пример:cos( 2 x)dx t 2 x
dt t ( x) dx,
1
1
dt
cos t dt sin t C
dt 2dx, dx
2
2
2
1
sin( 2 x) C
2
2
1
cos( 2 x)dx 2 cos 2 xdx 2 cos 2 xd (2 x)
1
sin( 2 x) C
2
90.
Пример:cos(2 x 3)dx
91.
Пример:cos(2 x 3)dx t 2 x 3 dt t ( x) dx,
92.
Пример:cos(2 x 3)dx t 2 x 3 dt t ( x) dx,
dt
dt 2dx, dx
2
93.
Пример:cos(2 x 3)dx t 2 x 3 dt t ( x) dx,
dt
1
1
dt 2dx, dx
cos t dt sin t C
2
2
2
94.
Пример:cos(2 x 3)dx t 2 x 3 dt t ( x) dx,
dt
1
1
dt 2dx, dx
cos t dt sin t C
2
2
2
1
sin(2 x 3) C
2
95.
Замена переменной. Примерыdx
f ln x x f t dt
1
t ln x, dt t dx dt dx
x
96.
Замена переменной. Примерыdx
f ln x x f t dt
1
t ln x, dt t dx dt dx
x
ln
x
t
2
ln x
t
x dx dx dt tdt C
2
x
97.
Замена переменной. Примерыdx
f ln x x f t dt
1
t ln x, dt t dx dt dx
x
ln
x
t
2
ln x
t
x dx dx dt tdt C
2
x
2
ln x
C
2
98.
Замена переменной. Примерыx
f e dx
f t
t dt
99.
Замена переменной. Примерыx
f e dx
f t
t dt
dt
x
x
t e , dt t dx dt e dx, dx
t
100.
Замена переменной. Примерыx
f e dx
f t
t dt
dt
x
x
t e , dt t dx dt e dx, dx
t
x
e
1 e2 x
dx
101.
Замена переменной. Примерыx
f e dx
f t
t dt
dt
x
x
t e , dt t dx dt e dx, dx
t
t ex,
dx 2 x 2
e t
1 e2 x
x
e
dt e xdx,
102.
Замена переменной. Примерыx
f e dx
f t
t dt
dt
x
x
t e , dt t dx dt e dx, dx
t
t ex,
dx 2 x 2
e t
1 e2 x
dt
2
1 t
x
e
dt e xdx,
103.
Замена переменной. Примерыx
f e dx
f t
t dt
dt
x
x
t e , dt t dx dt e dx, dx
t
t e x , dt e xdx,
dx
2
x
2
2
x
e t
1 e
dt
arctg t C arctg e x C
2
1 t
x
e
104.
Стандартные интегралыdx
1
dx
2 2 2 x 2
x a
a 1
a
105.
Стандартные интегралыx
d
dx
1
dx
1
1 dt
a
2 2
2
2 x 2
2
x a
a 1 a x 1 a t 1
a
a
106.
Стандартные интегралыx
d
dx
1
dx
1
1 dt
a
2 2
2
2 x 2
2
x a
a 1 a x 1 a t 1
a
a
1
1
arctg t C arctg ax C
a
a
107.
Стандартные интегралыx
d
dx
1
dx
1
1 dt
a
2 2
2
2 x 2
2
x a
a 1 a x 1 a t 1
a
a
1
1
arctg t C arctg ax C
a
a
dx
1
dx
2 2
a 1 x 2
a x
a
108.
Стандартные интегралыx
d
dx
1
dx
1
1 dt
a
2 2
2
2 x 2
2
x a
a 1 a x 1 a t 1
a
a
1
1
arctg t C arctg ax C
a
a
x
d
dx
1
dx
a
2 2
2
a 1 x 2
a x
x
1 a
a
109.
Стандартные интегралыx
d
dx
1
dx
1
1 dt
a
2 2
2
2 x 2
2
x a
a 1 a x 1 a t 1
a
a
1
1
arctg t C arctg ax C
a
a
x
d
dx
1
dx
a
2 2
2
a 1 x 2
a x
x
1 a
a
dt
1 t
2
arcsin t C arcsin ax C
110.
Интегрирование по частямПусть функции u (x) и v (x )
дифференцируемые и u ( x )v ( x )
имеет первообразную, тогда u ( x )v ( x )
тоже имеет первообразную, причем
uv dx uv u vdx
(x ) опускаем
111.
Док-во.uv u v uv uv uv u v
112.
Док-во.uv u v uv uv uv u v
Из последнего равенства следует
uv dx uv dx u vdx
113.
Док-во.uv u v uv uv uv u v
Из последнего равенства следует
uv dx uv dx u vdx
По определению
uv dx uv C
114.
Док-во.uv u v uv uv uv u v
Из последнего равенства следует
uv dx uv dx u vdx
По определению
uv dx uv C
Следовательно
uv dx uv u vdx
ч.т.д.
115.
uv dx uv u vdxТак как
,
v dx dv u dx du
116.
uv dx uv u vdxТак как
,
v dx dv u dx du
udv uv vdu
117.
uv dx uv u vdxТак как
,
v dx dv u dx du
udv uv vdu
du u dx, v dv
118.
udv uv vduИнтегралы
вида
Pn ( x) f ( x)dx
119.
udv uv vduИнтегралы
вида
Pn ( x) f ( x)dx
kx ,
1 Pn x - многочлен, а f x e
120.
udv uv vduИнтегралы
вида
Pn ( x) f ( x)dx
kx ,
1 Pn x - многочлен, а f x e
f x coskx , или f x sin kx , тогда
121.
udv uv vduИнтегралы
вида
Pn ( x) f ( x)dx
kx ,
1 Pn x - многочлен, а f x e
f x coskx , или f x sin kx , тогда
u Pn x , а dv f x dx
122.
udv uv vduИнтегралы
вида
Pn ( x) f ( x)dx
kx ,
1 Pn x - многочлен, а f x e
f x coskx , или f x sin kx , тогда
u Pn x , а dv f x dx
123.
udv uv vduИнтегралы
вида
Pn ( x) f ( x)dx
kx ,
1 Pn x - многочлен, а f x e
f x coskx , или f x sin kx , тогда
u Pn x , а dv f x dx
Пример.
u x
x cos 2 x dx dv cos 2 x dx
124.
udv uv vduИнтегралы
вида
Pn ( x) f ( x)dx
kx ,
1 Pn x - многочлен, а f x e
f x coskx , или f x sin kx , тогда
u Pn x , а dv f x dx
Пример.
u x
du dx
x cos 2 x dx dv cos 2 x dx v 1 sin 2 x
2
125.
udv uv vduПример.
u x
du dx
x cos 2 x dx dv cos 2 x dx v 1 sin 2 x
2
126.
udv uv vduПример.
u x
du dx
x cos 2 x dx dv cos 2 x dx v 1 sin 2 x
2
1
1
x sin 2 x sin 2 x dx
2
2
127.
udv uv vduПример.
u x
du dx
x cos 2 x dx dv cos 2 x dx v 1 sin 2 x
2
1
1
x sin 2 x sin 2 x dx
2
2
1
1 1
x sin 2 x ( cos 2 x) C
2
2 2
128.
udv uv vduПример.
u x
du dx
x cos 2 x dx dv cos 2 x dx v 1 sin 2 x
2
1
1
x sin 2 x sin 2 x dx
2
2
1
1 1
x sin 2 x ( cos 2 x) C
2
2 2
1
1
x sin 2 x cos 2 x C
2
4



























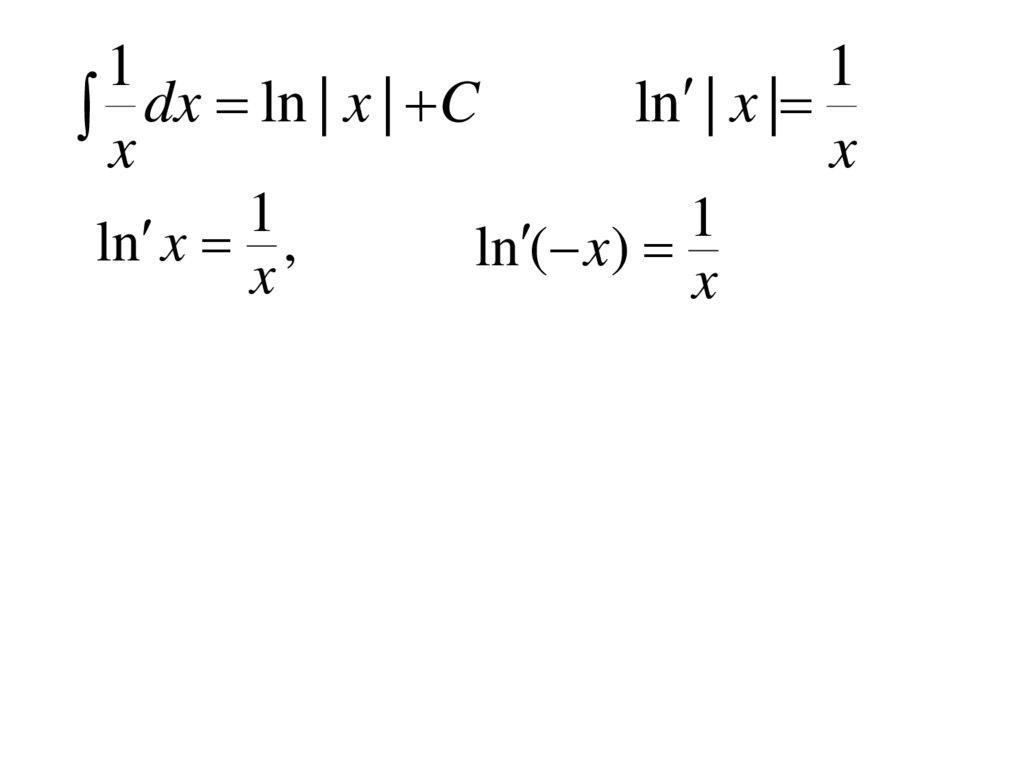
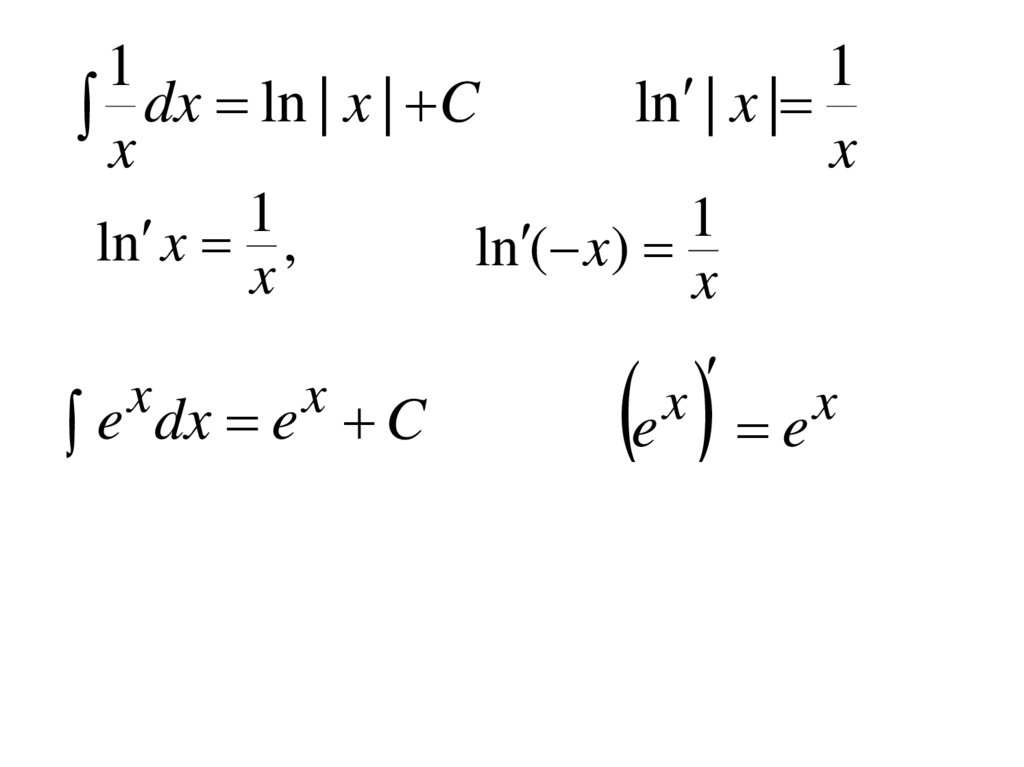


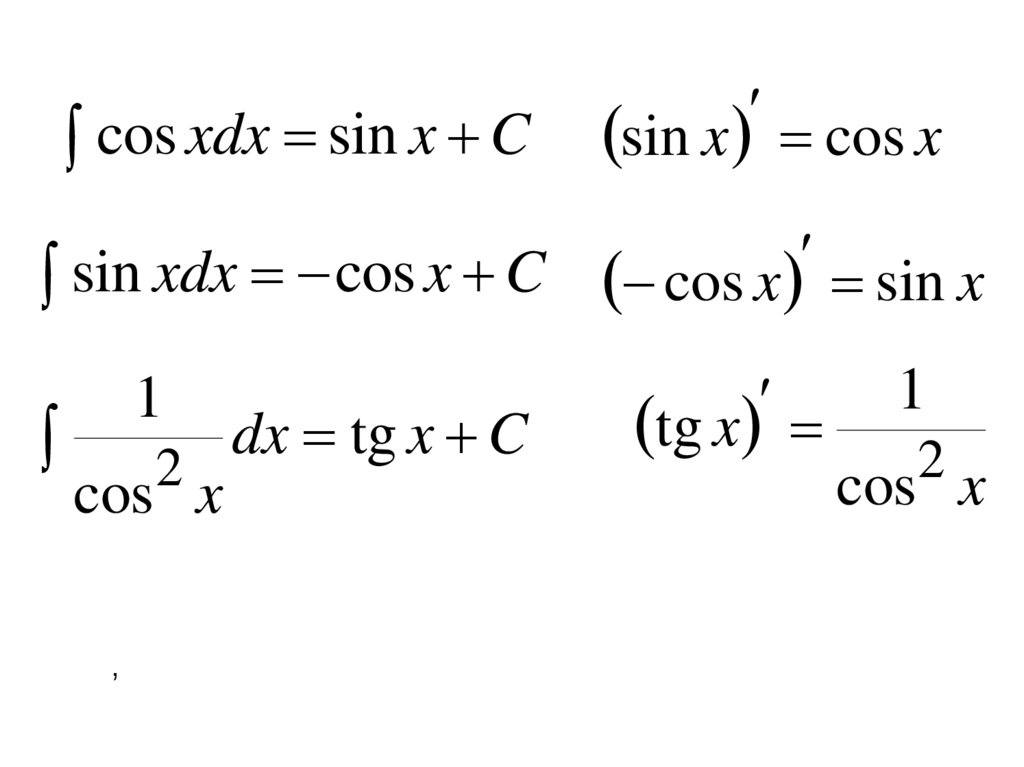
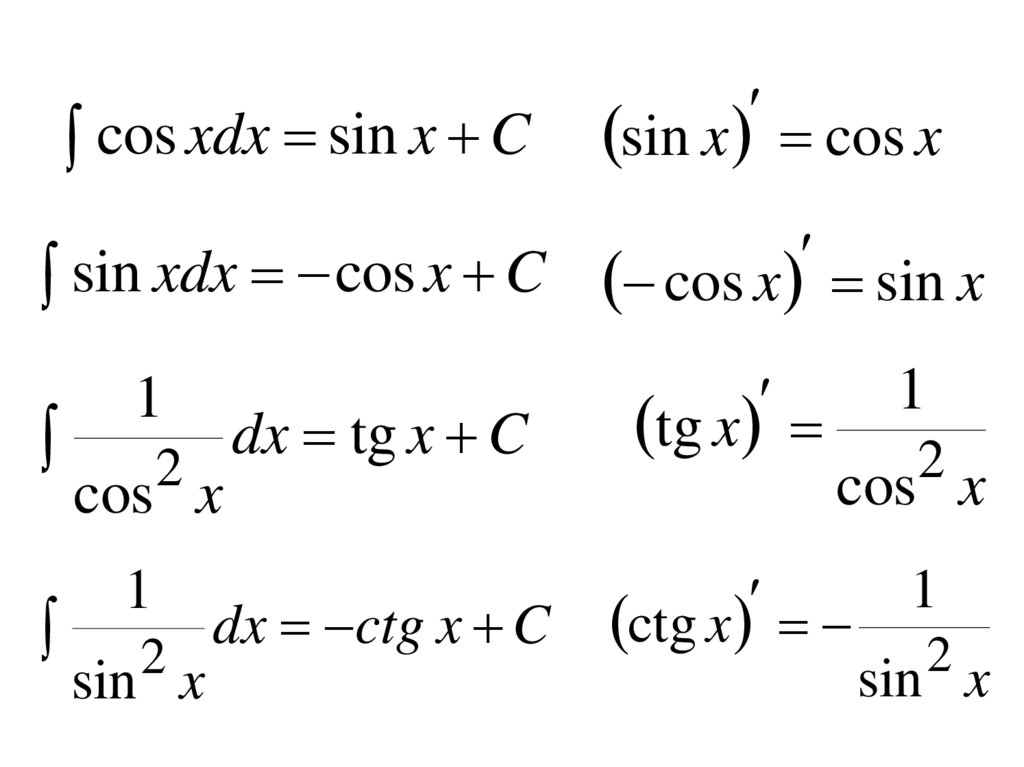
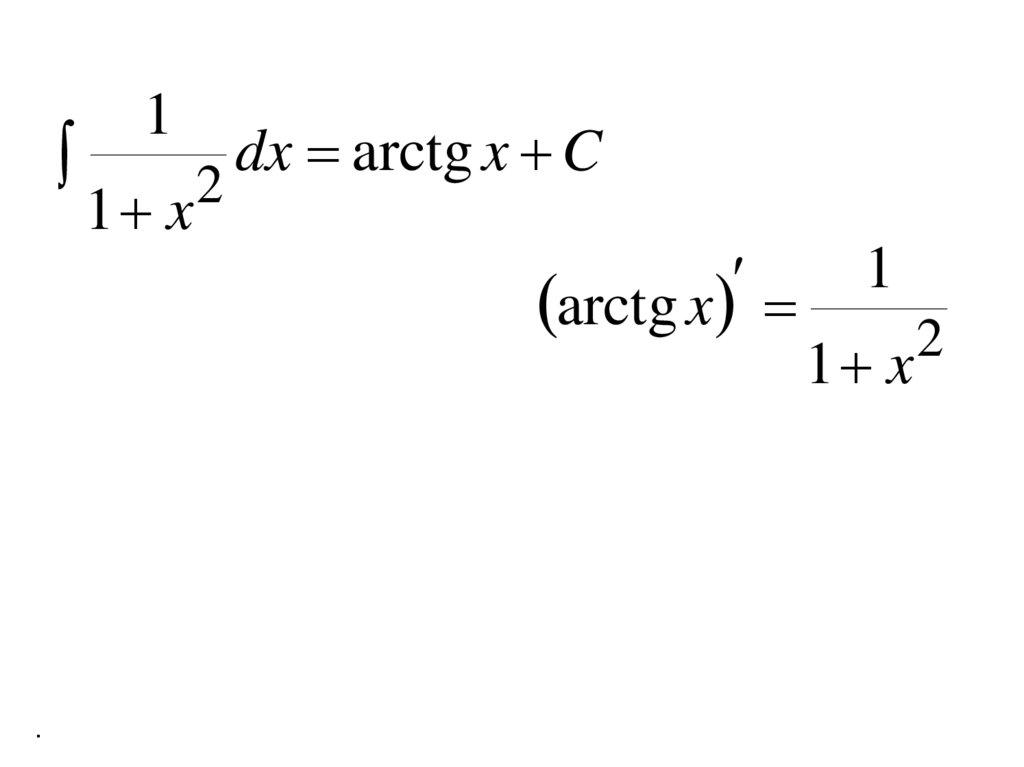
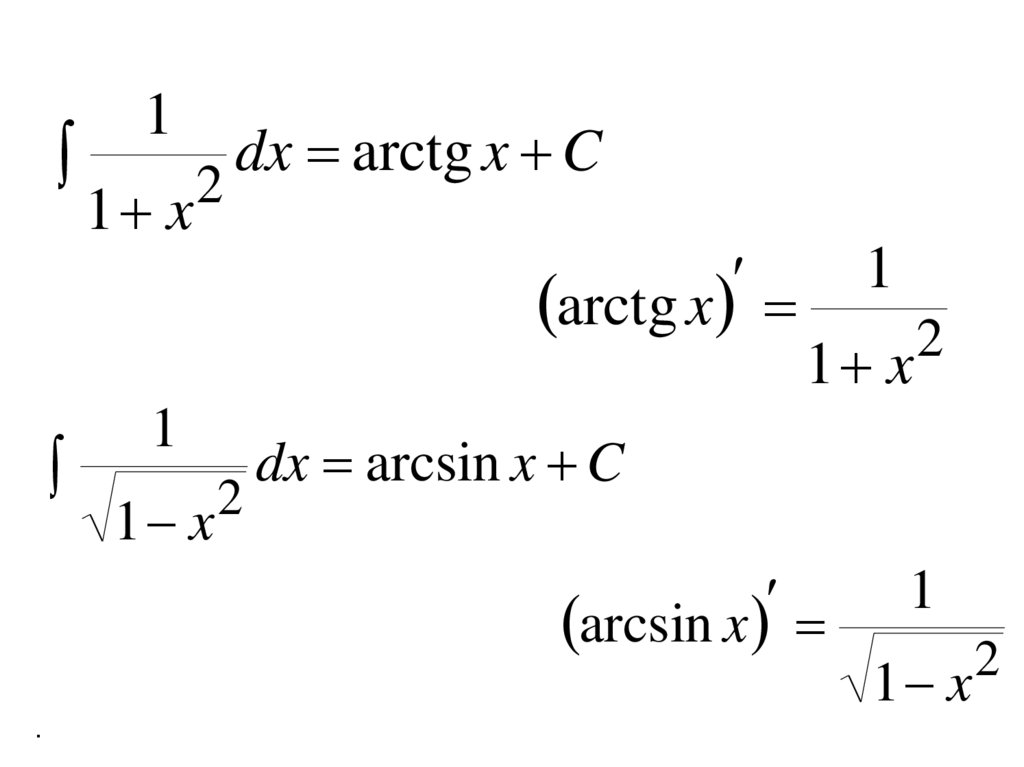







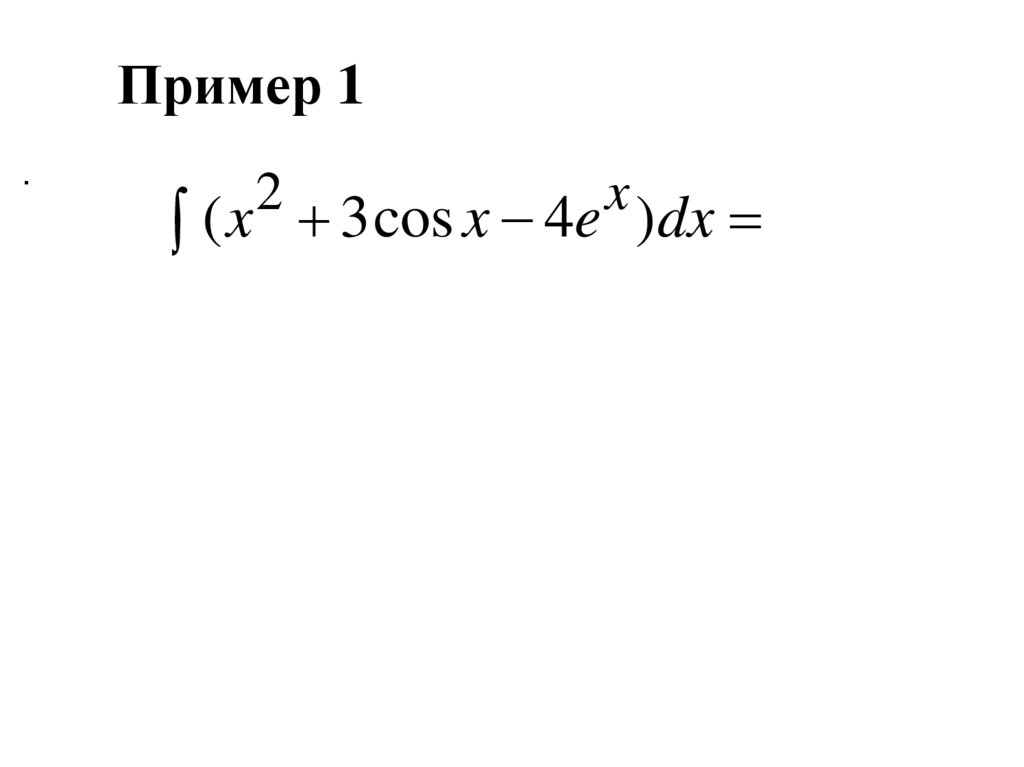
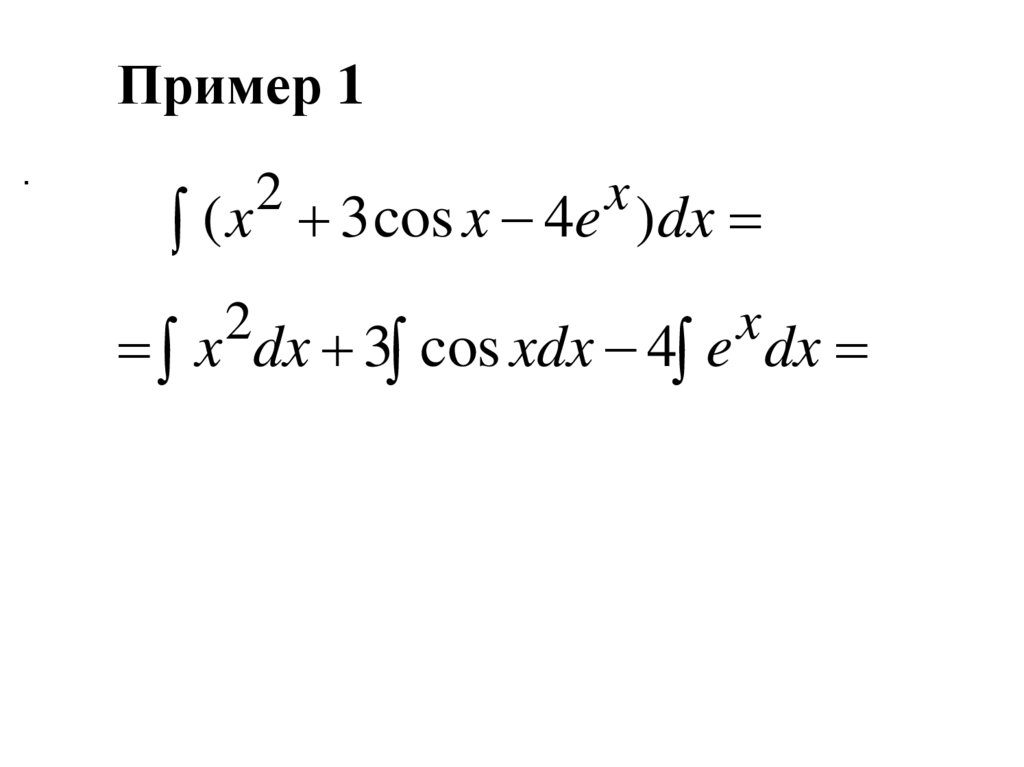


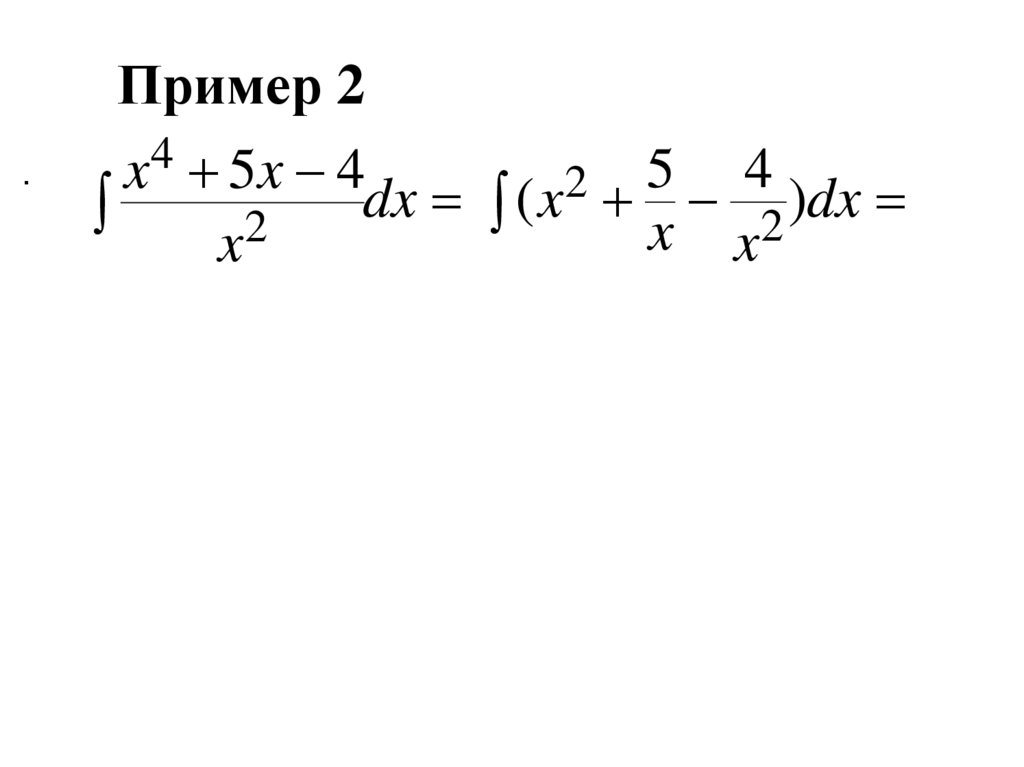
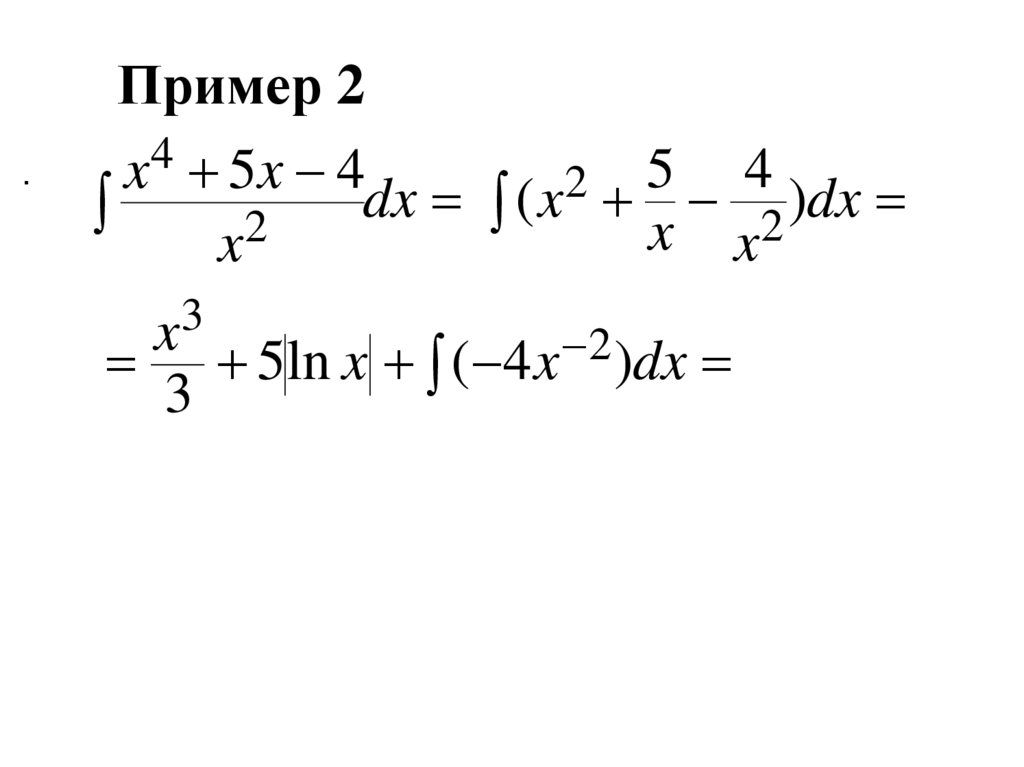
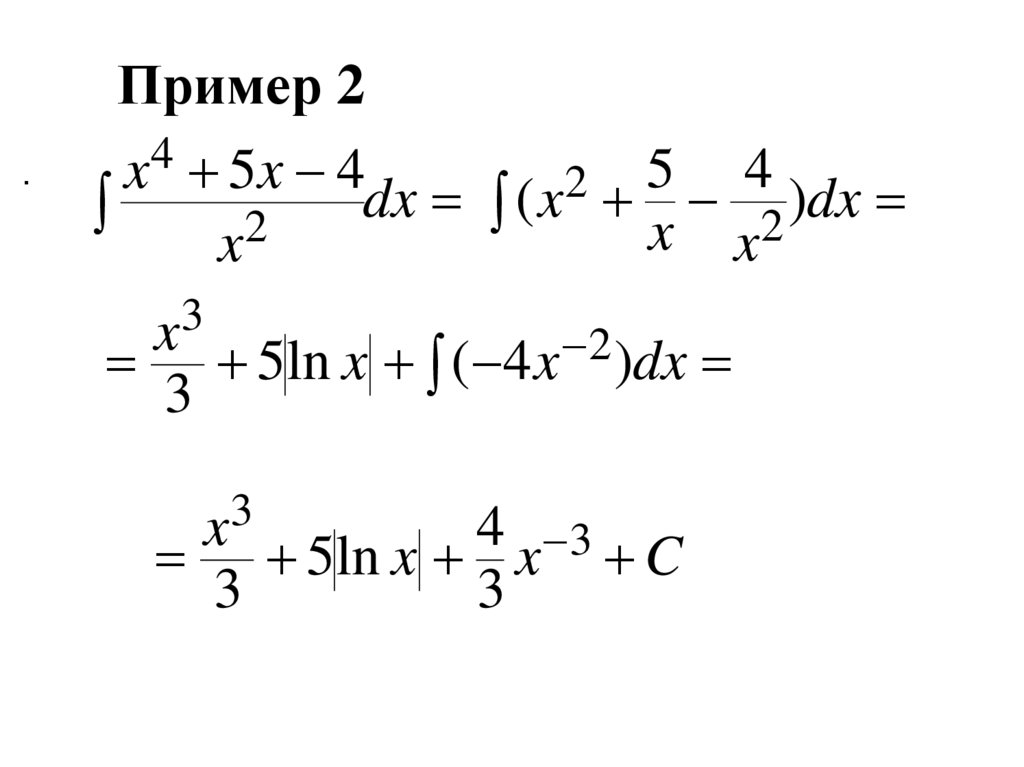
















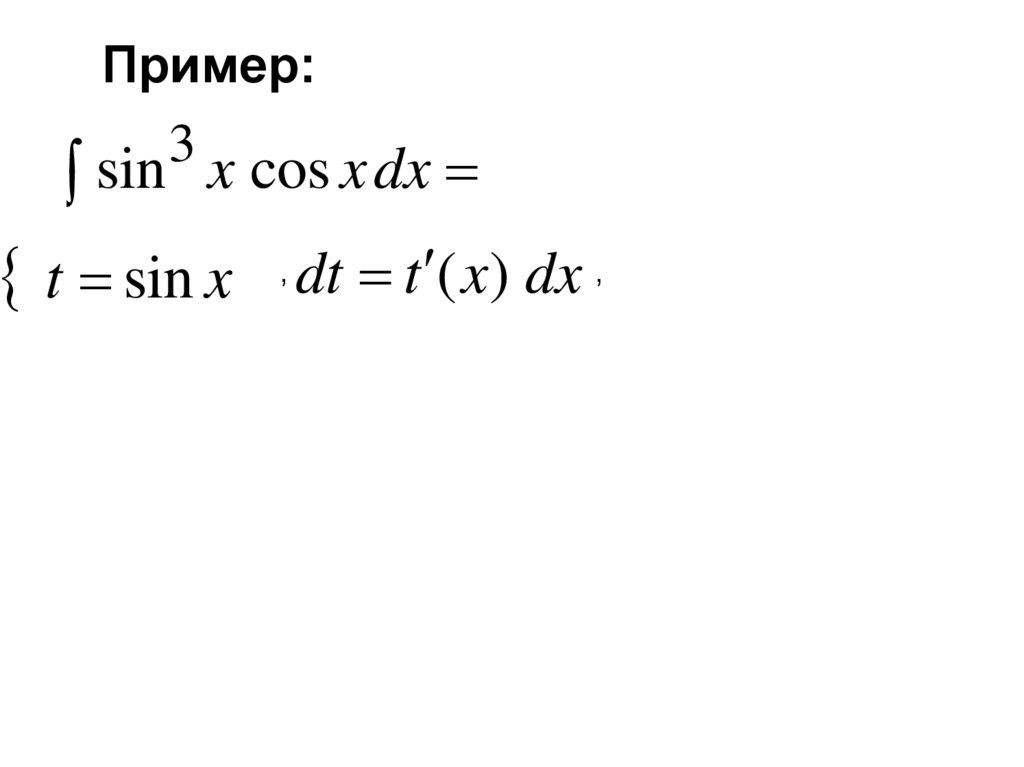
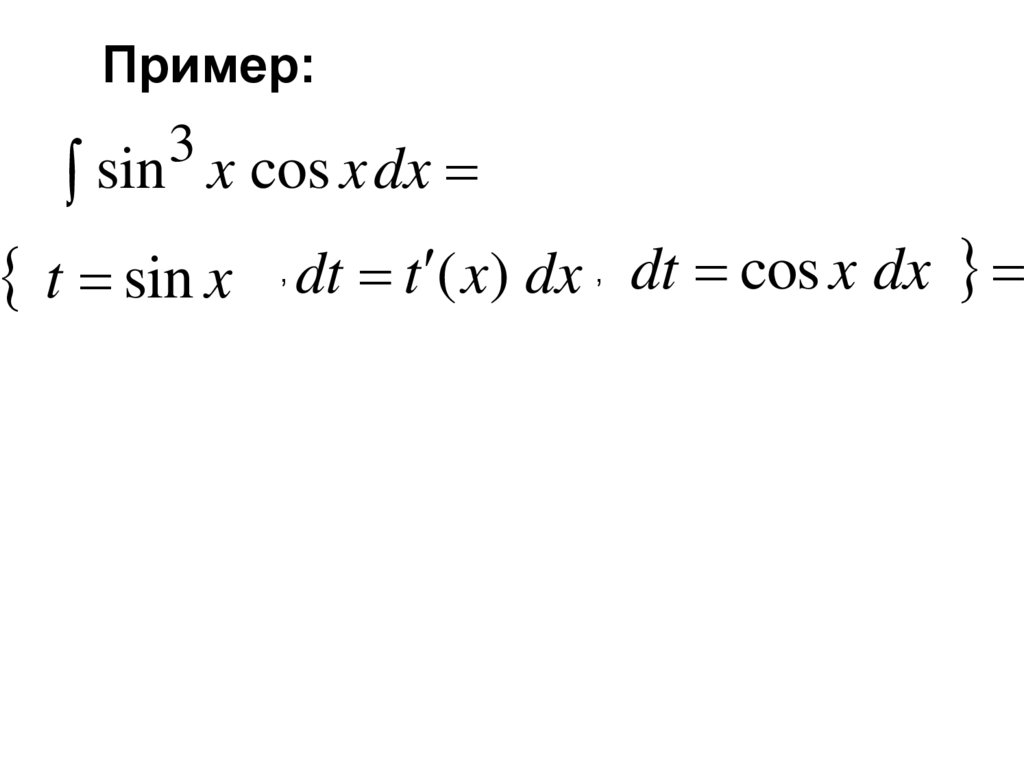
























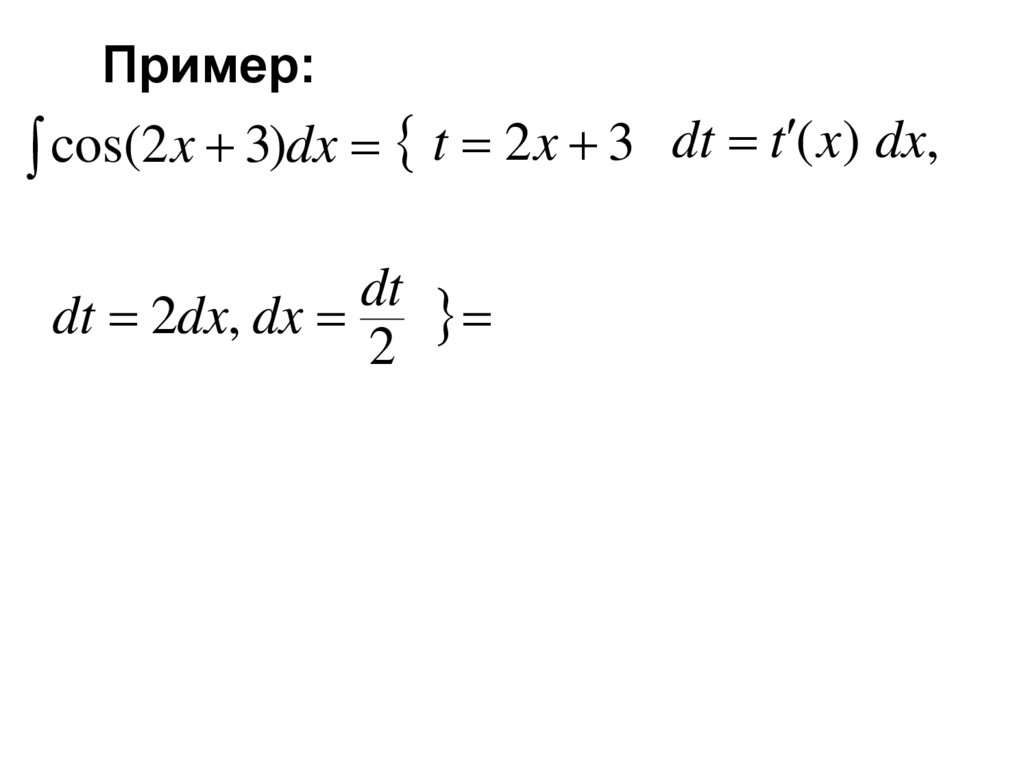

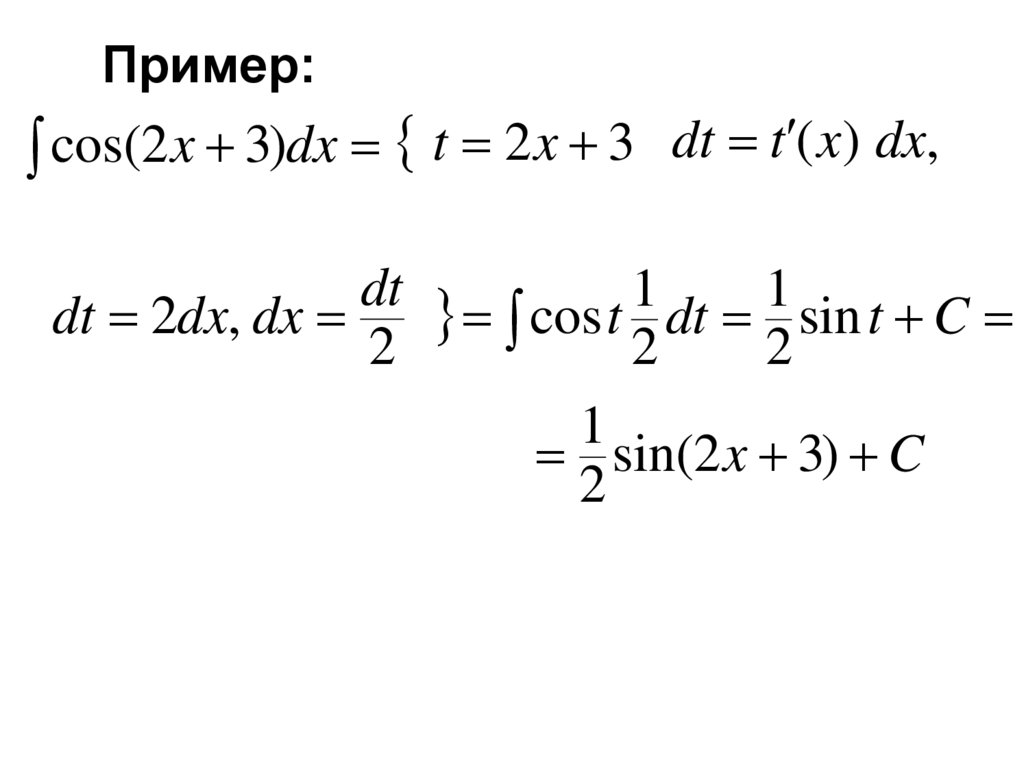
















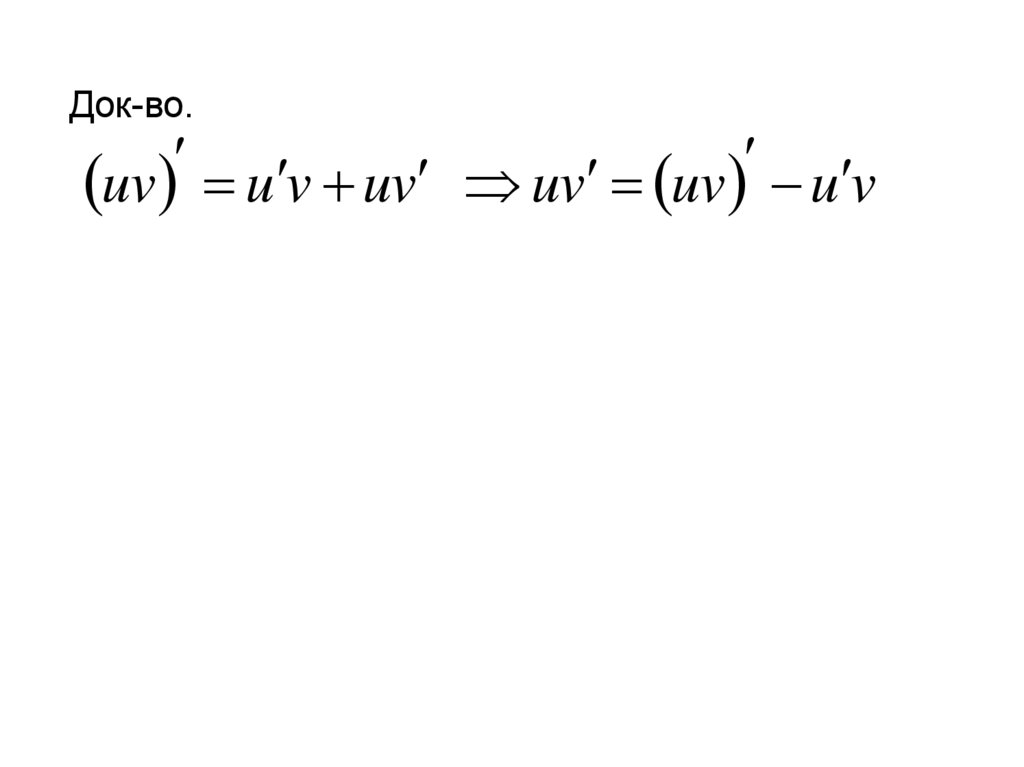



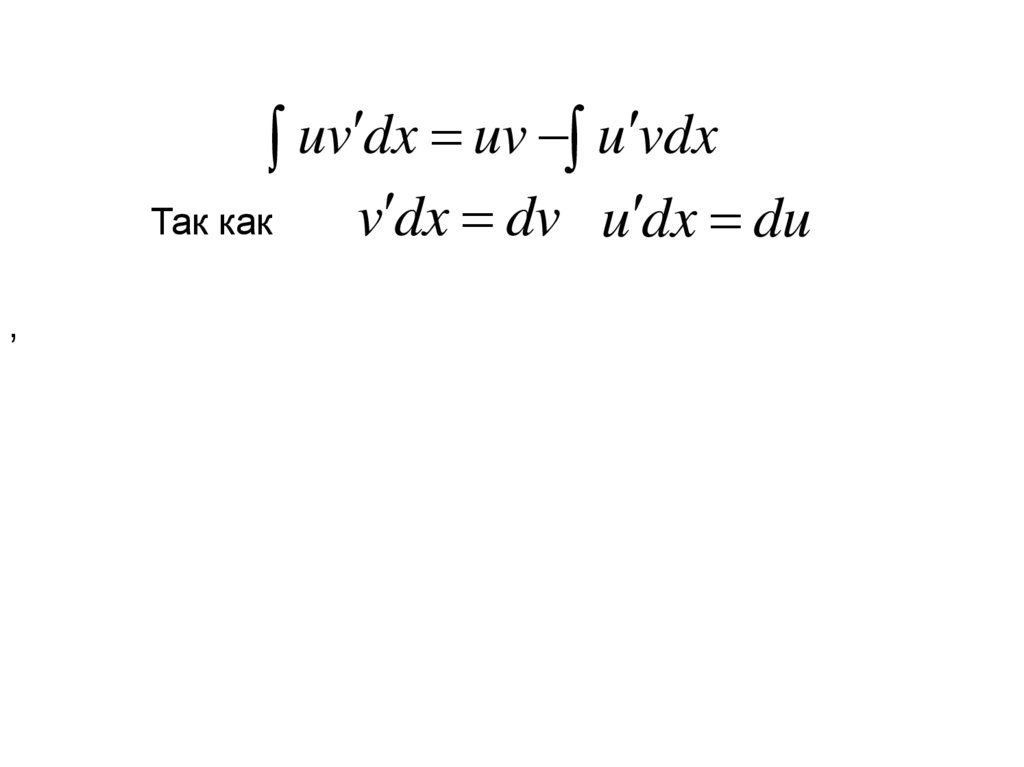



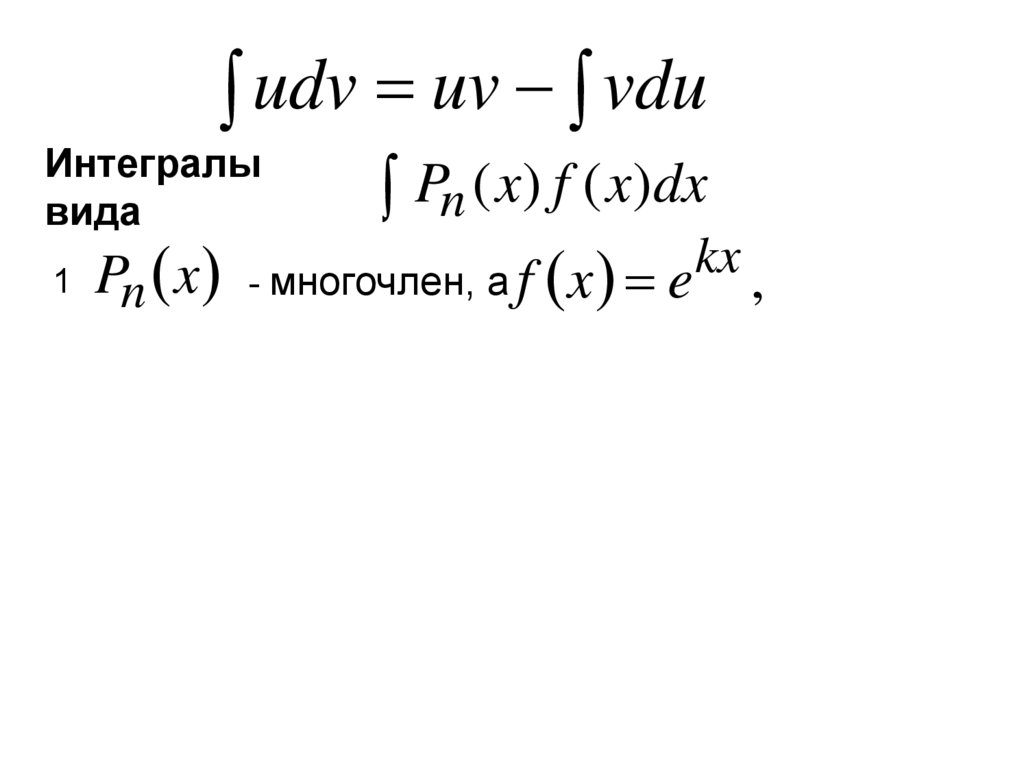
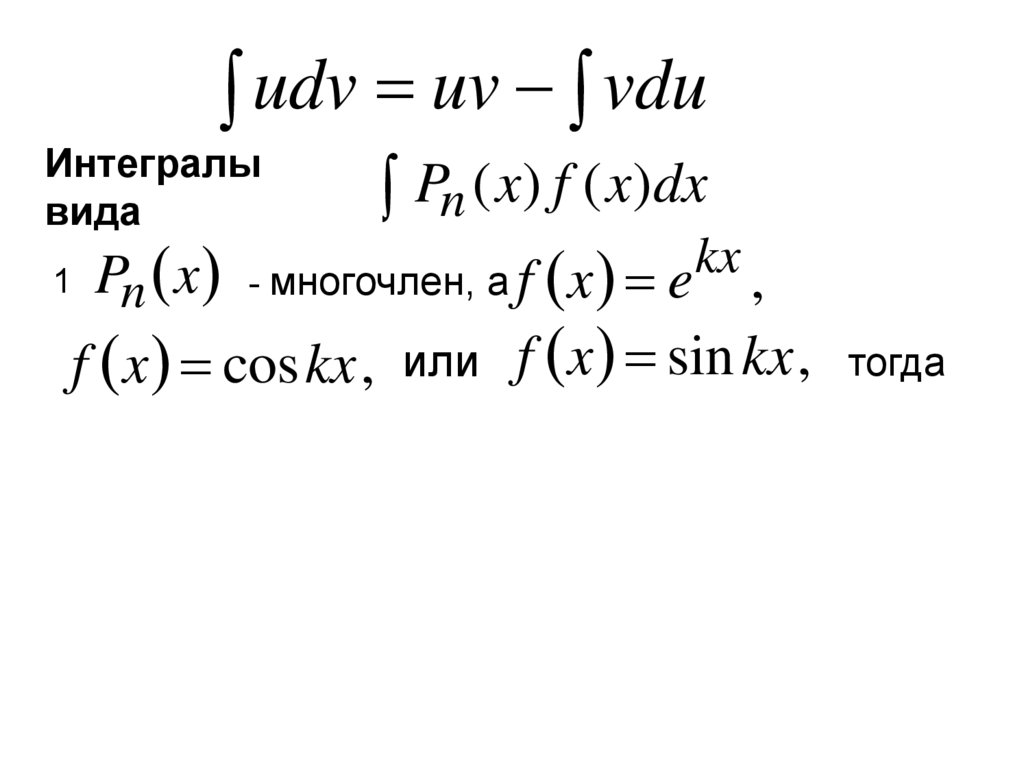


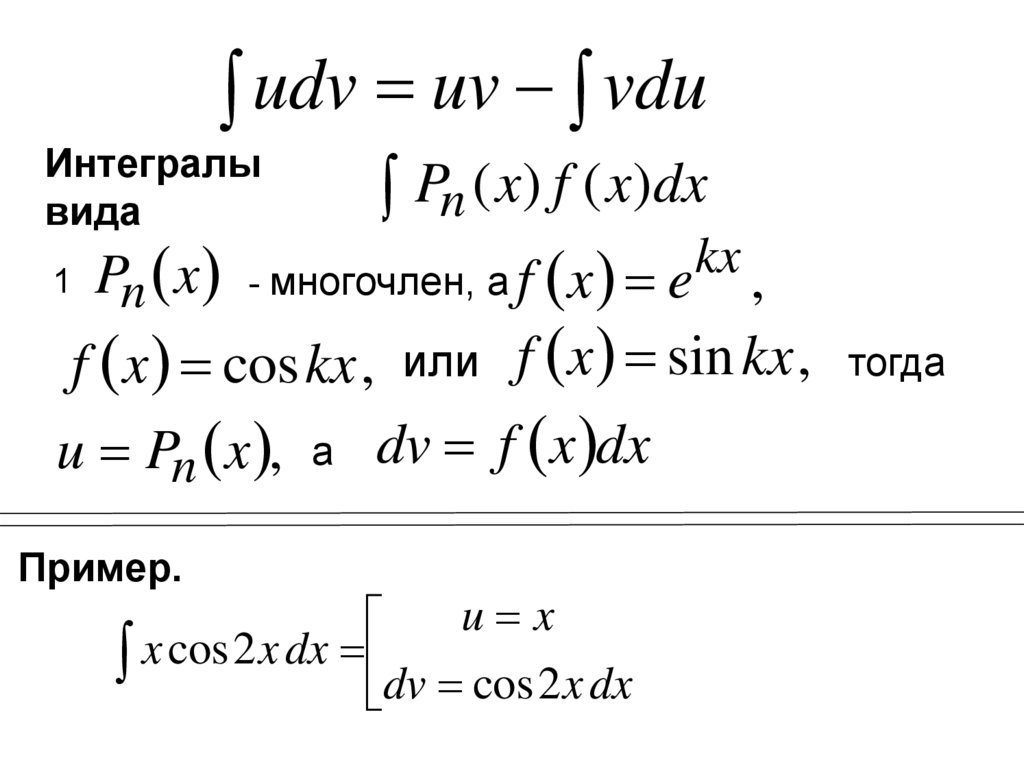
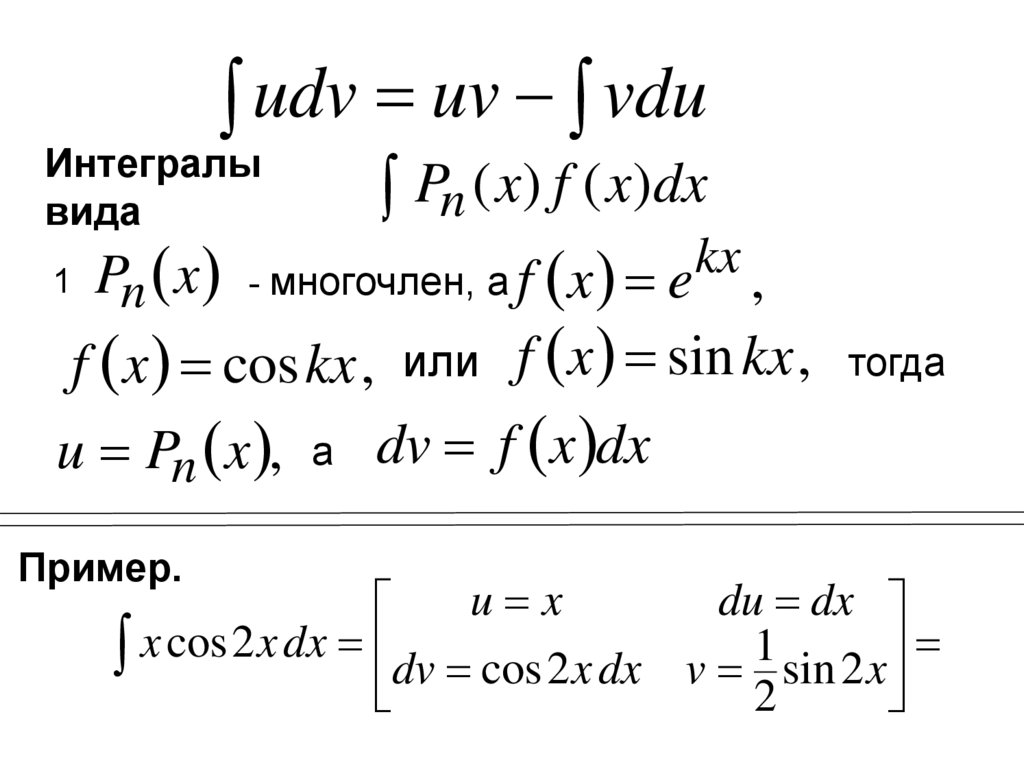

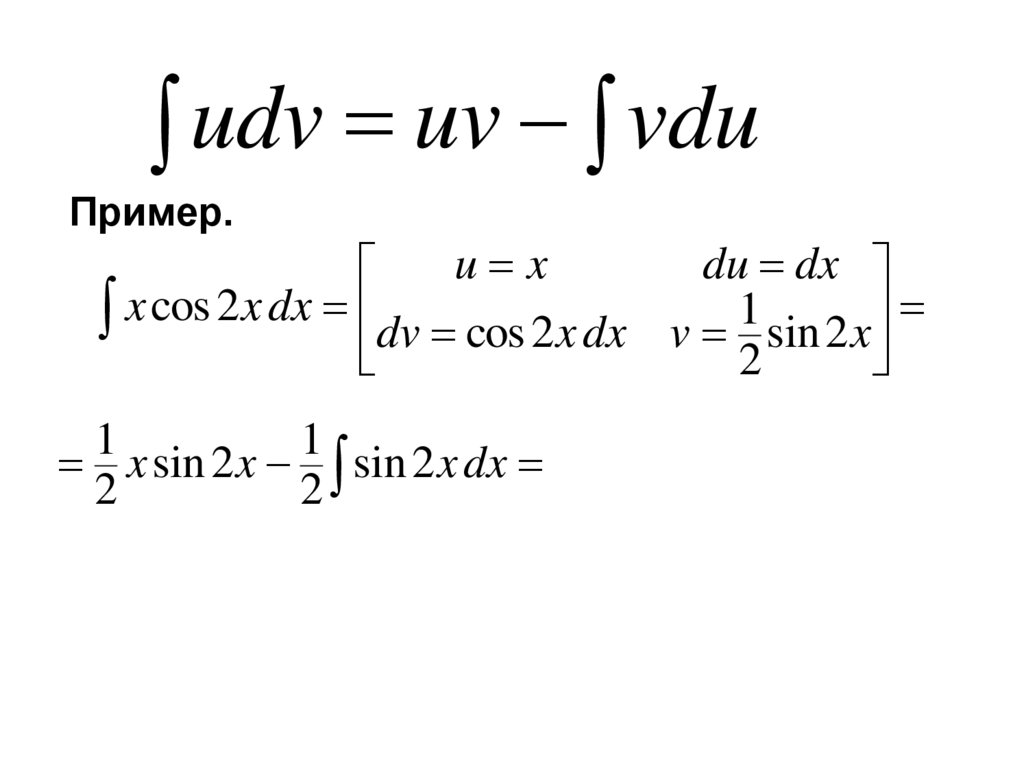
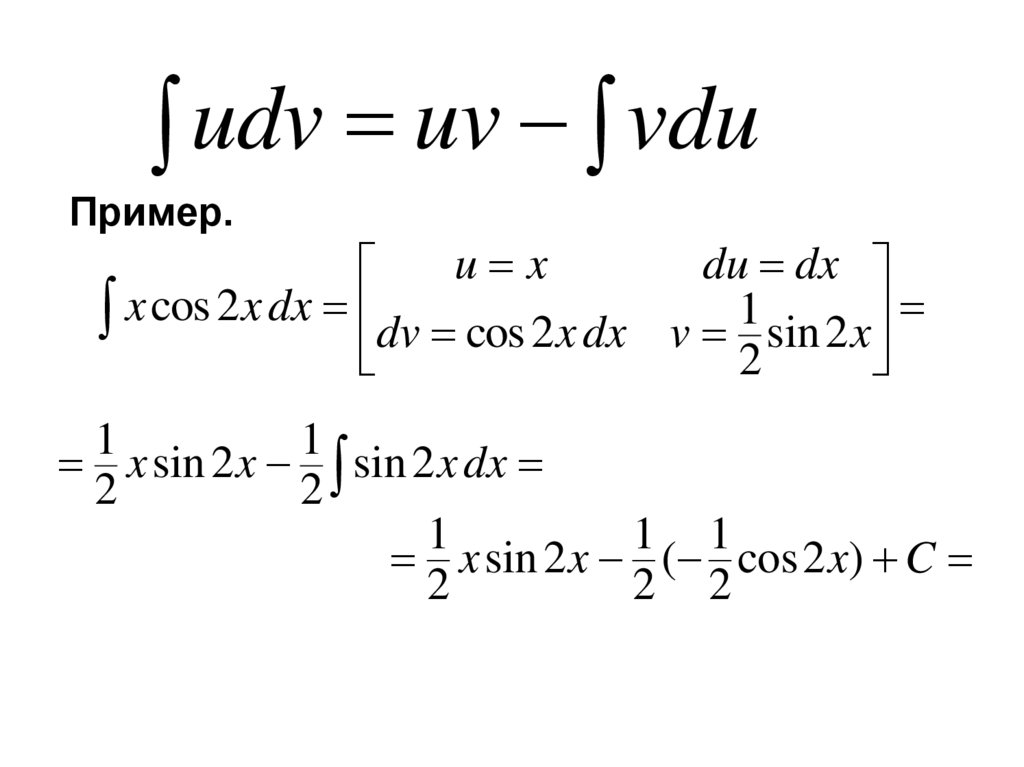

 mathematics
mathematics








