Механика и молекулярная физика. I семестр

1. Лекции по общему курсу физики. Механика и молекулярная физика I семестр

Псковский государственный университет
Лекции по общему
курсу физики.
Механика и
молекулярная физика
I семестр

2. Основная литература:

1)
2)
3)
4)
5)
Детлаф А. А. Курс физики: учебное пособие для втузов /
А. А. Детлаф, Б. М. Яворский. — 7-е изд., стер. —
Москва: Издательский центр Академия, 2008. - 720 с.
Савельев И. В. Курс общей физики. Т. 1. Механика.
Молекулярная физика: учебное пособие для втузов / И. В.
Савельев. — Изд. 9-е, стер. — Санкт-Петербург: Лань,
2007. — 432 с..
Иродов И. Е. Задачи по общей физике: учебное пособие /
И. Е. Иродов. — Изд. 9-е, стер. - Санкт-Петербург:
ЛАНЬ, 2005. - 416 с.
Волькенштейн В.С. Сборник задач по общему курсу
физики.- М.: Наука, 1985 (2008).
Александров Н.В., Яшкин А.Я. Курс общей физики. М.:
1978. – 416 с.

3. Курс общей физики

Основные разделы курса
Механика
Молекулярная физика и термодинамика
Электродинамика
Оптика
Атомная и ядерная физика
Квантовая физика
3

4. 1. Механика, ее разделы и абстракции, применяемые при изучении движений

Определения:
Механика - учение о простейшей форме движения
материи, которое состоит в перемещении тел или их
частей относительно друг друга. Механика - учение о
механическом движении.
Механика состоит из кинематики, статики и динамики.
Материальная точка – это тело, имеющее массу,
размерами которого можно пренебречь по сравнению с
размерами, характеризующими движение этого тела.
Совокупность нескольких тел, каждое из которых
можно считать материальной точкой, называется
системой материальных точек.
4

5.

Абсолютно твердое тело - система материальных
частиц, расстояние между которыми не изменяется при
произвольных перемещениях этой системы. Это тело,
которое ни при каких условиях не деформируется.
Механическое движение – это процесс изменения
положения тела или его частей по отношению к другим
телам или друг другу.
Произвольно выбранное неподвижное тело, по
отношению к которому рассматривается движение
данного тела, называется телом отсчета.
Система отсчета – это совокупность тела отсчета,
связанной с ним системы координат и механизма отсчета
времени (например, часов).
5

6. Три способа аналитического описания движения точки в пространстве

Естественный способ
Векторный способ
Координатный способ
6

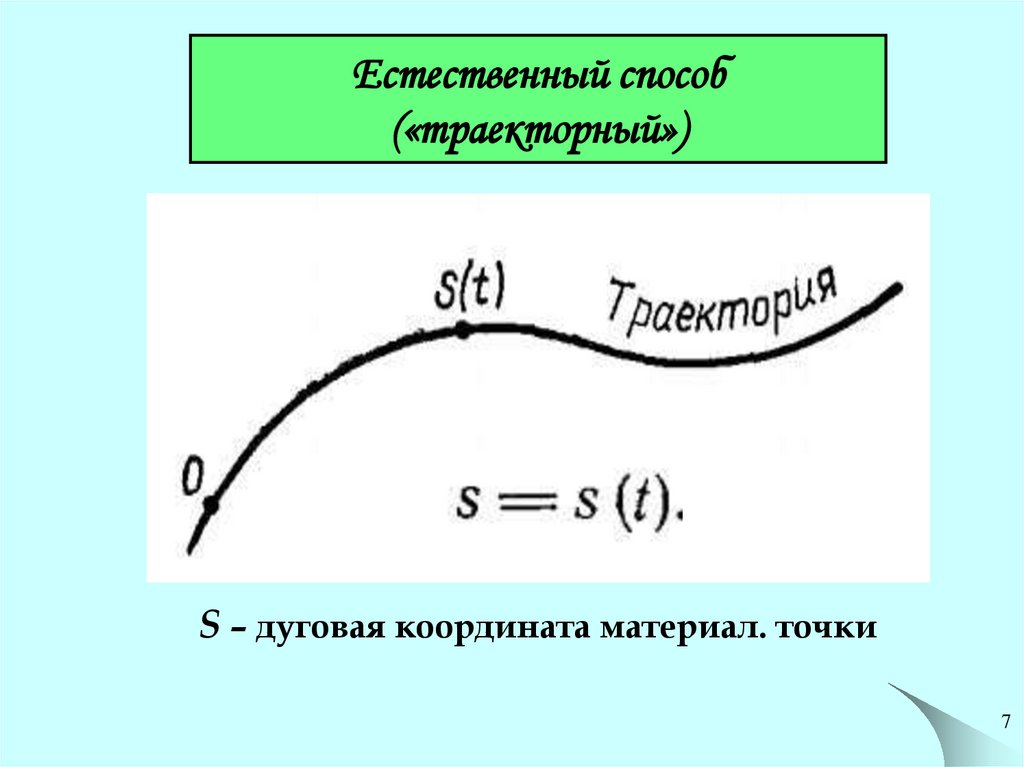
7. Естественный способ («траекторный»)

S – дуговая координата материал. точки
7

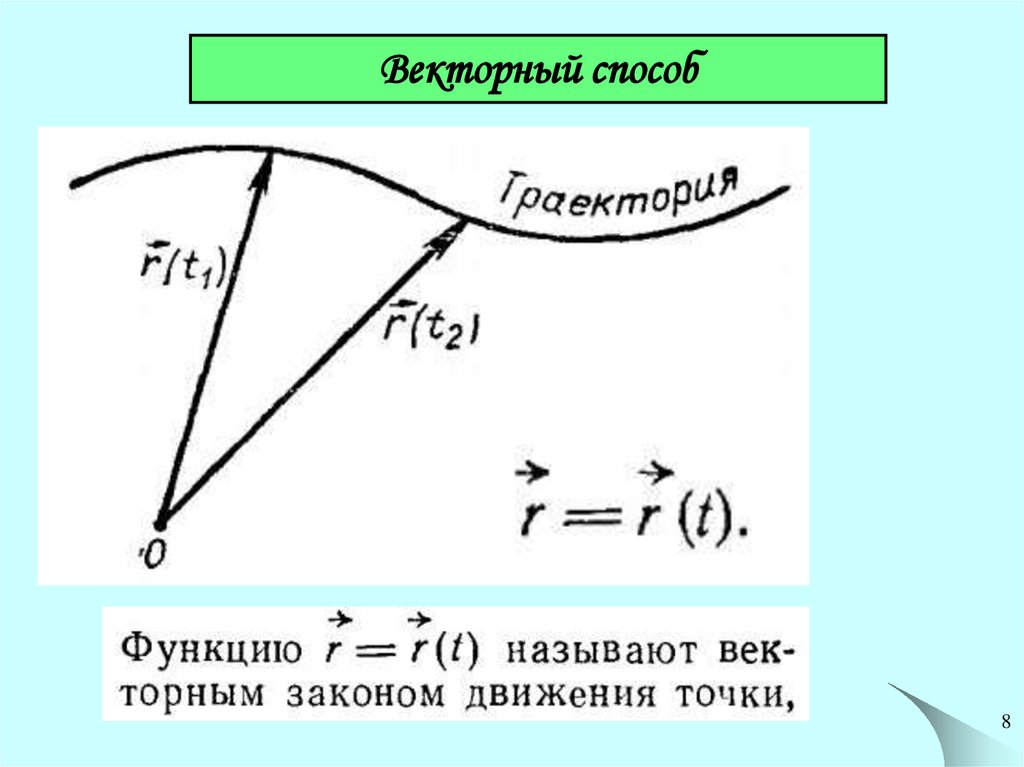
8. Векторный способ

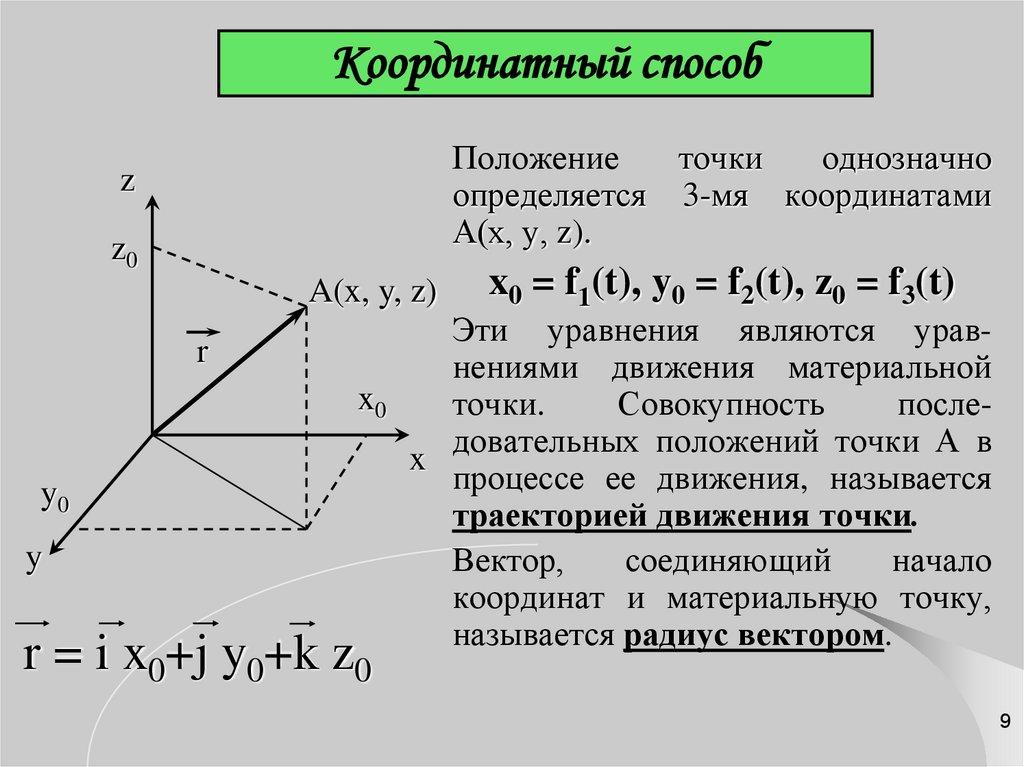
8

9. Координатный способ

Положение
точки
однозначно
определяется 3-мя координатами
А(х, у, z).
z
z0
A(x, y, z)
x0 = f1(t), y0 = f2(t), z0 = f3(t)
Эти уравнения являются уравнениями движения материальной
x0
точки.
Совокупность
последовательных положений точки А в
x
процессе ее движения, называется
y0
траекторией движения точки.
y
Вектор,
соединяющий
начало
координат и материальную точку,
называется радиус вектором.
r = i x0+j y0+k z0
r
9

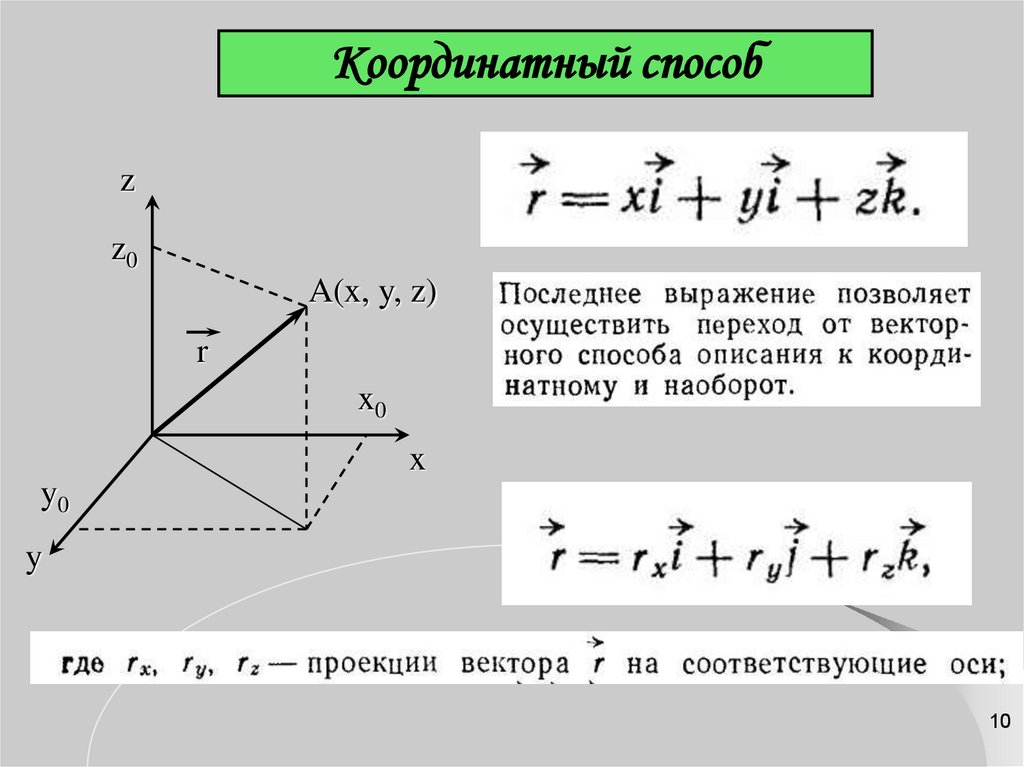
10. Координатный способ

z
z0
A(x, y, z)
r
x0
x
y0
y
10

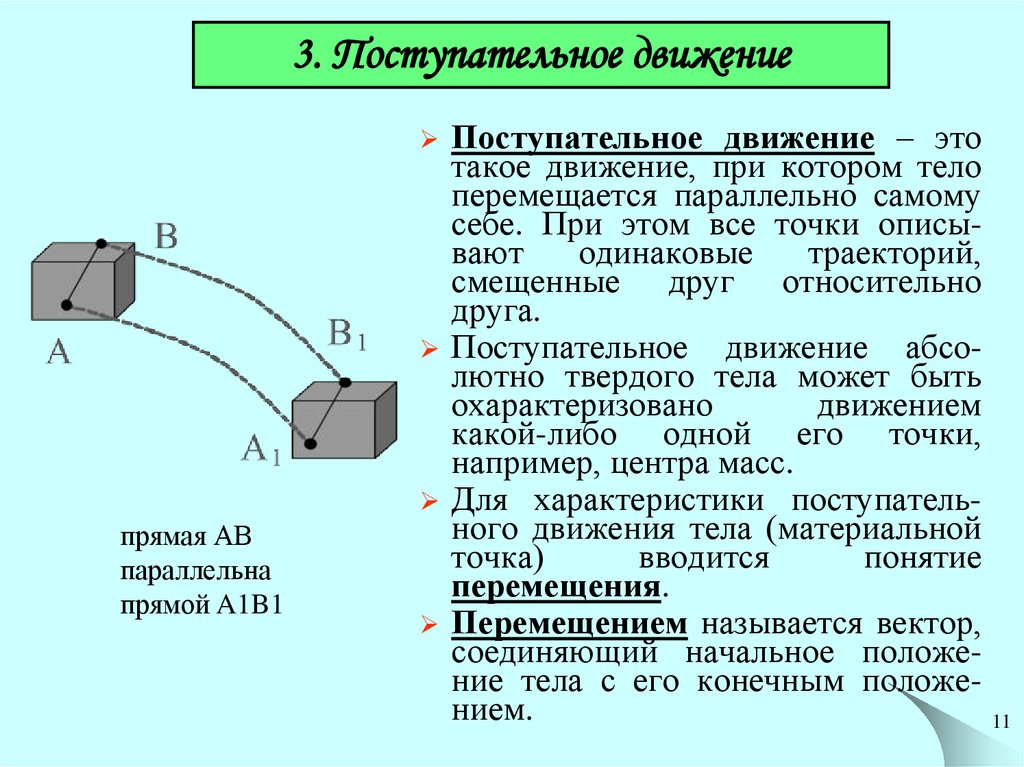
11. 3. Поступательное движение

Поступательное
прямая АВ
параллельна
прямой A1B1
движение – это
такое движение, при котором тело
перемещается параллельно самому
себе. При этом все точки описывают
одинаковые
траекторий,
смещенные друг относительно
друга.
Поступательное движение абсолютно твердого тела может быть
охарактеризовано
движением
какой-либо одной его точки,
например, центра масс.
Для характеристики поступательного движения тела (материальной
точка)
вводится
понятие
перемещения.
Перемещением называется вектор,
соединяющий начальное положение тела с его конечным положением.
11

12.

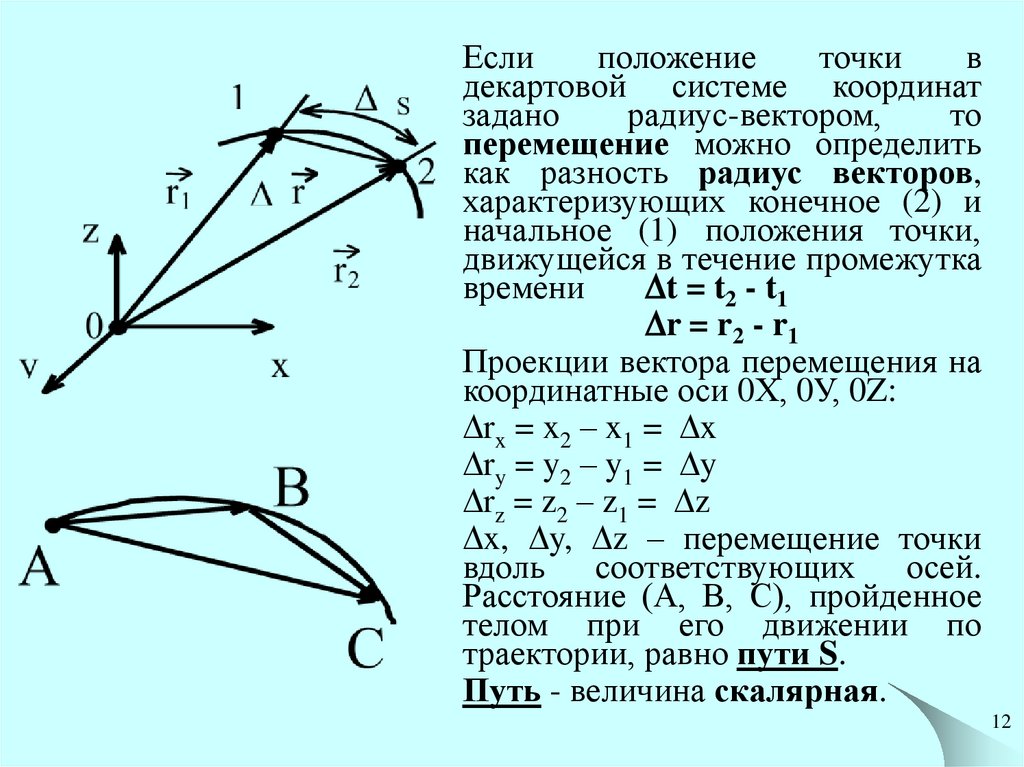
Если
положение
точки
в
декартовой системе координат
задано
радиус-вектором,
то
перемещение можно определить
как разность радиус векторов,
характеризующих конечное (2) и
начальное (1) положения точки,
движущейся в течение промежутка
времени
t = t2 - t1
r = r2 - r1
Проекции вектора перемещения на
координатные оси 0Х, 0У, 0Z:
rx = x2 – x1 = x
ry = y2 – y1 = y
rz = z2 – z1 = z
x, y, z – перемещение точки
вдоль соответствующих осей.
Расстояние (А, В, С), пройденное
телом при его движении по
траектории, равно пути S.
Путь - величина скалярная.
12

13.

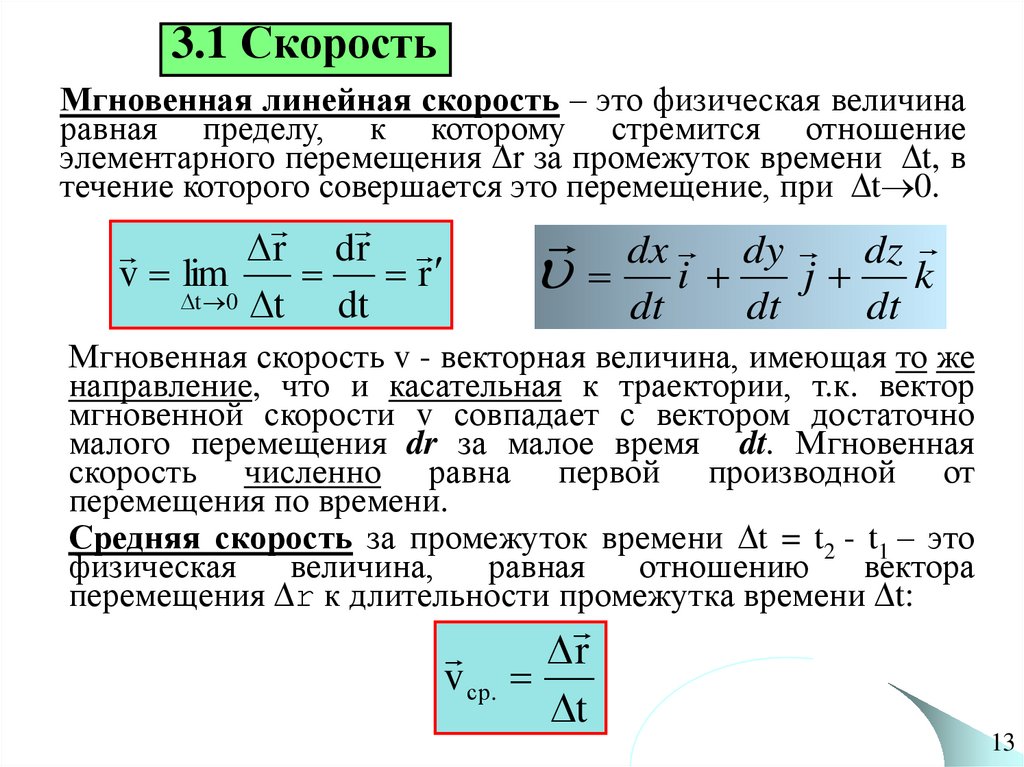
3.1 Скорость
Мгновенная линейная скорость – это физическая величина
равная пределу, к которому стремится отношение
элементарного перемещения r за промежуток времени t, в
течение которого совершается это перемещение, при t 0.
r dr
v lim
r
t 0 t
dt
dx dy dz
dt i dt j dt k
Мгновенная скорость v - векторная величина, имеющая то же
направление, что и касательная к траектории, т.к. вектор
мгновенной скорости v совпадает с вектором достаточно
малого перемещения dr за малое время dt. Мгновенная
скорость численно равна первой производной от
перемещения по времени.
Средняя скорость за промежуток времени t = t2 - t1 – это
физическая
величина,
равная
отношению
вектора
перемещения r к длительности промежутка времени t:
r
v ср.
t
13

14.

Средняя скалярная (путевая) скорость - физическая
величина, определяемая отношением пути S, пройденного
точкой за промежуток времени t к длительности этого
промежутка:
S
v ср .
t
t2
следовательно
dS v dt и
S v dt
t1
v
График функции
v = f(t)
Величину пройденного точкой
пути
можно
представить
графически
как
площадь
фигуры, ограниченной кривой:
v = f(t), прямыми t = t1 и t = t2 и
осью времени на графике
скорости.
Путь = площади
под кривой
0
t = t1
t = t2
t
14

15.

3.2 Ускорение
При движении точки мгновенная скорость может меняться как
по величине, так и по направлению. При этом вектор v
стремится к некоторому пределу, называемому линейным
ускорением:
v dv d d r
a lim
t 0 t
dt dt dt
Ускорение - векторная величина, характеризующая
изменение скорости в единицу времени, численно равная
первой производной от мгновенной скорости по времени или
второй производной от перемещения по времени.
Вектор ускорения а представляют в виде 2-х взаимно
перпендикулярных векторов: аn – нормального ускорения
(перпендикуляр к траектории), аt – тангенциального ускорения
(по касательной к траектории).
dt
d ( t ) d
a
t
15
dt
dt
dt

16.

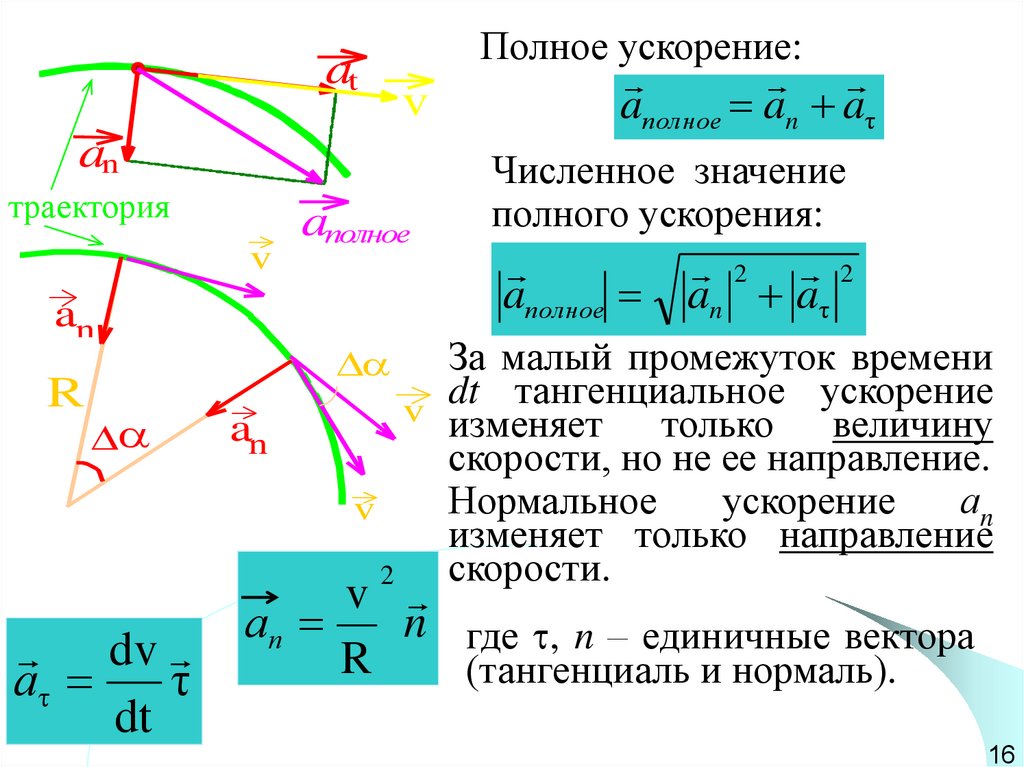
at
Полное ускорение:
v
an
траектория
v
an
R
dv
аτ
τ
dt
aполное
aполное an aτ
Численное значение
полного ускорения:
aполное
2 2
an aτ
За малый промежуток времени
dt
тангенциальное
ускорение
v изменяет
только величину
скорости, но не ее направление.
Нормальное
ускорение
аn
v
изменяет только направление
скорости.
2
an
v
ап
n где t, n – единичные вектора
R
(тангенциаль и нормаль).
16

17.

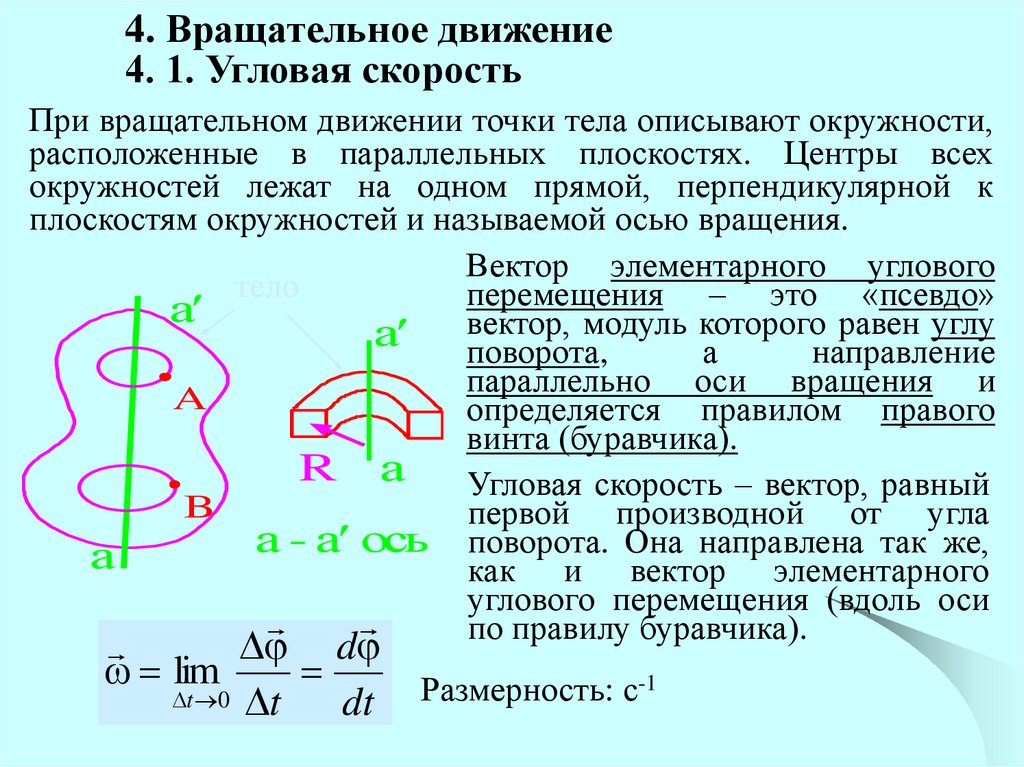
4. Вращательное движение
4. 1. Угловая скорость
При вращательном движении точки тела описывают окружности,
расположенные в параллельных плоскостях. Центры всех
окружностей лежат на одном прямой, перпендикулярной к
плоскостям окружностей и называемой осью вращения.
Вектор элементарного углового
тело
перемещения – это «псевдо»
а
модуль которого равен углу
а вектор,
поворота,
а
направление
параллельно оси вращения и
A
определяется правилом правого
винта (буравчика).
R а
Угловая скорость – вектор, равный
B
первой производной от угла
а - а ось поворота. Она направлена так же,
а
как и вектор элементарного
углового перемещения (вдоль оси
по правилу буравчика).
d
lim
-1
Размерность:
с
t 0 t
dt

18.

d
d
S
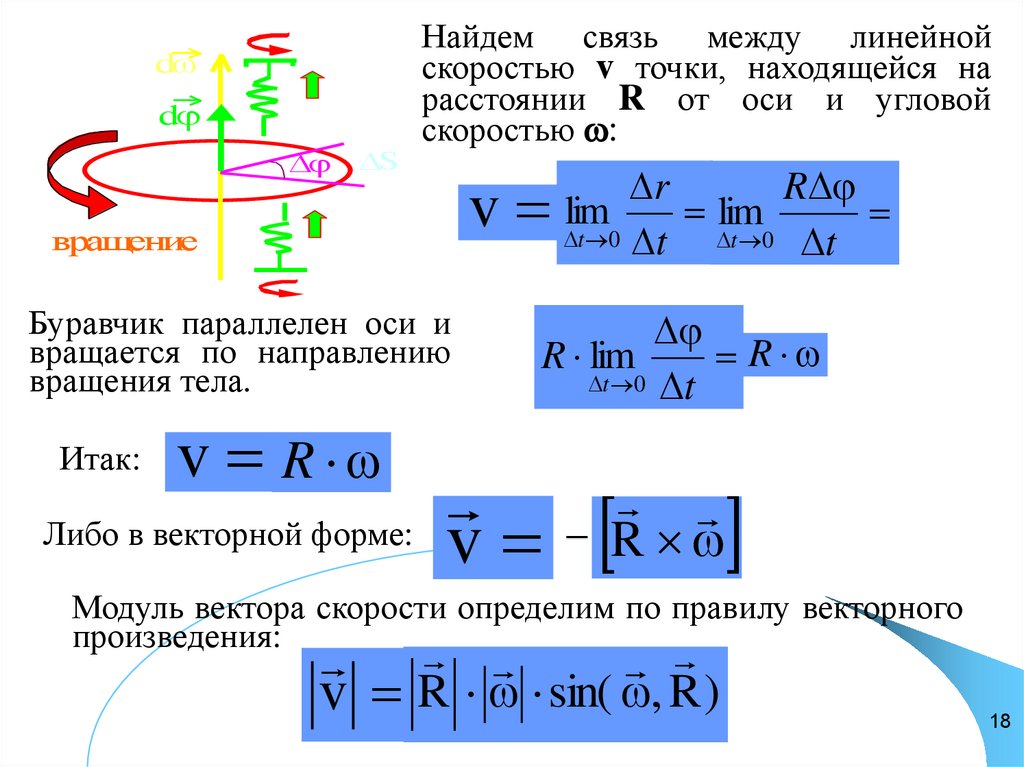
Найдем связь между линейной
скоростью v точки, находящейся на
расстоянии R от оси и угловой
скоростью :
вращение
Буравчик параллелен оси и
вращается по направлению
вращения тела.
Итак:
v R
r
R
lim
v lim
t 0 t
t 0 t
R lim
R
t 0 t
Либо в векторной форме:
v
R
Модуль вектора скорости определим по правилу векторного
произведения:
v R sin( , R )
18

19.

Направление скорости V определяется
правилом правого винта (буравчика).
Π/2
Винт располагаем перпендикулярно оси
0
и вращаем от к R.
v
R
Таким образом, чем дальше отстоит
точка от оси вращения, тем больше ее
линейная скорость.
При =const существует время полного оборота тела.
Период вращения Т – это время за которое совершается телом
один полный оборот. При этом:
d 2
dt
Т
2
Т
Число оборотов в единицу
времени есть частота вращения.
d 2 (360 )
dt Т
1
ν
Т 2
2 ν

20.

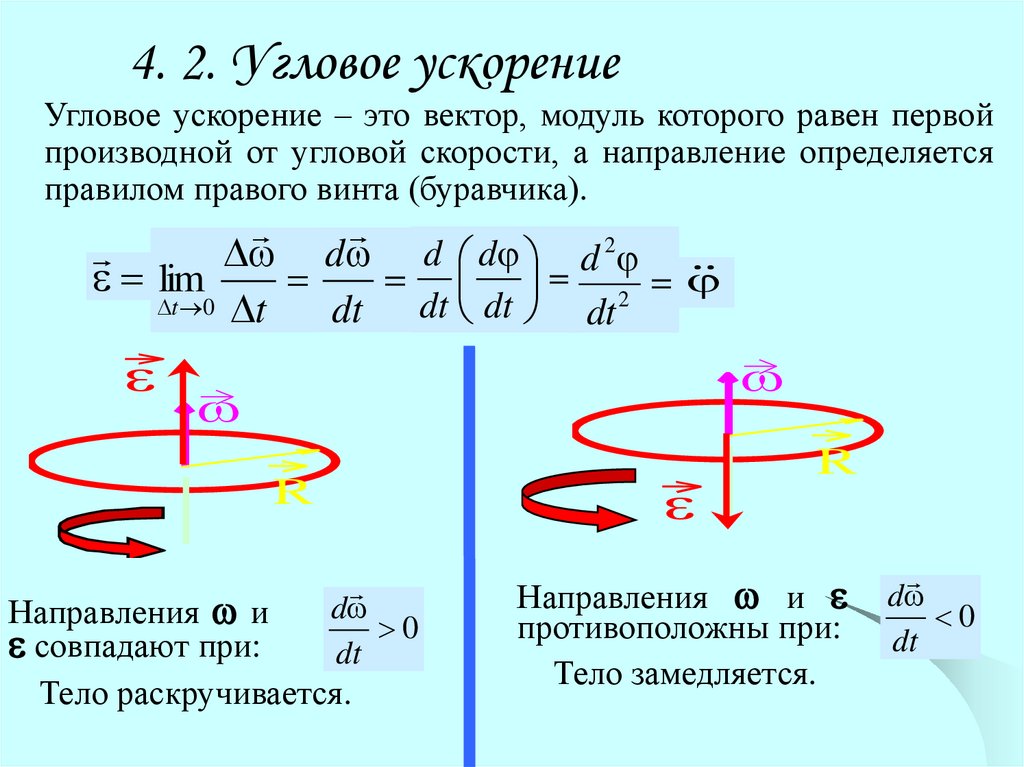
4. 2. Угловое ускорение
Угловое ускорение – это вектор, модуль которого равен первой
производной от угловой скорости, а направление определяется
правилом правого винта (буравчика).
d d d d 2
lim
2
t 0 t
dt dt dt dt
R
d
0
dt
Направления и
совпадают при:
Тело раскручивается.
R
Направления и
противоположны при:
Тело замедляется.
d
0
dt

21.

Найдем связь между линейными ускорениями и угловыми:
d
d R
dv
R
v R
R
аτ
dt
dt
dt
v 2 2 R 2
2
аn
n v R
n R
R
R
Итого:
аτ R
2
аn R
S R
v R
При =const :
0 t
аполное R 2 R
t 2
0 0t
2
21

22.

22