Similar presentations:
Предмет механики
1. Предмет механики
Механика – часть физики, которая изучаетзакономерности механического движения и
причины, вызывающие или изменяющие это
движение.
Механическое движение – это изменение с
течением времени взаимного расположения
тел или их частей.
1
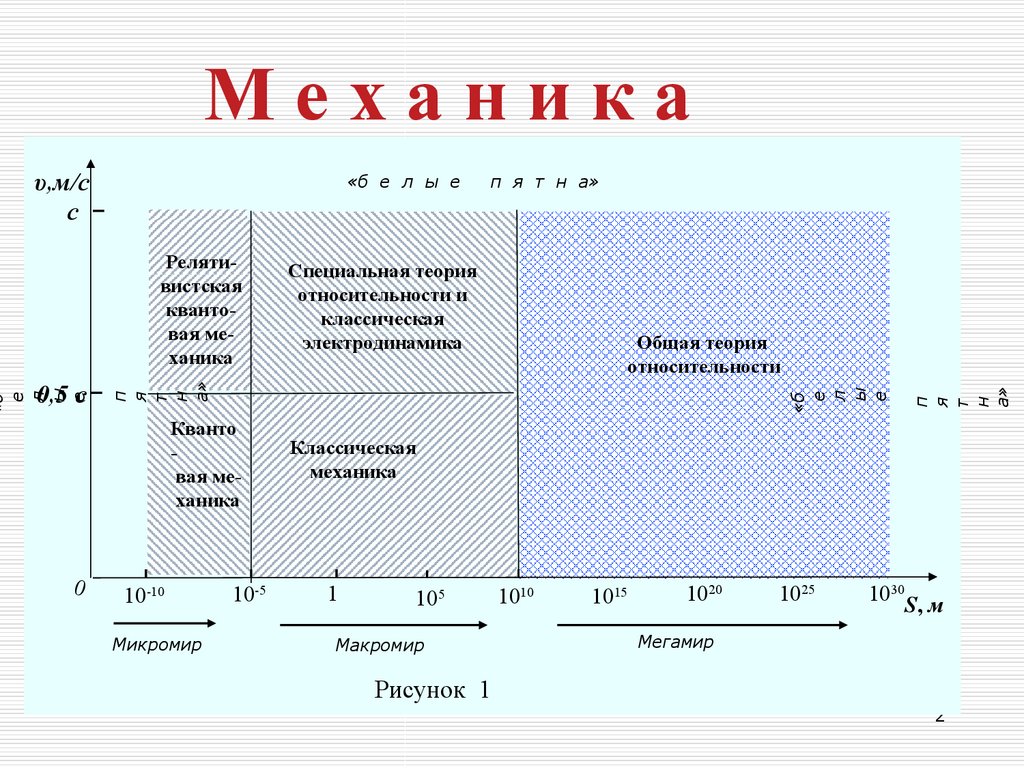
2.
Механика«б е л ы е
υ
Общая теория
относительности
«б
е
л
ы
е
«б
е
л
ы
е
Кванто
вая механика
0
Специальная теория
относительности и
классическая
электродинамика
п
я
т
н
а»
Релятивистская
квантовая механика
0,5 с
п я т н а»
10-10
Микромир
10-5
п
я
т
н
а»
υ,м/с
с
Классическая
механика
1
105
Макромир
1010
1015
1020
1025
1030
S, м
Мегамир
Рисунок 1
2
3. Классическая механика
Кинематикаизучает движение тел, не
рассматривая причины, которые вызывают или
изменяют это движение.
Динамика изучает законы движения тел и
причины, которые вызывают или изменяют это
движение.
Статика изучает законы равновесия системы
тел.
3
4. Основные понятия
Материальная точка это тело, размерами иформой которого в данной задаче можно
пренебречь.
Абсолютно твердым телом называется тело,
расстояние между любыми точками которого не
меняется со временем.
Абсолютно твердое тело, с которым связывают
ту или иную систему координат, условно
считают неподвижным и относительно
которого исследуют движение других тел,
называется телом отсчета.
4
5. Система отсчета
Совокупность системы координат, жесткосвязанной с телом отсчета, часов для отсчета
времени с указанием начала отсчета времени
называется системой отсчета.
Радиус-вектор
Вектор, проведённый из
точки отсчёта к положению
движущегося тела в данный
момент времени называется
радиус – вектором.
r (t)
О
5
6. Траектория, путь, вектор перемещения
Линия, которую описывает материальнаяточка, перемещаясь в пространстве,
называется траекторией.
Алгебраическая сумма длин траекторий,
описанных точкой к данному моменту
времени, называется длиной пути (∆S).
Вектор, проведённый из
начальной точки в конечную
точку пути называется
вектором перемещения (∆r) .
ΔЅ
r0
∆r
r
О
6
7. Способы описания движения
1) Векторный способописания движения:
r (t)
r r (t )
О
2)Координатный способ:
z
кинематические
x = x(t)
y = y(t) - уравнения
движения
z = z(t)
f (x, y, z) = 0 – траектория
движения
3)Параметрический
способ: S = S(t)
О
M (x, y, z)
r (t )
у
х
r i x j y k z
(1)
7
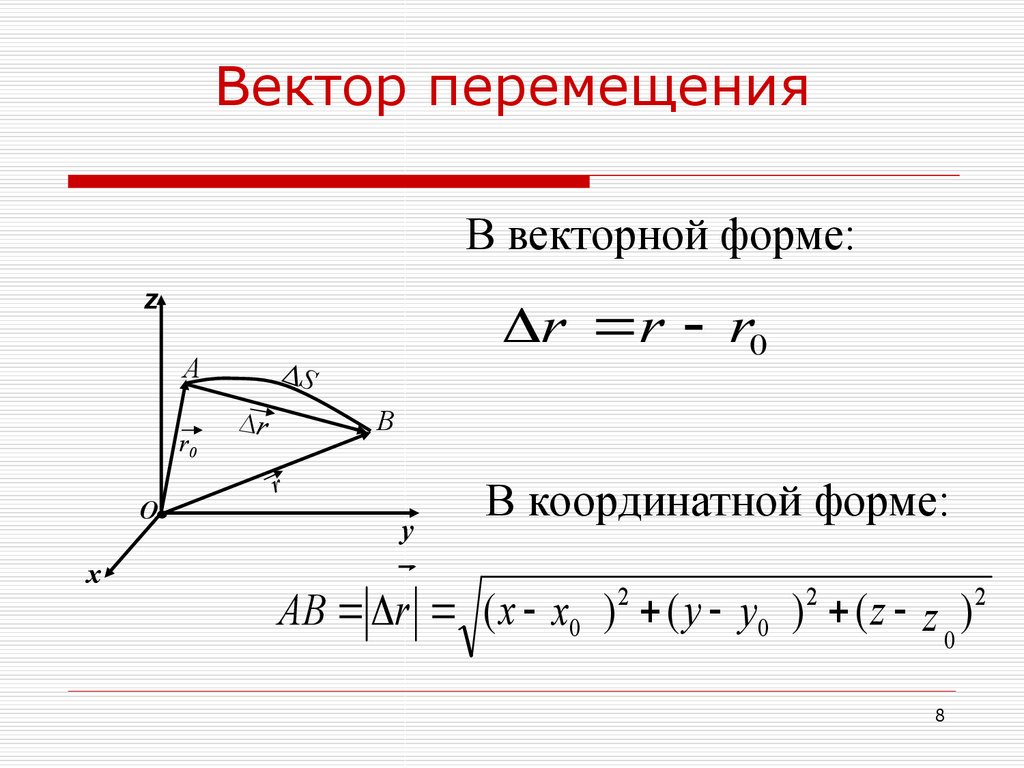
8. Вектор перемещения
В векторной форме:r r r0
z
А
r0
О
х
ΔЅ
В
∆r
r
у
В координатной форме:
AB r ( x x0 ) 2 ( y y0 ) 2 ( z z ) 2
0
8
9. Скорость
Скорость - векторная величина, определяющаябыстроту и направление движения.
Средняя скорость перемещения:
r
t
М
<υ>
Средняя путевая скорость :
S
S
t
Мгновенная скорость:
r dr
lim
t 0 t
dt
ΔЅ
υ1
М
dr dS
dt
dt
N
Δr
ΔЅ
τ
Δr
(2)
N
τ
9
υ2
10. Задание скорости в координатной форме
Из формул (1) и (2) следует:dx dy dz
i
j k x i y j z k
dt
dt
dt
2x 2y 2z
dx 2 dy 2 dz 2
dt
dt
dt
10
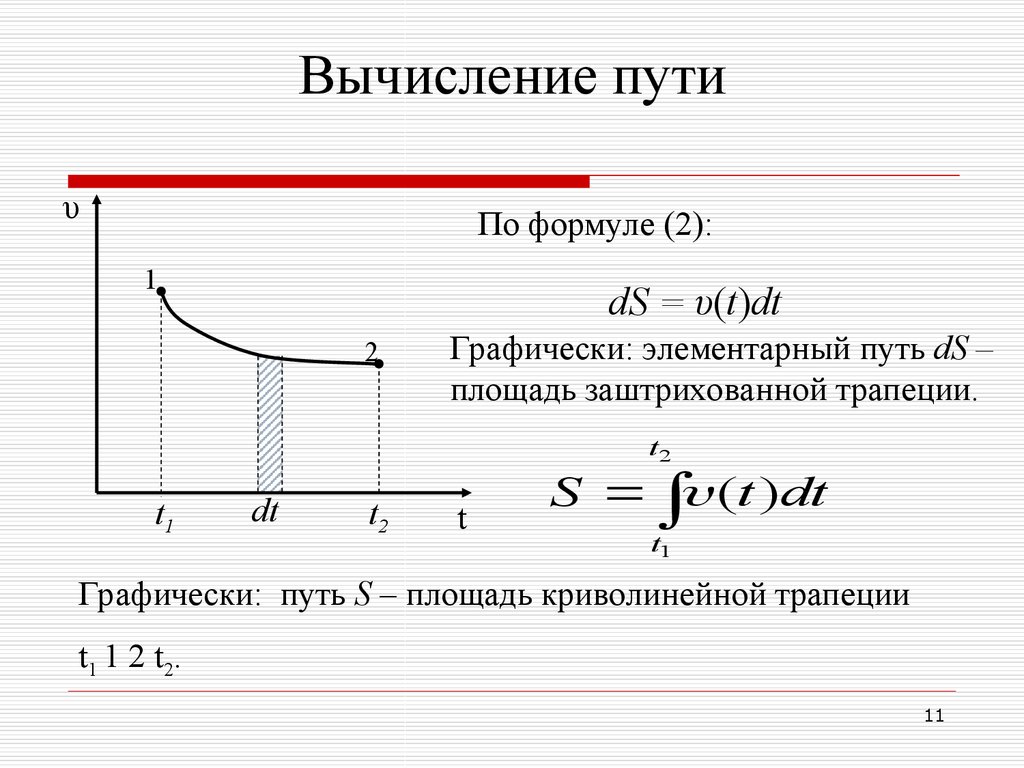
11. Вычисление пути
υПо формуле (2):
1
dS = υ(t)dt
2
Графически: элементарный путь dS –
площадь заштрихованной трапеции.
t2
t1
dt
t2
t
S
(t ) dt
t1
Графически: путь S – площадь криволинейной трапеции
t1 1 2 t2.
11
12. Ускорение
Ускорение - это физическая величина, характеризующаябыстроту изменения вектора скорости по величине и
направлению.
Среднее ускорение:
a
t
υ1
Мгновенное ускорение:
М
d
a lim
t 0 t
dt
Δυ
2
N
υ2
d 2r d 2 x d 2 y d 2 z
a 2 2 i 2 j 2 k
dt
dt
dt
dt
2
ΔЅ
2
2
2
d x d y d z
2
2
2
a a x a y a z 2 2 2
dt dt dt
υ2
2
12
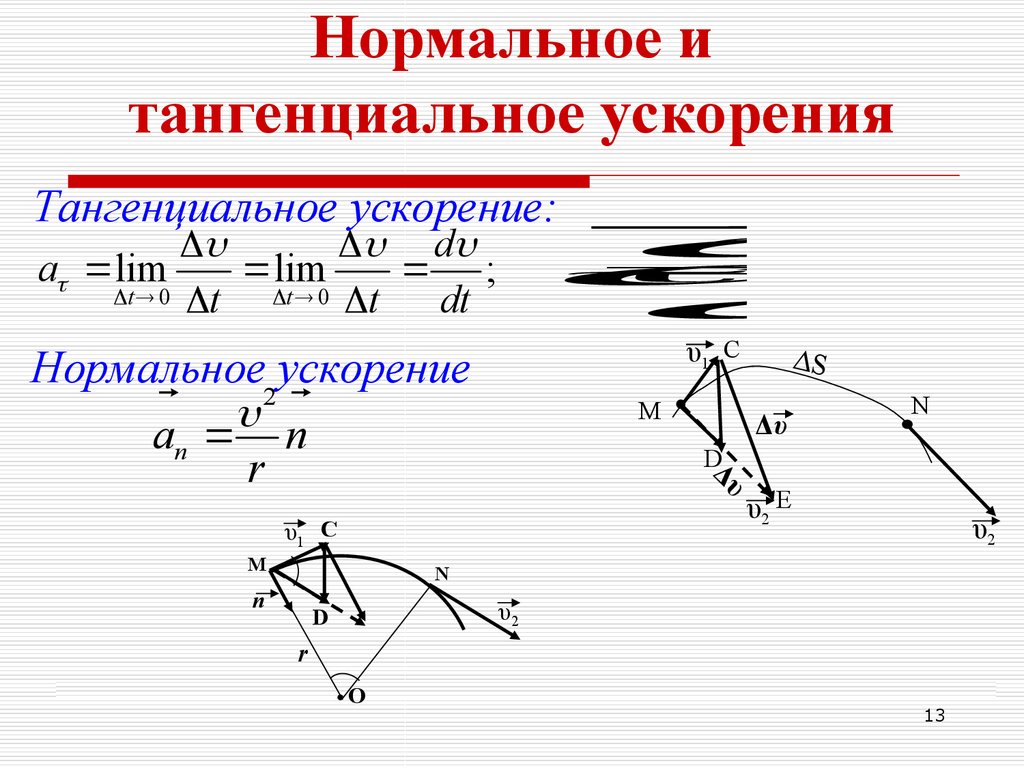
13. Нормальное и тангенциальное ускорения
Тангенциальное ускорение:d
d
a lim
lim
; a
=
t 0 t
t 0 t
dt
dt
υ С
ΔЅ
Нормальное2 ускорение
N
М
Δυ
a n
1
n
r
DΔ
υ1 С
М
υ
υ2 Е
υ2
N
п
υ2
D
r
О
13
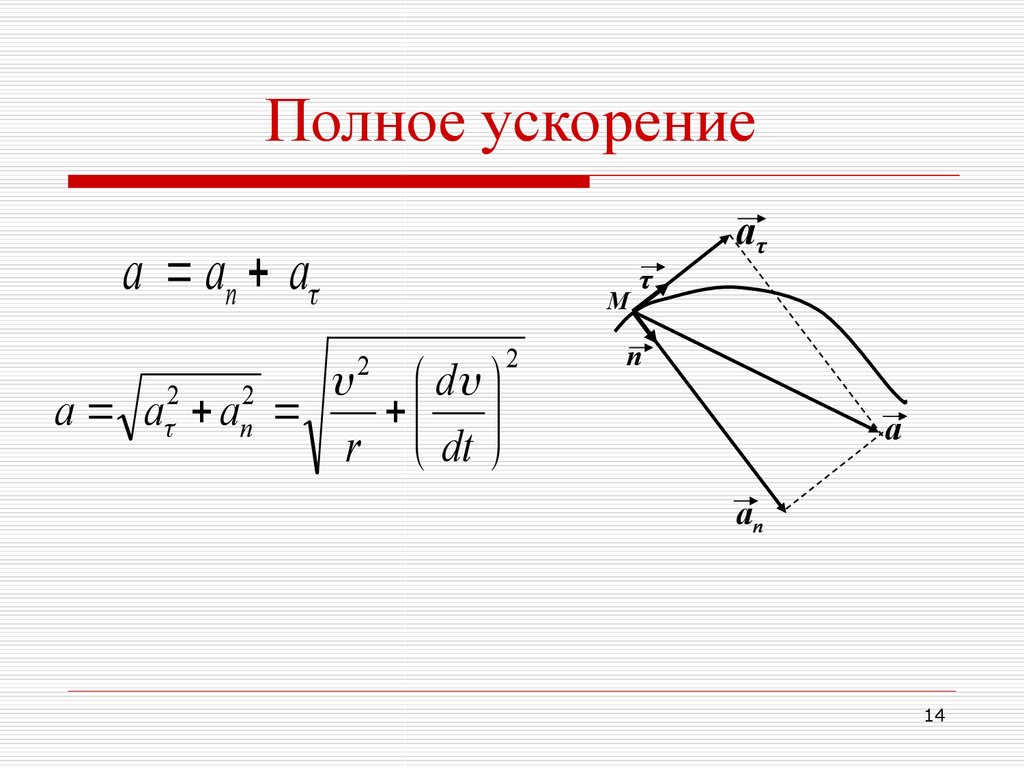
14.
Полное ускорениеаτ
a an a
М
2
d
a a a
r dt
2
2
n
2
τ
п
а
ап
14
15. Поступательное и вращательное движения
Поступательное движение – это движение, при которомлюбая прямая, жестко связанная с движущимся телом,
остается
параллельной
своему
первоначальному
положению.
Вращательное движение – это движение, при котором все точки
тела движутся по окружностям, центры которых лежат на одной
прямой, называемой осью вращения.
Средняя угловая скорость
t
d
Мгновенная угловая скорость
dt
15
16. Угловая скорость
Направление вектора угловой скорости находится поправилу буравчика (правилу правого винта).
Единица угловой скорости: рад/с,
S
R
lim
R lim
R
Линейная скорость lim
t 0 t
t 0 t
t 0 t
В векторной форме
[ R ]
Период вращения
Частота вращения
r
2
T
1
n ;
T 2
Δφ
2 n
ΔЅ
16
17. Угловое ускорение
Среднее угловое ускорениеt
d
Мгновенное угловое ускорение
dt
Единица углового ускорения рад/с.2
При ускоренном
движении
вектор
сонаправлен
век
тору , при замедленном – противоположен ему.
Ускоренное вращение
17
Замедленное вращение
18. Связь между линейными и угловыми величинами
S= R ;= R ;
a = R ;
an = 2R.
В случае равнопеременного движения точки по
окружности ( = const):
0 t
t2
0t
2
ω – ω0 = 2εφ
2
2
18













 physics
physics mechanics
mechanics








