Similar presentations:
Физические основы механики молекулярная физика. Основы термодинамики
1. ФИЗИКА Ч.1
ФИЗИЧЕСКИЕ ОСНОВЫМЕХАНИКИ
МОЛЕКУЛЯРНАЯ ФИЗИКА.
ОСНОВЫ ТЕРМОДИНАМИКИ
2. Дисциплина «Физика»
Лекцию читаетКандидат физико-математических
наук, доцент
Кузьмин Юрий Ильич
3. Структура дисциплины «физика»
Часть 1.Физические основы механики.
Молекулярная физика и термодинамика.
Электромагнетизм.
Часть 2.Колебания и волны.
Часть 3.Квантовая теория излучения.
Элементы квантовой механики.
Физика атома и ядра.
4. ЗАДАНИЯ НА КОНТРОЛЬНЫЕ РАБОТЫ по первой части
• КР №1 Физические основы механики• КР №2 Молекулярная физика. Основы
термодинамики
2003 и др. годы издания
5. Рекомендуемая литература
• 1. Трофимова Т.И. Курс физики. - М.: Высш. шк., 2003и др. годы.
• 2. Детлаф А.А., Яворский Б.М. Курс физики.- М.:
Высш. шк., 2001 и др. годы.
• 3. Трофимова Т.И., Павлова З. Г. Сборник задач по
курсу физики с решениями. - М.: Высш. шк., 1999 и
др. годы.
• 4. Цаплев В. М. и др. Курс физики. Физические
основы механики. Молекулярная физика и
термодинамика: Учебное пособие. – СПб.: Изд-во
СЗТУ, 2006.
6. Электронные адреса
• Задания на контрольные работы иучебные пособия издания СЗТУ можно
найти на сайте университета:
www.nwpi.ru
• Вопросы по курсу физики и
контрольным работам можно задавать
преподавателям кафедры по
электронной почте: physics@ nwpi.ru
7. Тема I. Кинематика 1. Кинематика поступательного движения
• Материальная точка – это тело, размерамикоторого можно пренебречь в данной
задаче.
Система отсчёта- тело,которое
условно считаем
неподвижным;связанная с ним
система координат и часы.
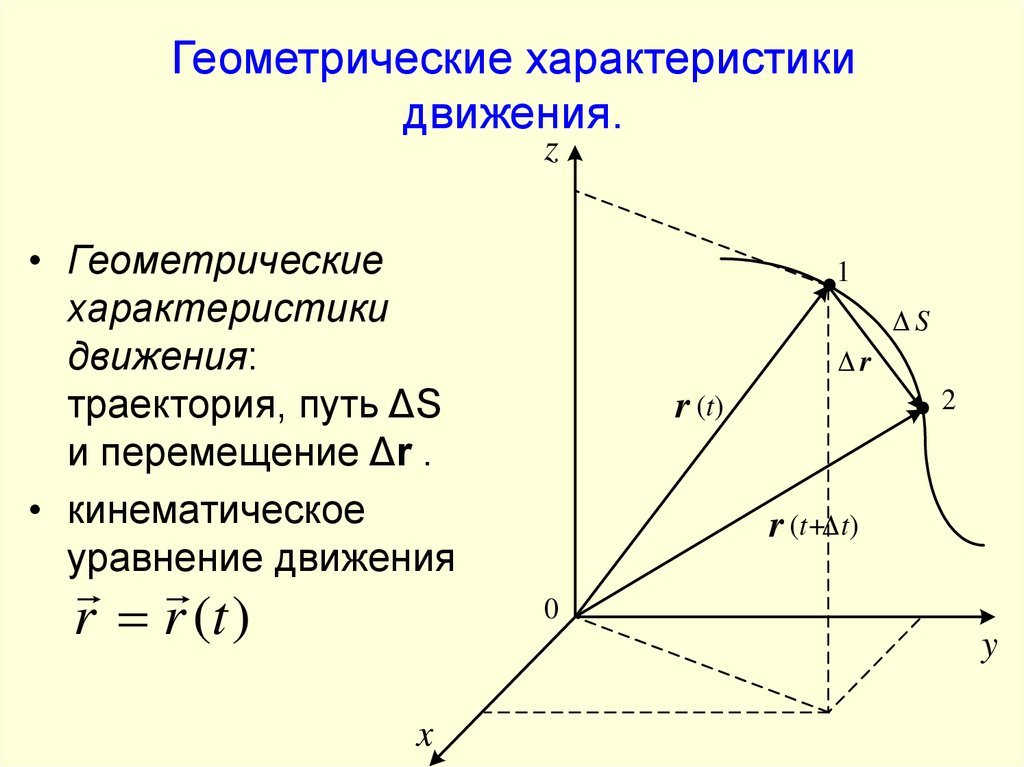
8. Геометрические характеристики движения.
z• Геометрические
характеристики
движения:
траектория, путь ΔS
и перемещение Δr .
• кинематическое
уравнение движения
r r (t )
1
S
r
2
r (t)
r (t+ t)
0
y
x
9. Кинематические характеристики движения
• Скорость – характеризует быстротуперемещения точки по траектории:
• Средняя скорость .
r
v
t
.
• Направлена по вектору перемещения.
(1)
Мгновенная скорость
r dr
v lim
t 0
t dt (2)
направлена по касательной к траектории.
10. Ускорение
va
t
• Среднее ускорение
(3)
• Мгновенное ускорение точки в момент
времени t
(4)
v dv
a lim
t 0
t dt
11.
• Разложим полный вектор ускорения на двесоставляющие:
а аn а
• В случае произвольного криволинейного движения:
dv
а
dt
• Касательная составляющая ускорения характеризует
изменение скорости по величине.
• Нормальное (центростремительное) ускорение
v
аn
R
2
• R – радиус кривизны траектории.
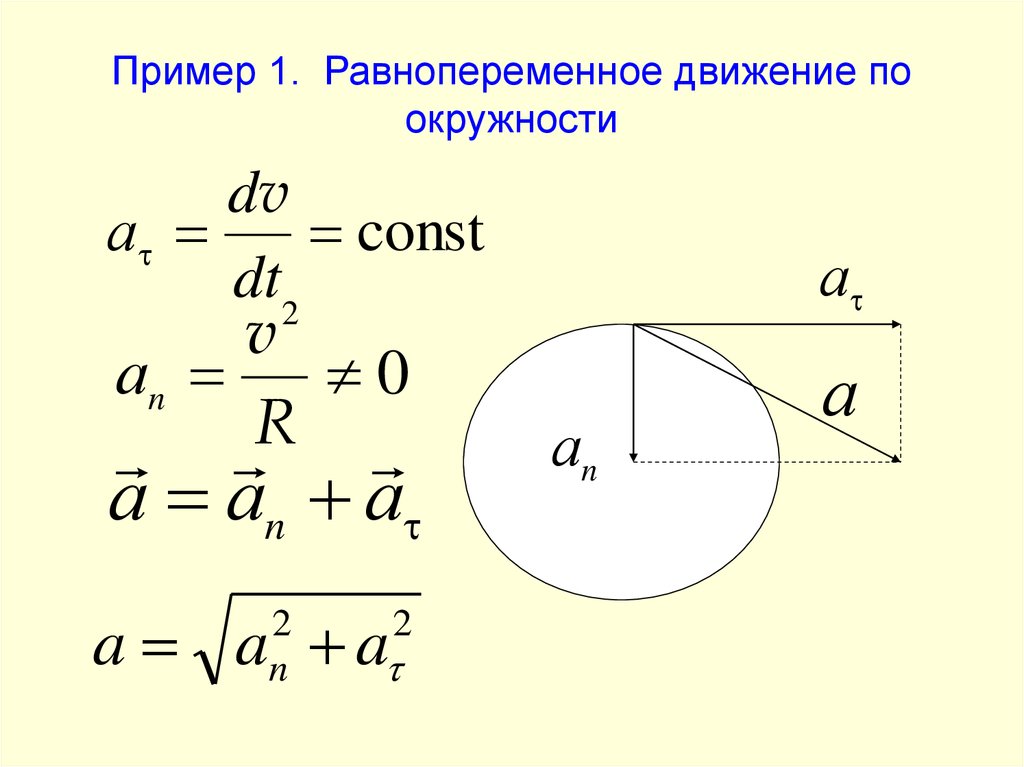
12. Пример 1. Равнопеременное движение по окружности
dvа
const
dt2
v
аn
0
R
а аn а
a a a
2
n
2
а
аn
а
13. Задача
Материальная точка движется вдольоси Х согласно уравнению ,
Х А Вt Сt Dt
2
3
где С = 1 м/с2; D = -0,2 м/c3.
Определить, в какой момент времени
ускорение равно нулю.
14. Дано:
Х А Вt Сt Dt2
С = 1 м/с2
D = -0,2 м/c3
___________________
t = ? (а = 0)
3
15. Решение:
dv•а
dt
Решение:
dx
2
v
В 2Сt 3Dt
dt
dv
a
2С 6Dt 0
dt
1C
1
t
1,67 с
3D 3 0,2
16. 2. Кинематика вращательного движения твёрдого тела
• Закономерности вращательного движениярассматриваем на простейшей модели –
абсолютно твёрдом (недеформируемом)
теле, вращающимся вокруг неподвижной оси.
• При вращении все его точки описывают
окружности вокруг одной прямой - оси
вращения.
Если тело за время t поворачивается на
угол , то угловая скорость определяет
быстроту изменения угла поворота во
времени:
17.
t
Мгновенное значение:
• Среднее значение:
d
lim
t 0 t
dt
(5)
(6)
• Направление вектора угловой скорости
определяется правилом правого винта:
вектор направлен так же, как направлен
винт с правой резьбой при завинчивании,
причем направление вращения винта
совпадает с направлением вращения
тела.
18. Угловое ускорение
t• Среднее значение
d
lim
t 0 t
dt
• Мгновенное значение
(7)
(8)
• Связь линейных и угловых величин
при малых Δt
r ~ R
r
v lim
R lim
R
t 0 t
t 0 t
(9)
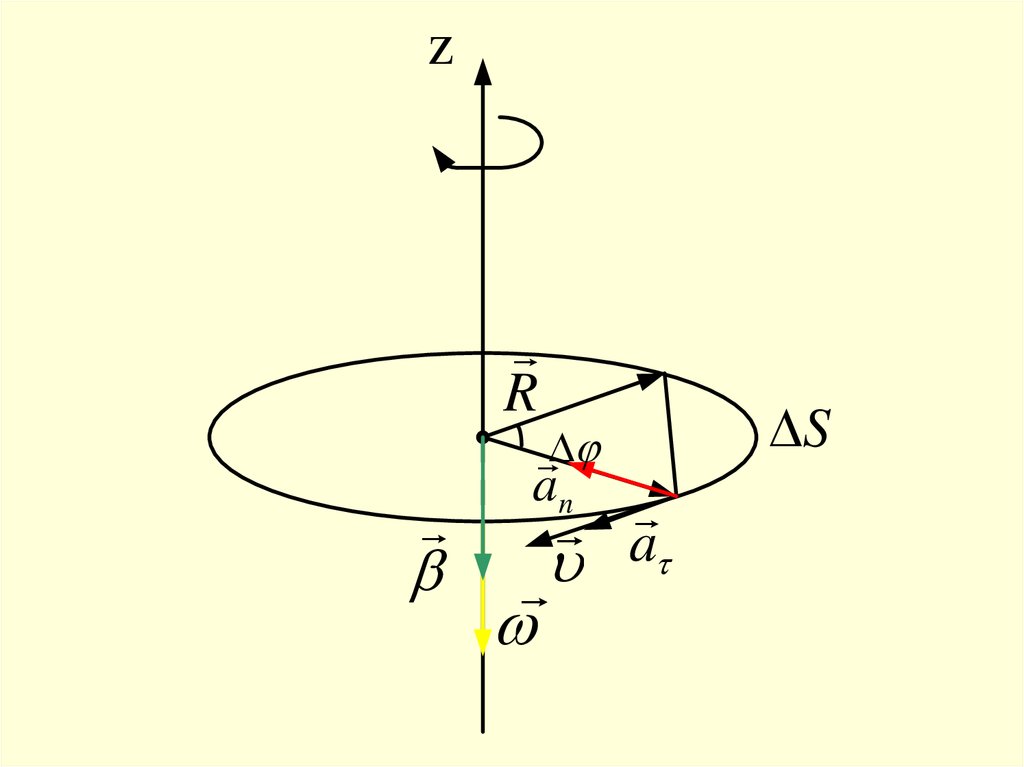
19.
zR
S
an
a
20.
• Касательное ускорениеdv
d
a
R
R
dt
dt
(10)
• Нормальное ускорение
v
R
2
an
R
R
R
2
2
2
(11)
При равномерном вращении
2
2 n
T
1
Где n
– число полных оборотов тела за 1
T
21.
• Пример: 1. Чему равно центростремительное(аn) ускорение точек земной поверхности на
полюсе? Линейная скорость точки земной
поверхности, находящейся на
полюсе
,
v
0
2
v
следовательно
.
аn
0
• 2. На экваторе
R
• линейная скорость точки
2 R3
v
T
4
8
,
64
10
• где Rз – радиус Земли, Т =
c = 24 ч.
v
аn
Rз
2
22. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
• 1. Законы Ньютона• Первый закон Ньютона: существуют такие
системы отсчета, в которых тело сохраняет
состояние покоя или равномерного
прямолинейного движения до тех пор, пока
на него не подействуют другие тела. Такие
системы называются инерциальными
23.
• Второй закон Ньютона: ускорениематериальной точки прямо
пропорционально вызывающей его силе и
обратно пропорционально
массе тела:
F
а
m
(1)
• F – векторная сумма всех сил, действующих
на тело.
• Сила характеризует количественное
воздействие на тело со стороны других тел и
направление этого воздействия; m
определяет инерционные свойства тела, т.е.
реакцию тела на это воздействие.
24.
•р mv – импульс тела(2)
dv d (mv) dp
F ma m
dt
dt
dt(3)
dp
F
dt
• C учетом выражения
(2):
Выражение (3) – это более общая
формулировка второго закона Ньютона. Его
формулировка: Скорость изменения
импульса тела равна результирующей
всех приложенных к телу сил.
25. Виды сил
• В механике изучают следующие виды сил.– 1.Сила тяготения вычисляется по закону всемирного
тяготения:
m1m2
F G 2
r
– Вблизи поверхности Земли тела приобретают ускоре–
–
–
–
ние свободного падения g. P = mg
-сила тяжести.
2.Сила трения возникает при относительном
перемещении тел
тр
-коэффициент трения скольжения.
3.Сила упругости при малых деформациях вычисляет-ся
по закону Гука:
F N mg
F -kx
26.
• Третий закон Ньютона:силы, с которыми
взаимодействуют две
материальные точки, всегда
равны по модулю,
противоположны по
направлению и действуют
вдоль прямой, соединяющей
эти точки
Существенно, что эти силы,
приложенные к разным
телам, всегда действуют
парами и являются силами
одной природы.
f12 f 21
27. Задача
• Мяч массой 0,5 кг после удара,длящегося 0,02 с, приобретает
скорость 10 м/с. Найти среднюю силу
удара.?
28. Дано:
m 0,5 кгv 10 м/c
t 0,02 c
F ?
29. Решение
• II закон Ньютона• 1) .
P m v
F
t
t
2) Вычисления
m v 0,5 10
2
F
2
,
5
10
Н
2
t
2 10
30.
• 2. Закон сохранения импульса• Основные понятия:
• 1. Система тел – это совокупность
взаимодействующих тел (материальных
точек), движение которых рассматривается
вместе и одновременно.
• 2. Силы, действующие между телами самой
механической системы, называются
внутренними силами. Силы, с которыми на
материальные точки системы действуют
внешние тела, называются внешними.
• 3. Система тел, на которую не действуют
внешние силы или действием внешних сил
можно пренебречь по сравнению с
внутренними силами, называется замкнутой
(или изолированной) механической системой.
31.
• 3. Закон сохранения импульса• Импульс системы тел Рc Р1 Р2 равен
векторной сумме импульсов тел, входящих в
систему.
• суммарный импульс замкнутой системы
тел сохраняется постоянным при любых
процессах, происходящих внутри
системы.
Рc соnst
(4)
Вывод закона сохранения импульса основан
на применении второго и третьего законов
Ньютона.
32.
• Между телами действуют внутренние силы f1и f 2 и внешние силы F и F .
1
2
• Запишем второй закон
Ньютона для каждого
тела:
d(m v )
f1 F1
dt
d(m2 v2 )
f 2 F2
dt
Сложим почленно эти уравнения
и получим
dPc
d
(m1 v1 m2 v 2 )
F1 F2
dt
dt
1 1
(5)
(6)
так как геометрическая сумма внутренних сил
по третьему закону Ньютона равна нулю.
33.
• При отсутствии внешних сил (рассматриваемзамкнутую систему)
(7)
dPc
0
dt
n
Рc mi vi const
(8)
i 1
• Это и есть закон сохранения импульса,
утверждающий, что импульс замкнутой
системы сохраняется, т.е. не изменяется с
течением времени.
34.
• Методика решения задач на законсохранения импульса
• 1. Для замкнутой системы тел записывается
закон сохранения импульса в векторной
форме.
• 2. Выбирают направление осей координат и
проецируют на них обе части векторного
уравнения. Т.е. необходимо приравнять
суммарный импульс замкнутой системы тел
до и после взаимодействия.
35.
• Пример на закон сохраненияимпульса
• Явление отдачи.
• До выстрела и пушка и снаряд покоились, т.е.
суммарный импульс системы пушка-снаряд
был равен нулю.
• В момент выстрела внутренняя сила – сила
давления пороховых газов значительно
больше всех внешних сил и систему тел
можно считать замкнутой. При выстреле
снаряд получит импульс и точно такой же по
величине и противоположный по знаку
получит пушка.
36.
• Запишем закон сохранения импульса дляданного случая:
0 m1v1 m2 v2
• откуда скорость отдачи пушки
m1
v2
v1
m2
• Если не закрепить орудие, то оно откатится в
сторону, противоположную движения
снаряда.
37.
• Реактивное движение. Оно такжеобъясняется на основе закона
сохранения импульса. Реактивный
двигатель – это машина, из которой
выбрасываются с большой силой
образующиеся при сгорании топлива
газы. Согласно закону сохранения
импульса, ракета движется в сторону,
обратную направлению газового потока,
причем сумма импульсов ракеты и газов
остается постоянной величиной.


































 physics
physics








