Собственные значения колебаний струны

1.

СОБСТВЕННЫЕ ЗНАЧЕНИЯ КОЛЕБАНИЙ СТРУНЫ
Задачи на собственные значения — это краевые задачи для системы ОДУ, в
которой правые части зависят от одного или нескольких параметров . Значения
этих параметров неизвестны, а решение краевой задачи существует только при
определенных k, которые называются собственными значениями задачи.
Решения, соответствующие этим k, называют собственными функциями
задачи. Правильная постановка таких задач требует формулировки количества
граничных условий, равного сумме числа уравнений и числа собственных
значений.
Задача
Определить собственные значения упругих колебаний струны.
Профиль колебаний струны у(х) описывается дифференциальным
уравнением
(7.1)
где р(х) и q(x) — жесткость и плотность, которые, вообще говоря, могут
меняться вдоль струны. Если струна закреплена на обоих концах, то граничные
условия задаются в виде у(0) = у (1) = 0.
Поскольку решается система двух ОДУ, содержащая одно собственное
значение , то задача требует задания трех (2+1) условий. Производную
решения можно задать произвольно, например, у'(0) = 1.
1

2.

Разрешённое относительно старшей производной, уравнение (7.1) запишется
в виде
(7.2)
Задача на собственные значения может быть решена с использованием
функции sbval (z, x0, x1, D, load, score) — поиск вектора недостающих L
начальных условий для двухточечной краевой задачи для системы N ОДУ:
z — вектор размера Lx1, присваивающий недостающим начальным условиям
(на левой границе интервала) начальные значения;
х0 — левая граница
расчетного интервала; х1 — правая граница расчетного интервала; load(х0, z)
— векторная функция размера Nx1 левых граничных условий, недостающие
начальные условия именуются соответствующими компонентами векторного
аргумента z;
score(x1,у) — векторная функция размера Lx1, выражающая L правых
граничных условий для векторной функции у в точке x1; D(х, у) — векторная
функция, описывающая систему N ОДУ, размера Nx1 и двух аргументов — х и у.
При этом у — это неизвестная векторная функция аргумента х.
Решение задачи о собственных значениях колебаний струны
2

3.

3

4.

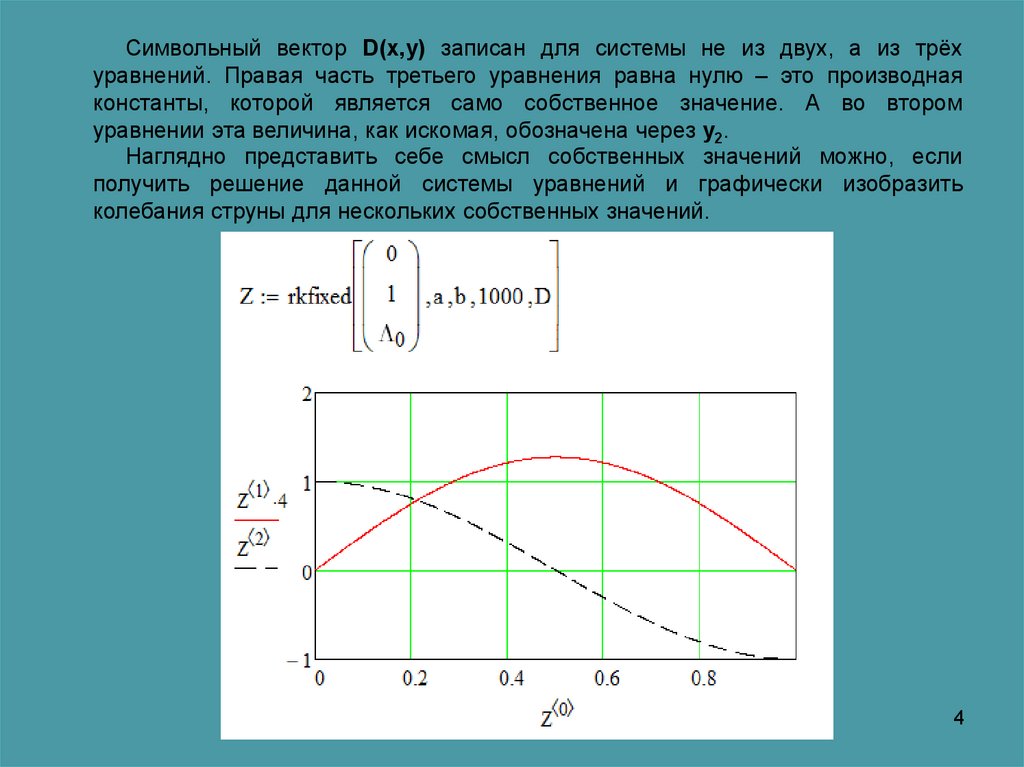
Символьный вектор D(x,y) записан для системы не из двух, а из трёх
уравнений. Правая часть третьего уравнения равна нулю – это производная
константы, которой является само собственное значение. А во втором
уравнении эта величина, как искомая, обозначена через y2.
Наглядно представить себе смысл собственных значений можно, если
получить решение данной системы уравнений и графически изобразить
колебания струны для нескольких собственных значений.
4

5.

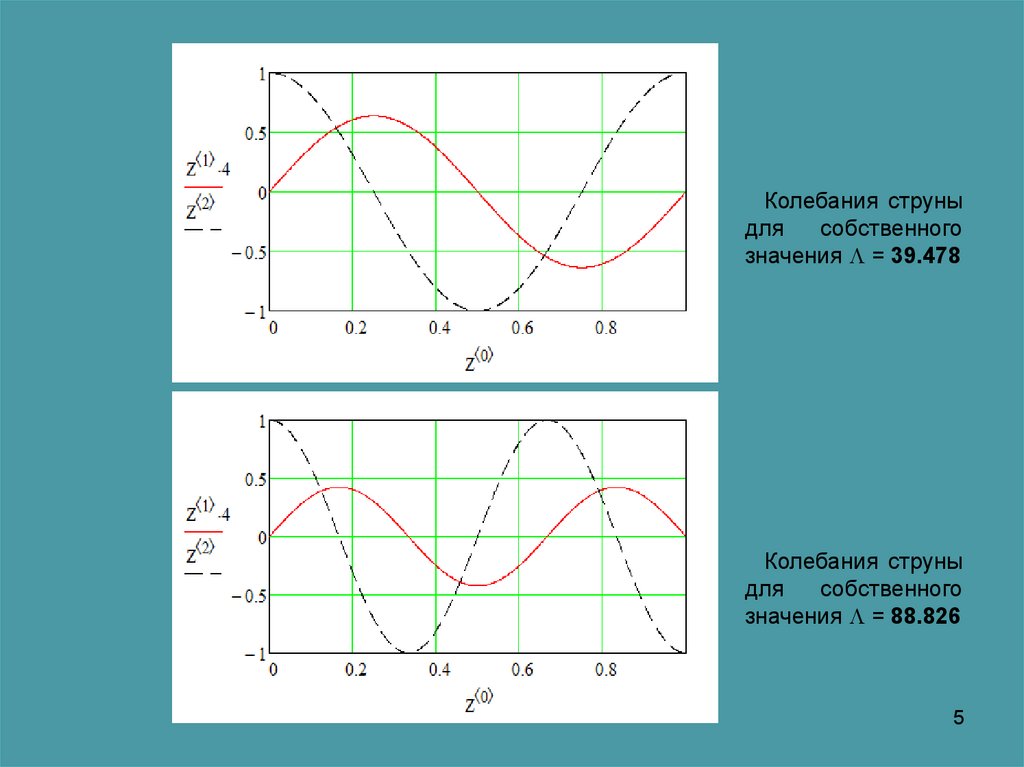
Колебания струны
для
собственного
значения = 39.478
Колебания струны
для
собственного
значения = 88.826
5