Similar presentations:
Основные понятия. Понятие дифференциального уравнения. Лекция 1
1. Лекция 1.
ПланГлава 1. Введение.
§1. Основные понятия.
1. Понятие дифференциального
уравнения.
2. Решение ДУ.
Решение, общее решение, общий
интеграл.
2. 3. Постановка основных задач для ОДУ. Дополнительные условия. 1) задача Коши; 2) краевые задачи; 3) периодическая задача;
3.
Глава 1. Введение.§1. Основные понятия.
Понятие дифференциального уравнения
Определение 1. Дифференциальным уравнением
(ДУ) называют уравнение, в котором
неизвестная функция находится под знаком
производной или дифференциала.
4.
Определение 2. Если неизвестная функциязависит от одной переменной, то такое ДУ
называют обыкновенным дифференциальным
уравнением (ОДУ).
5.
Примеры ОДУ.1)
dy
y
f ( x),
dx
y ( x) ?
f ( x ) C a, b
6.
y( x, C ) F x C7.
2)y ( x) e
y y
x
8.
y( x) Cex
9.
3)dx
x
v,
dt
x t0 x0
10.
x t x0 v t t011.
4)d x
x 2 a, x t0 x0 , x t0 v0
dt
2
12.
a t t0x t x0 v0 t t0
2
2
13.
5)x y R
2
x x t ,
y y t
2
2
14.
xdx ydy 0dx
dy
x y
0
dt
dt
dy
x
dx
y
15.
x R sin t ,y R cos t
16.
.x y
y x.
17.
6)x x 0
2
0
18.
.x t C1 cos 0t C2 sin 0t
x t A sin 0t
19.
x1 x, x2 x.
x1 x2
x2 02 x1.
20.
7)x 2 0 x x 0, 0 0 0
2
0
21.
x t e.
0t
x t Ae
C1 cos t C2 sin t
0t
2
0
sin t
2
0
22.
x1 x, x2 x.
x1 x2
2
x2 2 0 x2 0 x1.
23.
Общий вид ОДУ.t , x t , J x x, x, x,
n
n
, xt
F t, J x 0
n
x, y x , J y y , y , y ,
n
F x, J y 0
n
n
, yx
24.
Определение 3. Порядком ДУ называетсянаивысший порядок входящей в него
производной.
25.
ОДУ 2-го порядкаF x, J y F x y y y 0
2
26.
Определение 4. ОДУ, разрешеннымотносительно старшей производной,
называется ОДУ вида
n
y ( x ) f x, J
n 1
y
27.
Определение 4а ОДУ, разрешенноеотносительно старшей производной, правая
часть которого не содержит явно независимой
переменной, называется автономным.
n
y ( x) f J
n 1
y
28.
Определение 5. Нормальной системой ОДУназывают систему ДУ первого порядка вида
y 1 f1 ( x y1 yn )
y 2 f 2 ( x y1 yn )
y n f n ( x y1 yn )
29.
В векторном виде ее можно записать какy ( x) f x, y
y1 x
y
x
2
y ( x)
,
y
x
n
y1 x
y
x
2
,
y ( x)
y
x
n
30.
f1 ( x y1 yn )f
(
x
y
y
)
2
1
n
f x, y
f n ( x y1 yn )
31.
Примеры ДУ, не являющихся ОДУ.1)
x t x 2t
2)
x t x t 1
3)
t
x t x d
t0
32.
Определение 6 Если в ДУ неизвестная функциязависит от нескольких переменных, то такое
ДУ называют уравнением в частных
производных (УЧП).
33.
Примеры УЧП.1)
A r , grad u r F r , u
u r ,t
2)
div k r , u , t grad u r , t F r , u , t
2
t
u r , t
3)
div k r , u , t grad u r , t F r , u , t
t
4) div k r , u grad u r F r , u
2
5)
f r , v , t
f e
1
f
v
E v , B
0
t
r m
c
v
34.
2. Решение ДУ.Определение 7. Решением ДУ называют
функцию, или совокупность функций,
обращающих ДУ в тождество.
Определение 8. Частное решение ДУ (ЧР) —
конкретная функция, удовлетворяющая ДУ.
35.
Например, частными решениями ОДУy ( x) 4 y ( x) 0
являются функции
y1 sin 2 x,
y2 2 cos 2 x,
y3 3sin 2 x / 4 ,
y4 4 cos 2 x / 6 ,
36.
Множество решений ОДУ n–го порядка зависитот n произвольных постоянных.
Например, множество решений уравнения
y f ( x)
есть
y F ( x) C
37.
Множество решений УЧП 1-го порядкаопределено с точностью до произвольной
функции.
Например, множество решений уравнения
u u
0
x y
есть
u f ( x y)
где f - произвольная дифференцируемая
функция
u ( x y ) , u cos( x y ), u sin e
m
x y
38.
Определение 9. Общим решение ДУ называетсясовокупность всех решений ДУ.
Например, общим решением ОДУ
y ( x) 4 y ( x) 0
является функция
y C1 sin 2 x C2 cos 2 x
или, что то же самое
y A sin 2 x
39.
Определение 10. Процесс нахождения решенияДУ называют интегрированием ОДУ.
Определение 11. Если уравнение
где
C C1 , C2 ,
x, y , C 0
, Cn — вектор произвольных
параметров, определяет все множество
решений соответствующего ДУ, то его
называют общим интегралом данного ДУ, а
полученное из него параметрическое
семейство решений данного ДУ также
называют общим решением.
40.
Замечание. Определенное в 11 общее решениеявляется более узким, по сравнению с 9,
поскольку возможны еще особые решения,
которые не входят в это семейство ни при
значениях параметров.
41.
Пример.dy
y
dx
2
3
Общее решение:
x C
y
3
Особое решение
y 0
3
42.
yC=4
C=0
C= - 4 C= - 8
2
6
10
12
10
8
6
C=8
4
2
y=0
-14
-12
-10
-8
-6
-4
-2
-2
4
8
12
-4
-6
-8
-10
-12
dy
dx
2
3
y ;y
x, C
x
C
3
3
;y 0
14
x
43.
Определение 12. Если для любого решения ОДУy x
функция
F x, J x const x
( p)
то такая функция называется
первым интегралом ОДУ.
В физических задачах первыми интегралами
могут быть энергия, импульс, момент
инерции, масса, заряд и т.д.
44.
УравнениеОбщий интеграл Общее
решение
Частное
решение
Первый
интеграл
F const
y
1.
y f ( x)
2.
x
y
y
3.
y f ( x)dx
C 0
C
y
f d f ( x)dx
x0
2
2
2
2
2
2
y
x
C
y
x
1
y
x
y x C 0
2
2
x C1 cos 0t
x C1 cos 0t
C2 sin 0t 0;
C2 sin 0t ;
x x 0 x
2
0
y f ( x)dx x
x
A sin 0t 0 A sin 0t
x cos 0t
2
2 2
x
0x
45.
Об интегрировании ОДУ в квадратурах.Выражение общего решения или полного
интеграла через элементарные функции и
интегралы от них (берущихся или не
берущихся в элементарных функциях)
называют
интегрированием данного ОДУ в квадратурах.
46.
Интегрирование в квадратурах допускаютлишь уравнения некоторых простейших типов.
Большинство же ОДУ можно решать только
приближенно или исследовать их
качественными методами позволяющими
выяснять свойства решений без явного их
отыскания.
47.
Например, решение уравнения2
y y x
нельзя записать в виде интеграла от элементарной
функции.
48.
Пример. Движение материальной точки массы m поддействием силы
F r Fx x , Fy y , Fz z
которая зависит только от положения точки
(не зависит явно от времени),
а каждая декартова проекция силы зависит только от
соответствующей проекции радиуса– вектора.
Уравнения движения имеют вид
m r F r
49.
или в координатахm x Fx x , m y Fy y , m z Fz z
Общее решение этих уравнений может быть получено
в квадратурах.
Рассмотрим уравнение
m x Fx x
1
x x Fx x x
m
50.
21 d
1
dx
x Fx x
2 dt
m
dt
51.
22
d x Fx x dx
m
52.
22
x Fx x dx C1
m
53.
1/ 22
x Fx x dx C1
m
54.
1/ 2dx
2
Fx x dx C1
dt
m
55.
dtdx
1/ 2
2
Fx x dx C1
m
56.
t C2dx
1/ 2
2
Fx x dx C1
m
57.
Если заданы начальные условияx t0 x0 , x t0 v0
то решение задачи Коши имеет вид:
d
x
t t0
x0
1/ 2
2
2
Fx d v0
mx
0
58.
3. Постановка основных задач для ОДУ.Дополнительные условия.
Наряду с ОДУ для постановки задач
используют начальные (НУ) и граничные
условия (ГУ), количество и вид которых
определяются «физической» постановкой
задачи.
59.
1)Начальная задача (задача Коши)
(Огюстен Луи Коши (1789-1857)французский математик)
n
y ( x ) f x, J
J
n 1
y ,
начальные условия
n 1
y x0 Y
0
или
y ( x0 ) Y y ( x0 ) Y ,
0
0
0
1
,y
n 1
( x0 ) Y
0
n 1
60.
Пример 1. Задача Коши.dy
3
y
x 3
dx
y
3
y (0) 1
2
3
Решение задачи существует и единственно!
61.
Пример 2. Задача Коши.dy
3
y
x
dx
y , y 0
3
y (0) 0
2
3
Решение задачи существует, но не единственно!
62.
2)Краевая задача (обычно 2-х точечная):
y ( x) f x, y, y , x a, b
граничные условия первого рода (задача Дирихле):
y(a) ya ,
y(b) yb
граничные условия второго рода (задача Неймана):
y (a) ya ,
y (b) yb
граничные условия третьего рода:
y (a) y a ya ,
y (b) y(b) yb
периодические граничные условия:
y ( a) y b a ,
y (a) y b
63.
Пример 1. Краевая задача.d y
1, x 0,1
x
2
dx
y 1 x
2
y (0) 0, y (1) 0
2
Решение задачи существует и единственно!
64.
Пример 2. Краевая задача.d y
1, x 0,1
2
dx
y (0) 0, y (1) 0
2
Решение задачи не существует!
65.
Пример 3. Краевая задача.d y
0, x 0,1
2
dx
y C
y (0) 0, y (1) 0
2
Задача имеет бесконечное множество решений!
66.
3) Периодическая задача.В общем случае задача о периодических решениях —
это задача о нахождении T-периодического решения
уравнения
x f t, x
правой частью:
, с T-периодической по t
f t, x f t T , x





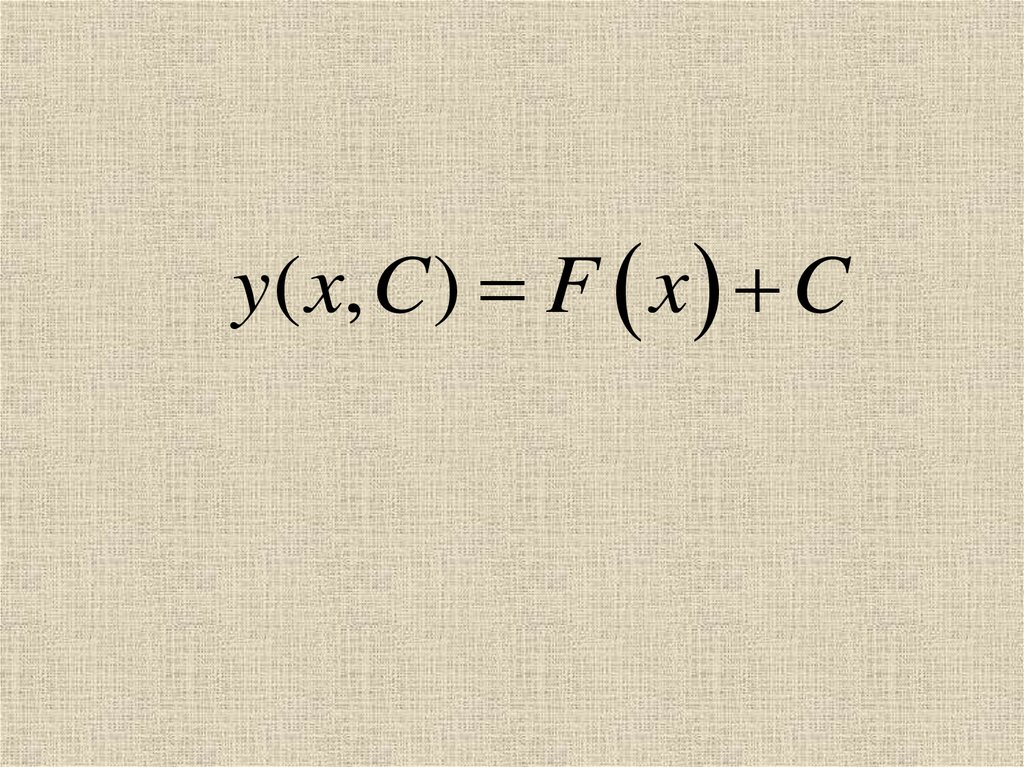
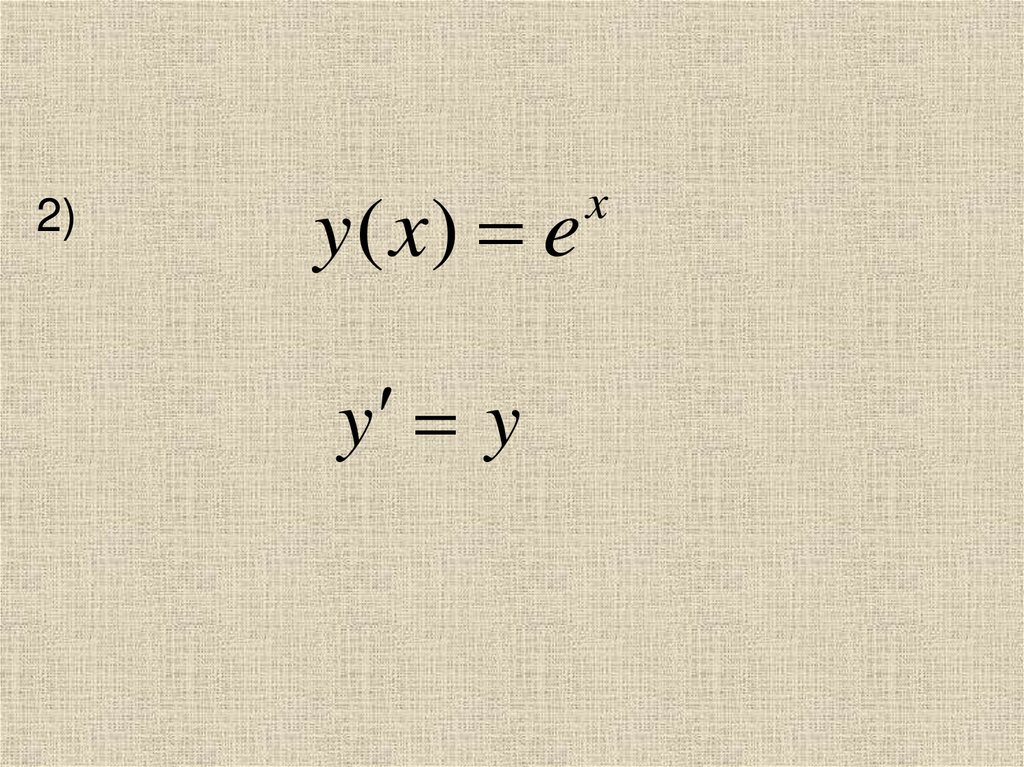
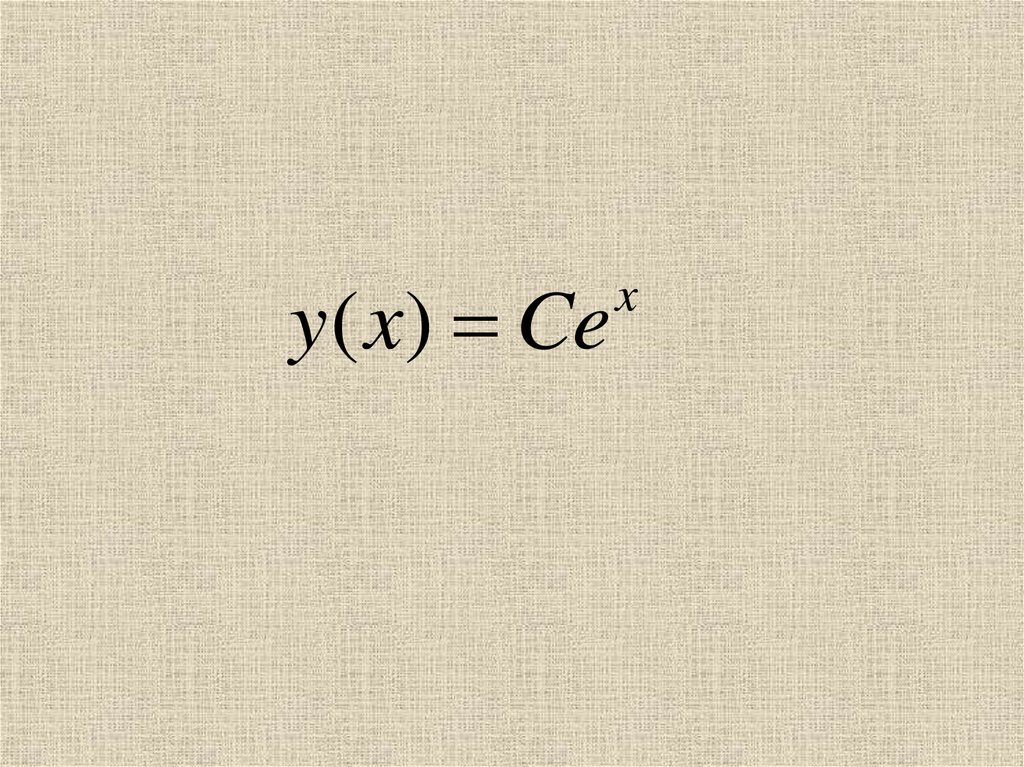


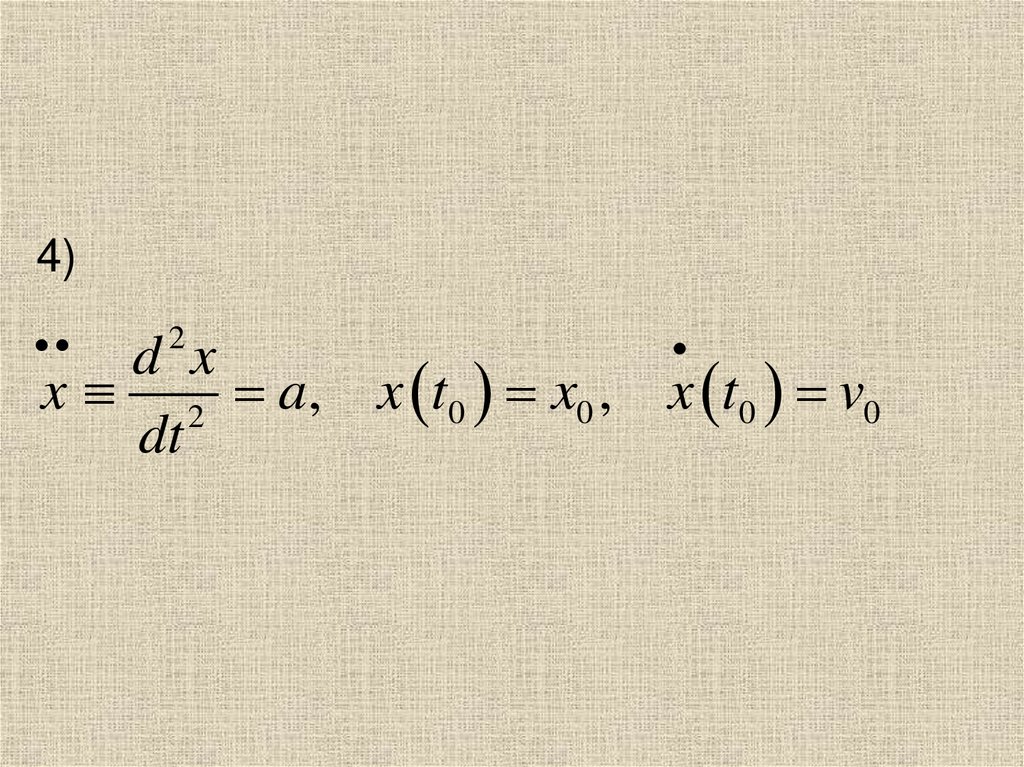






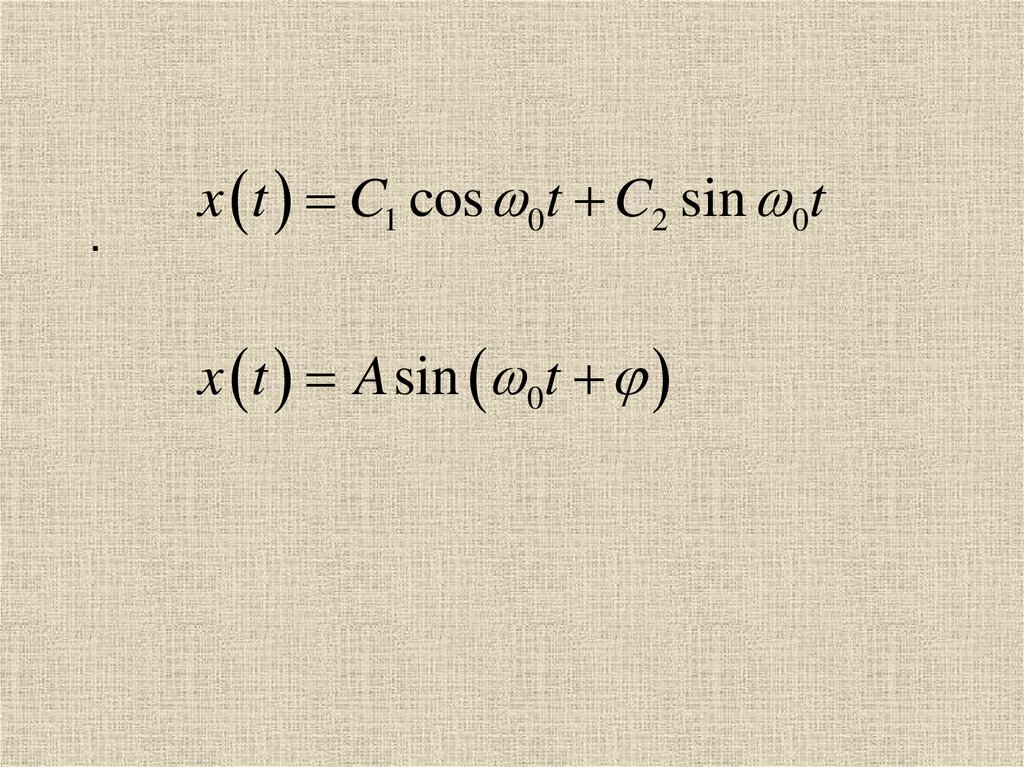

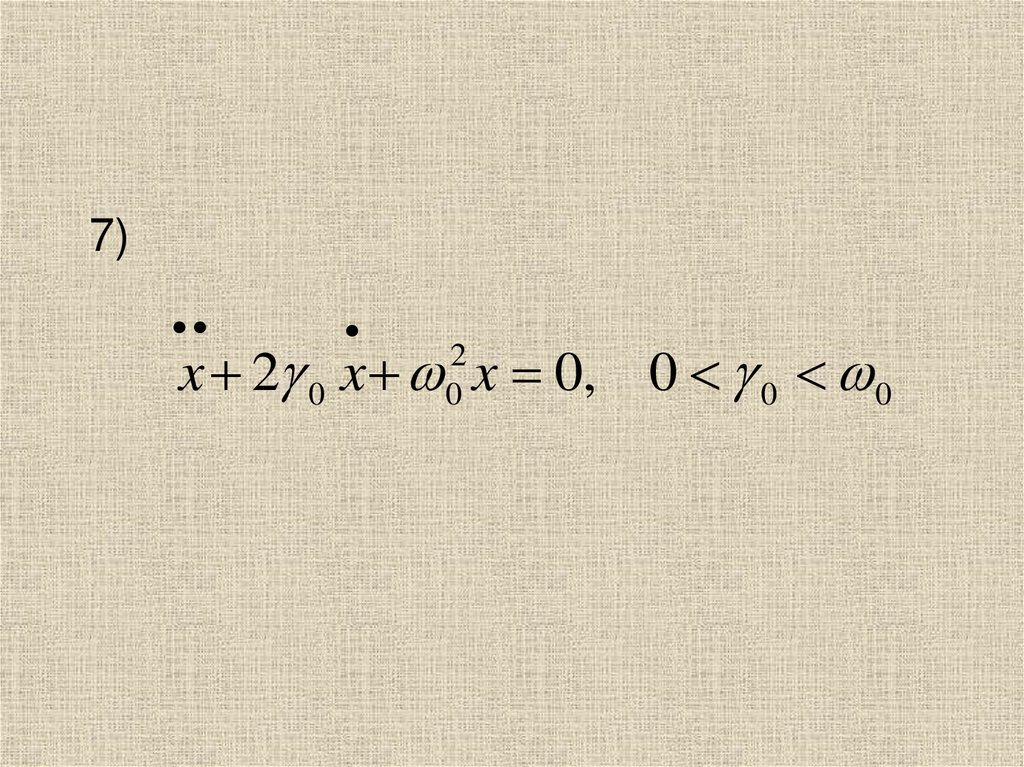
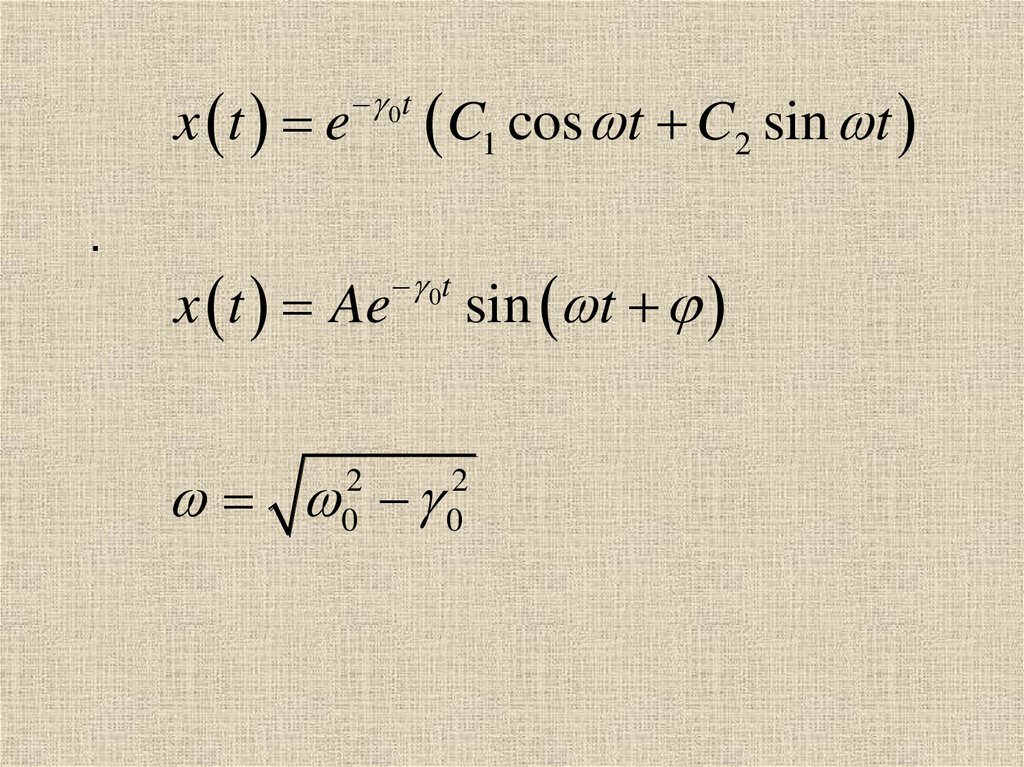
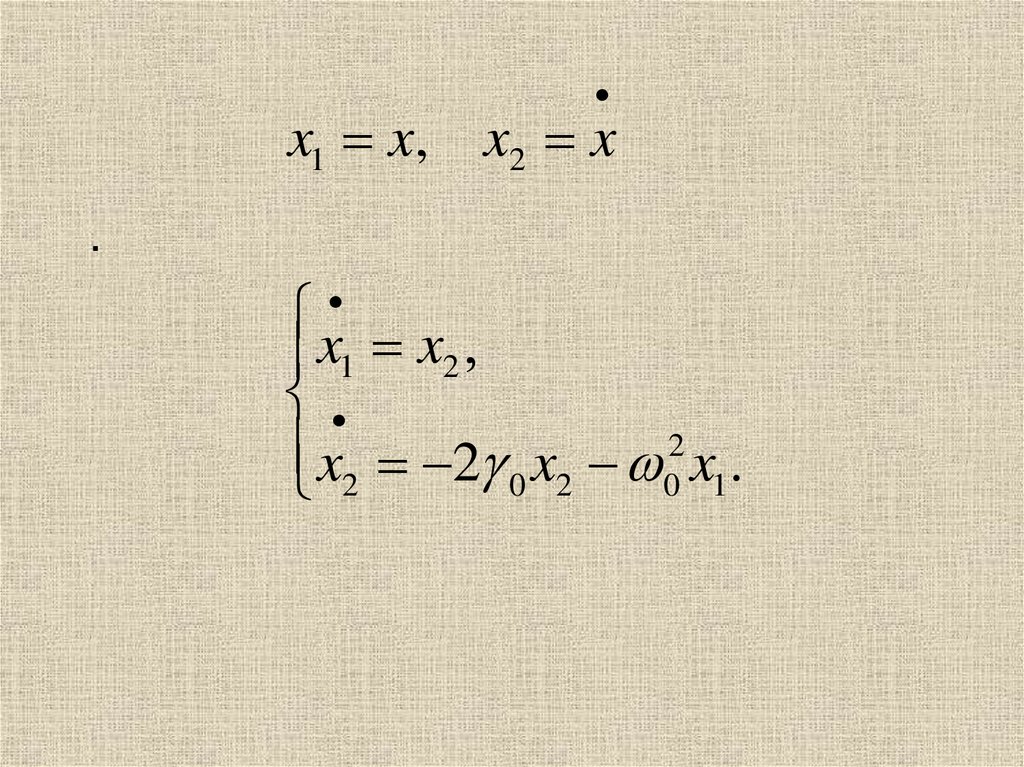
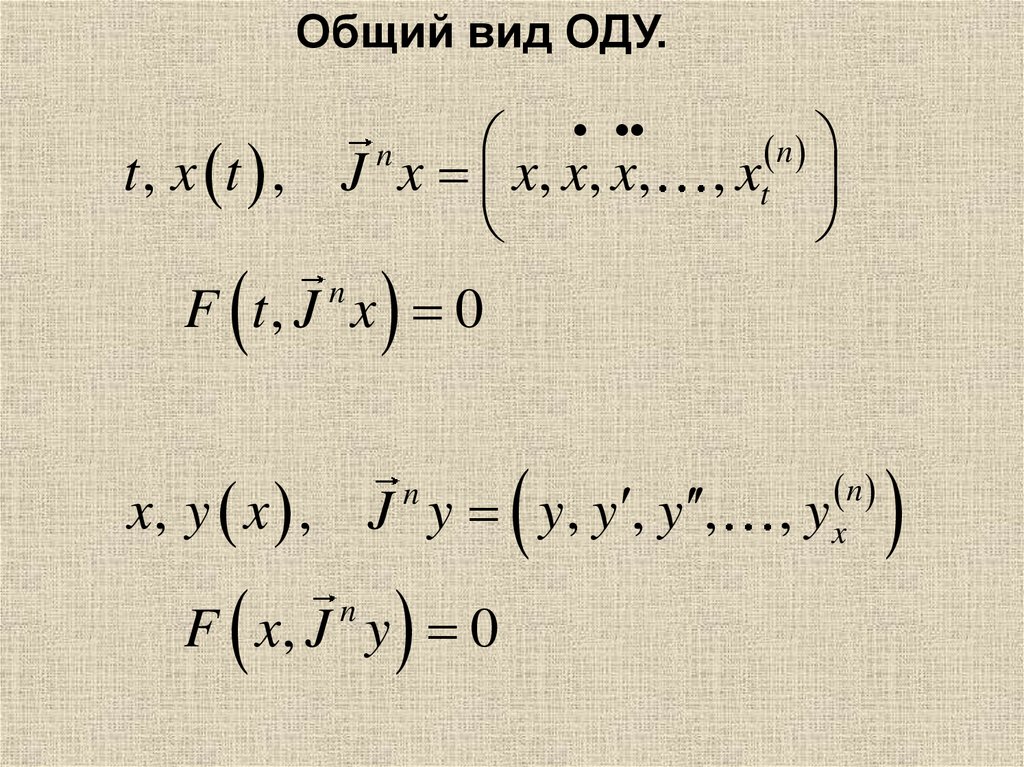







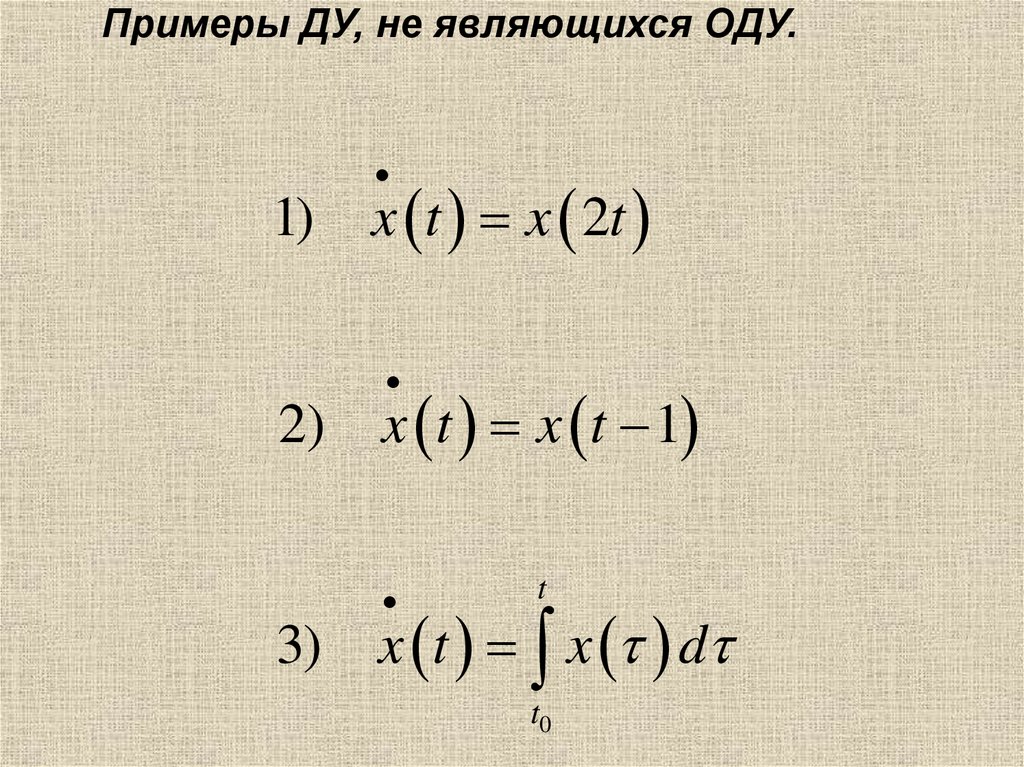





















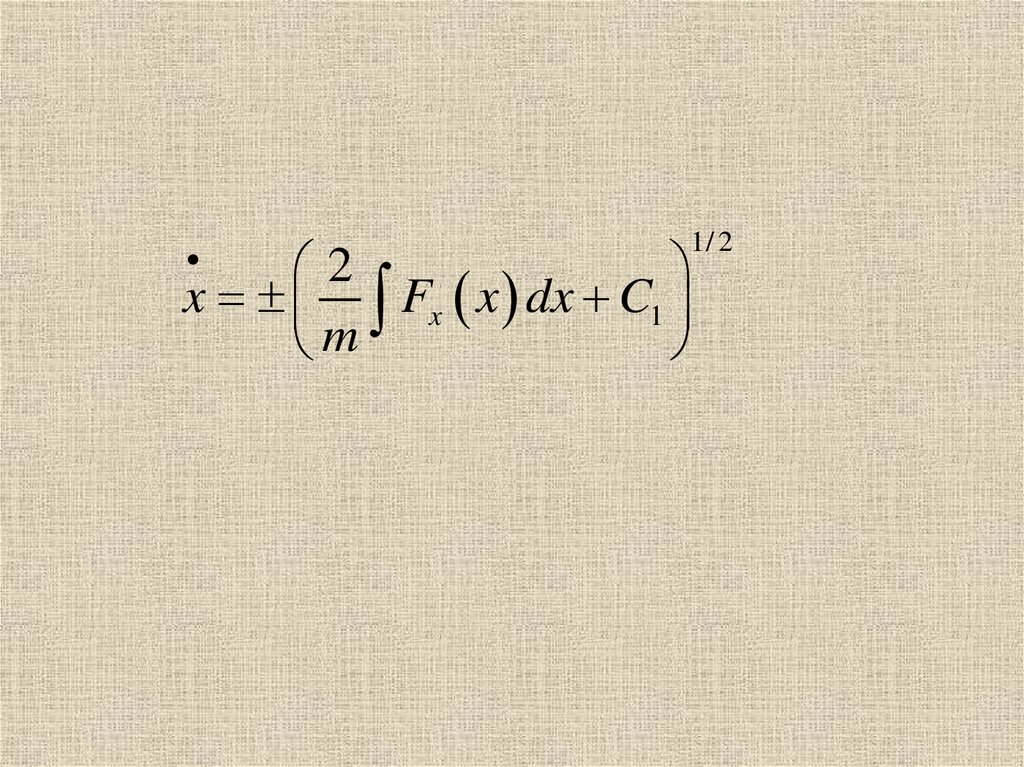


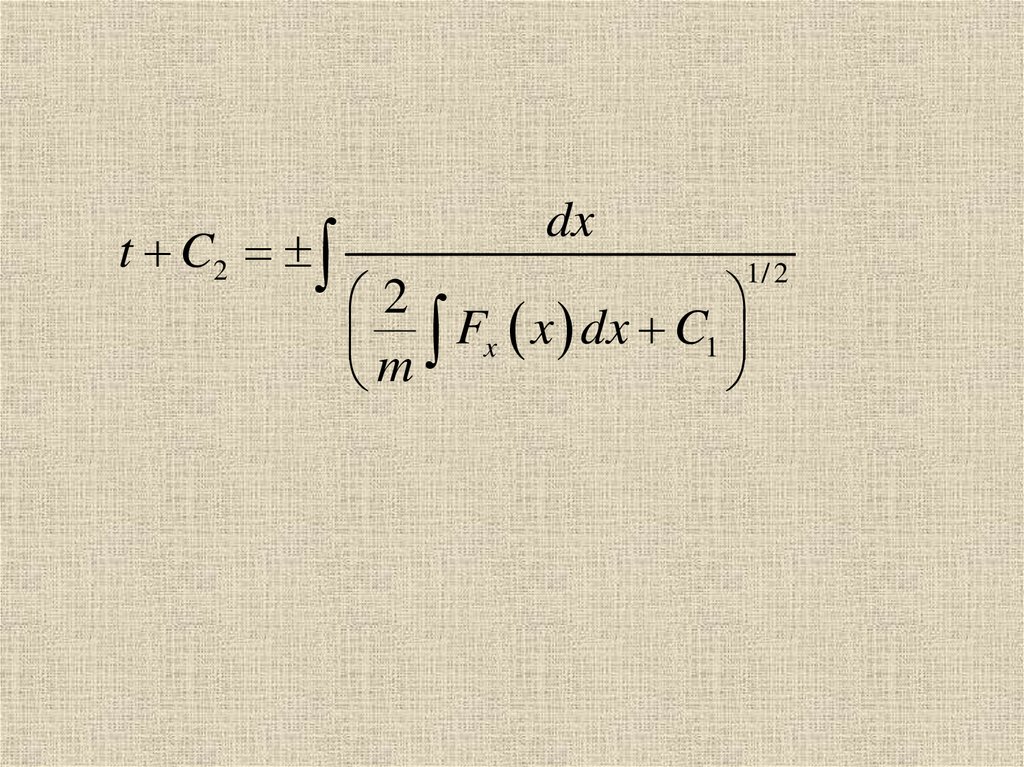










 mathematics
mathematics








