лк 3 -6

1. Тема 1. ОСНОВНЫЕ УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ Лекция №3-6 Волновые уравнения

1. Волновые уравнения произвольной
электромагнитной системы источников.
2. Векторный и скалярный потенциалы
для мгновенных значений поля
3. Калибровка потенциалов
1

2. 1 Волновые уравнения произвольной электромагнитной системы источников.

D
Преобразуем первое уравнение Максвелла rot H j t ,
используя закон Ома j э E и материальное уравнение
D 0 E .
э
Поскольку параметры среды не зависят от времени, то получаем
э
D
E
rot H j
E 0
t
t
Применим операцию rot к правой и левой частям:
rotrot H rot E 0
(rot E )
t
B
H
Учтем из второго уравнения Максвелла rot E 0
,
t
t
получаем
H
2 H
rotrot H 0
0 0 2
t
t
2

3.

Учтем
rot rot H grad div H H и получим
2
2
(1)
H
H
2
H a a 2 a
0
t
t
Аналогичным образом преобразуется второе уравнение к виду
2
E
E
2
E a a 2 a
0
t
t
(2)
Уравнения (1) и (2) называют векторными обобщенными
однородными волновыми уравнениями.
3

4.

Разновидности волновых уравнений
1. Векторные однородные волновые уравнения для идеального
диэлектрика ( 0 )
2 E
2 H
2
2
E a a 2 0
H a a 2 0
t
t
или
H
где
c
2
2 H
c
t
2
1
0 0
2
0
3 108
E
2
2 E
c
2
t
2
0
[м/с] - скорость света.
2. Векторные неоднородные уравнения (уравнения Даламбера)
H
2
2 H
c
2
t
2
rot j
В среде без потерь ( 0 )
ст
H
H 2 2 rot j
c t
2
2
2 E
j
E 2 2
grad 0
0
t
c t
2
1
ст
E 1
j
ст
E 2 2
grad 0
0
t
c t
2
2
4

5.

В среде без потерь ( 0 )
2 H
2 H
c
2
t
2
rot j
ст
E
2
E
2
c
2
t
2
1
0
ст
grad
ст
j
0
t
3. Уравнения Пуассона (отсутствует временная зависимость).
Пренебрежение токами смещения.
H rot j
2
ст
2 E ( 0 ) 1 grad ст
Основные понятия векторной алгебры: 2 a grad div a rot rot a
div grad 2
Лапласиан в декартовой системе координат:
2
2
2
2
- для скаляра
x 2
- для вектора
y 2
z 2
2 a ix 2 a x i y 2 a y iz 2 a z
5

6.

Физическая трактовка 1 и 2 уравнений Максвелла : изменение во
времени электрического поля приводит к изменению магнитного
поля и наоборот.
Волновой процесс – колебательное движение непрерывной среды.
Решение уравнений Максвелла – две волновые функции (волны):
расходящаяся и сходящаяся волны.
Волнами переносится ЭМ энергия из объема, где действуют
переменные сторонние токи, в окружающее этот объем
пространство, где этих токов нет.
Процесс распространения в пространстве электромагнитных волн с
конечной скоростью и утративших связь со своими источниками
(переменными зарядами и токами), называется излучением
электромагнитных волн.
9

7.

Решение задачи об излучении заключается в определении в любой
точке пространства структуры ЭМП, возбуждаемого сторонними
токами.
С математической точки зрения задачи о возбуждении ЭМВ
заданными источниками сводятся к решению системы
неоднородных уравнений Максвелла:
Для произвольных сигналов
Для гармонических сигналов
э. ст.
E
rot H E a
j
t
м. ст.
H
rot E a
j
t
a div E э.ст
a div H
м.ст
rot H i a E j
ст.э
rot E i a H j
ст. м
a div E э.ст
a div H м.ст
Для получения единственного решения системы должны быть
дополнены 1) граничными условиями; 2) условиями излучения.
10

8.

2 Векторный и скалярный потенциалы
для мгновенных значений поля
Решение неоднородных уравнений является неточным, т.к.
сторонние источники известны приближенно: данные берутся
из опытов или предположений.
Выход из положения – введение электродинамических
э
м
потенциалов: векторного ( A , A ) и скалярного ( u э , u м ).
Для каждого типа источника выбирается один вид потенциалов.
Вводятся с помощью 4 уравнения Максвелла и закона непрерывного
тока:
э
э
A
A
э
э
E grad u
rot E
0
a H rot A
t
t
э
Знак «минус» перед grad u введен для совпадения в случае
электростатического поля функция с обычным выражением для
электростатического потенциала.
Электродинамика и РРВ.Сем.1. Лекция 4(4).
11

9.

Подстановка выражений для потенциалов в 1 уравнение Максвелла
и учет материальных уравнений позволяет записать:
э
э
э
2
э
э ст
u
A
A
1
э
( 0 ) rot rot A j
0 grad
grad
u
t
t
t2
Введение потенциалов было произвольным. Для устранения
неоднозначности вводится условие калибровки. Классическое
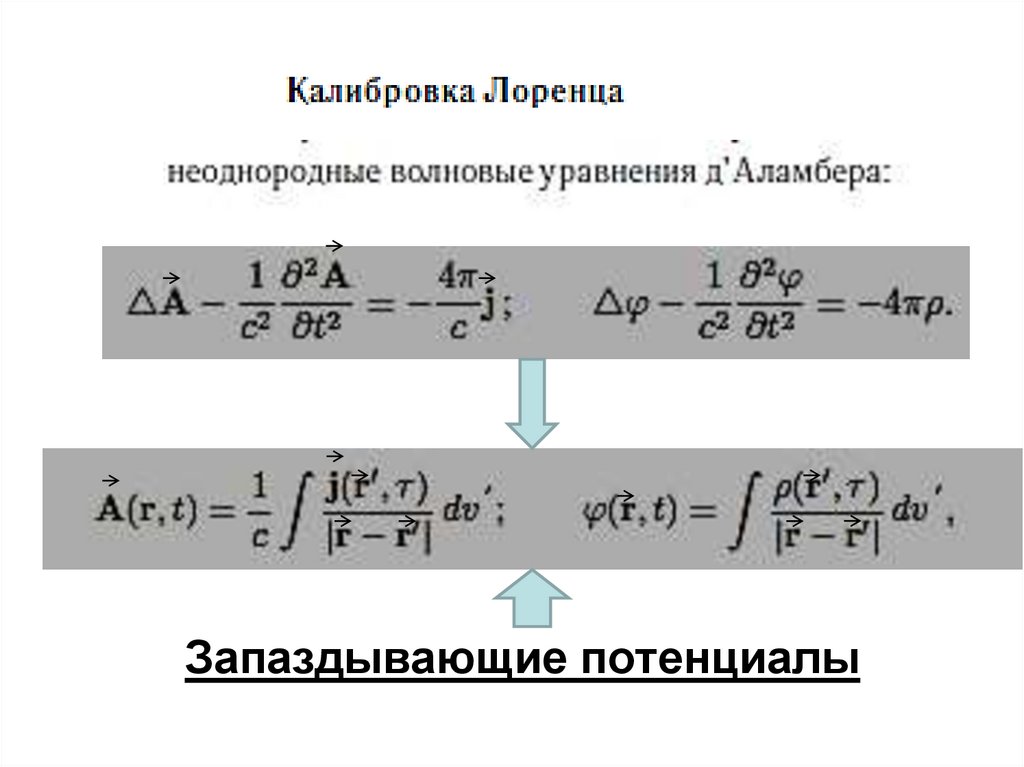
условие – калибровка Лоренца:
э
u э
div A 2
uэ 0
c
t
С учетом калибровки
волновые
уравнения принимают вид:
э
э
э
A
2
2 A
c2
э ст
A
0 j
2
t
t
2u э
э
A
э ст
2 э
u 2
2
t
0
c t
Достоинство: в правые части входят сторонние источники
тока, а не их производные.
12

10.

Введение электродинамических потенциалов электрического типа:
E
1
0
rot A
м
м
м
A
H grad u 0
A
t
м
м
u
Условие калибровки:
div A 0
0
t
Получаемые волновые уравнения:
м
м
м
м
A
A
A 0 0
0
j
2
t
t
2
м
2
2 м
м
м
u
u
2u м
2
t
t
0
13

11.

Запаздывающие потенциалы

12.

Кулоновская калибровка
Калибровка
Кулона

13.

14.

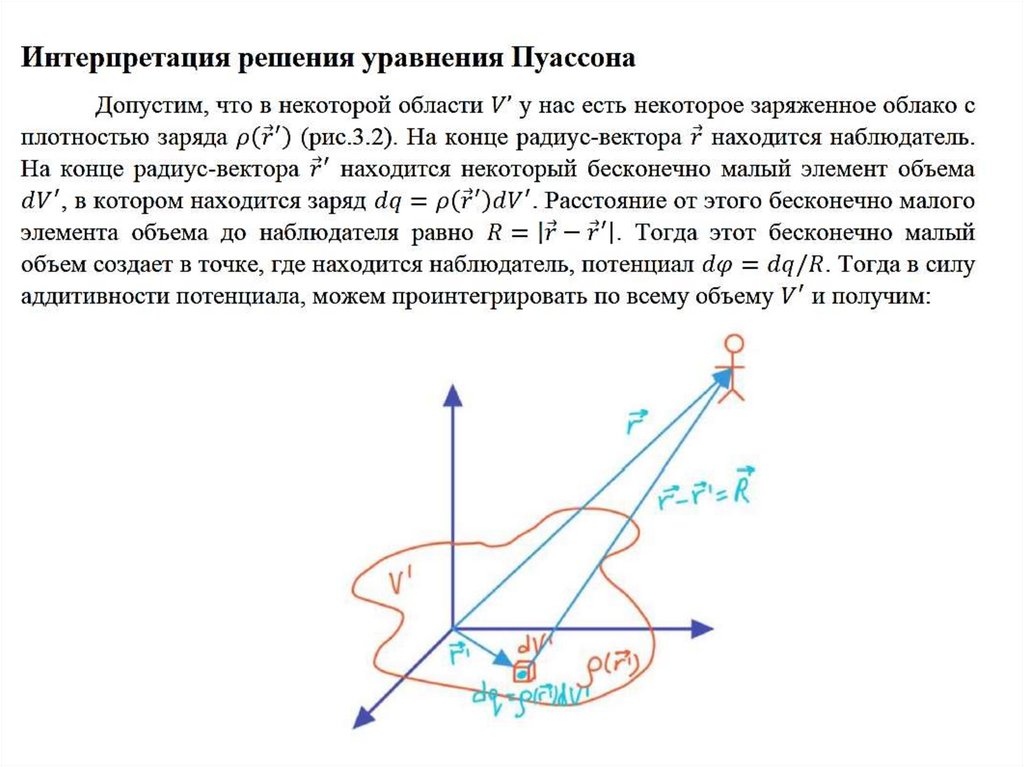
Электростатика. Уравнение
Пуассона

15. Кулоновская калибровка

В электростатике

16.

Уравнение Пуассона, требует
граничных условий!

17. Электростатика. Уравнение Пуассона

18. В электростатике

Тогда: