Similar presentations:
Экстремальные кривые в задаче Эйлера об эластиках
1. Экстремальные кривые в задаче Эйлера об эластиках
Ардентов Андрей.Исследовательский центр
процессов управления ИПС РАН
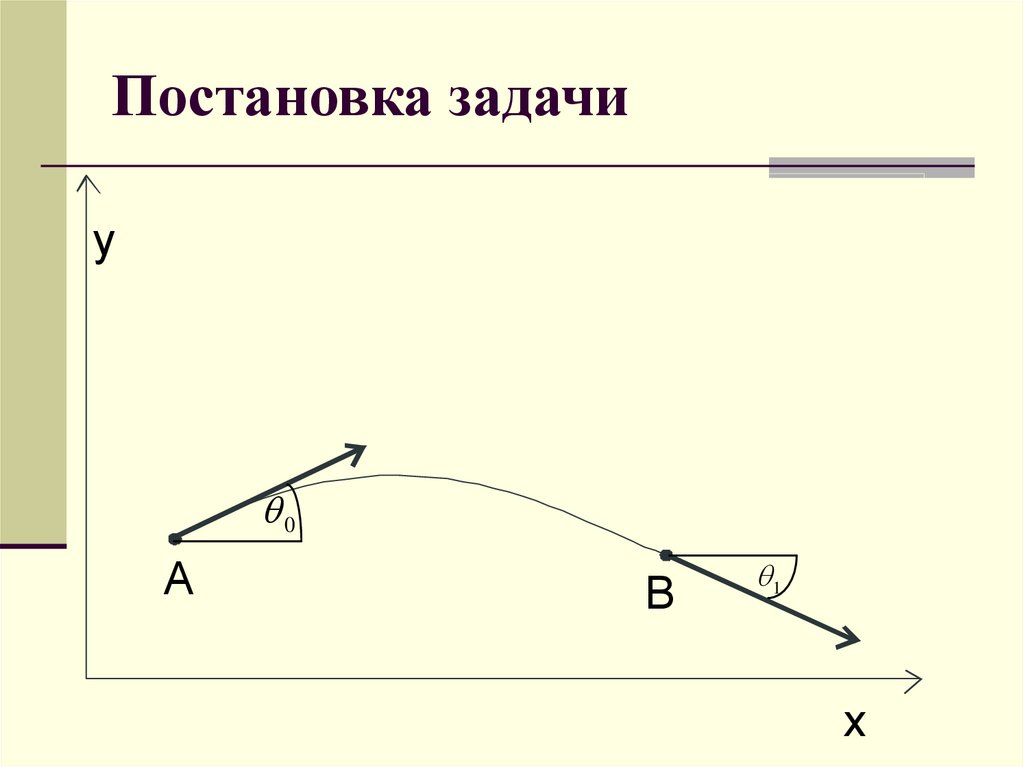
2. Постановка задачи
y0
A
B
1
x
3. Постановка задачи
yk
dt
min
2
x
(0,0)
(x1,y1)
1
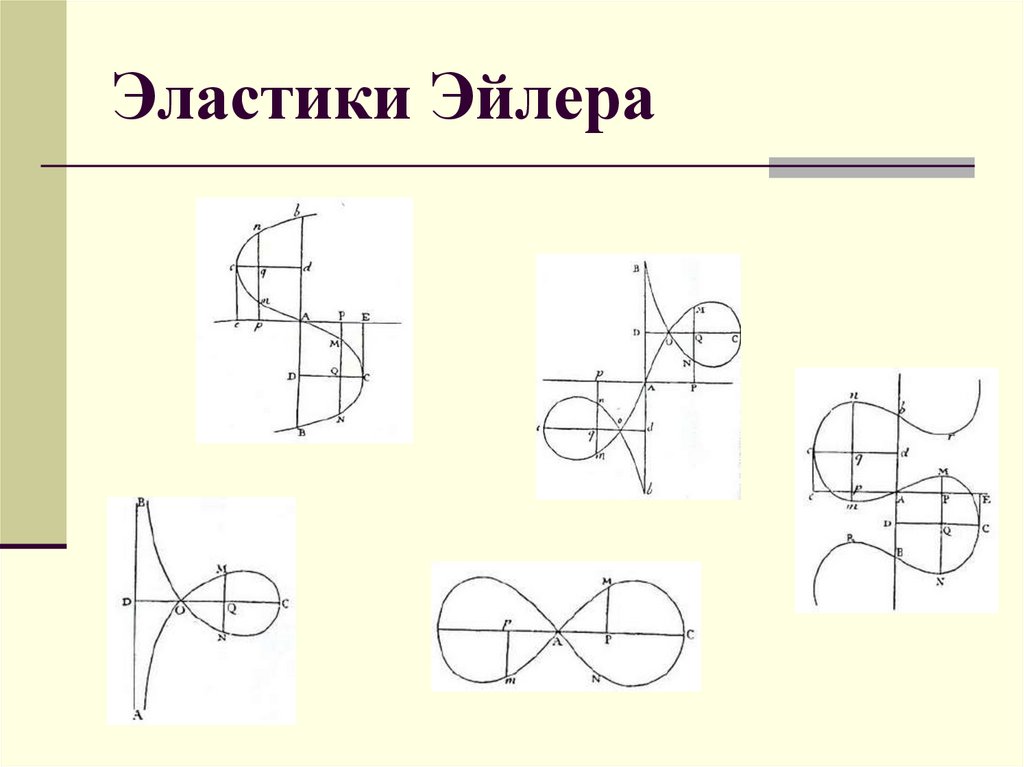
4. Эластики Эйлера
5. Задача оптимального управления
x cos ,y
sin
,
u
t1
E 1 k 2 ( t )dt min ,
2 0
x(0) 0, x( t 1 ) x1
y(0) 0, y( t 1 ) y1
(0) 0, ( t 1 ) 1
k ( t ) x ( t )
6. Принцип Максимума Понтрягина
3ψ (ψ , ψ , ψ , ψ ), Η(ψ, x, u) ψ f (x, u)
a a
0 1 2 3
a 0
û(t), x̂(t) оптимальный процесс ψ(t) 0, т. ч.:
ψ 0
0
3
f
ψ ψ (t) a (x̂(t),û(t)),
i 1,2,3
i
a x
a 0
i
max Η(ψ(t), x̂(t), u) Η(ψ(t), x̂(t), û(t)); ψ 0.
0
u U
7. Гамильтонова система принципа максимума
u21 cos 2 sin 3 u,
0
2
1 2 0,
sin cos .
1
2
3
0 0
3 0
const .
0 1 3 u c1 sin c 2 cos
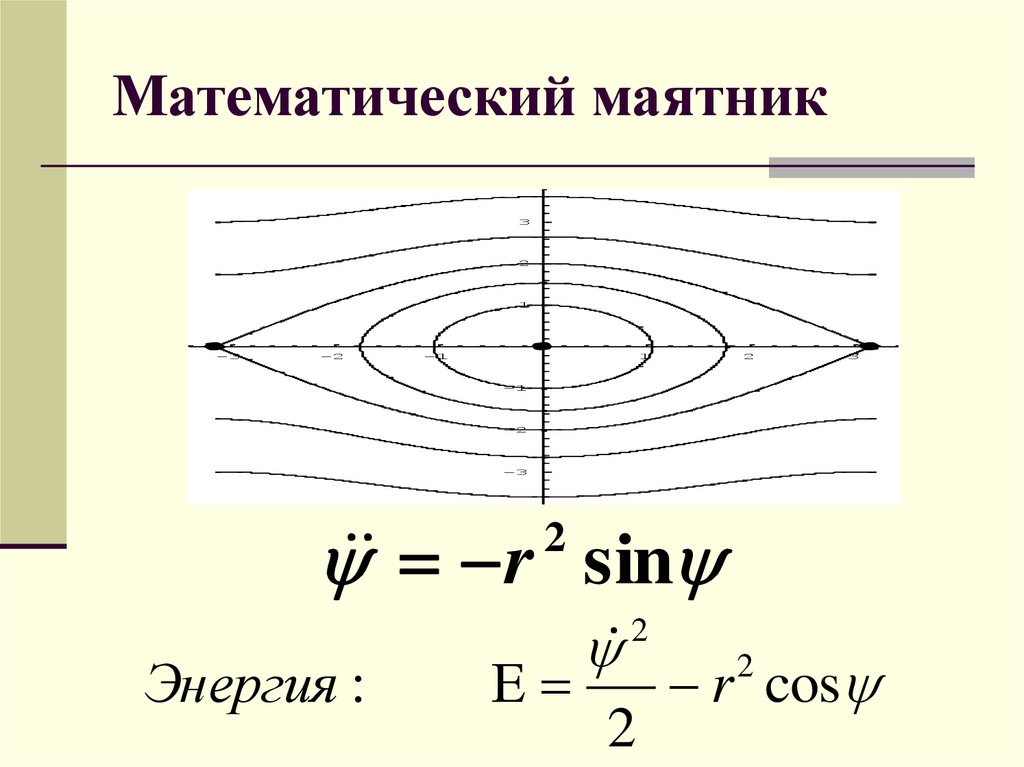
8. Математический маятник
32
1
-3
-2
-1
1
2
3
-1
-2
-3
r sin
2
Энергия :
2
2
r cos
2
9. Эллиптические функции Якоби
Эллиптические интегралы I и II рода:F( , k)
dt
E ( , k ) 1 k 2 sin 2 t dt.
2
2
1
k
sin
t
0
Полные эллиптические интегралы :
0
K ( k ) F ( , k ),
E (k ) E ( , k )
2
2
Определение ээллиптичских функций Якоби :
am u u F( ,k),
sn u sin am u,
cn u cos am u,
dn u 1 k 2 sn 2u ,
(u) E(am u,k).
10. Эллиптические координаты в фазовой плоскости маятника
sin 2 k sncos dn
2
c
k cn
2
1
k
2
k 0
1
11. Параметризация эллиптическими функциями
θ(t) 2 arcsin (k (dn(b 0 )sn(b 0 r t)-sn(b 0 )dn(b 0 +r t))),2
2
2
2
2
x(t)
(dn
(b
)-(k
sn(b
))
)(Ε(Ε
+r
t)-Εr
))-(dn
(b
)-(k
sn(b
))
)t0
0
0
0
0
0
r
( 2k) 2
sn(b0 )dn(b0 ) (cn(b 0 +r t)-cn(b0 )),
r
y(t) 2 k(sn(b 0 )dn(b0 )t- 2 sn(b0 )dn(b0 ) (Ε ( 0 +r t)-Εr 0 ))
r
1
- (dn 2 (b0 )-(k sn(b 0 )) 2 )(cn(b 0 +r t)-cn(b0 ))).
r
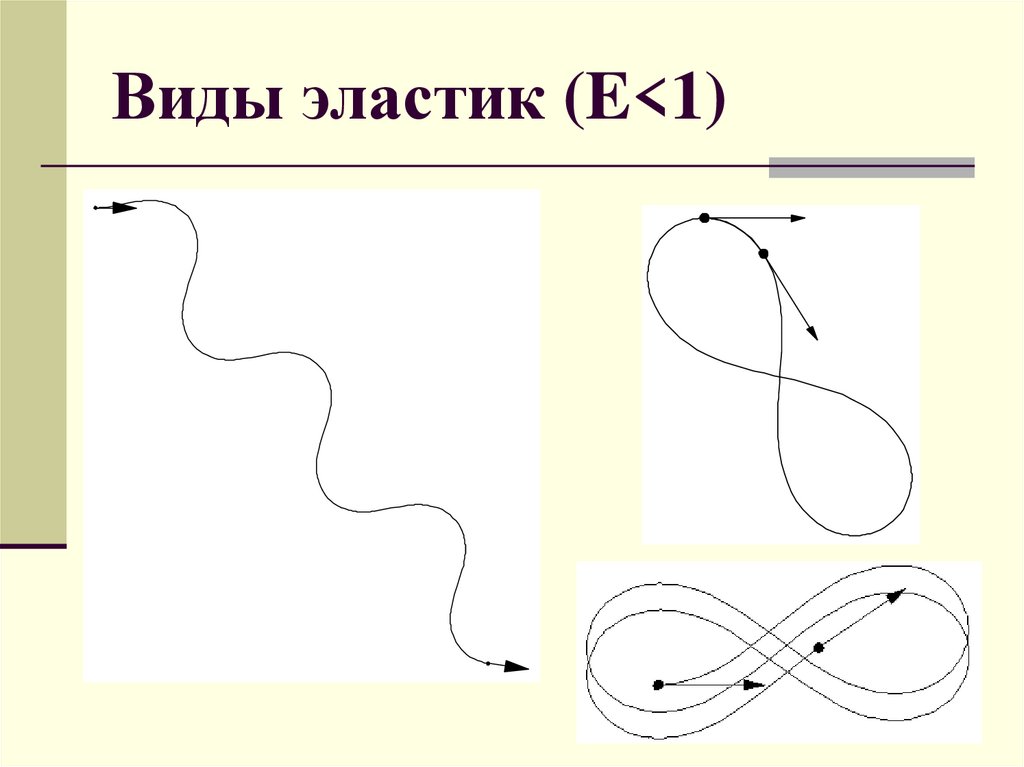
12. Виды эластик (E<1)
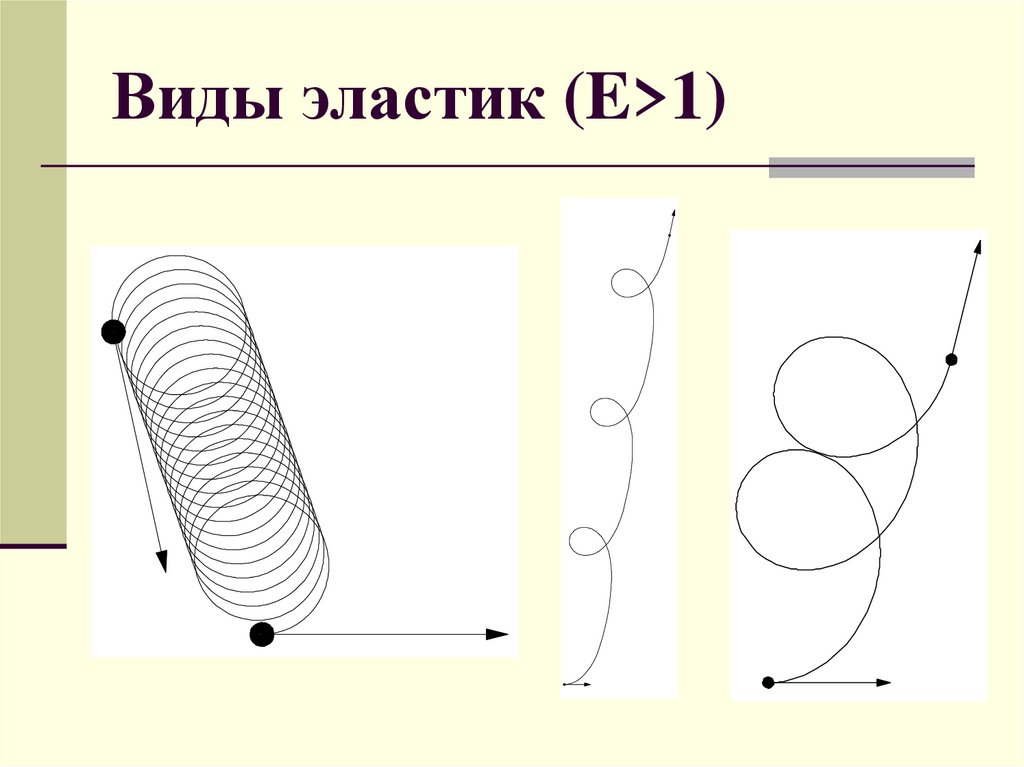
Виды эластик (E<1)13. Виды эластик (E>1)
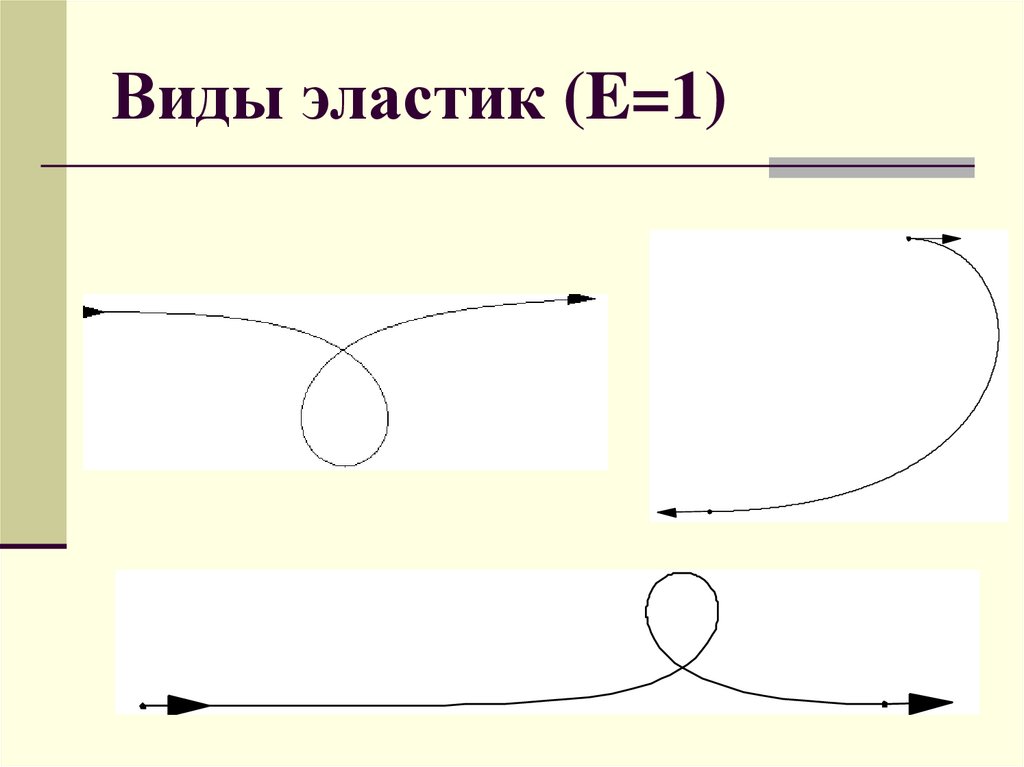
Виды эластик (E>1)14. Виды эластик (E=1)
15. Нахождение кривых по заданным граничным условиям
1 (b0 , k , r )x 1 x(b0 , k , r )
y y(b , k , r )
0
1
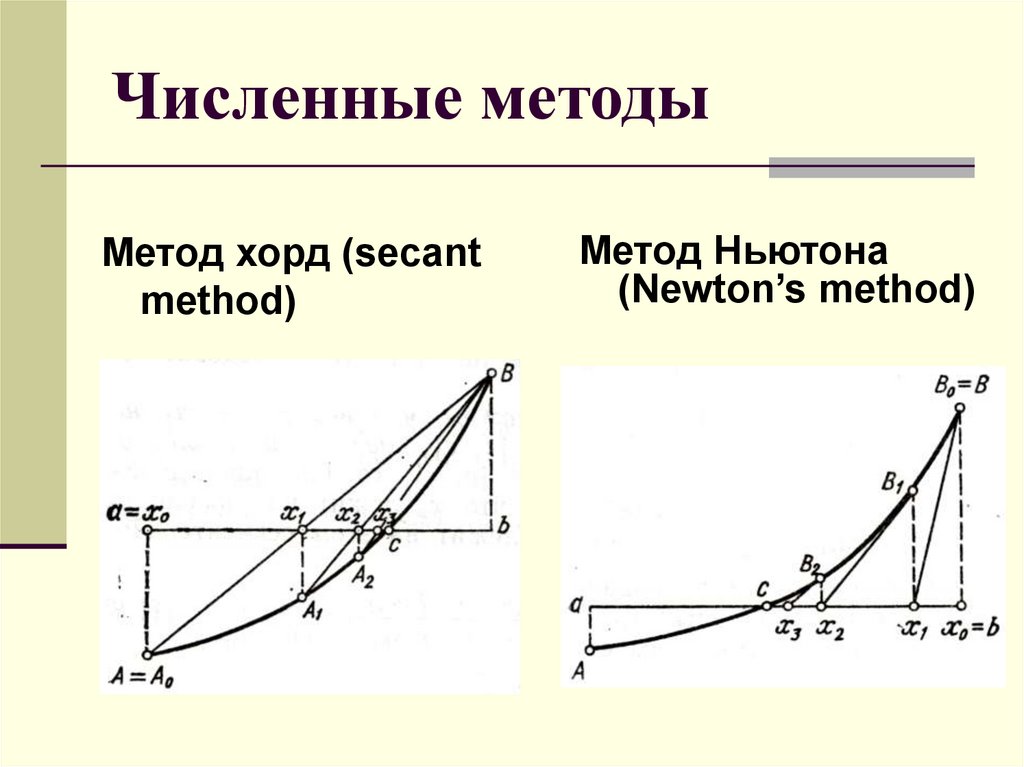
16. Численные методы
Метод хорд (secantmethod)
Метод Ньютона
(Newton’s method)
17. Программа на Mathematica
x1Function k, u, v ,
1
1
2
k
k2 Sin u 2 Sin v 2 3
1
2
1 k Sin u
2
4 k Sin u
EllipticF u, k2
2 1
2
k Cos u Sin u
1
2
2
k
2
1 k2 Sin u 2 Sin v
Cos u
1 k2 Sin v 2
1 k2 Sin u 2
1 k2 Sin v 2
2
EllipticF u, k2
Sin v
1 k2 Sin u 2 Sin v
k Cos u Cos v Sin u Sin v
1
2
3 Cos 2 u
1 k2 Sin u 2 Sin v
Sin v
2
2
1 k2 Sin u 2 Sin v
Cos u
2
1 k Sin u
2
2
2
1 k Sin u
2
Sin v
2
2
Sin v
2
2
Cos v Sin u
1 k2 Sin v 2
2
k Cos u Cos v Sin u Sin v
1 k2 Sin u 2 Sin v
4 k Cos u Cos v Sin u
EllipticE u, k
1 k2 Sin v 2
Cos v Sin u
1 k2 Sin v 2
2
k
1 Cos v
1 k2 Sin u 2
2
Sin u
2
1 k2 Sin v 2
1
1
2
2
k
3 Cos 2 u
;
y1
Function k, u, v ,
1
1
k2 Sin u 2 Sin v 2 3
2k
1 k Sin u
2
2
Sin v
2
1 k2 Sin u 2 Sin v
Cos u
Cos v Sin u
1 k2 Sin v 2
2
k Cos u Cos v Sin u Sin v
1
1 k2 Sin u 2
1 k2 Sin v 2
Sin u
1 k2 Sin u 2 Sin v
1 k2 Sin v 2
EllipticF u, k2
1 2
1 2
2
2
2
2
2
2
1
k 3 Cos 2 u Sin v
4 k Cos u Cos v Sin u
1 k2 Sin u 2 Sin v
1 k2 Sin v 2 k 1 Cos v
Sin u
1
k 3 Cos 2 u Sin v
2
2
1
2
2 Cos u
1 k2 Sin u 2 Sin v Cos v Sin u
1 k2 Sin v 2 k Cos u Cos v Sin u Sin v
1 k2 Sin u 2 1 k2 Sin v 2
EllipticF u, k2
2
k Cos u Sin u
2
EllipticE u, k
2 k Cos v Sin u
1 k2 Sin u 2
1 k2 Sin u 2 Sin v
sinThetaDT1
Function k, u, v ,
cosThetaDT1
Function k, u, v ,
1
2
k2 Sin u 2 Sin v 2
2
1 k Sin u
2
Sin v
2
;
;
8 6 k2 6 k2 Cos 2 u
k2 Cos 2 u v
2 k2 Cos 2 v
k2 Cos 2 u v
8 2 k2 2 k2 Cos 2 u
k2 Cos 2 u v
2 k2 Cos 2 v
k2 Cos 2 u v
;
2
Sin v
2
18. Результаты тестирования программы на skif.botik.ru
Количество тестов - 2500.Потраченное время - 70:49:12.
Время на тест в среднем - 00:01:41
Среднее кол-во попыток - 17.8732.
Макс. время на тест - 23:45:37.
Макс. кол-во попыток - 17585.
19. Результаты
• Благодаря эллиптическим координатамв фазовой плоскости математического
маятника, получена новая
параметризация эйлеровых эластик с
помощью эллиптических функций
Якоби.
• Написана программа в системе
Mathematica для поиска оптимальных
эластик по заданным граничным
условиям.












 mathematics
mathematics








