Similar presentations:
Алгоритмы автоматического выбора шага
1.
Алгоритмыавтоматического выбора шага
2.
До сих пор мы рассматривалиодношаговые численные методы
с постоянным шагом интегрирования.
Такие методы неэффективны при решении задач
с внутренними пограничными слоями –
областями резкого изменения фазовых переменных.
Очевидно, что для аппроксимации точного решения
в таких областях требуется значительно меньший шаг,
чем в остальной области. При постоянном шаге
избыточное число расчетных точек окажется в
области гладкого поведения решения, где они не нужны.
3.
В качестве примера рассмотрим решение задачио движении материальной точки единичной массы
в плоскости Лапласа (x, y) в центральном поле
притягивающего ньютоновского потенциала u = - r -1.
dvx/dt = - xr -3, dvy/dt = - yr -3,
dx/dt = vx, dy/dt = vy,
при начальных условиях х0 = 1.0, y0 = 1.0, vx,0 = 0.1, vy,0 = 0.2.
Силовой центр расположен в начале координат (0, 0).
В этом случае орбита является вытянутым эллипсом,
в одном из фокусов которого находится силовой центр.
В промежутке времени, когда точка находится в окрестности
силового центра, фазовые переменные резко изменяют свои
значения во времени.
Наблюдается характерный пограничный слой,
вне которого зависимости фазовых переменных от времени
являются достаточно гладкими.
Рассмотрим графики решения поставленной задачи.
4.
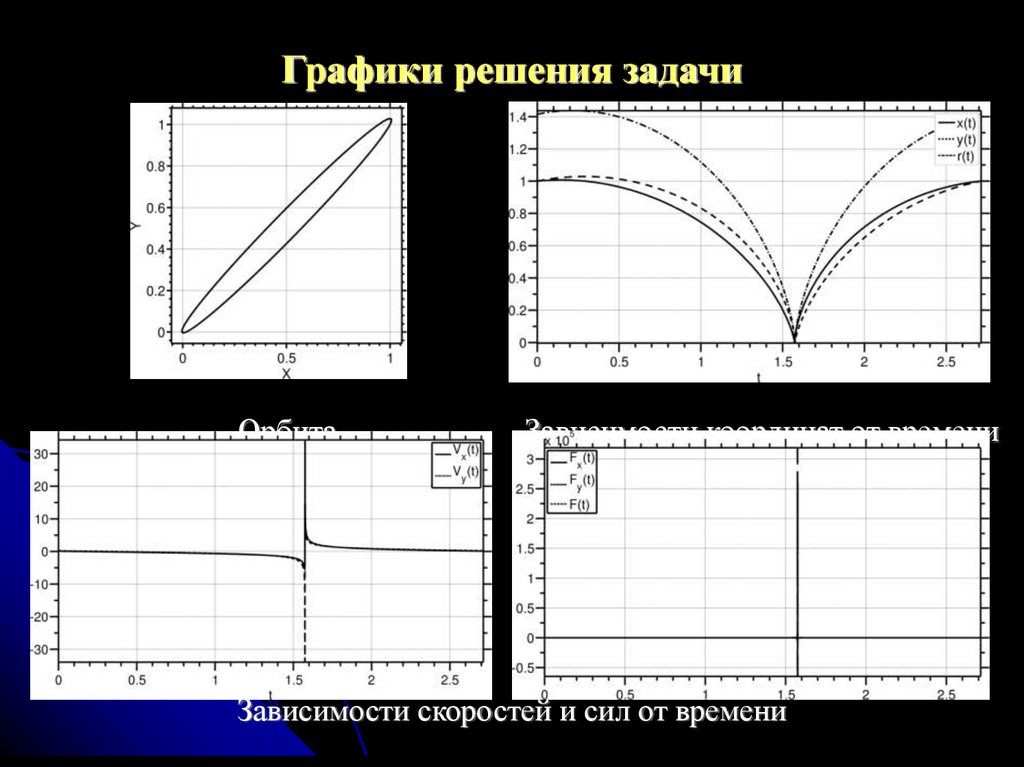
Графики решения задачиОрбита
Зависимости координат от времени
Зависимости скоростей и сил от времени
5.
Интуитивно ясно,что при численном решении задачи
расчетные точки должны плотно распределены
вблизи силового центра
и более редко в остальной части орбиты.
Предположим, что задача решена численным
методом
с постоянным шагом интегрирования.
Как в этом случае распределены расчетные точки
на приближенной орбите ?
6.
Для ответа на этот вопросне надо знать решение задачи.
Достаточно вспомнить второй закон Кеплера:
За равные промежутки времени
радиус-вектор,
направленный из силового центра в точки орбиты,
“заметает” равные площади.
Следовательно,
расчетные точки распределены наиболее плотно
вдали от силового центра,
там, где в этом нет необходимости.
Очевидно, что такой метод
с постоянным шагом интегрирования не эффективен.
7.
С одной стороны шаг должен бытьдосточно мал
для обеспечения требуемой точности
приближенного решения.
С другой стороны он должен быть
достаточно велик,
чтобы не допускать
бесполезную вычислительную работу.
8.
Существуют несколько подходовк исследованию актуальной проблемы
конструирования алгоритмов
автоматического выбора шага при численном
решении задачи Коши.
Один из них основан
на оценке зависимости локальной погрешности
приближенного решения
от величины шага интегрирования.
Другой подход
базируется на замене независимой переменной.
9.
Рассмотрим подходык решению проблемы автоматического выбора
шага интегрирования системы
обыкновенных дифференциальных уравнений
общего вида.
Затем сосредоточимся на случае
гамильтоновых уравнений.
10.
Оценка локальной погрешностии ее зависимость от шага интегрирования.
1. Правило Ричардсона*
______________________________________
*1. L. F. Richardson. The approximate arithmetical solutions by finite differences of physical
problems including differential equations, with an application to the stresses in a masonry dam.
Phil. Trans., A, 1910, vol. 210, p. 307-357.
2. L. F. Richardson. The deferred approach to the limit.
Phil. Trans., A, 1927, vol. 226, p. 299-349.
3. Э. Хайрер, С. Нерсетт, Г. Ваннер. Решение обыкновенных дифференциальных
уравнений. Нежесткие задачи. М.: Мир, 1990, 512 с.
.
11.
Как известно, для локальной погрешности eiчисленного метода порядка p
и достаточно малой величины шага i
имеет место следующее представление:
ei = X(ti) - Yi С(Yi) i p+1 + O( i p+2),
где C не зависит от
Для вычисления погрешности проведем расчет
выбранным методом из точки (ti, Yi)
для двух шагов величины 0.5 i.
Последовательно получим точки
(ti + 0.5 i, Yi,1/2) и (ti + i, Yi,2).
Затем выполним расчет с шагом i
и получим точку (ti + i, Yi,3).
12.
Погрешность Yi,1/2 представима в видеei,1/2 = X(ti + 0.5 i - Yi,1/2 С 2 - p - 1 i p + 1 + O( i p+2) (*).
Погрешность Yi,2 состоит из двух частей:
из погрешности первого шага
(E + 0.5 i X)ei,1/2
и погрешности вида (*), вычисленной при Yi,1 = Yi + O( i),
то есть (С + O( i))2 - p - 1 i p+1 + O( i p+2).
Поэтому
ei,2 = X(ti + i - Yi,2
(E + O( i))2 - p - 1 i p+1 + (С + O( i))2 - p - 1 i p+1 + O( i p+2) =
С 2 - p i p+1 + O( i p+2) (**).
Для одного шага величины i имеем:
ei,3 = X(ti + i - Yi,3 С i p + 1 + O( i p + 2) (***).
13.
Исключение C из (**) и (***)дает следующее выражение для погрешности ei,2:
ei,2 = X(ti + i - Yi,2 (Yi,2 - Yi,3)(2p - 1)-1 + O( i p + 2).
а равенство
X(ti + i - (Yi,2 (Yi,2 - Yi,3)(2p - 1)-1) = O( i p+2)
означает, что выражение
(Yi,2 (Yi,2 - Yi,3)(2p - 1)-1)
аппроксимирует
X(ti + i
с более высоким порядком p + 1.
Поэтому можно положить
Yi+1 Yi,2 или Yi+1 (Yi,2 (Yi,2 - Yi,3)(2p - 1)-1).
14.
Автоматический выбор шагана основе правила Ричардсона
Пусть имеется первоначальная величина шага i
В результате выполнения расчетов на двух шагах
величины 0.5 i и на одном шаге длины i получаем
Yi,2 , Yi,3 и выражение для локальной погрешности erri:
erri = Yi,2 - Yi,3 ym,i-1(2p - 1)-1 + O( i p + 2),
где ym,i = max(1, Yi Yi,2 ).
Величина erri сравнивается с допустимой величиной
погрешности tol и выбирается оптимальный шаг*
i = fs i tol/erri 1/(p+1), 0 < fs 1.
Затем выполняются расчеты с шагом i+1 = i
__________________________________________________________________________________________________________________________
*F. Ceschino. Modification de la longueur du pas dans l’integration numerique par es a pas lies.
Chiffres, 1961, 2, p. 101-106.
15.
Если для этого шага погрешность erri+1удовлетворяет неравенству
erri+1 tol,
то шаг одобряется и вычисления продолжаются.
Если выполняется неравенство
erri+1 tol,
то описанные выше вычисления
повторяются с шагом i
16.
Применение такой стратегии выбора шагапри решении задачи Коши
для гамильтоновых систем
оказалось неудовлетворительным.
Сравнение приближенных решений,
полученных методом с постоянным шагом
и методом с описанной выше
процедурой выбора шага, показало,
что на больших отрезках времени
дисбаланс полной энергии
в случае постоянного шага намного меньше
и точность приближенного решения намного выше.
17.
2. Вложенные методы Рунге-КуттыИдея заключается в том,
чтобы вместо использования правила Ричардсона
построить такие методы Р-К,
которые кроме приближенного решения Yi+1
определенного порядка точности p
давали бы приближенное решение Yi+1
более высокого порядка, чем Yi+1.
Эти решения можно было бы использовать
для оценки локальной погрешности и определения
величины шага интегрирования.
18.
Для решения задачи КошиdX/dt = X
X(0) = X0
применяют пару S – стадийных методов Рунге-Кутты
с одинаковыми разрешающими уравнениями
для неизвестных Ks
Ks = Yi + i(as,1K1+…+ as,SKS s = 1, …, S
и формулами вычисления приближенного решения
на следующем шаге
с различными наборами коэффициентов
Yi+1 = Yi + i(b1K1+…+ bSKS
Yi+1 = Yi + i(b1K1+…+ bSKS
19.
Индикатором локальной ошибки является векторEl i(Yi, i) = i((b1 - b1)K1+…+(bS - bS)KS
При исчезающе малых i
El i(Yi, i) с i i
Методам присваивается пара чисел p(q).
Первое число обозначает порядок аппроксимации Yi+1,
а второе – порядок апппроксимации Yi+1.
Как правило, q = p +1.
Шаг i при заданной абсолютной погрешности tol
можно определить из уравнений
Ks = Yi + i(as,1K1+…+ as,SKS
s = 1, …, S,
i (b1 – b1)K1+…+ (bS – bS)KS tol.
20.
Первые методы такого рода были предложены*Мерсоном RKM 4(5), Ческино RKC 2(4), Зоннефельдом RKZ 4(3).
Много методов было создано Фельбергом,
например, RKF 2(3), RKF 4(5).
Отмечу также хорошо зарекомендовавший себя
метод Дормана-Принса RKDOPR 5(4).
Таблицы Бутчера для этих методов
представлены на следующих слайдах.
----------------------------------------------------------------------------------------------------------------------------*1. R.Y. Merson. An operational method for the study of integration processes. Proc. Symp.
Data Processing, Weapons Reseach Establishment, Salisbury, Australia, 1957, p. 1-25.
2. F. Ceschino. Evaluation de l’erreur par pas dans les problemes differetiels.
Chiffres, 1962, vol. 5, p. 223-229
3. J.A. Zonneveld. Avtomatic integration of ordinary differential equations.
Report R743, Mathematisch Centrum, Postbus 4079, 1009AB Amsterdam, 1963.
4. E. Fehlberg. Low-order classical Runge-Kutta formulas with stepsize control
and their application to somei heat transfer problems.
NASA Technical Report 315, 1969; Computing, 1970, vol.6, h. 61-71.
5. J. R. Dormand, P. J. Prince. Afamily of embedded Runge-Kutta formulae.
J. Comp. Appl. Math. Vol. 6, p. 19-26.
21.
Таблицы Бутчера вложенных методов Рунге-Кутты0
1/3 1/3
1/3 1/6 1/6
1/2 1/8 0 3/8
1 1/2 0 - 3/2 2
1/2 0 - 3/2 2 0
1/6 0 0 2/3 1/6
Метод RKM 4(5)
0
1/2 1/2
1/2 0 1/2
1 0
0
1
3/4 5/32 7/32 13/32 - 1/32
1/6 1/3 1/3
1/6 0
- 1/2 7/3 7/3 13/6 - 16/3
Метод RKZ 4(3)
0
1/4 1/4
1/2 0 1/2
1 1 -2 2
1 -2 2 0
1/6 0 4/6 1/6
Метод RKC 2(4)
22.
Таблицы Бутчера вложенных методов Рунге-Кутты0
1/3 1/3
1/3 1/6 1/6
1/2 1/8 0 3/8
1 1/2 0 - 3/2 2
&
1/2 0 - 3/2 2 0
1/6 0 0 2/3 1/6
Метод RKF 4(5)
0
1/2 1/2
1/2 0 1/2
1 0
0
1
3/4 5/32 7/32 13/32 - 1/32
1/6 1/3 1/3
1/6 0
- 1/2 7/3 7/3 13/6 - 16/3
Метод RKDOPR 5(4)
23.
Для примера выведем формулы вложенных методовмалого порядка аппроксимации.
1. Рассмотрим таблицу Бутчера двухстадийных методов RK 1(2)
c1 a11 a12
c2 a21 a22
b1 b 2
b1 b 2
где c1 = a11 + a12, c2 = a21 + a22
и условия порядка b1 + b2 = 1, b1 + b2 = 1, b1c1 + b2c2 = 1/2.
Получаем
пятипараметрическое семейство неявных методов {b1, b1, a11, a12, a22}:
a21 = (1/2 - b1(a11+ a12) - (1 - b1)a22)(1 - b1)-1;
трехпараметрическое семейство однократно диагональных неявных методов
{b1, b1, a}:
a11 = a22 = a, a12 = 0, a21 = (1/2 - a)(1 - b1)-1;
двухпараметрическое семейство явных методов {b1, b1}:
a11 = a22 = a12 = 0, a21 = 1/2(1 – b1)-1.
24.
2. Рассмотрим таблицу Бутчера трехстадийных методов RK 2(3)c1 a11 a12 a13
c2 a21 a22 a23
c3 a31 a32 a33
b1 b2 b3
b1 b2 b3,
где c1 = a11 + a12+ a13, c2 = a21 + a22+ a23, c3 = a31 + a32+ a33,
и условия порядка
b1 + b2 + b3 = 1, b1 + b2 + b3 = 1,
b1c1 + b2c2 + b3c3 = 1/2, b1c1 +
b2c2 + b3c3 = 1/2,
b1c12 + b2c22 + b3c32 = 1/3,
b1a11c1 + b1a12c2 + b1a13c3 + b2a21c1 + b2a22c2+
b2a23c3+ b3a31c1+ b3a32c2+ b3a33c3 = 1/6.
25.
Из условий порядка следует, чтоb2 = 1 - b1 - b3, b2 = 1 - b1 - b3,
b1(a11+ a12+ a13) + (1 - b1 - b3)(a21+ a22+ a23) + b3(a31+ a32+ a33) = 1/2,
b1(a11 + a12+ a13) + (1 - b1 - b3)(a21 + a22+ a23) + b3(a31 + a32+ a33) = 1/2,
b1(a11 + a12+ a13)2 + b2(a21 + a22+ a23)2 + b3(a31 + a32+ a33)2 = 1/3,
b1a11(a11 + a12+ a13) + b1a12(a21 + a22+ a23) + b1a13(a31 + a32+ a33) +
b2a21(a11 + a12+ a13) + b2a22(a21 + a22+ a23) + b2a23(a31 + a32+ a33) +
b3a31(a11 + a12+ a13) + b3a32(a21 + a22+ a23) + b3a33(a31 + a32+ a33) = 1/6.
Из последних трех равенств получаем уравнения
для выделенных a21, a31, a32
26.
b3a31 = A - b2a21- b3a32,b2a212 + 2b2a21(a22+ a23+ a33) - b3a322 + 2Aa32 - 2b2a21a32 = B =
1/3 - a33- b1c12 + 2b1a33c1- b2(a222 + a232 + 2a22a23- 2a22a33- 2a23a33) +
b3a332,
b32a21a32 + [b1b3a12 + b2b3a22 - b1b2a13 - b22a23 - b2b3a33]a21
+ b32(a22 + a23 - a11 - a12 - a13)a32
= 1/6b3 + b1b2(a13a22 + 2a13a23 + a11a23 + a12a23)
- b1b3(a11c1+ a12a22+ a12a23- c12 - a33c1) +
b2b3(a22a33 + a22c1 + a23a33 + a23c1 - a222 - a22a23)
- 1/2b1a13 - 1/2b2a23 - 1/2b3(a33+ c1) + b12a13c1+ b22(a22+ a23)a23+
b32a33c1 =
D,
A = 1/2 - b1c1 - b2(a22+ a23) - b3a33,
27.
b2a212 + 2b2a21(a22+ a23+ a33) - b3a322 + 2Aa32 - 2b2a21a32 = B,b32a21a32 - [a23 + b1(a13 - 2a23) + b3(- a22 - 2a23 + a33) + b12(- a13 + a23)
+ b1b3(- a12 - a13 + a22 + 2a23 - a33) + b32(a22 + a23 - a33)]a21
- b32(a11 + a12 + a13 - a22 - a23 )a32 = D,
b2b32a212 - 2b2[a23 + b1(a13 - 2a23) - b3(a22 + 2a23 - a33)
+ b12(- a13 + a23) + b1b3(- a12 - a13 + a22 + 2a23 + a33)]a21
- b33a322 + 2b32[1/2 - a11 - a12 - a13 + b3(a11 + a12 + a13 - a33)]a32 =
Bb32 + 2D(1 - b1 - b3),
b3a31 = A - b2a21- b3a32,
A = 1/2 - a22 - a23 - b1(a11 + a12 + a13 - a22 - a23) + b3(a22+ a23 - a33),
28.
Заманчиво построитьвложенные симметрично-симплектические
методы Рунге-Кутты
для решения задачи Коши для гамильтоновых систем.
Однако, эта задача не имеет решения, так требование
иметь одну и ту же систему разрешающих уравнений для
неизвестных Ks, s = 1, …, S
при разных наборах коэффициентов {b} и {b}
является слишком жестким .
Чтобы убедиться в этом
достаточно вспомнить структуру матрицы А
в таблице Бутчера для симметрично-симплектических
методов Рунге-Кутты.
29.
Замена независимой переменнойМожно получить приближенное решение задачи на сетке
с переменным шагом i
на основе замены независимой переменной t t’.
Пусть dt = s(X)dt’, 0 < s(X).
Тогда исходная задача
dX/dt = (X), X(0) = X0
для t’ 0 принимает вид:
dX/dt’ = s(X) (X), dt/dt’ = s(X),
X(0) = X0, t(0) = 0.
Функцию s = s(X) называют функцией выбора шага.
Применение численного метода c постоянным шагом ( t’) для
решения последней задачи дает приближенное решение исходной
задачи на сетке с переменным шагом
(i+1) t’
i = s(X( ))d .
i t’
30.
Если исходная система является гамильтоновойdP/dt = - ( H(P, R)/ R)T,
dR/dt = ( H(P, R)/ P)T,
P(0) = P0, R(0) = R0,
то после замены независимой переменной
получаем новую задачу вида:
dP/dt’ = - s(P, R)( H(P, R)/ R)T,
dR/dt’ = s(P, R)( H(P, R)/ P)T, (*)
dt/dt’ = s(P, R),
P(0) = P0, R(0) = R0, t(0) = 0.
Приближенное решение этой задачи с постоянным шагом ( t’)
дает решение исходной задачи на сетке с переменным шагом
(i+1) t’
i = s(P( ), R( ))d .
i t’
31.
Применим к новой задаче метод Верле.Получим уравнения для Pi+1/2, Ri+1
Pi+1/2 = Pi - 0.5 t’s(Pi+1/2, Ri)( Pi+1/2, Ri / R)T
Ri+1 = Ri + 0.5 t’ s(Pi+1/2, Ri)( Pi+1/2, Ri / P)T
s(Pi+1/2, Ri+1)( Pi+1/2, Ri+1 / P)T
и явные формулы для вычисления Pi+1, ti+1
Pi+1 = Pi+1/2 - 0.5 t’s(Pi+1/2, Ri+1)( Pi+1/2, Ri+1 / R)T
ti+1 = ti + 0.5 t’[s(Pi, Ri) + s(Pi+1, Ri+1)].
Уравнения для неизвестных Pi+1/2, Ri+1 могут быть решены
последовательно итерационным методом
с начальными приближениями
Pi+1/2(0) = Pi, Ri+1(0) = Ri + 0.5 t’ s(Pi+1/2, Ri)( Pi+1/2, Ri / P)T,
например, методом Ньютона.
32.
В случае разделенной функции ГамильтонаH = 0.5P T M -1P + U (R)
имеем следующие уравнения для Pi+1/2, Ri+1
Pi+1/2= Pi - 0.5 t’s(Pi+1/2, Ri)( U(Ri)/ R)T
Ri+1= Ri+ 0.5 t’[s(Pi+1/2, Ri) + s(Pi+1/2, Ri+1)]M -1Pi+1/2
с начальными приближениями для итерационных процессов
Pi+1/2(0) = Pi, Ri+1(0) = Ri + 0.5 t’s(Pi+1/2, Ri)M -1Pi+1/2
и явные формулы для вычисления Pi+1, ti+1
Pi+1 = Pi+1/2- 0.5 t’s(Pi+1/2, Ri+1)( U(Ri+1)/ R)T,
ti+1 = ti + 0.5 t’[s(Pi, Ri) + s(Pi+1, Ri+1)]
33.
Рассмотренный выше подходк разработке адаптивных численных методов
имеет существенный недостаток.
Если исходная система является удобной для анализа
гамильтоновой системой
dZ/dt = - J( (Z))T,
то преобразованная система уравнений движения
dZ/dt’ = - s(Z)J( (Z))T,
dt/dt’ = s(Z)
теряет это свойство при любой нетривиальной функции
выбора шага s = s(Z).
34.
Рассмотрим следующий вопрос.При каких функциях выбора шага s = s(Z)
существует функция H ’(Z)
такая, что
s(Z)( (Z))T = ( ’(Z))T ?
35.
Необходимым условиемпотенциальности векторного поля s(Z)( (Z))T
является симметричность его матрицы Якоби [??]
(s(Z)( (Z))T) = ( (Z))T s(Z) + s(Z) (Z).
Матрица (Z) дважды непрерывно дифференцируемой
функции (Z) является симметричной.
Для выполнения необходимого условия
требуется симметричность матрицы
( (Z))T s(Z),
образованной столбцом ( (Z))T
и строкой s(Z).
Это возможно в случае параллельности векторов
(Z) и s(Z):
(Z) k s(Z), k – const.
36.
Если так,то в силу кососимметричности матрицы J имеем
ds(Z)/dt = - k s(Z)J( s(Z))T 0,
Итак, преобразованная система
является гамильтоновой лишь в случае, когда
функция выбора шага является тривиальной
s(Z) – const.
Полученный ответ нас не устраивает.
37.
Расширение фазового пространства*Расширим фазовое пространство {P, R}.
В {P, R} введем время t как дополнительную координату R*
и дополнительный импульс P*.
Получим новое фазовое пространство {P, P*, R, R*}.
_________________________________________________
* 1. K. F. Sundman. Memoire sur le probleme des trois corp.
Acta Math. 1912, 36, 105-179.
2. K. Zare, V. Szebehely. Time transformations in the extended phase-space.
Celestial Mechanics and Dynamical Astronomy, 1975, 11, 469-482
3. E. Hairer. Variable time step integration with symplectic methods.
Applied Numerical Mathematics, 1997, 25 (2-3), 219-227
4. S. Reich. Backward error analysis for numerical integrators.
SIAM J. on Numerical Analysis, 1999, 36 (5), 1549-1570
38.
Найдем новую функцию ГамильтонаH’(P*, P, R*, R)
такую, чтобы выполнялись следующие равества:
dP0/dt’ = - ( H’(P, P*, R, R*)/ R*)T,
dP/dt’ = - ( H’(P, P*, R, R*)/ R)T =
- s(P, R)( H(P, R)/ R)T,
dR/dt’ = ( H’(P, P*, R, R*)/ P*)T =
s(P, R)( H(P, R)/ P)T,
dR*/dt’ = H’(P, P*, R, R*)/ P* =
s(P, R).
39.
Рассмотрим функциюH’(P, P*, R, R*) = s(P, R)[H(P, R) + P*].
Эта функция является функцией Гамильтона
для системы уравнений следующего вида:
dP*/dt’ = - H’/ R* = 0,
dP/dt’ = - ( H’/ R)T =
- s(P, R)( H(P, R)/ R)T - s(P, R)/ R)T[H(P, R) + P*],
dR/dt’ = ( H’/ P)T =
s(P, R)( H(P, R)/ P)T + s(P, R)/ R)T[H(P, R) + P*],
dR*/dt’ = H’/ P* = s(P, R).
Если при t’ = 0 P* = - H0 = - H(P0, R0),
то H(P, R) + P* 0 и уравнения движения для функции H ’
совпадают с новой системой уравнений (*).
40.
Вместо исходной задачи для гамильтоновой системыdP/dt = - ( H(P, R)/ R)T,
dR/dt = ( H(P, R)/ P)T,
P(0) = P0, R(0) = R0,
будем рассматривать новую задачу (**):
dP/dt’ = - ( H’/ R)T =
- {s(P, R)( H(P, R)/ R)T + s(P, R)/ R)T[H(P, R) - H0]},
dR/dt’ = ( H’/ P)T =
s(P, R)( H(P, R)/ P)T + s(P, R)/ P)T[H(P, R) - H0],
dt/dt’ = H’/ P0 = s(P, R),
P(0) = P0, R(0) = R0, t(0) = 0,
где s = s(P, R) - известная функция выбора шага,
H’(P, - H0, R, R*) = s(Z)(H(P, R) - H0) - новая функция Гамильтона.
41.
Описанное выше преобразование Зюндманалежит в основе ряда адаптивных численных
методов решения задачи Коши
для гамильтоновых систем.
Для численного решения задачи (**)
применяют симплектические численные методы
с постоянным шагом t’,
составляющим малую долю
минимального характерного времени задачи.
К таким методам относится метод Верле с
переменным шагом интегрирования.
42.
Метод Верлес автоматическим выбором шага
Применим к системе (**)
с неразделенной функцией Гамильтона H(P, R)
dP/dt’ = - ( H’/ R)T =
- [( (P, R) - 0)( s(P, R)/ R)T + s(P, R)( H(P, R)/ R)T],
dR/dt’ = ( H’/ R)T =
[( (P, R) - 0)( s(P, R)/ P)T + s(P, R)( H(P, R)/ P )T],
dt/dt’ = H’/ P0 = s(P, R)
метод Верле.
43.
Вычислительный алгоритом заключается в следующем.1. Итерационным методом решается уравнение для Pi+1/2
Pi+1/2 = Pi - 0.5 t’[( (Pi+1/2, Ri) - 0)( s(Pi+1/2, Ri)/ R)T +
s(Pi+1/2, Ri)( H(Pi+1/2, Ri)/ R)T].
2. По явной формуле вычисляется Ri+1/2:
Ri+1/2 = Ri + 0.5 t’[( (Pi+1/2, Ri) - 0)( s(Pi+1/2, Ri)/ P)T +
s(Pi+1/2, Ri)( H(Pi+1/2, Ri)/ P )T].
3. Итерационным методом решается уравнение для Ri+1
Ri+1 = Ri+1/2 + 0.5 t’[( (Pi+1/2, Ri+1) - 0)( s(Pi+1/2, Ri+1)/ P)T +
s(Pi+1/2, Ri+1)( H(Pi+1/2, Ri+1)/ P )T].
. По явным формулам вычисляются Pi+1: и ti+1:
Pi+1 = Pi+1/2 - 0.5 t’[( (Pi+1/2, Ri+1) - 0))( s(Pi+1/2, Ri+1)/ R)T +
s(Pi+1/2, Ri+1)( H(Pi+1/2, Ri+1)/ R)T],
ti+1 = ti + 0.5 t’[s(Pi, Ri) + s(Pi+1, Ri+1)].
44.
Метод Верле с автоматическим выбором шагадля разделенной функции Гамильтона
Пусть имеется функция Гамильтона H = 0.5PTM -1P + U(R),
задача Коши для гамильтоновой системы
dP/dt = - ( U/ R)T, dR/dt = M -1P ,
P(0) = P0, R(0) = R0
и функция выбора шага s = s(P, R).
Тогда система (**) принимает вид:
dP/dt’ =
- [(0.5PTM -1P + U(R) - 0)( s(P, R)/ R)T + s(P, R)( U(R)/ R)T],
dR/dt’ =
(0.5PTM -1P + U(R) - 0)( s(P, R)/ P)T + s(P, R)M -1P,
dt/dt’ = s(P, R).
45.
Применим метод Верле и получим вычислительный алгоритм.1. Итерационным методом решается уравнение для Pi+1/2
Pi+1/2= Pi - 0.5 t’[(0.5Pi+1/2TM -1Pi+1/2+ U(Ri) - 0)( s(Pi+1/2, Ri)/ R)T
+ s(Pi+1/2, Ri)( U(Ri)/ R)T]
2.По явной формуле вычисляется Ri+1/2:
Ri+1/2= Ri + 0.5 t’[(0.5Pi+1/2TM -1Pi+1/2+ U(Ri) - 0)( s(Pi+1/2, Ri)/ P)T
+ s(Pi+1/2, Ri)M -1Pi+1/2]
3.Итерационным методом решается уравнение для Ri+1
Ri+1= Ri+1/2+ 0.5 t’[(0.5Pi+1/2TM -1Pi+1/2+ U(Ri+1) - 0)
( s(Pi+1/2, Ri+1)/ P )T + s(Pi+1/2, Ri+1)M -1Pi+1/2],
4.По явным формулам вычисляются Pi+1 и ti+1 :
Pi+1 = Pi+1/2- 0.5 t’[(0.5Pi+1/2TM -1Pi+1/2+ U(Ri+1) - 0)
( s(Pi+1/2, Ri+1)/ R)T + s(Pi+1/2, Ri+1)( U(Ri+1)/ R)T],
ti+1 = ti + 0.5 t’[s(Pi, Ri) + s(Pi+1, Ri+1)].
46.
Метод Верле с автоматическим выбором шагадля разделенной функции Гамильтона
и функцией выбора шага не зависящей от
импульсов
Для задачи Коши
dP/dt = - ( U/ R)T, dR/dt = M -1P ,
P(0) = P0, R(0) = R0
и функции выбора шага s = s(P, R)
система (**) имеет вид:
dP/dt’ =
- (0.5PTM -1P + U(R) - 0)( s(R)/ R)T + s(R)( U(R)/ R)T,
dR/dt’ = s(R)M -1P,
dt/dt’ = s(R).
47.
Применение метода Верле дает уравнениядля определения Pi+1/2 и Ri+1:
Pi+1/2 = Pi - 0.5 t’[(0.5Pi+1/2TM -1Pi+1/2 + U(Ri) - 0)( s(Ri)/ R)T +
s(Ri)( U(Ri)/ R)T],
Ri+1= Ri + 0.5 t’(s(Ri) + s(Ri+1))M -1Pi+1/2,
а также явные формулы для вычисления Pi+1 и ti+1:
Pi+1 = Pi+1/2- 0.5 t’[(0.5Pi+1/2TM -1Pi+1/2+ U(Ri+1) - 0)( s(Ri+1)/ R)T
+ s(Ri+1)( U(Ri+1)/ R)T],
ti+1 = ti + 0.5 t’[s(Ri) + s(Ri+1)].
Остановимся на решении уравнений.
48.
Рассмотрим уравнения для определения Pi+1/2:Pi+1/2 = Pi - 0.5 t’[(0.5Pi+1/2TM -1Pi+1/2 + U(Ri) - 0)( s(Ri)/ R)T +
s(Ri)( U(Ri)/ R)T]. (1*)
Обратим внимание на то,
что неизвестные Pi+1/2 можно вычислить по явным формулам,
если известна скалярная величина = Pi+1/2TM -1Pi+1/2:
Pi+1/2= Pi - 0.5 t’[(0.5 + U(Ri) - 0)( s(Ri)/ R)T +
s(Ri)( U(Ri)/ R)T].
Из (1*) получим квадратное уравнение для .
= Pi+1/2TM -1Pi+1/2 =
{PiT - 0.5 t’[(0.5 + U(Ri) - 0) s(Ri)/ R + s(Ri) U(Ri)/ R]}
{M -1Pi - 0.5 t’[(0.5 + U(Ri) - 0)M -1( s(Ri)/ R)T +
s(Ri)M -1( U(Ri)/ R)T]}
или
49.
A 2 - B + C = 0,где
A = 1/16a2( t’)2, B = 1 + 0.5b1( t’) - 0.25b2( t’)2,
C = PiTM -1Pi - c1( t’) + 0.25c2( t’)2,
a2 = ( s(Ri)/ R)M -1( s(Ri)/ R)T, b1 = PiTM -1( s(Ri)/ R)T,
b2 = (U(Ri) - 0)( s(Ri)/ R)M -1( s(Ri)/ R)T
+ s(Ri)( s(Ri)/ R)M -1( U(Ri)/ R)T,
c1 = (U(Ri) - 0)PiTM -1( s(Ri)/ R)T + s(Ri)PiTM -1( U(Ri)/ R)T,
c2 = (U(Ri) - 0)2( s(Ri)/ R)M -1( s(Ri)/ R)T
+ 2(U(Ri) - 0)s(Ri)( s(Ri)/ R)M -1( U(Ri)/ R)T
+ s2(Ri)( U(Ri)/ R)M -1( U(Ri)/ R)T.
Нужное решение квадратного уравнения имеет вид:
= 2Csign(B)( B + (B 2 - 4AC)0.5)-1.
50.
Рассмотрим уравненияRi+1= Ri + 0.5( t’)(s(Ri) + s(Ri+1))M -1Pi+1/2.
Неизвестные Ri+1 можно найти по явной формуле
Ri+1= Ri + 0.5( t’)(s(Ri) + )M -1Pi+1/2
если известна величина s(Ri+1) =
Неизвестная удовлетворяет скалярному уравнению
- s(Ri + 0.5( t’)(s(Ri) + )M -1Pi+1/2) = 0.
Решение этого уравнения может быть найдено итерационным
методом, например методом Ньютона:
m+1 = m - ( m - s(Ri + 0.5 t’(s(Ri) + m )M -1Pi+1/2))
(1 - 0.5 t’( s(Ri + 0.5 t’(s(Ri) + m )M -1Pi+1/2)/ R)M -1Pi+1/2)-1,
m = 0, 1, … ; m – номер итерации.
В качестве начального приближения
можно использовать s(Ri).
51.
Итак, неявный метод может быть реализован следующимобразом. На каждом шаге
1. по явной формуле вычисляется величина
= 2C(B + (B 2 – 4AC)0.5)-1,
2. находится решение нелинейного скалярного уравнения
- s(Ri + 0.5( t’)(s(Ri) + )M -1Pi+1/2) = 0,
3. неизвестные Pi+1/2 Ri+1, Pi+1, ti+1 вычисляются по формулам:
Pi+1/2= Pi - 0.5 t’[(0.5 + U(Ri) - 0)( s(Ri)/ R)T +
s(Ri)( U(Ri)/ R)T],
Ri+1= Ri + 0.5( t’)(s(Ri) + )M -1Pi+1/2 ,
Pi+1 = Pi+1/2- 0.5 t’[(0.5 + U(Ri+1) - 0)
( s(Ri+1)/ R)T + ( U(Ri+1)/ R)T],
ti+1 = ti + 0.5 t’[s(Ri) + ].
52.
Функции выбора шагаИспользуются различные функции выбора шага*.
1. s(Ri) = i , 1
где
i (x1,i2 + y1,i2 + z1,i2 +…+ xN,i2 + yN,i2 + zN,i2)1/2,
s(Ri)/ R = Ri = s (Ri)Ri.
2. s(Ri) = [H0 - U(Ri)]- 1/2,
s(Ri)/ R = 0.5[H0 - U(Ri)]-3/2 U(Ri)/ R =
0.5s3(Ri)( U(Ri)/ R).
----------------------------------------------------------------------------------------------------------------------------- ---------
* 1. R. I. J. MacLeod, J. M. Sanz-Serna. Geometrically derived difference formulae for the
numerical integration of trajectory problems. IMA J. Numer. Anal., 1982, 2, 357-370
2.W. Huang, B. Leimkuhler. The adaptive Verle method. SIAM J.Sci.Comput.,1997,18, 239-256
3. T. Holder, B. Leimkuhler, S. Reich. Explicit variable step-size and time reversible integration.
Appl. Numer. Math., 2001, 367-377
4. E. Hairer, C. Lubich, G. Wanner. Geometric Numerical Integration. 2002, Springer-Verlag, 515
53.
3. s(Pi, Ri) = [PiTM -2Pi + ( U(Ri)/ R)( U(Ri)/ R)T]-1/2,s(Pi, Ri)/ P =
- 0.5[PiTM -2Pi + ( U(Ri)/ R)( U(Ri)/ R)T]-3/2PiTM-2 =
- 0.5s3(Pi, Ri)PiTM -2,
s(Pi, Ri)/ R =
- 0.5[PiTM -2Pi + ( U(Ri)/ R)( U(Ri)/ R)T]-3/2
( U(Ri)/ R)( U(Ri)/ R2) =
- 0.5s3(Pi, Ri)( U(Ri)/ R)( U(Ri)/ R2).
Эта функция обеспечивает эквидистантность
расчетных точек
в исходном фазовом пространстве {P, R}.
54.
4. s(Pi, Ri) = [1 + PiTM -2Pi + ( U(Ri)/ R)( U(Ri)/ R)T]-1/2,s(Pi, Ri)/ P =
- 0.5[1 + PiTM -2Pi + ( U(Ri)/ R)( U(Ri)/ R)T]-3/2PiTM -2 =
s3(Pi, Ri)PiTM -2,
s(Pi, Ri)/ R =
- 0.5[1 + PiTM -2Pi + ( U(Ri)/ R)( U(Ri)/ R)T]3/2( U(R )/ R) ( U(R )/ R2) =
i
i
s3(Pi, Ri)( U(Ri)/ R)( U(Ri)/ R2).
Эта функция обеспечивает эквидистантность
расчетных точек
в исходном расширенном фазовом пространстве {P, R, t}.
55.
В качестве примера рассмотрим исходную задачуdvx/dt = - xr -3, dvy/dt = - yr -3,
dx/dt = vx, dy/dt = vy,
x(0) = х0, y(0) = y0, vx(0) = vx,0, vy(0) = vy,0
с первыми интегралами
lz = xvy - yvx, H = 0.5(vx2 + vy2) - r -1,
ex = vylz - xr -1, ey = - vxlz - yr -1, 2Hlz = e2 - где
v2 = vx2 + vy2, r = (x2 + y2)0.5
и функциями выбора шага
1. s(x, y) = r = ( x2 + y2)0.5 , 1
1’. s’(x, y) = r = ( x2 + y2)0.5,
1”. s”(x, y) = r 2 = x2 + y2,
2. s(x, y) = v = (vx2 + vy2)0.5 , 1
2’. s’(vx, vy) = v = (vx2 + vy2)0.5, 2”. s”(x, y) = 2-0.5(H0 + r -1)-0.5,
3’. s’(vx, vy, x, y) = (vx2 + vy2 + r -4)-0.5,
3”. s”(x, y) = (2H0 + 2 r + r -4)-0.5,
4’. s’(vx, vy, x, y) = (1 + vx2 + vy2 + r -4)-0.5 ,
4”. s”(x, y) = (1 + 2H0 + 2 r + r -4)-0.5.
56.
1. s = r = (x2 + y2)0.5 , 1s/ vx = 0, s/ vy = 0, s/ x = r x, s/ y = r y ;
1’. s’ = r = (x2 + y2)0.5,
s’/ vx = 0, s’/ vy = 0, s’/ x = r x, s’/ y = r y ;
1”. s” = r2 = x2 + y2,
s”/ vx = 0, s”/ vy = 0, s”/ x = 2x, s”/ y = 2y ;
2. s(vx, vy) = v - = (vx2 + vy2)-0.5 , 1
s/ vx = - v vx, s/ vy = - v vy, s/ x = 0, s/ y = 0 ;
2’. s’(vx, vy) = v -1 = (vx2 + vy2)-0.5,
s/ vx = - v vx, s/ vy = - v vy, s/ x = 0, s/ y = 0 ;
2”. s” = 2-1/2[H0 + r -1]- 1/2,
s”/ vx = 0, s”/ vy = 0,
s”/ x = 2-3/2[H0 + r -1]-3/2 r -3x, s”/ y = 2-3/2[H0 + r -1]-3/2 r -3y;
3’. s’(vx, vy, x, y) = (vx2 + vy2 + r - 4)-0.5,
s’/ vx = - s’) vx, s’/ vy = - s’) vy,
s’/ x = 2 s’) r -6x, s’/ y = 2 s’) r -6y;
3”. s”(x, y) = (2H0 + 2 r -1 + r -4)-0.5,
s”/ vx = 0, s”/ vy = 0, s”/ x = xr -3(s”)-3(1+2 r -3)x, s”/ y = xr -3(s”)-3(1+2 r -3)y;
57.
4’. s’(vx, vy, x, y) = (1 + vx2 + vy2 + r -4)-0.5 ,s/ vx = - (s’)3vx, s/ vy = - (s’)3vy, s’/ x = 2(s’)3 r -6x, s’/ y = 2(s’)3 r -6y;
4”. s”(x, y) = (1 + 2H0 + 2 r -1 + r -4)-0.5,
s”/ vx = 0, s”/ vy = 0,
s”/ x = (s”)3[1 + 2 r -3] r -3x, s”/ y = (s”)3[1 + 2 r -3] r -3y;
58.
1. В случае s = r = (x2 + y2)0.5 , 1 применение метода Верле к системеdvx/dt = - [(0.5v2 - r -1 - 0)( s/ x) + s r -3x],
dvy/dt = - [(0.5v2 - r -1 - 0)( s/ y) + s r -3y],
dx/dt = svx, dy/dt = svy, dt/dt’ = s
с функцией Гамильтона H = s(0.5v2 - r -1 - 0)
дает уравнения для vx,i+1/2, vy,i+1/2, xi+1, yi+1:
vx,,i+1/2 = vx,,i - 0.5 t’[(0.5vi+1/22 - ri -1 - 0) -1 ri + 1] ri -3xi,
vy,,i+1/2 = vy,,i - 0.5 t’[(0.5vi+1/22 - ri -1 - 0) -1 ri + 1] ri -3yi,
xi+1= xi + 0.5 t’[ri + ri+1 ]vx,,i+1/2, yi+1= yi + 0.5 t’[ri + ri+1 ]vy,,i+1/2,
а также явные формулы для вычисления vx,i+1, vy,i+1 и ti+1:
vx,,i+1 = vx,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1 -1 - 0) -1 ri+1 + 1] ri+1 -3xi+1,
vy,,i+1 = vy,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1 -1 - 0) -1 ri+1 + 1] ri+1 -3yi+1,
ti+1 = ti + 0.5 t’[ri ri+1 ].
59.
1. В случае s = r = (x2 + y2)0.5 , 1 применение метода Верле к системеdvx/dt = - [(0.5v2 - r -1 - 0)( s/ x) + s r -3x],
dvy/dt = - [(0.5v2 - r -1 - 0)( s/ y) + s r -3y],
dx/dt = svx, dy/dt = svy, dt/dt’ = s
с функцией Гамильтона H = s(0.5v2 - r -1 - 0)
дает уравнения для vx,i+1/2, vy,i+1/2, xi+1, yi+1:
vx,,i+1/2 = vx,,i - 0.5 t’[(0.5vi+1/22 - ri -1 - 0) -1 ri + 1] ri -3xi,
vy,,i+1/2 = vy,,i - 0.5 t’[(0.5vi+1/22 - ri -1 - 0) -1 ri + 1] ri -3yi,
xi+1= xi + 0.5 t’[ri + ri+1 ]vx,,i+1/2, yi+1= yi + 0.5 t’[ri + ri+1 ]vy,,i+1/2,
а также явные формулы для вычисления vx,i+1, vy,i+1 и ti+1:
vx,,i+1 = vx,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1 -1 - 0) -1 ri+1 + 1] ri+1 -3xi+1,
vy,,i+1 = vy,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1 -1 - 0) -1 ri+1 + 1] ri+1 -3yi+1,
ti+1 = ti + 0.5 t’[ri ri+1 ].
60.
1. В случае s = r = (x2 + y2)0.5 , 1 применение метода Верле к системеdvx/dt = - [(0.5v2 - r -1 - 0)( s/ x) + s r -3x],
dvy/dt = - [(0.5v2 - r -1 - 0)( s/ y) + s r -3y],
dx/dt = svx, dy/dt = svy, dt/dt’ = s
с функцией Гамильтона H = s(0.5v2 - r -1 - 0)
дает уравнения для vx,i+1/2, vy,i+1/2, xi+1, yi+1:
vx,,i+1/2 = vx,,i - 0.5 t’[(0.5vi+1/22 - ri -1 - 0) -1 ri + 1] ri -3xi,
vy,,i+1/2 = vy,,i - 0.5 t’[(0.5vi+1/22 - ri -1 - 0) -1 ri + 1] ri -3yi,
xi+1= xi + 0.5 t’[ri + ri+1 ]vx,,i+1/2, yi+1= yi + 0.5 t’[ri + ri+1 ]vy,,i+1/2,
а также явные формулы для вычисления vx,i+1, vy,i+1 и ti+1:
vx,,i+1 = vx,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1 -1 - 0) -1 ri+1 + 1] ri+1 -3xi+1,
vy,,i+1 = vy,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1 -1 - 0) -1 ri+1 + 1] ri+1 -3yi+1,
ti+1 = ti + 0.5 t’[ri ri+1 ].
61.
1’. Если тоvx,,i+1/2 = vx,,i - 0.5 t’[(0.5vi+1/22 - ri -1 - 0) -1 ri + 1] ri-2xi,
vy,,i+1/2 = vy,,i - 0.5 t’[(0.5vi+1/22 - ri -1 - 0) -1 ri + 1] ri-2yi,
xi+1= xi + 0.5 t’[ri + ri+1]vx,,i+1/2, yi+1= yi + 0.5 t’[ri + ri+1]vy,,i+1/2,
а также явные формулы для вычисления vx,i+1, vy,i+1 и ti+1:
vx,,i+1 = vx,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1 -1 - 0) -1 ri+1 + 1] ri+1-2xi+1,
vy,,i+1 = vy,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1 -1 - 0) -1 ri+1 + 1] ri+1-2yi+1,
ti+1 = ti + 0.5 t’[ri ri+1].
62.
1”. Если = тоvx,,i+1/2 = vx,,i - 0.5 t’[(0.5vi+1/22 - ri-1 - 0)2 -1ri + 1] ri-1xi,
vy,,i+1/2 = vy,,i - 0.5 t’[(0.5vi+1/22 - ri-1 - 0)2 -1ri + 1] ri-1yi,
xi+1= xi + 0.5 t’[ri + ri+1 ]vx,,i+1/2, yi+1= yi + 0.5 t’[ri + ri+1 ]vy,,i+1/2,
а также явные формулы для вычисления vx,i+1, vy,i+1 и ti+1:
vx,,i+1 = vx,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1-1 - 0)2 -1ri+1 + 1] ri+1-1xi+1,
vy,,i+1 = vy,,i+1/2 - 0.5 t’[(0.5vi+1//22 - ri+1-1 - 0)2 -1ri+1 + 1] ri+1-1yi+1,
ti+1 = ti + 0.5 t’[ri ri+1 ].
63.
4’. В случае s = (1 + vx2 + vy2 + r -4)-0.5 применение метода Верле к системеdvx/dt = - [(0.5v2 - r -1 - 0)( s/ x) + s r -3x],
dvy/dt = - [(0.5v2 - r -1 - 0)( s/ y) + s r -3y],
dx/dt = (0.5v2 - r -1 - 0)( s/ vx) + svx, dy/dt = (0.5v2 - r -1 - 0)( s/ vy) + svy,
dt/dt’ = s с функцией Гамильтона H = s(0.5v2 - r -1 - 0)
дает уравнения для vx,i+1/2, vy,i+1/2, xi+1, yi+1:
vx,,i+1/2 = vx,,i - 0.5 t’[2(0.5vi+1/22 - ri -1 - 0)si -3 ri -6xi +
(1 + 2H0 + 2 ri + ri -4)-0.5 ri -3xi],
vy,,i+1/2 = vy,,i - 0.5 t’[2(0.5vi+1/22 - ri -1 - 0)si -3 ri -6yi +
(1 + 2H0 + 2 ri + ri -4)-0.5 ri -3yi],
xi+1= xi + 0.5 t’[(1 + 2H0 + 2 ri + ri -4)-0.5 + (1 + 2H0 + 2 ri+1 + ri+1 -4)-0.5]vx,,i+1/2,
yi+1= yi + 0.5 t’[(1 + 2H0 + 2 ri + ri -4)-0.5 + (1 + 2H0 + 2 ri+1 + ri+1 -4)-0.5]vy,,i+1/2,
а также явные формулы для вычисления vx,i+1, vy,i+1 и ti+1:
vx,,i+1 = vx,,i+1/2 - 0.5 t’[2(0.5vi+1//22 - ri+1-1 - 0)si+1-3 ri+1-6xi+1 +
(1 + 2H0 + 2 ri+1 + ri+1-4)-0.5 ri+1-3xi+1],
vy,,i+1 = vy,,i+1/2 - 0.5 t’[2(0.5vi+1//22 - ri+1 -1 - 0)si+1-3 ri+1-6yi+1 +
(1 + 2H0 + 2 ri+1 + ri+1-4)-0.5 ri+1-3yi+1],
ti+1 = ti + 0.5 t’[(1 + 2H0 + 2 ri + ri -4)-0.5 + (1 + 2H0 + 2 ri+1 + ri+1 -4)-0.5].
64.
4”. В случае s = (1 + 2H0 + 2 r -1 + r -4)-0.5 уравнения для vx,i+1/2, vy,i+1/2, xi+1, yi+1 ,а также явные формулы для вычисления vx,i+1, vy,i+1 и ti+1 имеют вид:
vx,,i+1/2 = vx,,i - 0.5 t’[(0.5vi+1/22 - ri-1 - 0)(1 + 2H0 + 2 ri-1 + ri-4)-1(1 + 2 ri-3) + 1]
(1 + 2H0 + 2 ri-1 + ri-4)-0.5 ri-3xi,
vy,,i+1/2 = vy,,i - 0.5 t’[(0.5vi+1/22 - ri-1 - 0)(1 + 2H0 + 2 ri-1 + ri-4)-1(1 + 2 ri-3) + 1]
(1 + 2H0 + 2 ri-1 + ri-4)-0.5 ri-3yi,
xi+1= xi + 0.5 t’[(1 + 2H0 + 2 ri-1 + ri-4)-0.5 + (1 + 2H0 + 2 ri+1-1 + ri+1-4)-0.5]vx,,i+1/2,
yi+1= yi + 0.5 t’[(1 + 2H0 + 2 ri-1 + ri-4)-0.5 + (1 + 2H0 + 2 ri+1-1 + ri+1-4)-0.5]vy,,i+1/2 ;
vx,,i+1 = vx,,i+1/2 - 0.5 t’[2(0.5vi+1//22- ri+1-1- 0)(1+2H0+ 2 ri+1-1+ ri+1-4)-1(1+2 ri+1-3) +
1]
(1 + 2H0 + 2 ri+1-1 + ri+1-4)-0.5 ri+1-3xi+1,
vy,,i+1 = vy,,i+1/2 - 0.5 t’[2(0.5vi+1//22- ri+1-1- 0)(1+2H0+ 2 ri+1-1+ ri+1-4)-1(1+2 ri+1-3) +
1]
(1 + 2H0 + 2 ri+1 + ri+1-4)-0.5 ri+1-3yi+1,
ti+1 = ti + 0.5 t’[(1 + 2H0 + 2 ri-1 + ri-4)-0.5 + (1 + 2H0 + 2 ri+1-1 + ri+1-4)-0.5].
65.
4”. В случае si = (1 + 2H0 + 2 ri -1 + ri -4)-0.5 уравнения для vx,i+1/2, vy,i+1/2, xi+1, yi+1 ,а также явные формулы для вычисления vx,i+1, vy,i+1 и ti+1 имеют вид:
vx,,i+1/2 = vx,,i - 0.5 t’( Hi+1/2,isi2(1 + 2 ri-3) + 1)si ri-3xi,
vy,,i+1/2 = vy,,i - 0.5 t’( Hi+1/2,isi2(1 + 2 ri-3) + 1)si ri-3yi,
xi+1= xi + 0.5 t’(si + si+1)vx,,i+1/2, yi+1= yi + 0.5 t’(si + si+1)vy,,i+1/2 ;
vx,,i+1 = vx,,i+1/2 - 0.5 t’[ Hi+1/2,i+1si+12(1 + 2 ri+1-3) + 1]si+1 ri+1-3xi+1,
vy,,i+1 = vy,,i+1/2 - 0.5 t’[ Hi+1/2,i+1si+12(1 + 2 ri+1-3) + 1]si+1 ri+1-3yi+1,
ti+1 = ti + 0.5 t’(si + si+1).
Hi,j = 0.5vi2 - rj-1 - 0



























































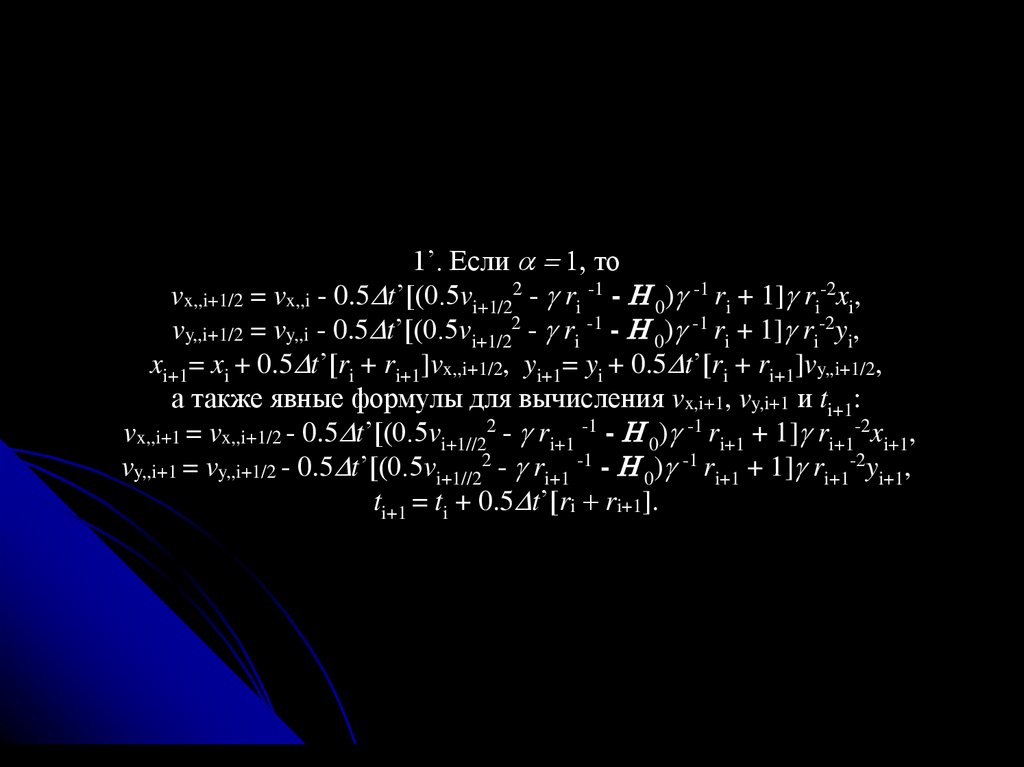




 mathematics
mathematics