Ряды динамики

1.

РЯДЫ ДИНАМИКИ

2.

• Ряд динамики – это числовые значения
статистических показателей,
изменяющихся во времени и расположенных
в хронологической последовательности.
Ряды динамики включают два обязательных
элемента:
1) период времени, за который или по
состоянию на который приводятся
цифровые значения ( показатель времени
t);
2) конкретные числовые значения показателя,
характеризующие изучаемый объект или
явление ( уровни ряда у)

3.

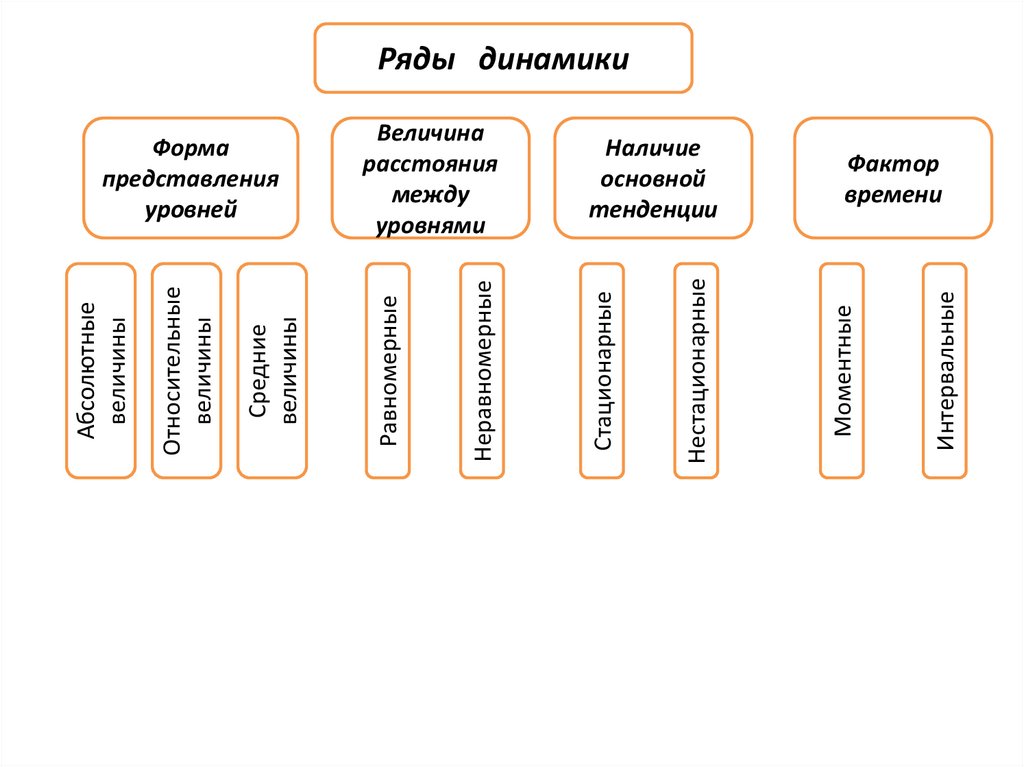
Интервальные
Наличие
основной
тенденции
Моментные
Нестационарные
Величина
расстояния
между
уровнями
Стационарные
Неравномерные
Форма
представления
уровней
Равномерные
Средние
величины
Относительные
величины
Абсолютные
величины
Ряды динамики
Фактор
времени

4.

• Моментные ряды динамики –
отображают состояние изучаемого
явления на определенную дату
времени.
Сумма уровней моментного ряда не имеет смысла.

5.

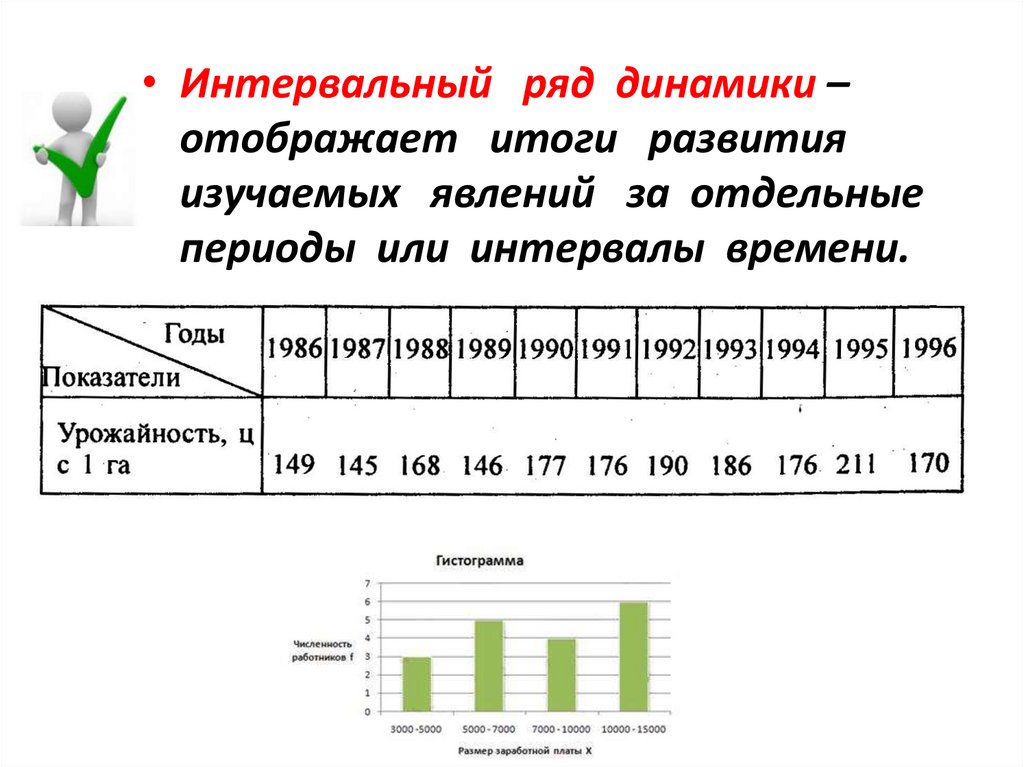
• Интервальный ряд динамики –
отображает итоги развития
изучаемых явлений за отдельные
периоды или интервалы времени.

6.

• Если уровни в интервальном ряду
выражены абсолютными показателями,
то их можно суммировать или дробить
во времени, получая новые числовые
значения объёма явления, относящиеся к
более крупным или мелким промежуткам
времени.
• Сумма уровней интервального ряда дает
вполне реальную статистическую
величину, называемую накопленные итоги
(например, общий объём налоговых
поступлений в госбюджет, общее
количество выпускников вузов и т.д.)

7.

Статистические данные должны быть
сопоставимы.
Основные требования сопоставимости
уровней рядов динамики:
одинаковая методология расчета
показателей для всех периодов (дат);
одинаковые и равноценные единицы
измерения;
одинаковость границ территории;
одинаковая полнота охвата различных
частей явления, представленного рядом
динамики.

8.

• Прежде чем анализировать ряд
динамики, необходимо, обеспечить
сопоставимость уровней ряда
дополнительными расчетами, т. е.
произвести так называемое смыкание
рядов динамики.
• Смыкание рядов динамики –
объединение в один динамический
ряд (более длинный) двух или
нескольких рядов, уровни которых
рассчитаны по разной методике
или в разных границах.

9.

Выделяют два способа смыкания рядов
динамики:
1) Расчет коэффициента пересчета
(коэффициент соотношения двух
уровней):
Умножая значения уровней ряда на этот
коэффициент, можно построить ряд
динамики сопоставимых уровней в новых
территориальных границах.

10.

2) Приведение рядов к одному основанию
(прием перехода от абсолютных
показателей к относительным) – уровни
всех рядов приводятся в процентах
(коэффициентах) к уровню одного и того
же периода или момента времени (или
иной базе сравнения).
В результате получают сомкнутый ряд.
• Динамический ряд не должен иметь
пропущенные уровни.
• В этом случае рекомендуется заполнять
такие пропуски условными расчетными
значениями.

11.

• Имеются данные об объёме производства и реализации
продукции организацией за последние 6 лет (млн. руб.).
На третьем году в организации произвели частичное
обновление оборудования.
Объём продукции
До реорганизации
После реорганизации
Годы
1
16,1
2
15,4
3
15,0
15,6
4
5
6
16,9
18,4
19,0
Приведём показатели ряда динамики к сопоставимому виду.
Решение: Приведём показатели ряда динамики к сопоставимому
виду, для этого определим коэффициент пересчёта k = 15,6/15,0 = 1,04 и
пересчитаем значения уровней для всех периодов, предшествующих
реорганизации, умножив их значение на k:
у1 16,1 1,04 16,74 _ млн. руб.;
у2 15,4 1,04 16,02 _ млн. руб.

12.

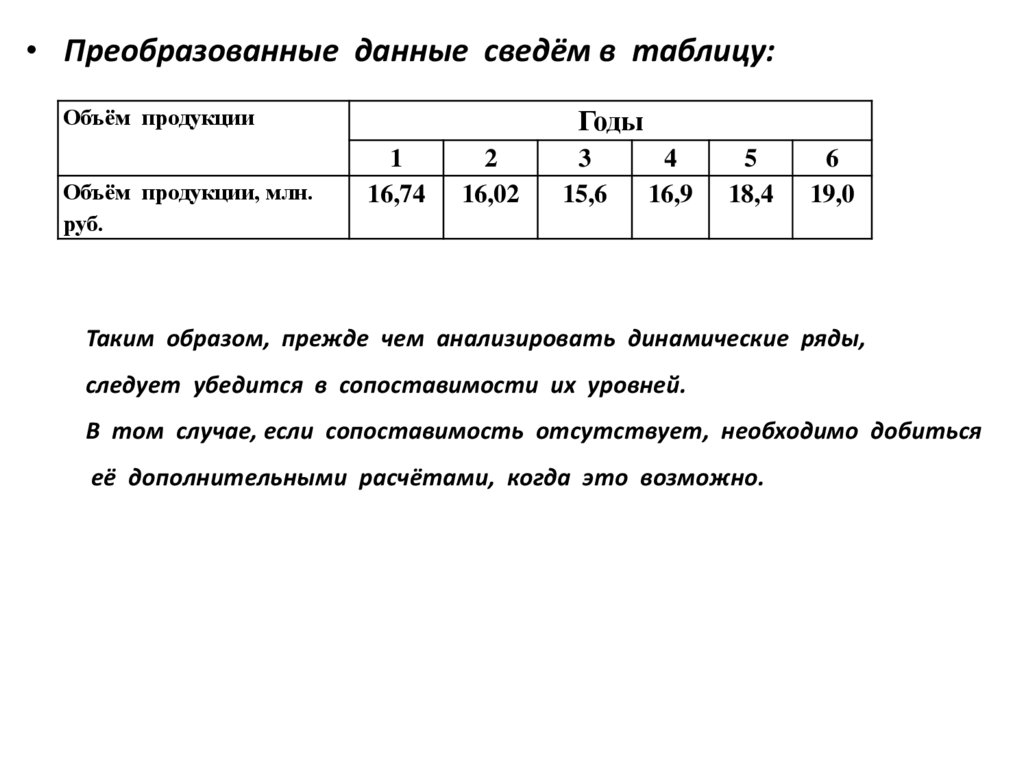
• Преобразованные данные сведём в таблицу:
Объём продукции
Объём продукции, млн.
руб.
Годы
1
16,74
2
16,02
3
15,6
4
16,9
5
18,4
6
19,0
Таким образом, прежде чем анализировать динамические ряды,
следует убедится в сопоставимости их уровней.
В том случае, если сопоставимость отсутствует, необходимо добиться
её дополнительными расчётами, когда это возможно.

13.

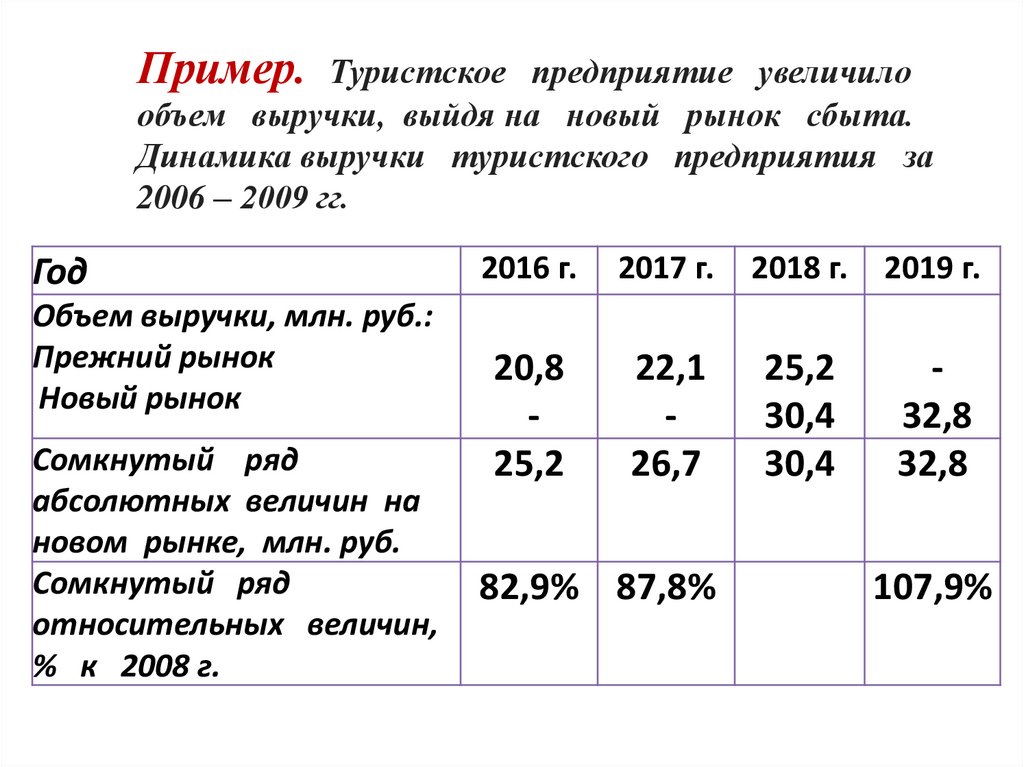
Пример. Туристское предприятие увеличило
объем выручки, выйдя на новый рынок сбыта.
Динамика выручки туристского предприятия за
2006 – 2009 гг.
Год
Объем выручки, млн. руб.:
Прежний рынок
Новый рынок
Сомкнутый ряд
абсолютных величин на
новом рынке, млн. руб.
Сомкнутый ряд
относительных величин,
% к 2008 г.
2016 г.
2017 г.
2018 г.
2019 г.
20,8
25,2
22,1
26,7
25,2
30,4
30,4
32,8
32,8
82,9% 87,8%
107,9%

14.

На основе данных 2008 г., определенных на две
даты, рассчитываем коэффициент пересчета:
2006 г.: 20,8 ∙ 1,21 = 25,2;
25,2 : 30,4 ∙ 100% = 82,9 %.
2007 г.: 22, 1 ∙ 1,21 = 26,7;
26,7 : 30,4 = 88 %.
2009 г.: 32,8 ∙ 1,21 = 39,7;
32,8 : 30,4 = 107,9 %
В итоге получаем сомкнутый (сопоставимый) ряд
динамики, отражающий объем выручки в
процентах к 2018 г.

15.

Валовой сбор овощей в районе, в пределах которого
возникли изменения (тыс. ц.)
Год
До изменения
2009 2010 2011
416 432 450
После изменения
630
k
1,4
450
-
-
y1 416 1,4 582
630
2012
-
2013
-
2014
-
622
648
684
y2 432 1,4 605
Валовой сбор овощей в новых границах района (тыс. ц.)
Год
В новых границах
2009
582
2010 2011 2012
605 630 622
2013
648
2014
684

16.

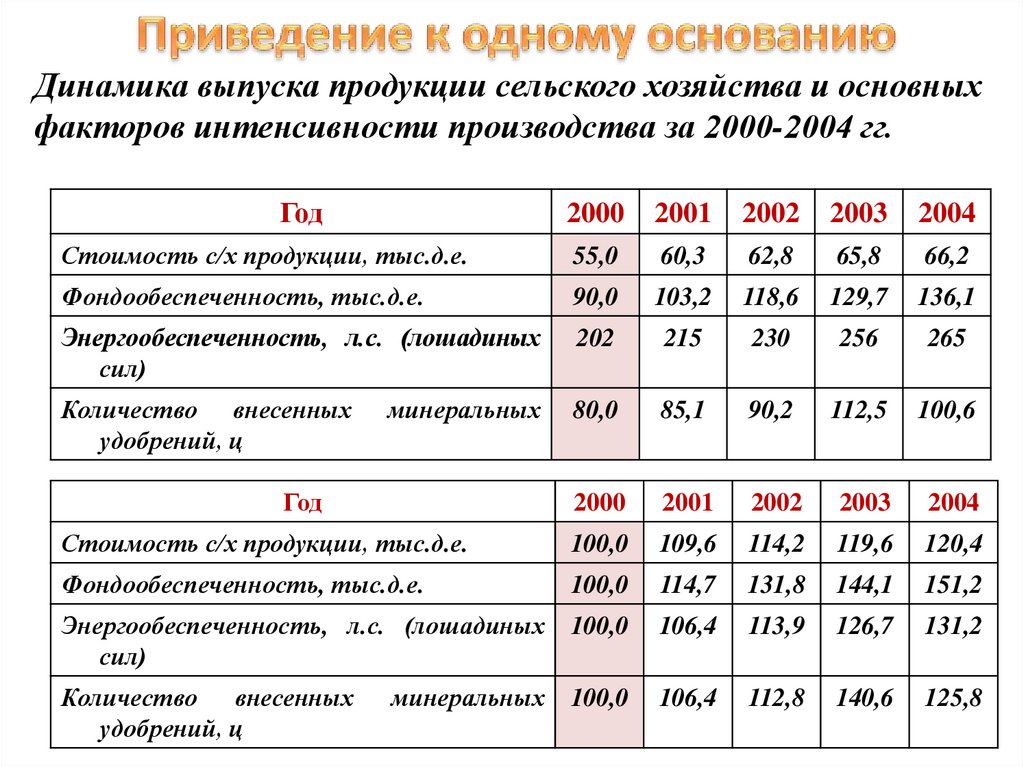
Динамика выпуска продукции сельского хозяйства и основных
факторов интенсивности производства за 2000-2004 гг.
Год
2000
2001
2002
2003
2004
Стоимость с/х продукции, тыс.д.е.
55,0
60,3
62,8
65,8
66,2
Фондообеспеченность, тыс.д.е.
90,0
103,2
118,6
129,7
136,1
Энергообеспеченность, л.с. (лошадиных
сил)
202
215
230
256
265
Количество внесенных
удобрений, ц
80,0
85,1
90,2
112,5
100,6
2000
2001
2002
2003
2004
Стоимость с/х продукции, тыс.д.е.
100,0
109,6
114,2
119,6
120,4
Фондообеспеченность, тыс.д.е.
100,0
114,7
131,8
144,1
151,2
Энергообеспеченность, л.с. (лошадиных
сил)
100,0
106,4
113,9
126,7
131,2
Количество внесенных
удобрений, ц
100,0
106,4
112,8
140,6
125,8
минеральных
Год
минеральных

17.

• Уровни динамического ряда имеют свойство
изменяться с различной скоростью и
интенсивностью.
• Для характеристика развития явления во
времени применяются специальные
статистические показатели.

18.

• Показатели анализа ряда динамики
могут рассчитываться на
постоянной и переменной базах
сравнения.
• Сравниваемый уровень – принято
называть отчётным;
• Уровень с которым производится
сравнение – называется базисным.

19.

• Для расчёта показателей на постоянной
базе каждый уровень сравнивается с
одним и тем же базисным уровнем.
• Рассчитанные показатели при этом
называются базисными.
• Для расчёта показателей на переменной
базе каждый последующий уровень
сравнивается с предыдущим.
• Рассчитанные показатели в этом случае
называются цепными.

20.

• Абсолютный прирост выражается в
натуральных единицах и показывает, на
сколько единиц изменился уровень ряда по
сравнению с базой.
Абсолютный прирост это расчетный
абсолютный показатель.

21.

Абсолютный прирост называется
базисным, если за базу сравнения
принят какой-либо определенный
уровень (чаще начальный)
yi yo ;
б
y
где yi уровень сравниваемого периода;
yо уровень базисного периода.

22.

Абсолютный прирост называется
цепным, если за базу сравнения принят
уровень предыдущего периода.
yi yi 1 ,
ц
y
где
yi уровень сравниваемого периода;
yi 1 уровень предшествующего периода.

23.

• Цепные и базисные абсолютные приросты
связаны между собой определенным
правилом: сумма последовательных цепных
абсолютных приростов равна последнему
базисному.
ц
у
б
у
• По знаку абсолютного прироста можно
сделать вывод о характере развития
явления:
у 0 рост,
у 0 спад,
у 0 стабильность.

24.

• Темп роста определяется как отношение двух
сравниваемых уровней и показывает, во сколько
раз данный уровень превышает уровень
базисного периода:
у1
• Базисный темп роста:
б
Тр
• Цепной темп роста:
уо
100%;
уi
Т
100%;
уi 1
ц
р
• Темп роста, выраженный в коэффициентах,
принято называть коэффициентами роста:
• Темп роста всегда
число.
Т р положительное
К р 100%;

25.

• Темп прироста или темп сокращения (темп
изменения уровней) показывает, на сколько
процентов уровень данного периода больше
или меньше определенного уровня и
характеризует относительную скорость
изменения уровня ряда в единицу времени.

26.

Темп прироста можно рассчитать двумя
способами:
1) Как отношение абсолютного прироста к
уровню:
б
у
yi y o
у
б
Т
100
%
100%;
Базисного:
пр
yo
уо
ц
у
yi yi 1
у
ц
100%
100%;
Цепной: Т пр
yi 1
уi 1
2) Как разность между темпом роста и 100%:
Т пр Т р 100%.

27.

Между базисными и цепными показателями
существует взаимосвязь:
1) Сумма цепных абсолютных приростов равна
базисному приросту;
2) Произведение цепных коэффициентов роста
равно базисному;
3) Деление рядом стоящих базисных
коэффициентов роста друг на друга равно
цепным коэффициентам роста.

28.

• Темп наращивания рассчитывается делением
цепных абсолютных приростов на уровень,
принятый за постоянную базу сравнения.
yi yi 1
Тн
100%
100%.
yo
уо
ц
y

29.

• Чтобы знать, что скрывается за каждым
процентом прироста, рассчитывается
абсолютное значение 1% прироста как
отношение абсолютного прироста уровня за
интервал времени к темпу прироста за тот
же промежуток времени:
yi yi 1
А%
yi yi 1
yi 1
или
А%
ц
у
Т пр

30.

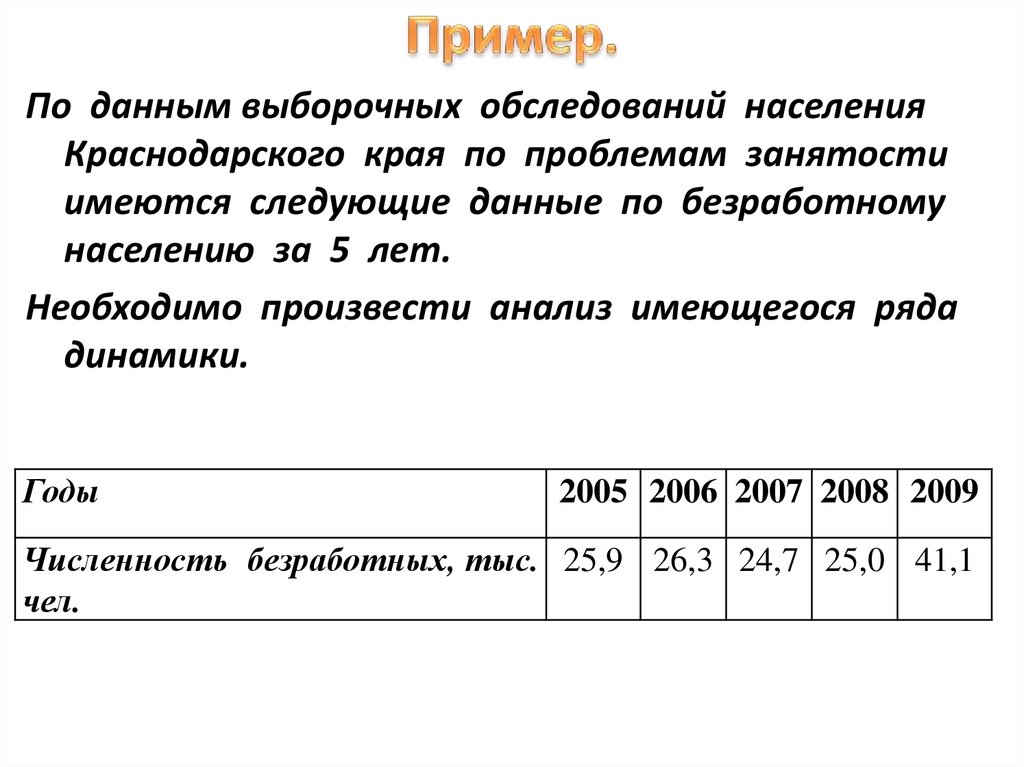
По данным выборочных обследований населения
Краснодарского края по проблемам занятости
имеются следующие данные по безработному
населению за 5 лет.
Необходимо произвести анализ имеющегося ряда
динамики.
Годы
2005 2006 2007 2008 2009
Численность безработных, тыс. 25,9 26,3 24,7 25,0 41,1
чел.

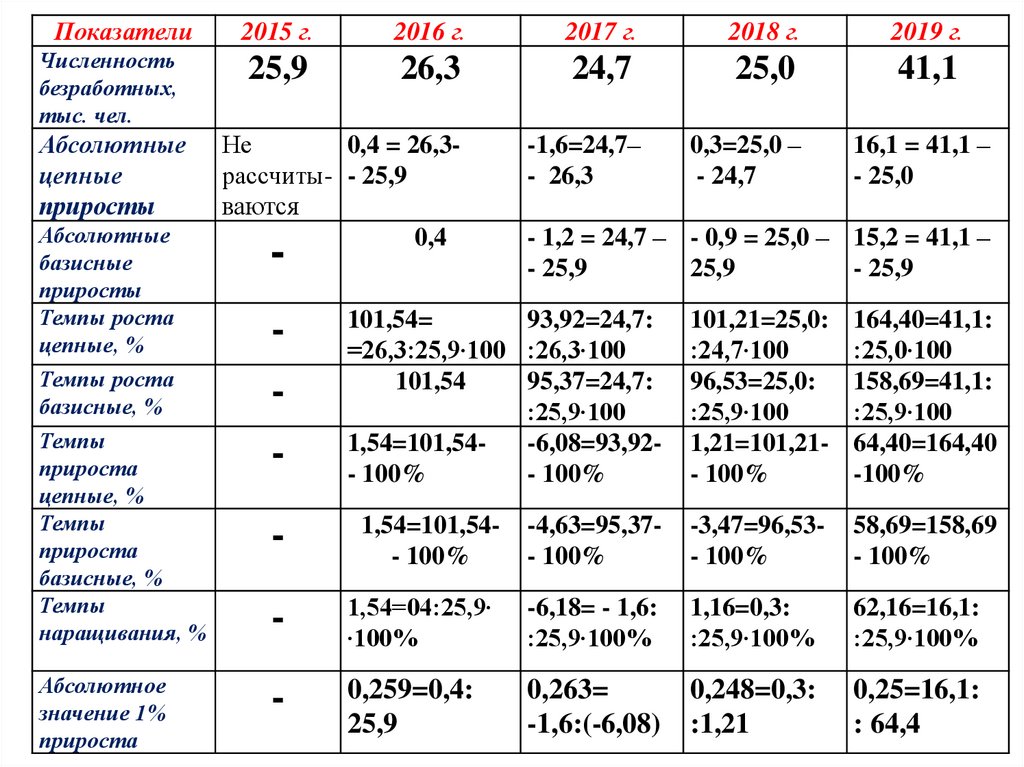
31.

Показатели
2015 г.
2016 г.
2017 г.
2018 г.
2019 г.
Численность
безработных,
тыс. чел.
25,9
26,3
24,7
25,0
41,1
Не
0,4 = 26,3рассчиты- - 25,9
ваются
0,4
-1,6=24,7–
- 26,3
0,3=25,0 –
- 24,7
Абсолютные
цепные
приросты
Абсолютные
базисные
приросты
Темпы роста
цепные, %
-
16,1 = 41,1 –
- 25,0
- 1,2 = 24,7 – - 0,9 = 25,0 – 15,2 = 41,1 –
- 25,9
25,9
- 25,9
101,54=
93,92=24,7:
=26,3:25,9∙100 :26,3∙100
101,54
95,37=24,7:
:25,9∙100
1,54=101,54-6,08=93,92- 100%
- 100%
101,21=25,0:
:24,7∙100
96,53=25,0:
:25,9∙100
1,21=101,21- 100%
164,40=41,1:
:25,0∙100
158,69=41,1:
:25,9∙100
64,40=164,40
-100%
-
1,54=101,54- 100%
-4,63=95,37- 100%
-3,47=96,53- 100%
58,69=158,69
- 100%
-
Темпы роста
базисные, %
-
Темпы
прироста
цепные, %
Темпы
прироста
базисные, %
Темпы
наращивания, %
-
-
1,54=04:25,9∙
∙100%
-6,18= - 1,6:
:25,9∙100%
1,16=0,3:
:25,9∙100%
62,16=16,1:
:25,9∙100%
Абсолютное
значение 1%
прироста
-
0,259=0,4:
25,9
0,263=
-1,6:(-6,08)
0,248=0,3:
:1,21
0,25=16,1:
: 64,4

32.

Вывод: в Краснодарском крае наблюдается
неблагоприятная ситуация среди безработного
населения, проявляющаяся в увеличении значений
основных показателей динамики.
Наибольший прирост безработных произошел в
2009 г. и составил 15,2 тыс, чел., или 58,69%, по
сравнению с 2005 г., что объясняется влиянием
экономического кризиса на ситуацию занятости.
Снижение показателей динамики наблюдается
только в 2007 г. по сравнению с 2006 г. на 1,6 тыс.
чел., а темп снижения составил 6,08%, или 4,63%
по базису.

33.

Система средних показателей динамики в
включает:
• Средний уровень ряда;
• Средний абсолютный прирост;
• Средний темп роста;
• Средний темп прироста.

34.

Средний уровень ряда динамики ( y ) –
рассчитывается по средней хронологической.
Средней хронологической называется средняя,
исчисленная из значений, изменяющихся во
времени.
Для интервальных рядов с равноотстоящими
уровнями средний уровень находится по
формуле средней арифметической простой, а
для неравноотстоящих уровней - по средней
арифметической взвешенной:
y
y
;y
n
yt
t
где y - уровень ряда динамики;
n - число уровней ряда;
t – число периодов времени, в
течение которых уровень не изменялся.

35.

• Средний темп роста это свободная
обобщающая характеристика интенсивности
изменения уровней ряда динамики,
показывающая, во сколько раз в среднем за
единицу времени изменился уровень
динамического ряда.
T p К1 К 2 ... К n
m
yn
T p n 1
y0
где m – число коэффициентов
роста.

36.

Средний темп прироста (%)
определяется по единственной
методологии:
Тпр Тр 100

37.

Средний уровень моментного равноотстоящего
ряда динамики находится по формуле средней
хронологической:
1 / 2 y1 y 2 y3 ... 1 / 2 y n
y
n 1
Средний уровень моментных рядов динамики с
неравноотстоящими уровнями определяется
средней хронологической взвешенной:
y
y1 y 2 t1 y 2 y3 t 2 ... y n 1 y n t n 1
2 t i
где yi; yn – уровни рядов динамики;
ti – длительность интервала времени между
уровнями

38.

Средний абсолютный прирост ( ) является
обобщающим показателем скорости изменения
явления во времени.
Он рассчитывается по формулам в
зависимости от способа нумерации
интервалов (моментов).
y n y0
;
n 1
n 1
цеп