Similar presentations:
Скалярное и векторное произведение
1.
Математика в GameDevСкалярное и векторное произведение
Векторы
Интегралы
Отражение, матрицы
Скалярные манипуляции
Косинус, синус, тангенс...
2.
Игры тесно связаны сматематикой, начиная от
геймдизайна и программирования
игровых механик до создания и
оптимизации графики и звукового
оформления. В этом докладе
рассматривается важность
математики в игровой индустрии,
приводятся примеры
использования различных
математических концепций в
процессе разработки игр и
исследуются специфические
алгоритмы и методы, применяемые
в данной области.
3.
Векторная математика.Векторы и векторная математика являются
необходимыми инструментами для разработки игр.
Многие операции и действия завязаны на ней
целиком.
4.
Интегралы.У интегралов очень много
применений, таких как: физические
симуляции, VFX(Визуальные
эффекты), аналитика и многое
другое.
5.
Некоторые вещи, которыеполностью опираются на
математику:
Симуляция жидкостей
Анимация
Алгоритмы
Архитектура игровых движков
Написание игровой логики
Аналитика и сбор данных
Расчёт кадров в секунду
Игровая физика
Графика/Шейдеры
Искуственный интеллект
Процедурная генерация
Рендеринг полигонов
И много другого...
6.
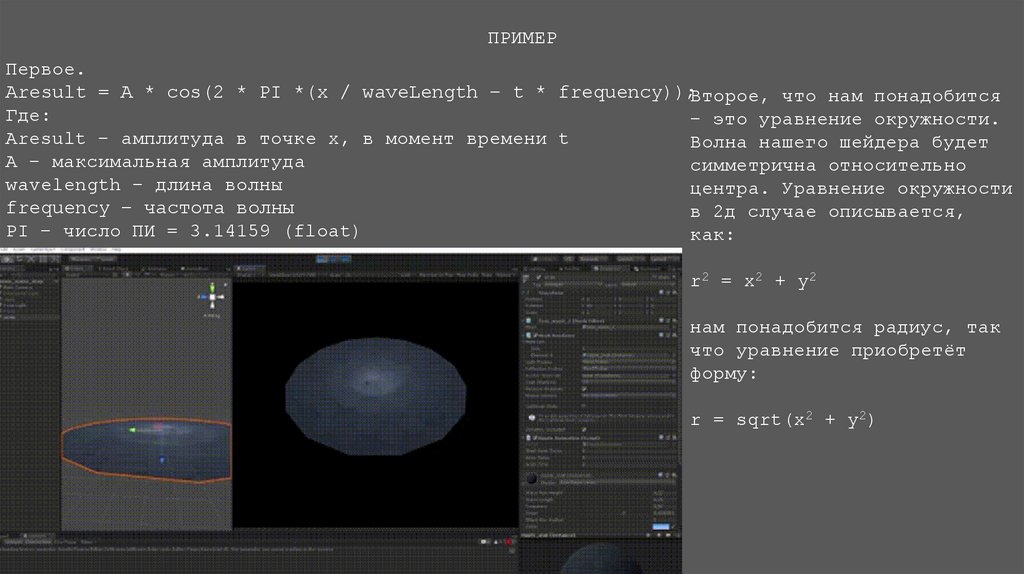
ПРИМЕРПервое.
Aresult = A * cos(2 * PI *(x / waveLength – t * frequency));Второе, что нам понадобится
Где:
– это уравнение окружности.
Aresult – амплитуда в точке x, в момент времени t
Волна нашего шейдера будет
А – максимальная амплитуда
симметрична относительно
wavelength – длина волны
центра. Уравнение окружности
frequency – частота волны
в 2д случае описывается,
PI – число ПИ = 3.14159 (float)
как:
r2 = x2 + y2
нам понадобится радиус, так
что уравнение приобретёт
форму:
r = sqrt(x2 + y2)






 mathematics
mathematics








