Similar presentations:
Математическое ожидание и его свойство
1.
МАТЕМАТИЧЕСКОЕОЖИДАНИЕ
И ЕГО СВОЙСТВО
2.
Пусть Х - дискретная случайнаявеличина,
заданная
своим
рядом
распределения:
x1
…
xi
…
xn
p1
…
pi
…
pn
3.
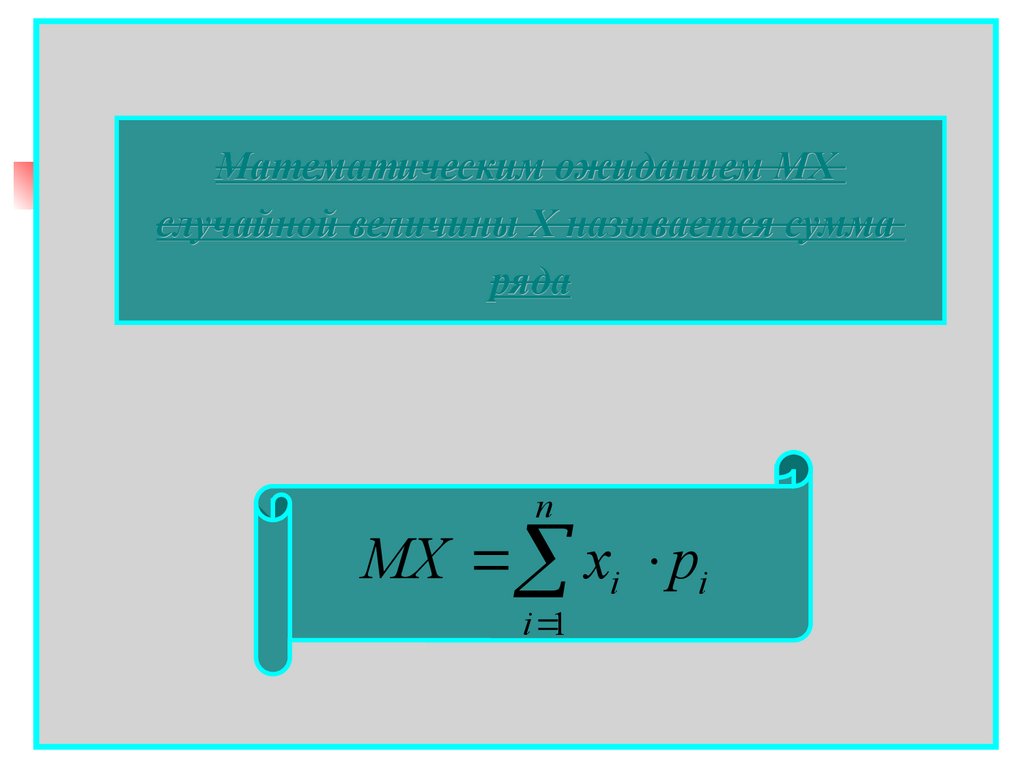
Математическим ожиданием MXслучайной величины Х называется сумма
ряда
n
MX xi pi
i 1
4.
Пример Х –число очков приоднократном бросании игральной
кости МХ-?
5.
Среднее арифметическое значений,принимаемых случайной величиной в
длинной серии опытов, приближенно
равно ее математическому ожиданию.
6.
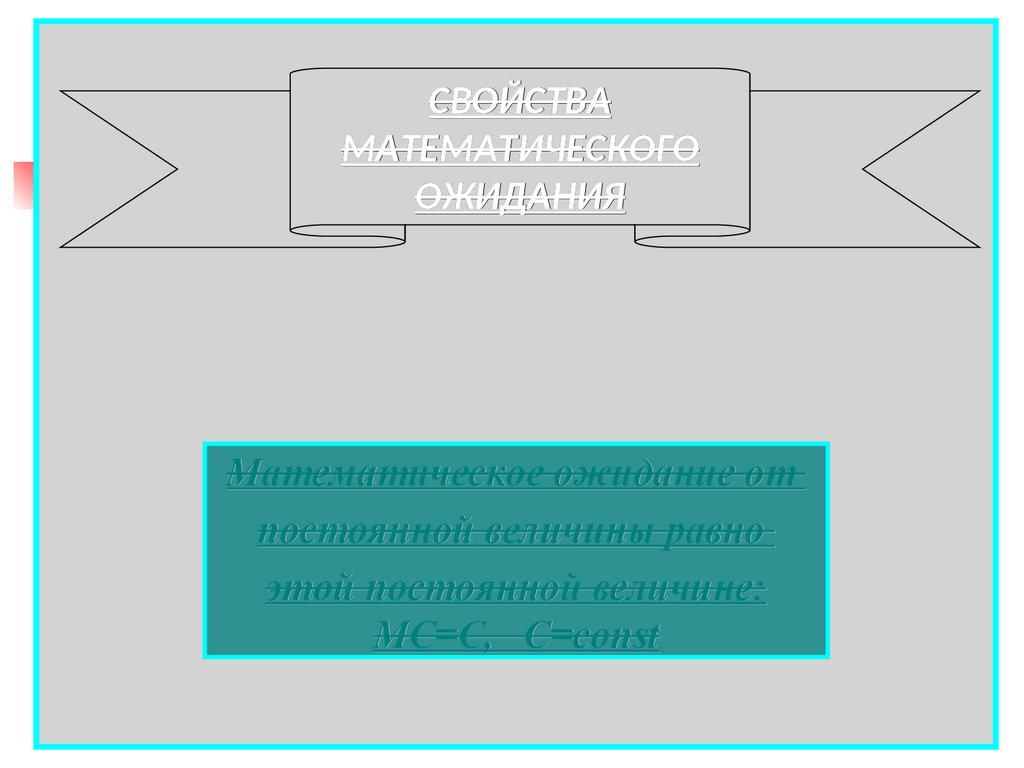
СВОЙСТВАМАТЕМАТИЧЕСКОГО
ОЖИДАНИЯ
Математическое ожидание от
постоянной величины равно
этой постоянной величине:
МC=C, C=const
7.
Математическое ожидание суммыслучайных величин Х и У равно
сумме математических ожиданий
этих величин:
М(X+Y)=MX+MY
8.
Постоянную величину можновыносить за знак математического
ожидания:
М(с X)=с MX, где с=cоnst.
9.
Математическое ожиданиепроизведения
независимых случайных величин
Х и Y равно произведению
математических ожиданий этих
величин:
М(XY)=MX MY







 mathematics
mathematics








