Similar presentations:
Матрицы и действия с ними
1. Матрицы и действия с ними
2.
Матрица. Определение3.
Нулевая, квадратная матрицы. Главная диагональ квадратнойматрицы
4.
Единичная матрица. Матрица-вектор.5.
Транспонированная матрица.6.
Свойства транспонированной матрицы. Симметрическая(симметричная) матрица.
7.
Сложение матриц. Умножение на действительное число8.
Свойства операций суммирования и умножения надействительное число.
9.
Скалярное произведение векторов.Ранее, матрицей – вектором, мы называли матрицу, состоящую
только из одной строки или только из одного столбца. Назовем
элементы такой матрицы координатами вектора, тогда:
10.
Умножение матриц.11.
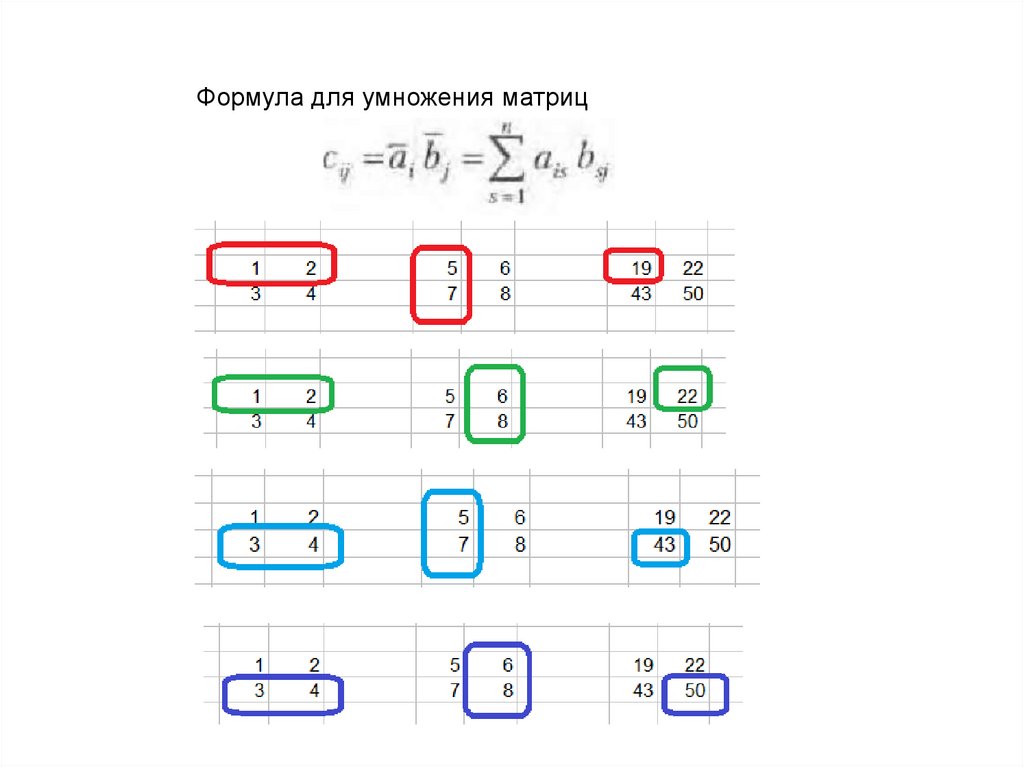
Формула для умножения матриц12.
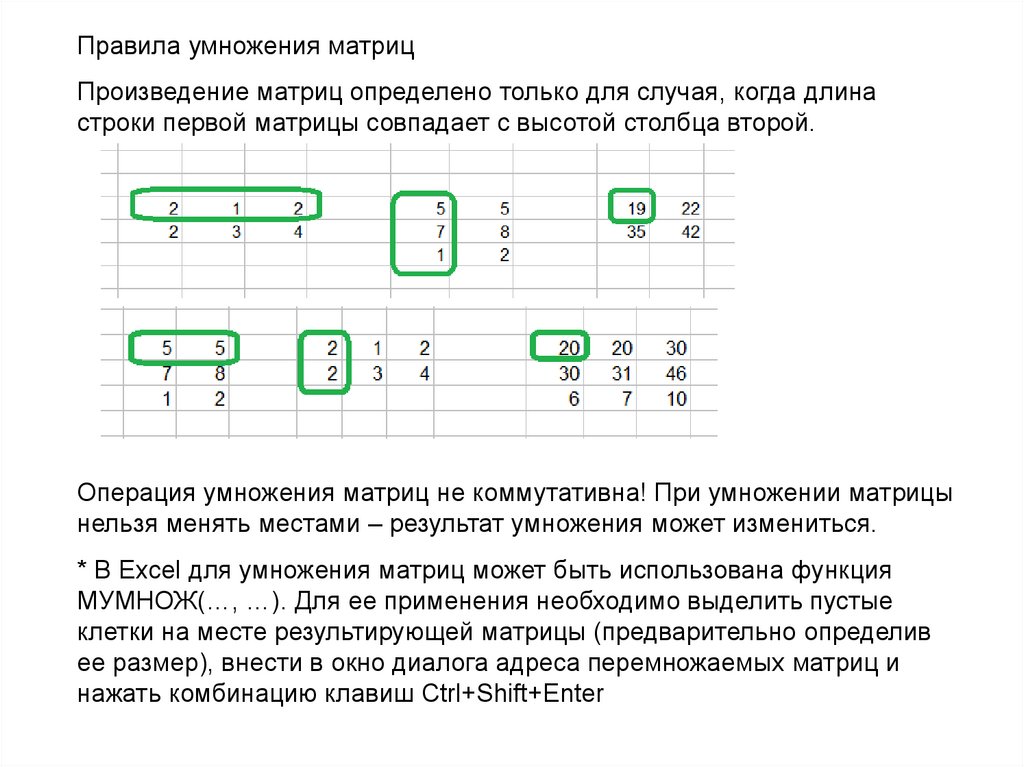
Правила умножения матрицПроизведение матриц определено только для случая, когда длина
строки первой матрицы совпадает с высотой столбца второй.
Операция умножения матриц не коммутативна! При умножении матрицы
нельзя менять местами – результат умножения может измениться.
* В Excel для умножения матриц может быть использована функция
МУМНОЖ(…, …). Для ее применения необходимо выделить пустые
клетки на месте результирующей матрицы (предварительно определив
ее размер), внести в окно диалога адреса перемножаемых матриц и
нажать комбинацию клавиш Ctrl+Shift+Enter
13.
Свойства произведения матриц.14.
Матрицы элементарных преобразований15.
Матрицы элементарных преобразований (2).16.
Матрицы элементарных преобразований (3).17.
Арифметические операции над строками матрицы.18.
Элементарные преобразования.19.
Преобразование матрицы к единичному видуОбратите внимание!
К единичному виду может быть преобразована только квадратная
матрица, причем только при выполнении определенных условий,
наложенных на ее значения, которые позволяют называть такую
матрицу невырожденной.
20.
Порядок преобразования матрицы к единичному виду.21.
Пример получения единичной матрицы с помощьюэлементарных преобразований.
22.
Вычисление обратной матрицы с помощью элементарныхпреобразований.
Пусть используя матрицы элементарных преобразований мы получили
единичную матрицу, то есть можем записать выражение:
Отсюда получим:
23.
.24. Определители матриц
25.
Понятие определителя. Упорядоченные наборы элементов26.
Понятие определителя. Инверсия в перестановках номеровстолбцов
27.
Понятие определителя. Определение28.
Определители первого и второго порядка.29.
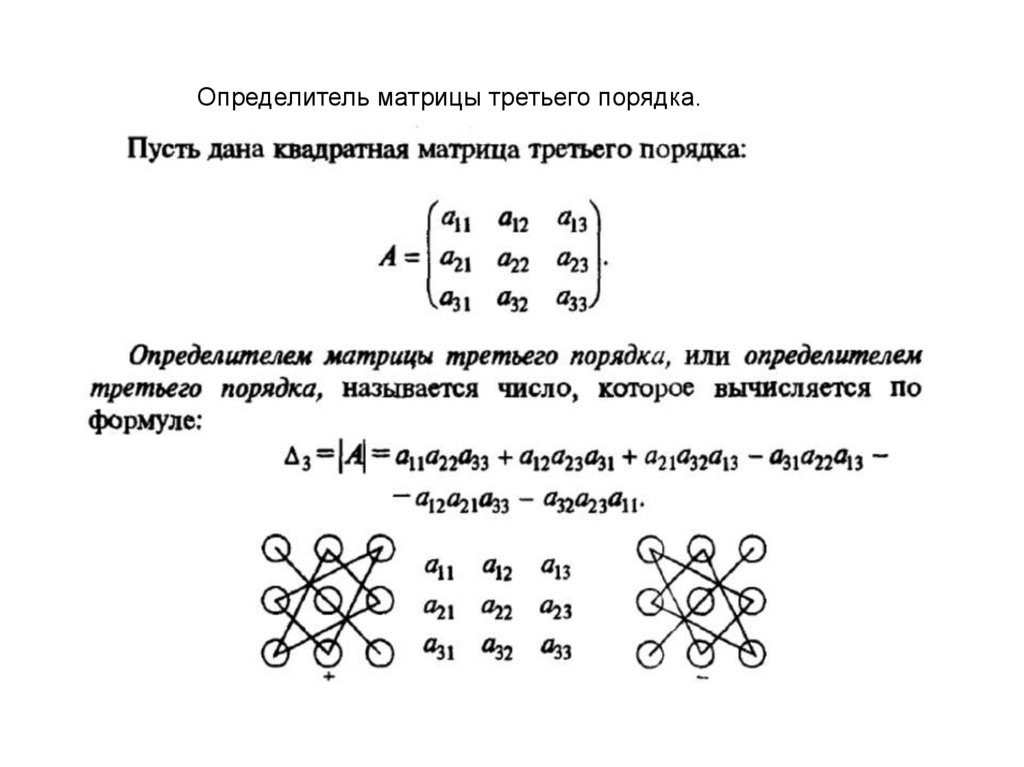
Определитель матрицы третьего порядка.30.
Минор элемента матрицы.31.
Алгебраическое дополнение элемента матрицы.32.
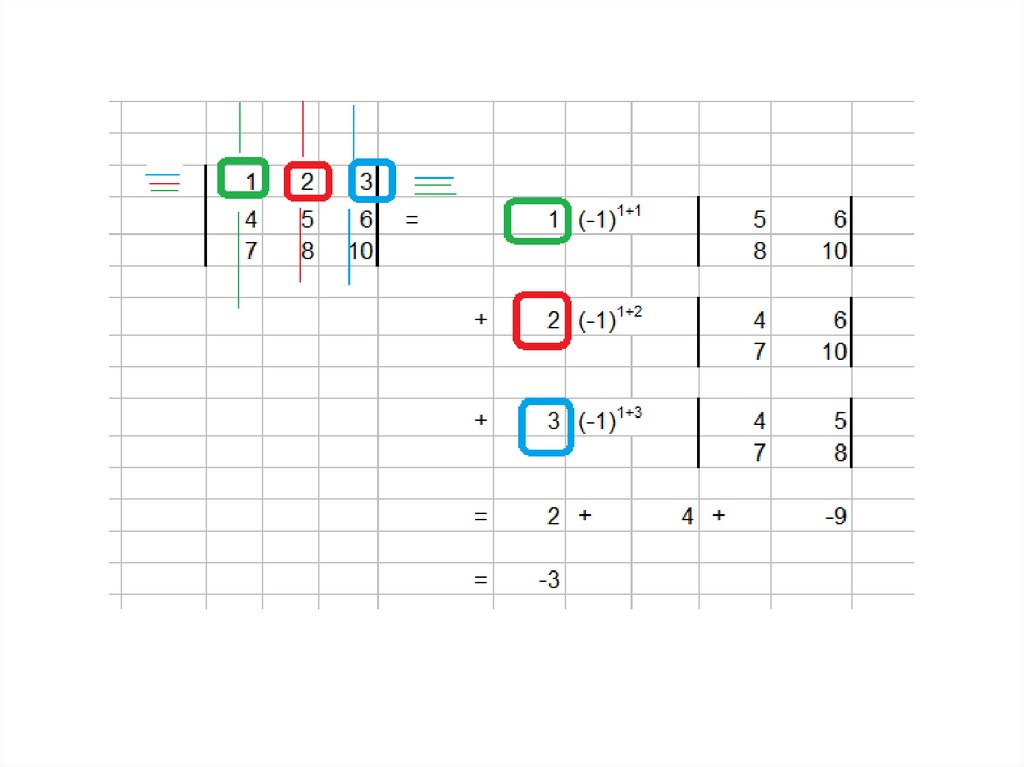
Теорема Лапласа.33.
34.
Общие свойства определителей.35.
.36.
В Excel определитель матрицы может быть вычислен спомощью функции МОПРЕД (…)
.
37.
Вычисление обратной матрицы с помощью определителя.38.
В Excel обратная матрица вычисляется с помощью функцииМОБР(…).
39.
Ранг матрицы.40.
.41.
.42.
Определение ранга путем преобразования матрицы кступенчатому виду
Чему равен ранг матрицы А?
43.
Линейная зависимость строк (столбцов) матрицы.44.
Связь между линейной зависимостью строк (столбцов) матрицыи ее рангом.
Если какая-то из строк матрицы является линейной
комбинацией остальных, с помощью элементарных преобразований
третьего типа мы можем получить из исходной матрицы матрицу с
нулевой строкой. Определитель такой матрицы равен 0, и, в то же
время, равен определителю исходной матрицы.
Матрица называется невырожденной, когда ее строки (столбцы)
линейно независимы.
Матрица вырождена, когда ее строки (столбцы) линейно зависимы.
Определитель вырожденной матрицы равен 0.








































 mathematics
mathematics








