Similar presentations:
Формулы для математического ожидания и дисперсии случайных величин “число успехов” и “частота успеха”
1.
Вероятностьи статистика
9 класс
2.
ОТВЕТЬТЕ НА ВОПРОСЫ:1. Запишите формулы для математического
ожидания
и
дисперсии случайных величин “число успехов” и
“частота успеха” в серии из n испытаний Бернулли с
вероятностью успеха p.
2.
Проводятся две серии испытаний Бернулли длины n.
Вероятность успеха в первой серии равна 0,2, а во второй
вероятность успеха равна 0,8. Не производя вычислений,
сравните:
а) математическое ожидание числа успехов в первой и во
второй серии;
б) дисперсия числа успехов в первой и во второй серии.
3.
ОТВЕТЬТЕ НА ВОПРОСЫ:Чему
равно
ожидаемое
число
успехов
S
при
вероятности
3.
успеха 0,5 в серии из 20 испытаний?
ES = np = 20 ∙ 0,5 = 10
Проведите такой эксперимент: подбросьте 20
раз монету, считая успехом выпадение орла.
Подсчитайте число наступивших успехов.
Совпало ли число успехов с ожидаемым
значением? Сильно ли оно отличается от
ожидаемого значения?
4.
ОТВЕТЬТЕ НА ВОПРОСЫ:Производится
серия
испытаний
4.
Бернулли.
Выберите верное утверждение:
а) чем больше вероятность успеха, тем больше
математическое ожидание числа неудач;
б) чем больше вероятность успеха, тем меньше
математическое ожидание числа неудач;
в) среднее число успехов зависит только от числа
экспериментов и не связано с вероятностью
успеха.
5.
проверкадомашнего
задания
6.
№2
По полу рассыпали содержимое коробки, в
которой было 100 канцелярских кнопок.
Каково математическое ожидание числа
“опасных” кнопок, лежащих остриём вверх,
если вероятность попадания кнопки остриём
вверх равна 0,45?
Решение:
ES = np = 100 ∙ 0,45 = 45
7.
№2
Игральную кость бросили 120 раз. Найдите
математическое
ожидание
случайной
величины:
а) “выпавшее число очков делится на 3”;
б) “выпала пятёрка”.
Решение:
а) Из всех возможных вариантов только 2
числа делятся на 3:
1, 2, 3, 4, 5, 6
8.
№2
2
1
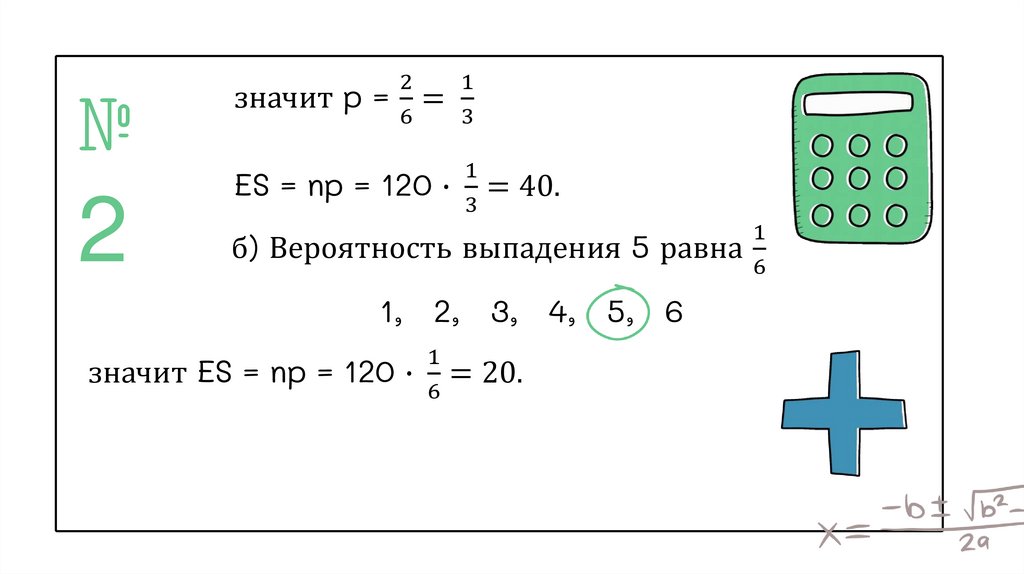
значит p = =
6
3
1
ES = np = 120 ∙ = 40.
3
1
б) Вероятность выпадения 5 равна
6
1, 2, 3, 4, 5, 6
1
значит ES = np = 120 ∙ = 20.
6
9.
В тексте из 16 задач каждая задача имеет 4варианта ответов, но только один ответ из
четырёх верный. Миша не готов к тесту и
выбирает ответы наугад. Найдите ожидаемое
число правильных ответов, которые Миша
угадал.
№
2
Решение:
n = 16
1
p=
4
1
ES = np = 16 ∙ = 4.
4
10.
№2
По полу рассыпали содержимое коробки, в
которой было 100 канцелярских кнопок.
Кнопка падает остриём вверх с вероятностью
0,36. Найдите дисперсию и стандартное
отклонение
величины
“число
кнопок,
упавших остриём вверх”.
Решение:
n = 100
p = 0,36
q = 0,64
DS = npq = 100 ∙ 0,36 ∙ 0,64 = 23,04



















 mathematics
mathematics








