Сумма углов треугольника. Урок геометрии в 7 классе

1.

Урок геометрии
в 7 классе
«Сумма углов треугольника»

2.

В жизни треугольники встречается повсюду: при
строительстве домов, мостов и других сооружений

3.

В
1. Элементы треугольника
А, В, С – вершины треугольника.
АВ, АС, ВС – стороны треугольника.
С
< А, < В, < С – углы треугольника .
А
М
В
2. Отрезки, которые можно провести в
треугольнике: Д
А
С
С
СМ- биссектриса
К
Р
СР - медиана
N
Е
С
К
ДК - высота

4.

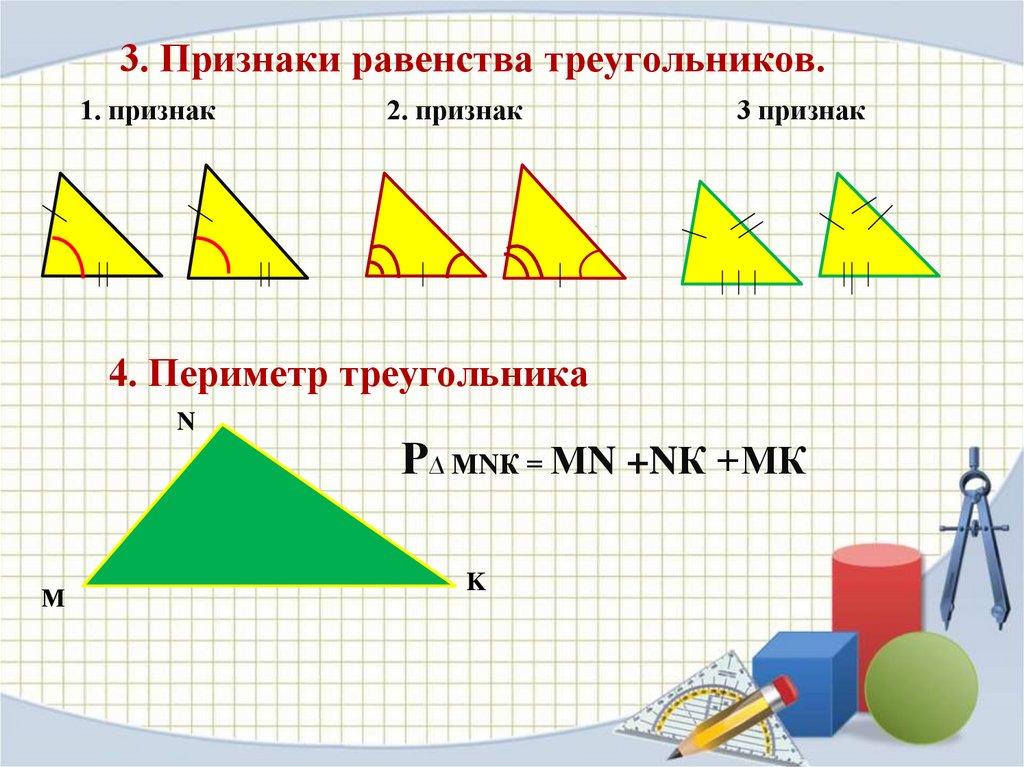
3. Признаки равенства треугольников.
1. признак
2. признак
3 признак
4. Периметр треугольника
N
М
Р∆ МNК = МN +NК +МК
K

5.

Задача 1
Дано: ∆АВС, АВ=20см
АС=15см, Р∆АВС=60см
А
Найти: ВС
В
ВС=60-20-15=25 см
С
Задача 2.
К
Дано: ∆ МКР, < М = 30°
М
Р
< К= 100°
Найти: < Р

6.

Назовите углы, образованные при пересечении двух прямых
третьей прямой.
< 1и < 3,
2
7
8
4
3
5
6
< 2 и < 4, < 7 и < 5, < 8 и <6
соответственные углы
< 7 и < 4, < 8 и < 3
накрест лежащие углы
< 7 и < 3, < 8 и < 4
односторонние углы

7.

Продолжите предложение: если две параллельные
прямые пересечены секущей, то…
1. соответственные углы равны
2. сумма односторонних углов равна 180°
3. накрест лежащие углы равны
2. В каком треугольнике углы при основании
равны?
в равнобедренном

8.

• В.Ф. Коган сказал: «Легче остановить
Солнце. Легче сдвинуть Землю, чем
уменьшить сумму углов
треугольника».
• Свойство суммы углов треугольника
было открыто эмпирически, т. е.
опытным путем еще в Древнем Египте.
Однако дошедшие до нас сведения
относятся к более позднему времени.
Древнегреческий ученый Прокл (410585г.г. н.э.) утверждал, комментируя
книгу « Начала» Евклида, что согласно
Евдему Родосскому (сумма углов
треугольника равна развернутому
углу.)

9.

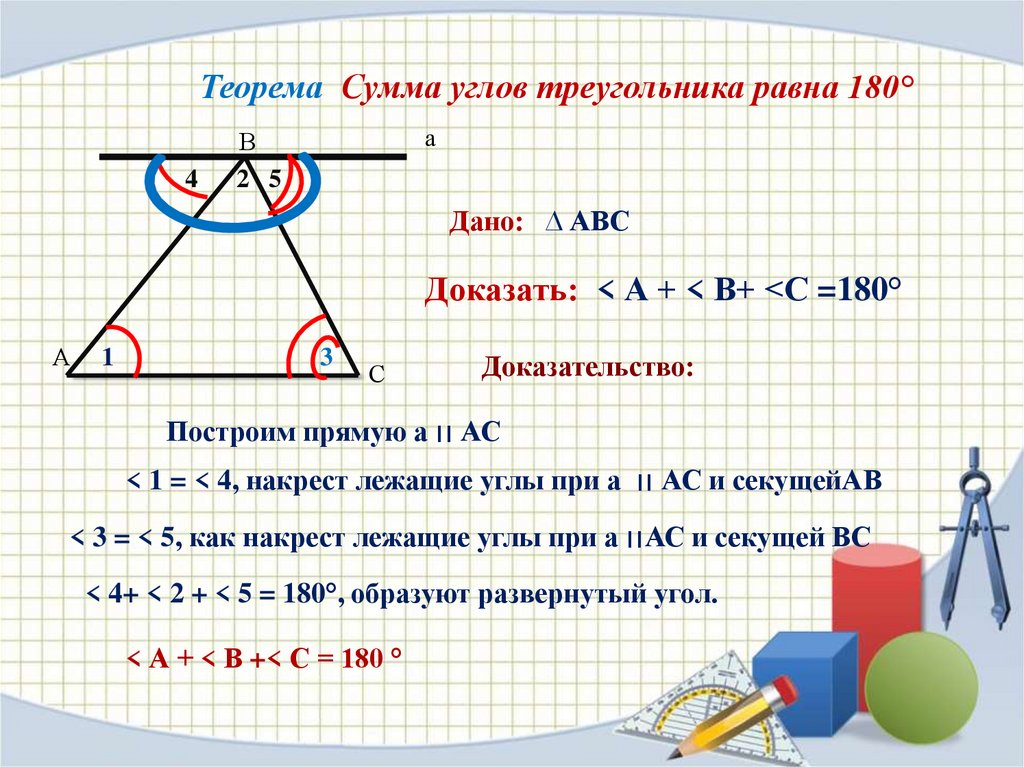
Теорема Сумма углов треугольника равна 180°
4
а
В
2 5
Дано: ∆ АВС
Доказать: < А + < В+ <С =180°
А
1
3
С
Доказательство:
Построим прямую а ‫ ׀׀‬АС
< 1 = < 4, накрест лежащие углы при а ‫ ׀׀‬АС и секущейАВ
< 3 = < 5, как накрест лежащие углы при а ‫׀׀‬АС и секущей ВС
< 4+ < 2 + < 5 = 180°, образуют развернутый угол.
< А + < В +< С = 180 °

10.

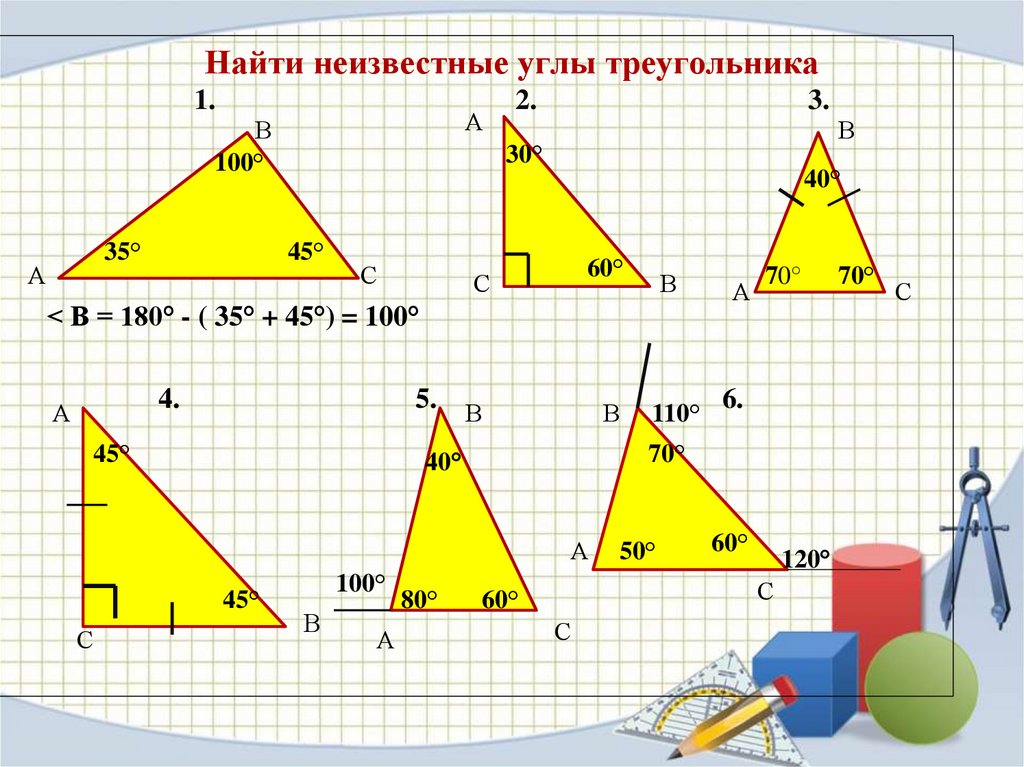
Найти неизвестные углы треугольника
1.
А
В
100°
35°
А
2.
3.
В
30°
40°
45°
С
С
60°
В
В
110°
< В = 180° - ( 35° + 45°) = 100°
4.
А
5.
45°
В
А
С
100°
В
А
80°
70°
6.
70°
40°
45°
А
50°
60°
120°
С
60°
С
70°
С

11.

12.

Установите соответствие между сторонами и углами
треугольников
Треугольник
Прямоугольный
Остроугольный
Тупоугольный
Градусные меры углов
10°,
45°,
30°,
30°,
140°
55°, 80°
60°,
90°

13.

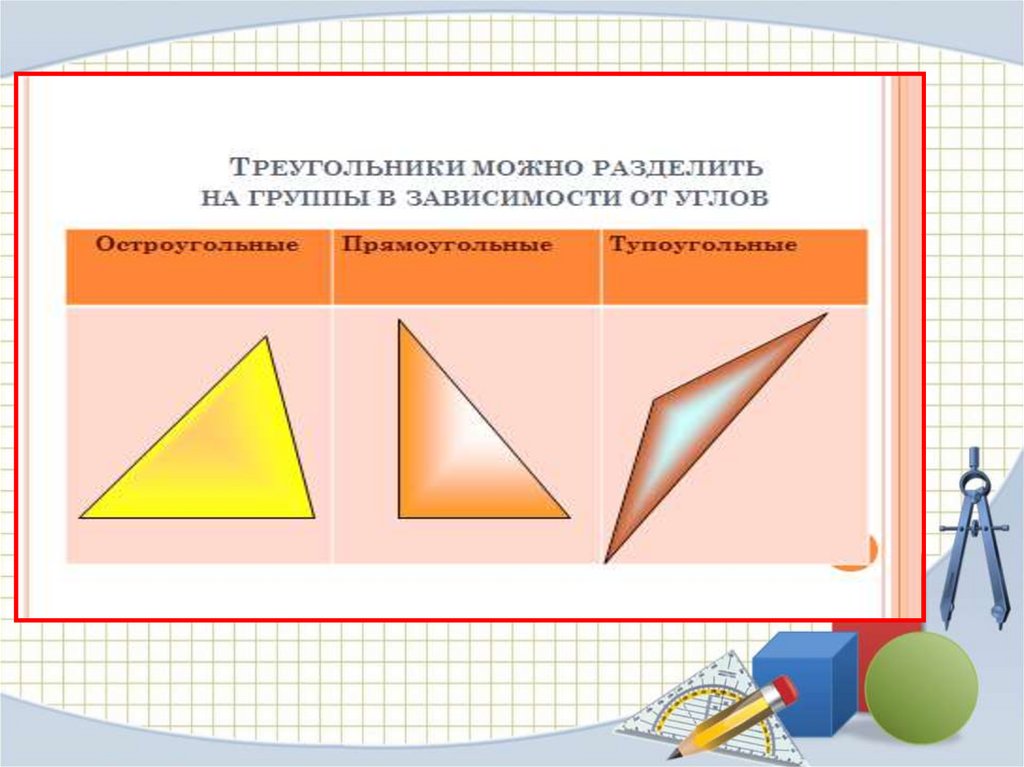
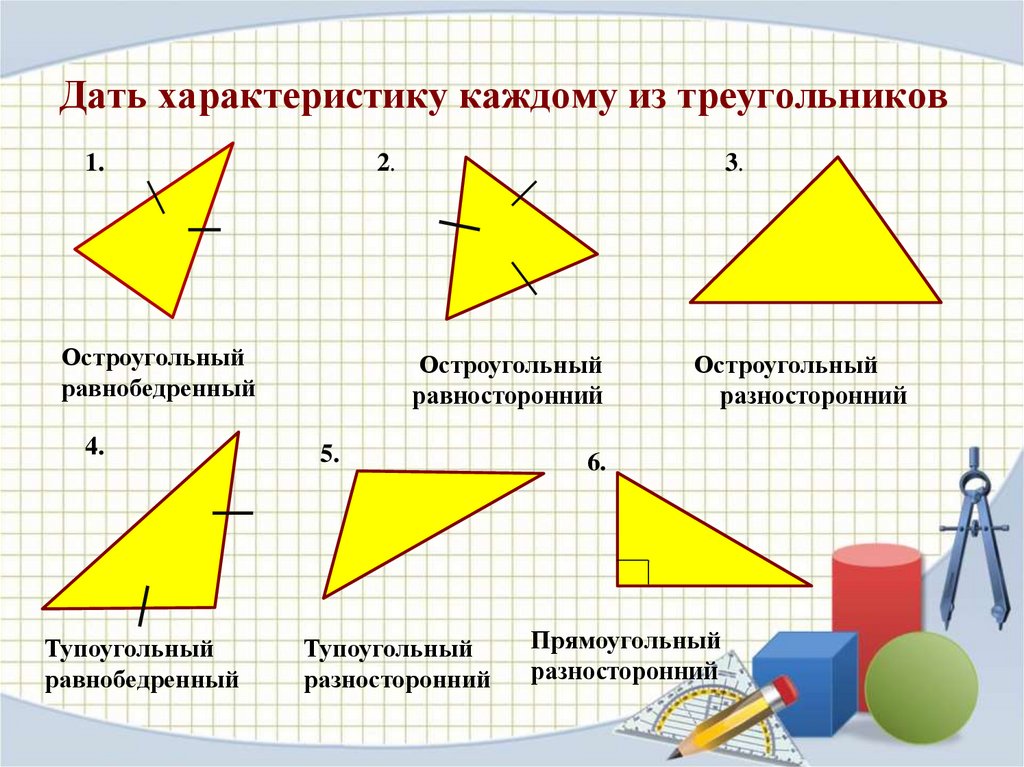
Дать характеристику каждому из треугольников
1.
2.
Остроугольный
равнобедренный
4.
Тупоугольный
равнобедренный
3.
Остроугольный
равносторонний
5.
Тупоугольный
разносторонний
Остроугольный
разносторонний
6.
Прямоугольный
разносторонний

14.

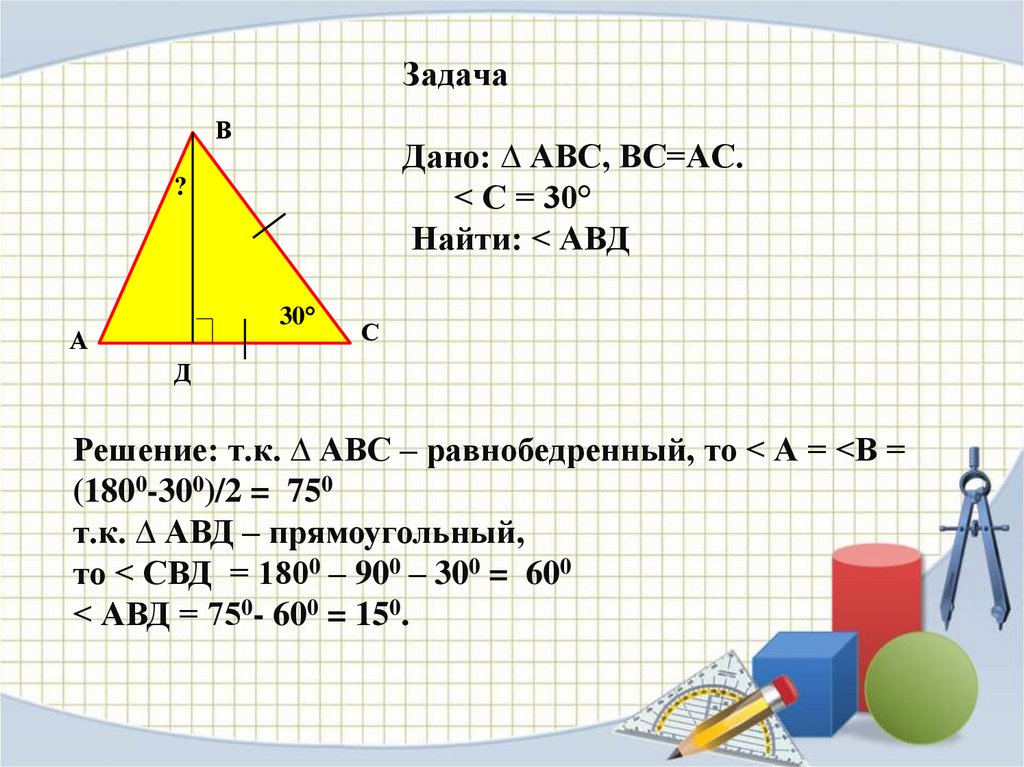
Задача
В
Дано: ∆ АВС, ВС=АС.
< С = 30°
Найти: < АВД
?
30°
А
С
Д
Решение: т.к. ∆ АВС – равнобедренный, то < А = <В =
(1800-300)/2 = 750
т.к. ∆ АВД – прямоугольный,
то < СВД = 1800 – 900 – 300 = 600
< АВД = 750- 600 = 150.

15.

Домашнее задание:
1. п.30, 31. № 323 ( б, г ), № 324.
2. Приготовить кластер: разновидности
треугольника в зависимости от его сторон и
углов.
3. Найти по интернету другие доказательства
теоремы о сумме углов треугольника.
( задания 2 и 3 на выбор учащихся).

16.

Спасибо за урок!