Similar presentations:
Некоторые свойства прямоугольных треугольников. Геометрия. 7 класс
1.
урок на тему:2.
1)повторить определениетреугольника, виды треугольников;
2)рассмотреть свойства
прямоугольных треугольников;
3)научить решать задачи на
применение свойств прямоугольных
треугольников.
3.
1. Продолжить ряд слов:1) острый, прямой, тупой,…
(развёрнутый угол)
2) точка, отрезок, луч, …
( прямая )
3) точка, отрезок, треугольник, …
( четырёхугольник )
4) остроугольный, прямоугольный, …
(тупоугольный
треугольник )
4.
ТреугольникГеометрическая фигура,
состоящая из трёх точек, не
лежащих на одной прямой и
соединённых отрезками,
называется треугольником
5. Треугольники бывают
• Прямоугольные• Остроугольные
• Тупоугольные
• Равносторонние
• Равнобедренные
• Разносторонние
6. Прямоугольные
Если один изуглов
треугольника
прямой, то
треугольник
называется
прямоугольным.
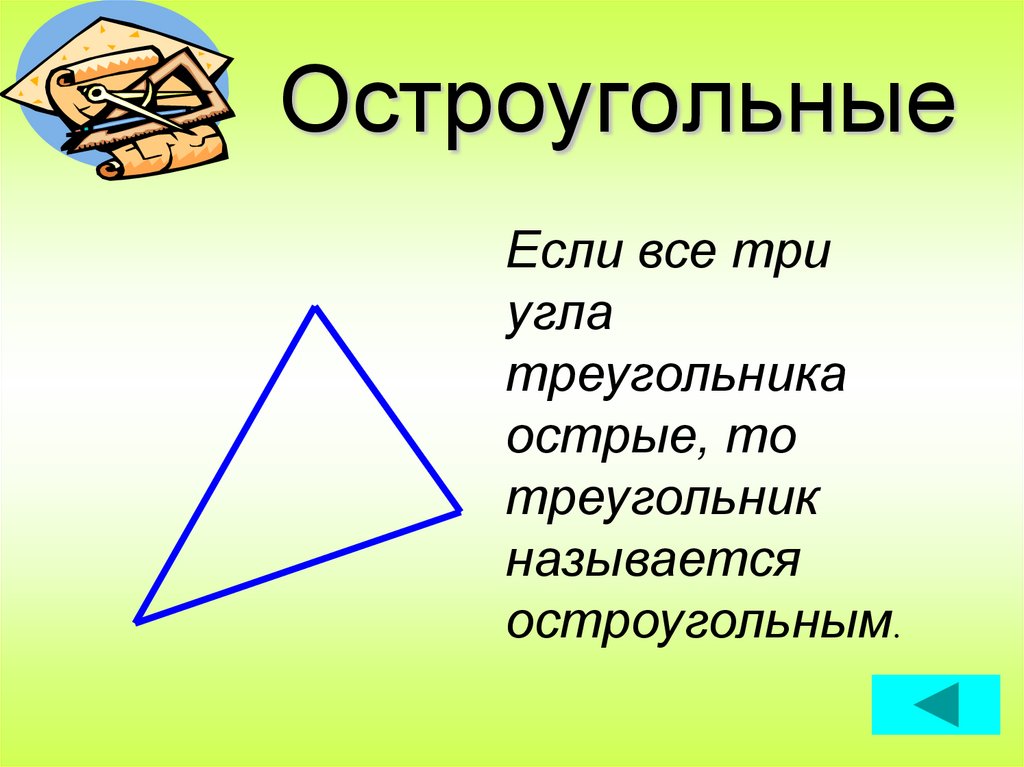
7. Остроугольные
Если все триугла
треугольника
острые, то
треугольник
называется
остроугольным.
8. Тупоугольные
Если один изуглов
треугольника
тупой, то
треугольник
называется
тупоугольным.
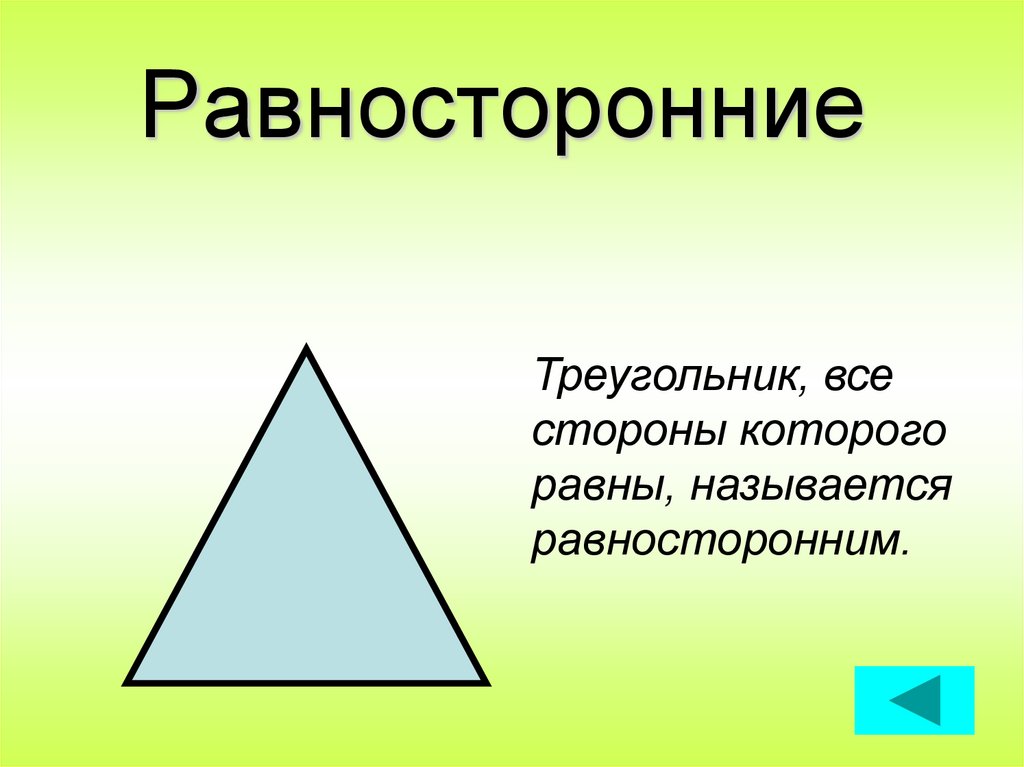
9. Равносторонние
Треугольник, всестороны которого
равны, называется
равносторонним.
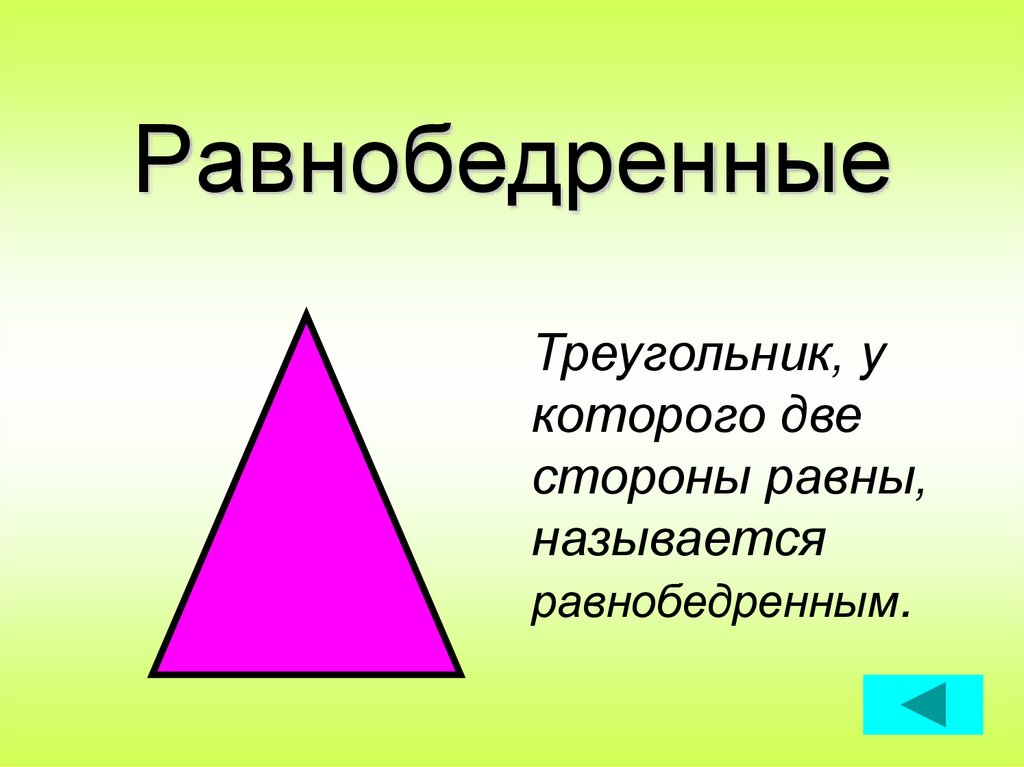
10. Равнобедренные
Треугольник, укоторого две
стороны равны,
называется
равнобедренным.
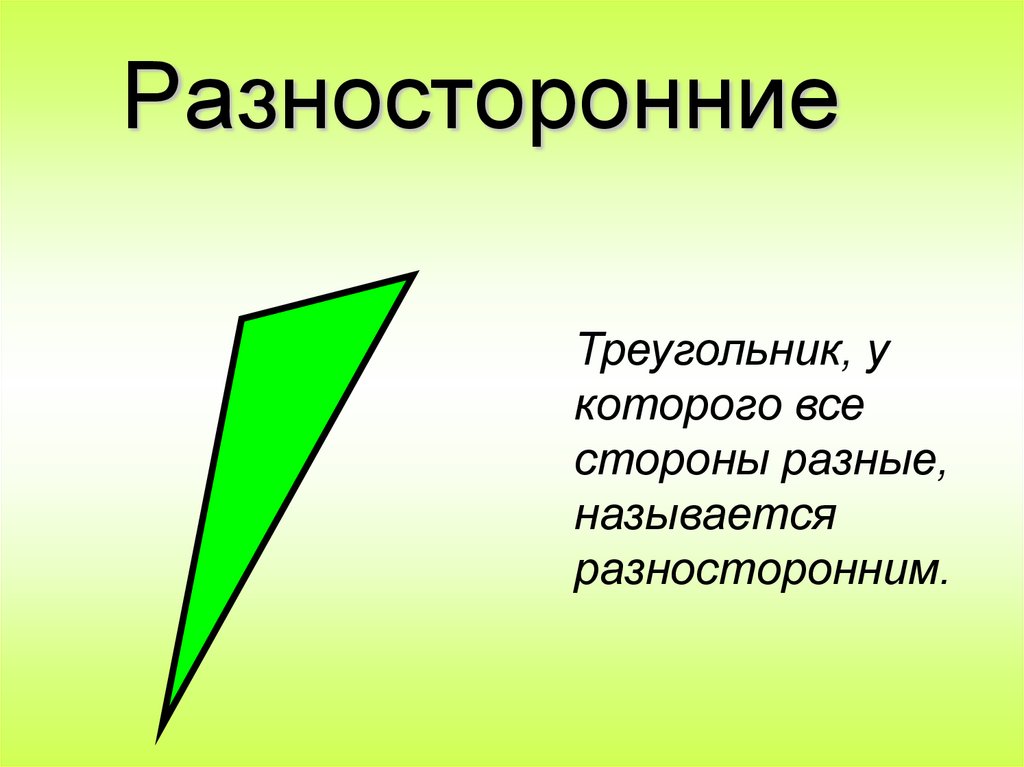
11. Разносторонние
Треугольник, укоторого все
стороны разные,
называется
разносторонним.
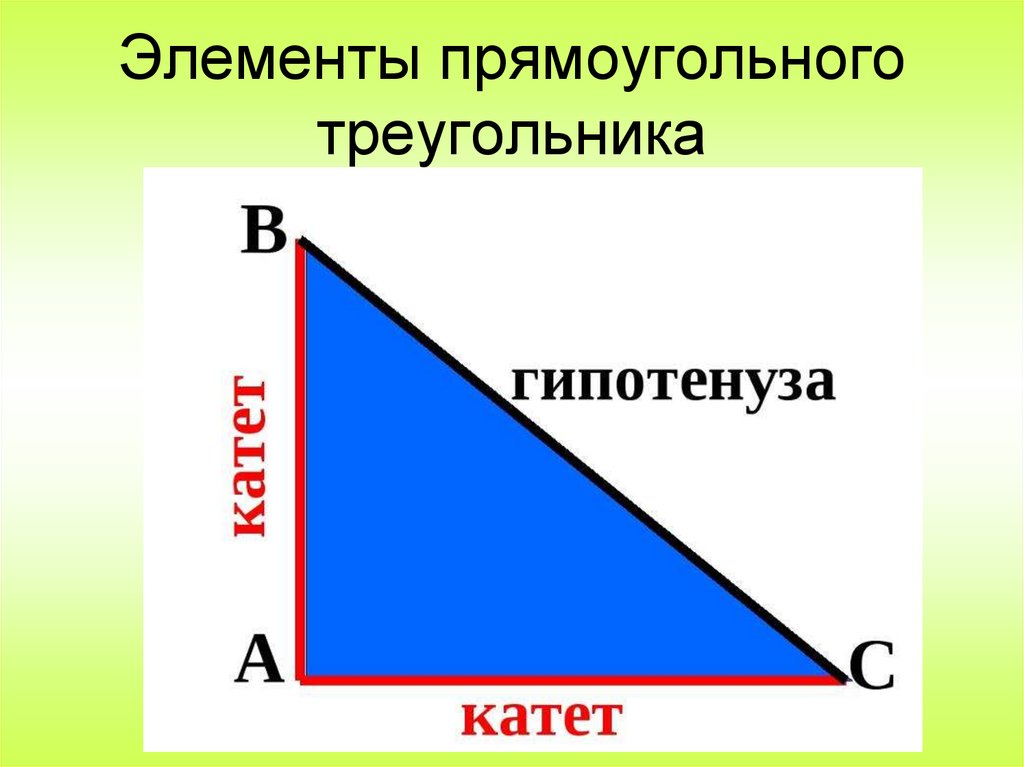
12. Элементы прямоугольного треугольника
13.
Найдите углыравнобедренного
прямоугольного
треугольника
Ответ: 90°,45°, 45°.
14.
Сумма двух острых углов прямоугольноготреугольника равна 90°
Доказательство:
Сумма углов треугольника равна
180° , а прямой угол равен 90° ,
поэтому сумма двух острых углов
прямоугольного треугольника равна
90° .
15.
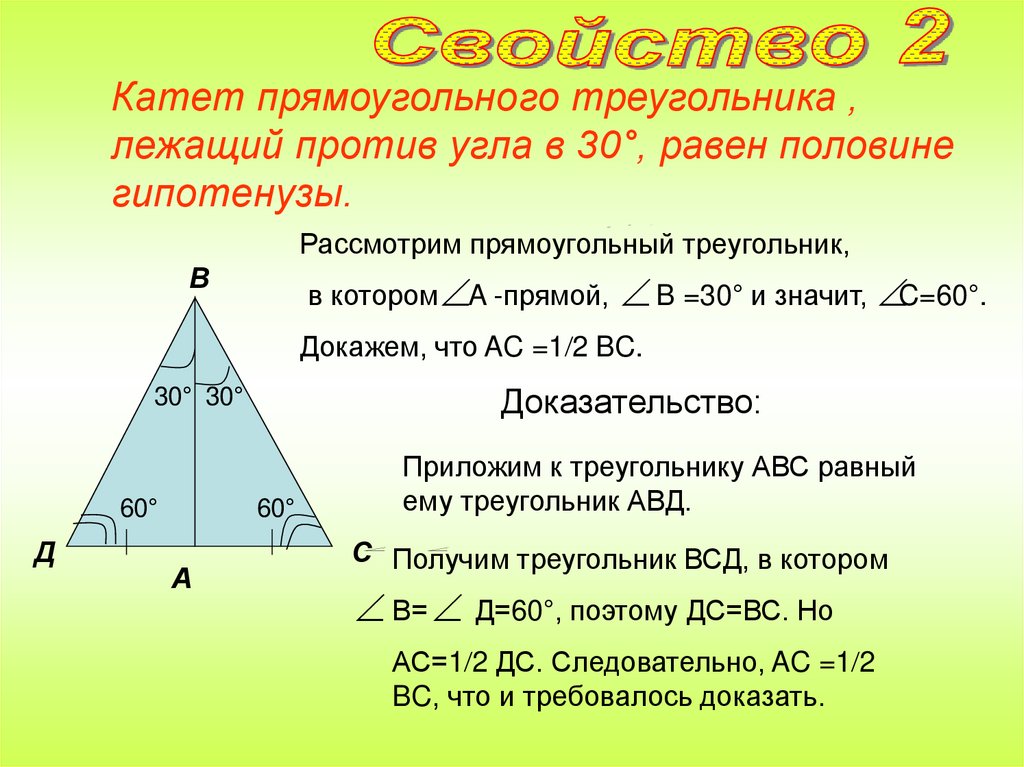
Катет прямоугольного треугольника ,лежащий против угла в 30°, равен половине
гипотенузы.
Рассмотрим прямоугольный треугольник,
В
в котором A -прямой, B =30° и значит, C=60°.
Докажем, что AC =1 2 BC.
Доказательство:
30° 30°
60°
Д
Приложим к треугольнику АВС равный
ему треугольник АВД.
60°
С Получим треугольник ВСД, в котором
А
В= Д=60°, поэтому ДС=ВС. Но
АС=1 2 ДС. Следовательно, AC =1 2
BC, что и требовалось доказать.
16.
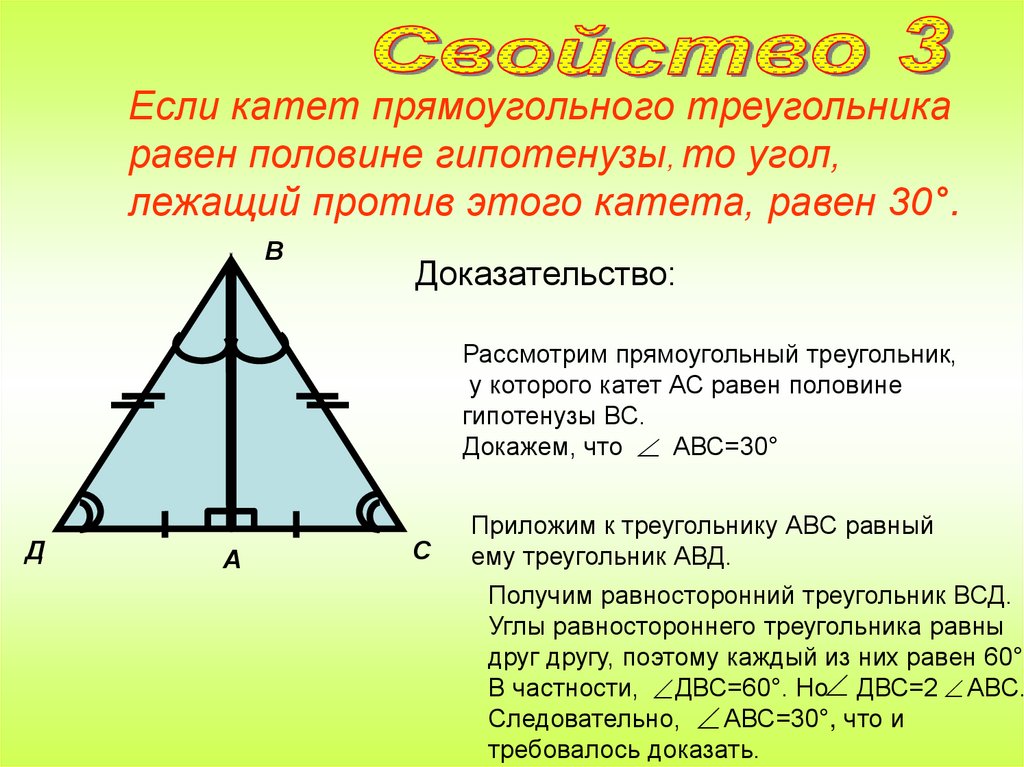
Если катет прямоугольного треугольникаравен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.
В
Доказательство:
Рассмотрим прямоугольный треугольник,
у которого катет АС равен половине
гипотенузы ВС.
Докажем, что АВС=30°
Д
А
С
Приложим к треугольнику АВС равный
ему треугольник АВД.
Получим равносторонний треугольник ВСД.
Углы равностороннего треугольника равны
друг другу, поэтому каждый из них равен 60°.
В частности, ДВС=60°. Но ДВС=2 АВС.
Следовательно, АВС=30°, что и
требовалось доказать.
17.
ВНайти:
угол В
37 0
С
А
18.
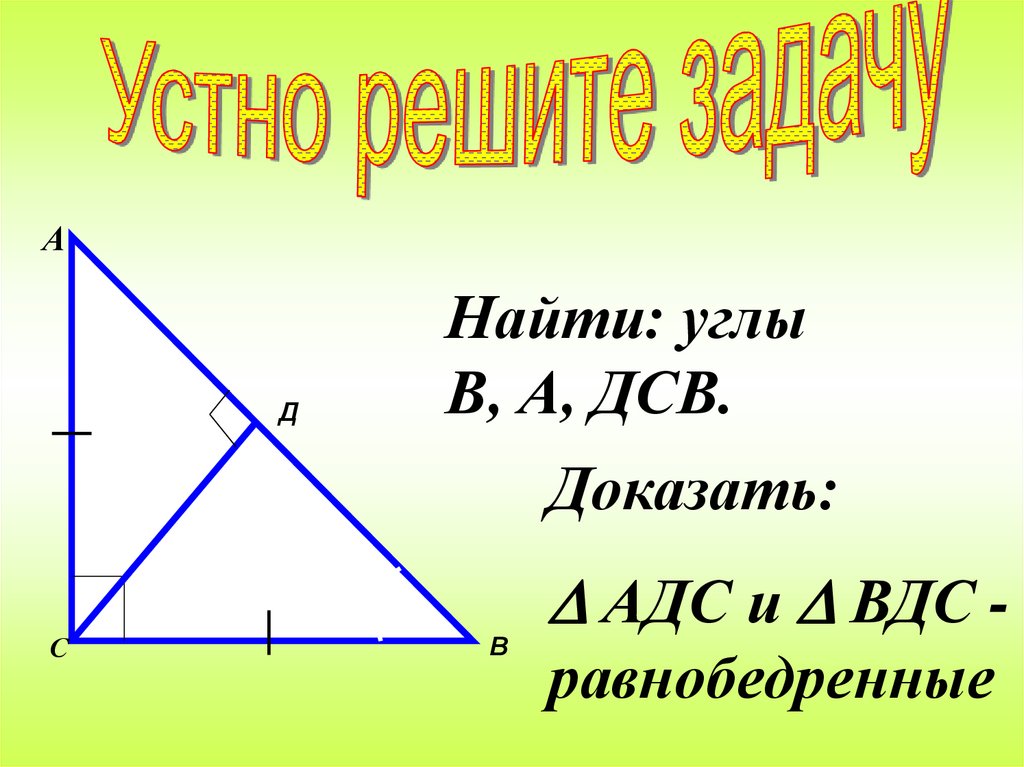
АД
Найти: углы
В, А, ДСВ.
Доказать:
С
В
АДС и ВДС равнобедренные
19.
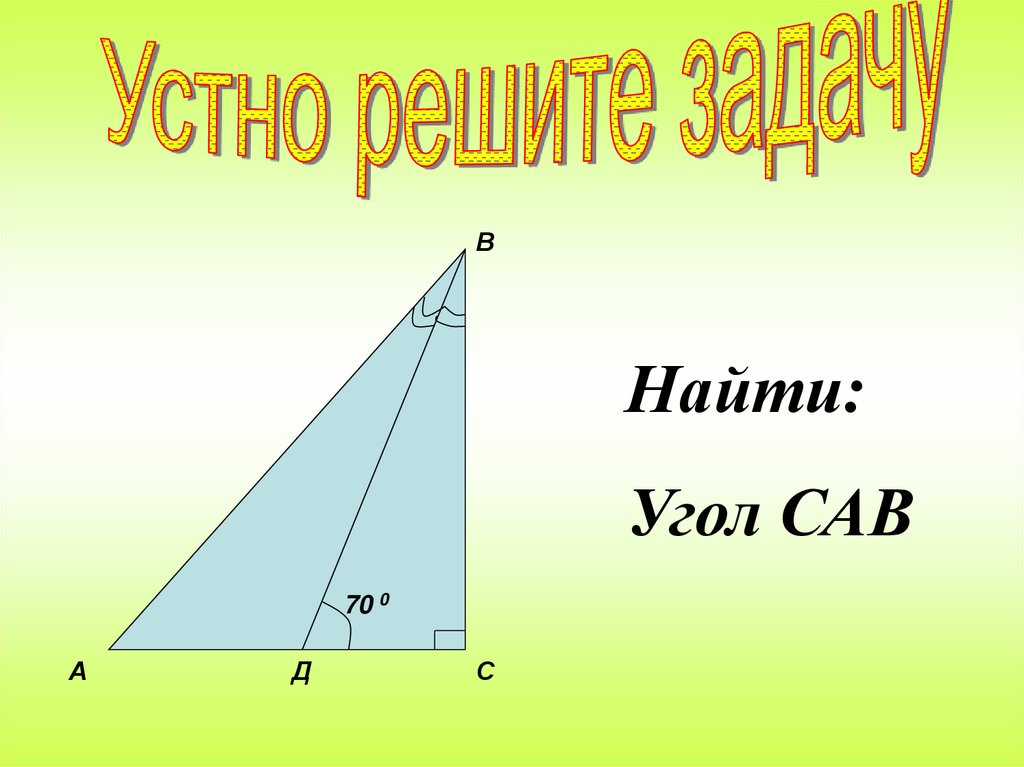
ВНайти:
Угол САВ
70 0
А
Д
С
20.
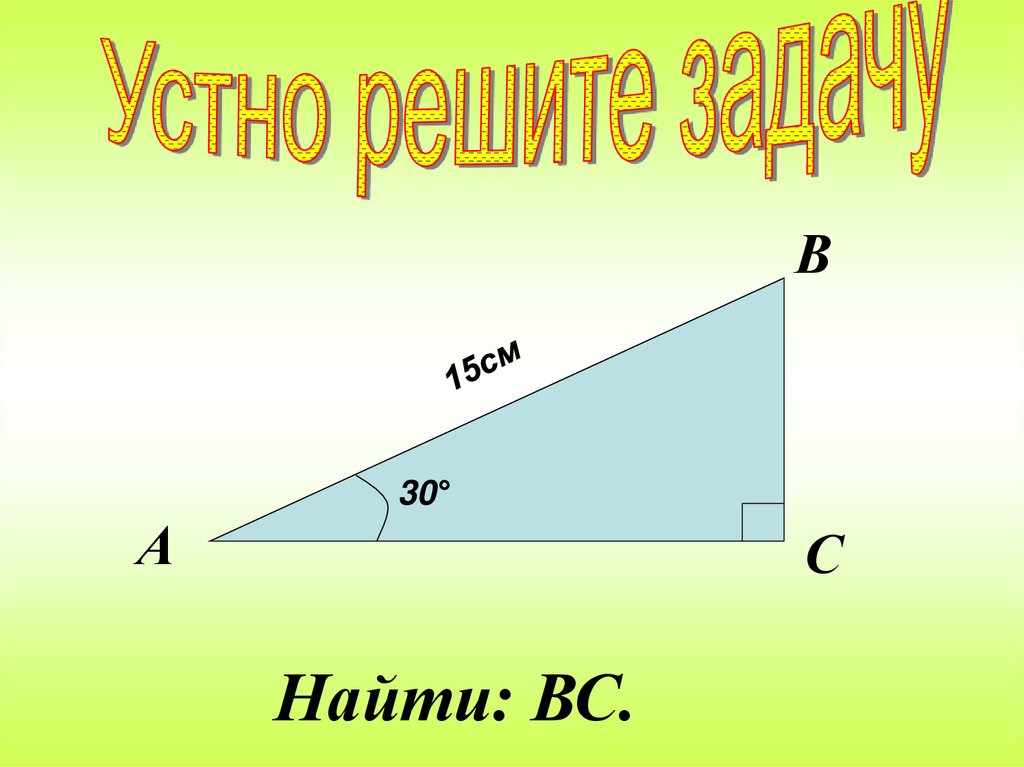
В30°
А
С
Найти: ВС.
21.
Задача (№265)В равнобедренном треугольнике ABC с основанием
AC проведены биссектриса AF и высота AH. Найдите
углы треугольника AHF, если угол B равен 112
A
Дано: АВС – равнобедренный, АС основание, АН – высота, В = 112°.
Найти: углы треугольника AHF.
C
H
B
F
Решение:
1. А С (180 В) / 2 (180 112 ) / 2
68 / 2 34
2. ВАF A / 2 34 / 2 17 , т.к. AF биссектриса
3. AFB 180 - ( B BAF) 180 - 112 17
180 129 51
4. FAH 90 AFH 90 51 39
Ответ: 90°, 39° и 51°.
22.
-Сумма двух острых углов прямоугольноготреугольника равна 90°
-Катет прямоугольного треугольника ,
лежащий против угла в 30°, равен половин
гипотенузы.
-Если катет прямоугольного треугольника
равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.














 mathematics
mathematics








