Применение полного дифференциала в приближенных вычислениях

1.

Применение полного дифференциала
в приближенных вычислениях
u f x x, y y f x, y du
u
u
u
x y .
x
y
u
u
u
u
x y
x
y .
x
y
x
y
Обозначим через u , x , y максимальные абсолютные погрешности (или
границы для абсолютных погрешностей), тогда u
u
u
x
y .
x
y
П р и м е р . Пусть в прямоугольном треугольнике
B
ABC катет AC b и прилежащий угол BAC
измерены, второй же катет a вычисляется по формуле
a a b tg . Как отражаются на значении a погрешности
A
C при измерении b и ?
b
b
da
tg
db
d , то, зная b и ,
Так
как
Рис. 1
cos 2
b
.
можем оценить a по формуле a tg b
2
1
cos

2.

Правила приближенных вычислений
1. Пусть u x y , тогда u x y .
x y
x y
dx
dy dx dy , то
Так как du
x
y
u x y x y .
2. Пусть u xy , тогда u x y .
xy
xy
dx
dy ydx xdy , то
Так как du
x
y
u
u
y x x y x y
x y .
u
xy
x
y
3. Пусть u x / y , тогда u x y .
x / y
x / y
1
x
dx
dy dx 2 dy , то
Так как du
x
y
y
y
u
u x dy x y
x y .
u
x
y
x
y
2

3.

Формула Тейлора
Формула Тейлора с остаточным членом в форме Лагранжа.
Предположим, что f C M . Пусть для заданных x 0 M и направления
n
a
m
выполняется t 0,1 x 0 ta M . Тогда
0,1
1
f x 0 df x 0 ; a d 2 f x 0 ; a
2
1
1
d n 1 f x 0 ; a d n f x 0 a ; a .
n!
n 1 !
Формула Тейлора с остаточным членом в форме Пеано.
Пусть функция f x задана и n 1 раз дифференцируема в некоторой
-окрестности точки x 0 и n раз дифференцируема в самой точке x 0 . Тогда
x B x 0 , справедлива формула:
n
d k f x0; x x0
k 1
k!
f x f x0
.
o n при x , x 0 0
3

4.

Экстремум
Пусть X
m
, f :X
.
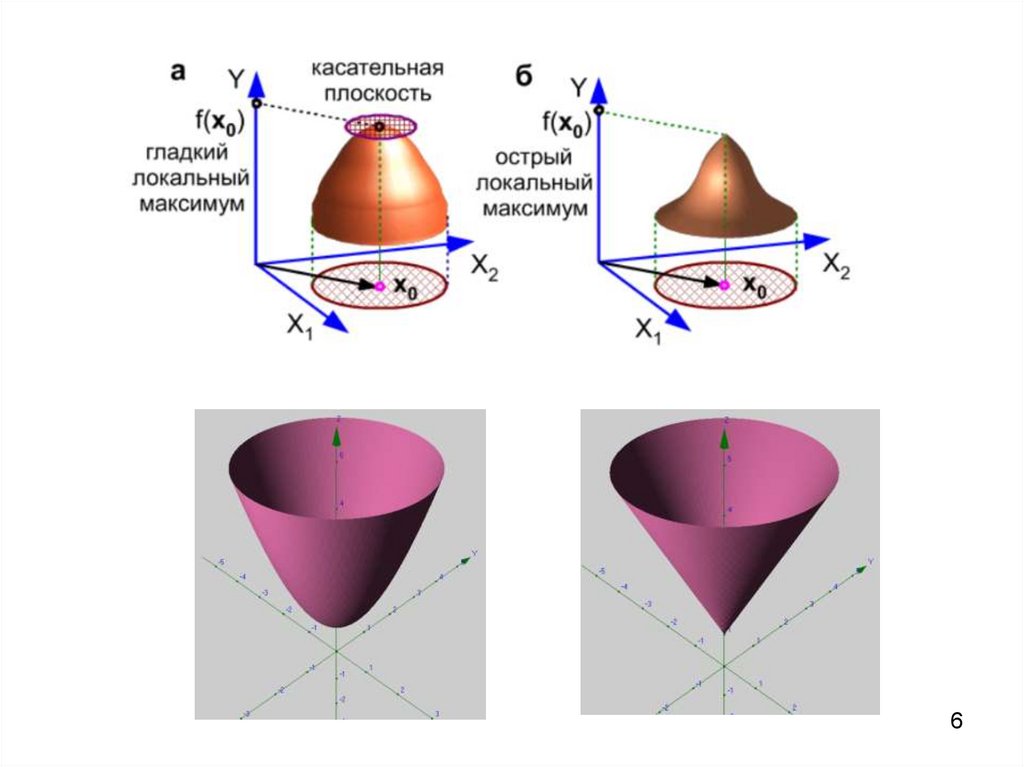
Функция в точке x 0 X имеет абсолютный максимум, если
x X f x f x 0
f x 0 max f x – наибольшее значение функции f на X .
x X
Функция f имеет в точке x 0 локальный максимум, если r 0 :
1) B x , r X ,
0
2) x B x , r
0
f x f x .
0
Локальный максимум называется строгим, если r 0 :
1) B x , r X ,
0
2) x B x , r
0
f x f x .
0
Аналогично определяются понятия абсолютного минимума, наименьшего
значения, локального минимума и строгого локального минимума.
Точки локального максимума и локального минимума называются также
точками локального экстремума.
5

5.

6

6.

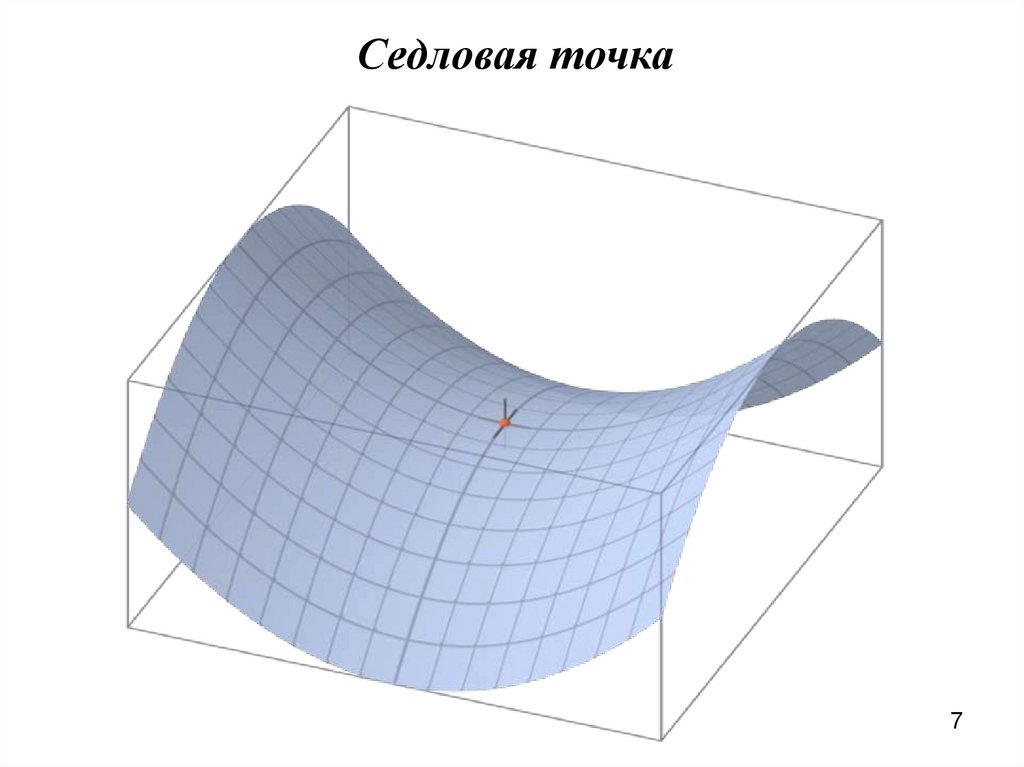
Седловая точка
7

7.

8

8.

Необходимое условие локального экстремума. Если f x : X , X E m
в точке локального экстремума x 0 X имеет все частные производные первого
порядка, то все они равны нулю в точке x 0 .
Следствие. Если f x : X , X E m дифференцируема в точке x 0 и имеет
в этой точке локальный экстремум, то дифференциал df x0 0 .
Внутренние точки области определения функции f x , в которых обращаются
в нуль все частные производные первого порядка, являются точками возможного
экстремума, их называют критическими.
Достаточное условие локального экстремума. Пусть M – открытое множество, x 0 M . Предположим, что f C 2 M и что x 0 есть критическая точка f ,
2 f x0
т.е. f x 0 0 . Тогда если матрица f x 0
xi x j
i , j 1
m
Критерий
Сильвестра
1) положительно определена, то x 0 – точка строгого локального min;
2) отрицательно определена, то x 0 – точка строгого локального max;
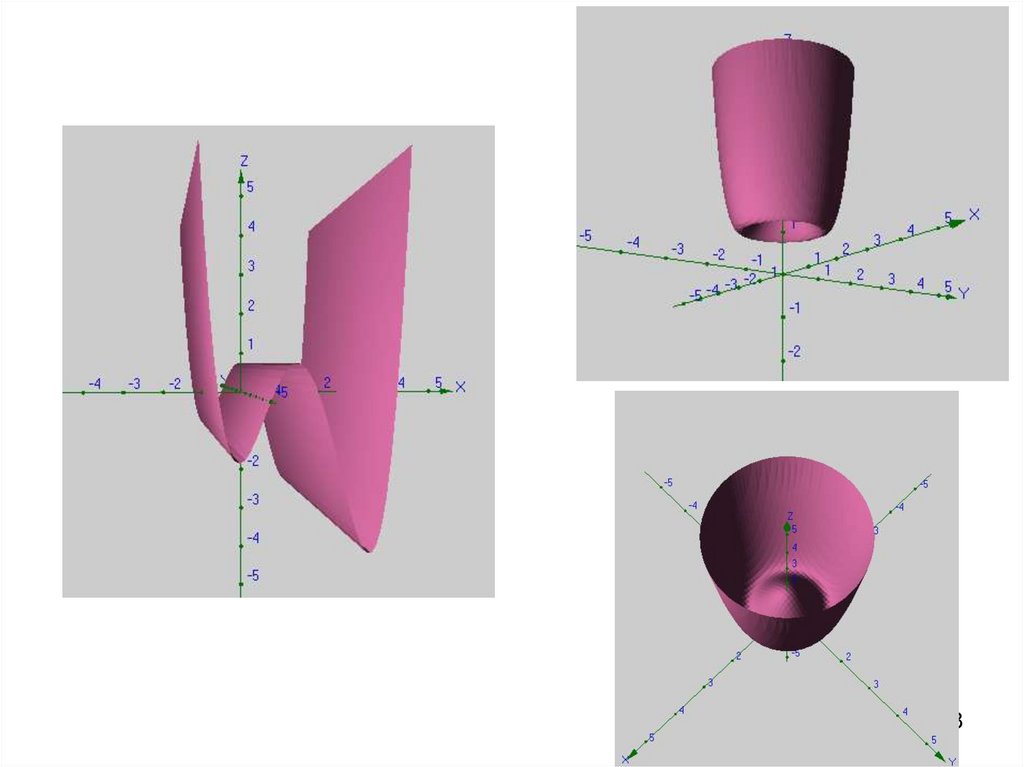
3) является неопределенной, то x 0 не является точкой локального экстремума.
9

9.

Кратчайшее расстояние между скрещивающимися прямыми
x x1 a t1 , x x2 b t2 .
x x a t b t , x x a t b t
x x , x x 2t a, x x 2t b , x x t a, a t b , b 2t t a, b f t , t
2
2 x1 a t1 x2 b t2
1
2
1
2
1
1
1
2
2
2
1
1
2
f
t 2 a , x1 x2 2t1 a , a 2t2 a , b 0
1
f 2 b , x x 2t b , b 2t a , b 0
1
2
2
1
t2
2
2
1
1
2
1
2
2
1 2
a, a
a, b
2
1
2
a , b t a , x1 x2
1
t
b
,
x
x
b,b 2
1
2
t1 , t2 – min, т.к. d 2 f t1 , t2 2dt12 a, a 2dt22 b , b 4dt1dt2 a, b 2 a dt1 b dt2 , a dt1 b dt2 0
a, x x a, b
a, a a, x x a, a a, x x
b, x x
b,b
b , x x b , b
a, b b , x x
a, b b , x x
t
, t
a, a a, b
a, a a, b
a, a a, b
a, a a, b
a, b b , b
a, b b , b
a, b b , b
a, b b , b
a , x1 x2 a , b
1
1
2
1
2
1
2
1
1
2
2
1
2
1
2
2
15

10.

a, b
b , x x b , b
t
,
a, a a, b
a, b b , b
a , x1 x2
f
t 2 a , x1 x2 t1 a , a t2 a , b 0
1
f 2 b , x x t b , b t a , b 0
1
2
2
1
t2
1
a , a a , x1 x2
a, b b , x x
t
a, a a, b
a, b b , b
2
1
1
2
2
2 x1 x2 a t1 b t2 , x1 x2 a t1 b t2
x1 x2 a t1 b t2 , x1 x2 x1 x2 a t1 b t2 , a t1 x1 x2 a t1 b t2 , b t2
x1 x2 , x1 x2 a, x1 x2 t1 b , x1 x2 t2
a, x x a, b
a, a a, x x
a, b
a, x x
b , x x t
x x ,x x
a, b b , x x
a, b b , b
b , x x b , b
a, a a, b
a, b b , b
x x , x x a, x x b , x x
a, x x
a, a
a, b
b, x x
a, b
b,b
a, a a, b
a, b b , b
16
a, a
1
2
1
1
2
1
2
1
1
1
2
2
1
2
1
2
1
2
2
2
1
2
1
2
1
2
1
2
2

11.

Равномерная непрерывность
Функция
f x
называется равномерно непрерывной
на множестве M E m , если
0 0 A , A M A , A f A f A .
Теорема Кантора. Непрерывная на замкнутом ограниченном множестве M функция равномерно непрерывна на нем.
Теорема. Если функция f x , x
m
дифференцируема
в выпуклой области G и все ее частные производные ограничены в G , то f x равномерно непрерывна в G .
17