Решение простейших тригонометрических уравнений. Урок 1

1.

2.

Урок 1
Решение простейших
тригонометрических уравнений
Задание:
1.Переписать слайды 1-7
2.Формулы решения уравнений
выписать в справочный материал.
3.Решить уравнения слайды 6и 8.

3.

Решение уравнения sin x = 1/2
у
1
-π/2
-π
π
0
-1
π/2
2π
3π/2
1
3π
5π/2
х

4.

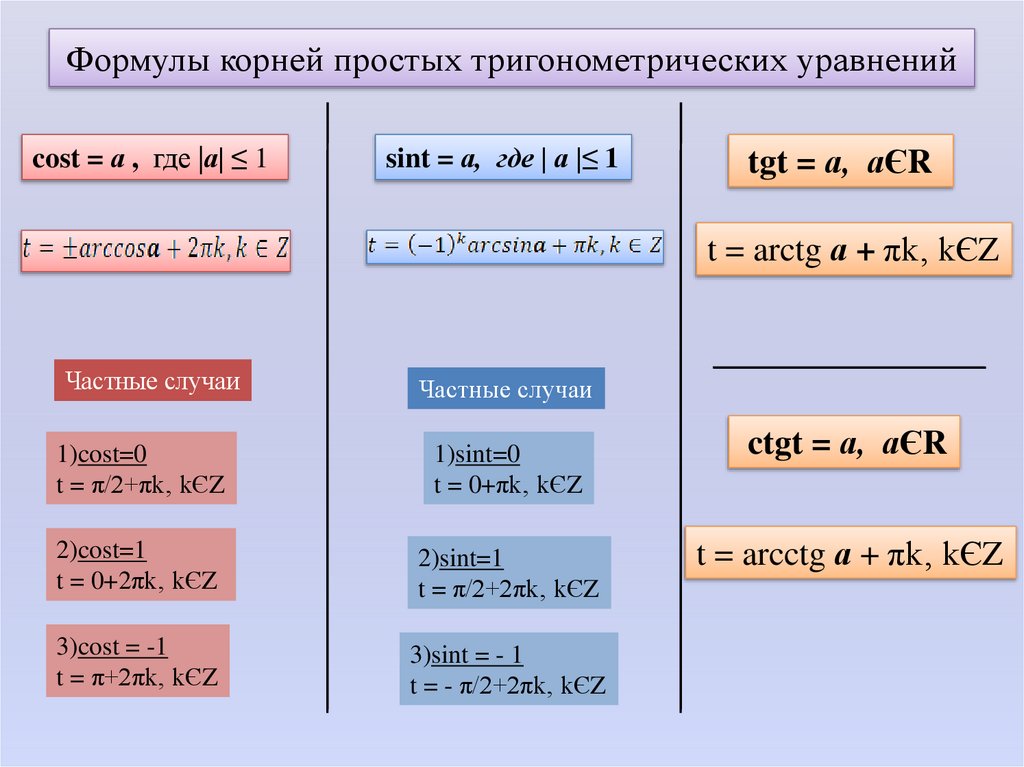
Формулы корней простых тригонометрических уравнений
cost = а , где |а| ≤ 1
sint = а, где | а |≤ 1
tgt = а, аЄR
t = arctg а + πk‚ kЄZ
Частные случаи
Частные случаи
1)cost=0
t = π/2+πk‚ kЄZ
1)sint=0
t = 0+πk‚ kЄZ
2)cost=1
t = 0+2πk‚ kЄZ
2)sint=1
t = π/2+2πk‚ kЄZ
3)cost = -1
t = π+2πk‚ kЄZ
3)sint = - 1
t = - π/2+2πk‚ kЄZ
ctgt = а, аЄR
t = arcctg а + πk‚ kЄZ

5.

Примеры решения уравнений:
1) cost= - ½;
t= ±arccos(-1/2)+2πk, kЄZ
t= ±2π/3+2πk, kЄZ
3) tgt = 1;
t = arctg1+πk, kЄZ
t = π/4+πk, kЄZ.
2) sint = 0;
Частный случай:
t = 0+πk, kЄZ
4) ctgt = t = arcctg( )+πk, kЄZ
t = 5π/6+πk, kЄZ.

6.

Решить уравнения:

7.

Примеры решения простейших уравнений
1) tg2x = -1
2) cos(x+π/3) = ½
2x = arctg (-1) + πk, kЄZ
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/8 + πk/2, kЄZ.
Ответ: -π/3 ± π/3 + 2πk, kЄZ
3) sin(π – x/3) = 0
упростим по формулам
приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.

8.

Решить уравнения

9.

Самостоятельная работа
По теме:
«Решение простейших тригонометрических уравнений»
1 вариант
2 вариант
2 Sin x = - 1
2 Sin 2x = 0
Cos(x – π/3) = - 1
2Cos x = -1
Sin (x – π / 6) = 1/2
Домашнее задание:
- 2 Cos x = 1
2 Sin 3x = - 1
Sin (x – π/3) = 1
Cos 3x = - 1
Cos (x – π / 6) = 1/2

10.

УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ
ТРИГОНОМЕТРИЧЕСКИХ ФОРМУЛ.

11.

МЕТОДЫ РЕШЕНИЯ
ТРИГОНОМЕТРИЧЕСКИХ
УРАВНЕНИЙ:
1. РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ.
2. МЕТОД ПОДСТАНОВКИ.

12.

Метод решения уравнений:
РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ

13.

САМОСТОЯТЕЛЬНАЯ РАБОТА
ВАР.1
№ 626 (1)
№ 628 (1)
№ 635 (1)
Домашнее задание:
ВАР.2
№626 (2)
№628(2)
№635 (2)
ВАР.3
№ 629 (2)
№628 (3)
№ 635 (3)

14.

Виды тригонометрических уравнений
Сводимые к квадратным
a∙sin²x + b∙sinx + c=0
Пусть sinx = p, где |p| ≤1, тогда
a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и
решить простые уравнения.
Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно
не равны нулю, то разделим обе
части уравнения на cosx. Получим:
простое уравнение
a∙tgx + b = 0 или tgx = m
Однородные
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.
Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.

15.

Уравнения, сводимые к
квадратным (решаются методом
подстановки).

16.

Самостоятельная работа
Вариант1
Вариант2
Домашнее задание:

17.

Уравнения однородные
первой степени.

18.

Уравнения однородные
второй степени.

19.

САМОСТОЯТЕЛЬНАЯ РАБОТА
ВАРИАНТ 1
ВАРИАНТ
№624 (1)
№636 (1)
№623 (1)
№628 (1)
№624 (2)
№ 636 (2)
№ 623 (2)
№ 628(2)
2
ВАРИАНТ 3
№ 624(4)
№ 636 (3)
№ 623 (3)
№ 628 (3)

20.

Самостоятельная работа
Вариант1
Вариант2