Similar presentations:
Простейшие тригонометрические уравнения
1.
2.
3.
А.Эйнштейн говорил ,что: «Мне приходится делить время
между политикой и уравнениями.
Однако уравнения, по-моему,
важнее. Политика только для
данного момента, а уравнения будут
существовать вечно».
4.
-1≤а≤1если ΙаΙ>1
решения не имеет
5.
a=1a=0
a= -1
,
6.
7.
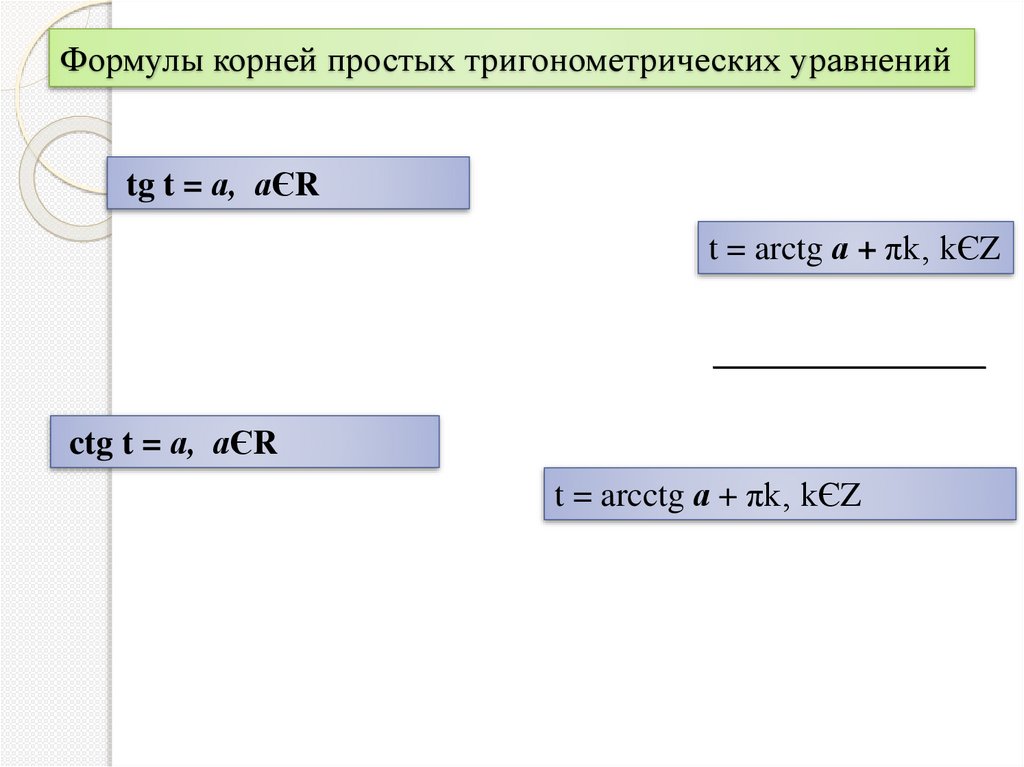
Формулы корней простых тригонометрических уравненийtg t = а, аЄR
t = arctg а + πk‚ kЄZ
ctg t = а, аЄR
t = arcctg а + πk‚ kЄZ
8.
9.
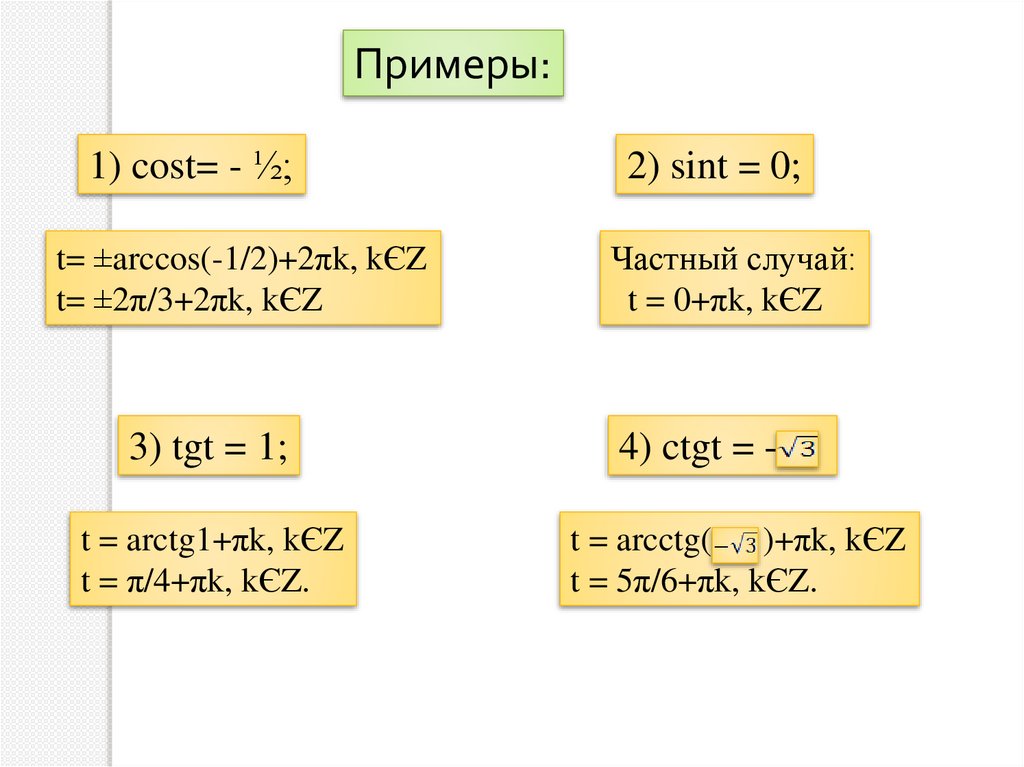
Примеры:1) cost= - ½;
t= ±arccos(-1/2)+2πk, kЄZ
t= ±2π/3+2πk, kЄZ
3) tgt = 1;
t = arctg1+πk, kЄZ
t = π/4+πk, kЄZ.
2) sint = 0;
Частный случай:
t = 0+πk, kЄZ
4) ctgt = t = arcctg( )+πk, kЄZ
t = 5π/6+πk, kЄZ.
10.
Решение простейших уравнений1) tg2x = -1
2) cos(x+π/3) = ½
2x = arctg (-1) + πk, kЄZ
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/8 + πk/2, kЄZ.
Ответ: -π/3 ± π/3 + 2πk, kЄZ
3) sin(π – x/3) = 0
упростим по формулам
приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.
11.
6sin² x + 5cos x - 2 = 0Метод замены
переменной
sin² x – sin 2x = 0
Метод разложения
на множители
cos 6x + cos 2x = 0
Метод преобразования
суммы
в произведение
3 sin² x-4 sinx cosx+cos²x=0
Метод однородных
уравнений
12.
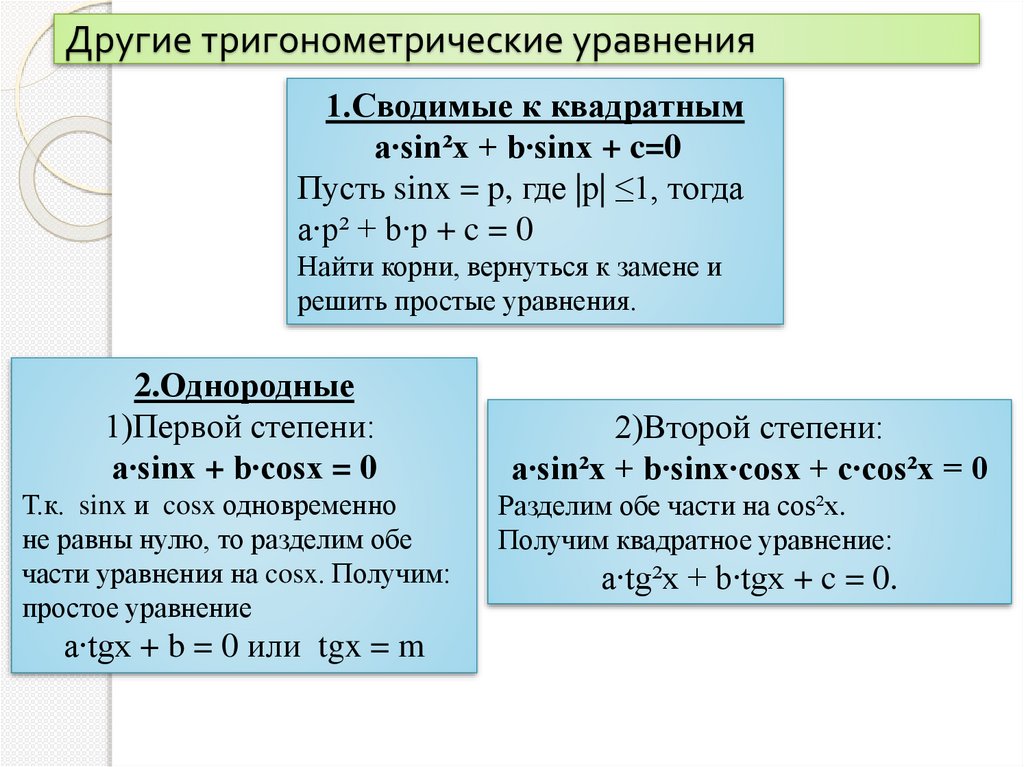
Другие тригонометрические уравнения1.Сводимые к квадратным
a∙sin²x + b∙sinx + c=0
Пусть sinx = p, где |p| ≤1, тогда
a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и
решить простые уравнения.
2.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно
не равны нулю, то разделим обе
части уравнения на cosx. Получим:
простое уравнение
a∙tgx + b = 0 или tgx = m
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.
Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
13.
Однородные уравнения1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно
не равны нулю, то разделим обе
части уравнения на cosx. Получим:
простое уравнение
a∙tgx + b = 0 или tgx = -b\a
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.
Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
14.
3.А sinx + B cosx = C
Решаются с помощью введения вспомогательного аргумента.
При переходе от уравнения (1) к
уравнению (2), могла произойти
потеря корней, значит необходимо
проверить, являются ли корни
уравнения корнями данного
уровнения.
Проверка
Если
,
- не верно, значит
, не является корнями
исходного уравнения
Ответ:
15.
Правила.Увидел квадрат – понижай степень.
Увидел произведение – делай сумму.
Увидел сумму – делай произведение.
16.
I вариантII вариант
Решите уравнения:
1.
1.
2.
2.
3.
3.
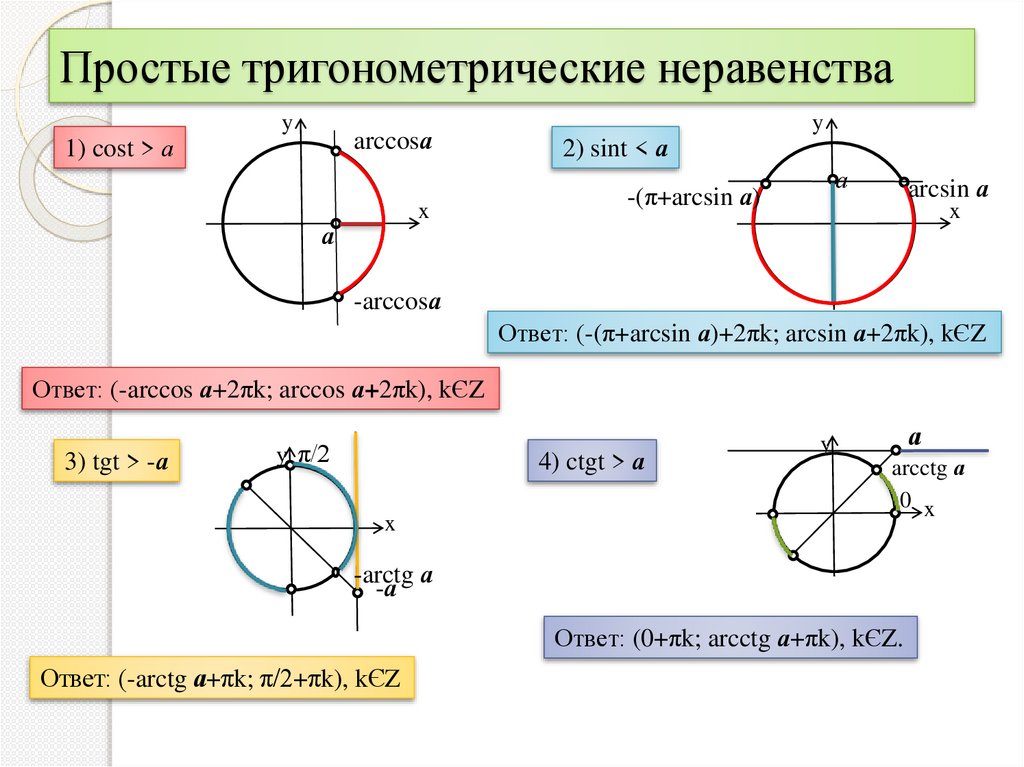
Решите неравенства
4.cos
х













 mathematics
mathematics








