Similar presentations:
Дифференциал булевой функции. Разложение Шеннона (лекция 7.4)
1.
Кафедра Прикладной математикиИнститута информационных технологий
РТУ МИРЭА
Дисциплина
«Математическая логика
и теория алгоритмов»
2023-2024 уч.г.
2.
Лекция 7. Часть 4.Дифференциал булевой функции.
Разложение Шеннона.
3.
Дифференциалом (производной) первого порядка ∂f /∂xi – отБФ f по переменной xi называется логическое выражение:
∂f /∂xi = f(x1,x2,...,xi-1,1,xi+1,...,xn) ⊕ f (x1,x2,...,xi-1,0,xi+1,...,xn),
где f(x1,x2,...,xi-1,1,xi+1,...,xn) – единичная остаточная функция;
f(x1,x2,...,xi-1,0,xi+1,...,xn) – нулевая остаточная функция.
Единичная остаточная функция получается в результате
приравнивания переменной xi к единице,
нулевая – приравнивания xi к нулю.
Замечание 7.2. ! Производная ∂f /∂xi определяет условия, при которых БФ
f изменяет значение при инвертировании переменной xi.
3
4.
Пример 7.6.Найдем производную ∂f /∂x1 БФ (x1,x2,x3) =






















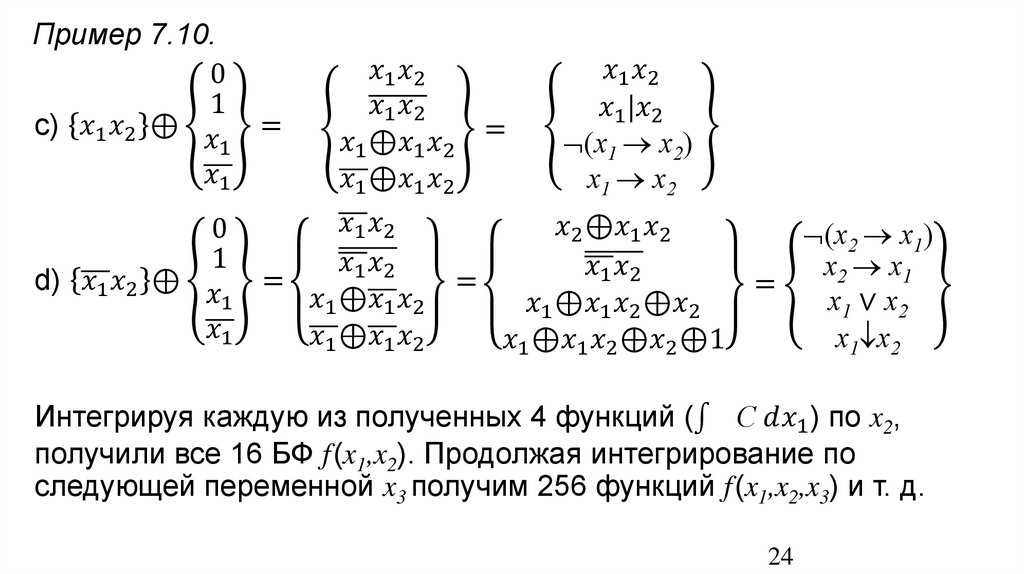









 mathematics
mathematics








