Similar presentations:
Булевы функции и алгебра логики. Двойственность булевых функций
1. Булевы функции и алгебра логики. Двойственность булевых функций
Лекция 72. Тема 1 Булевы функции и алгебра логики
3.
Джордж Буль (1815-1864)Родился в семье рабочего. В 12 лет знал
латынь, затем овладел греческим,
французским, немецким и итальянским
языками. В 16 лет уже преподавал в
деревенской школе, а в 20 открыл
собственную школу в Линкольне.
Начиная с 1839 года Буль стал
посылать свои работы в новый
Кембриджский
математический
журнал. В 1844 году молодой ученый
был награжден медалью Королевского
общества за вклад в математический
анализ.
4.
Вскоре после того как Буль убедился, что егоалгебра вполне применима к логике, в 1847 году он
опубликовал памфлет «Математический анализ
логики», в котором высказал идею, что логика более
близка к математике, чем к философии. Эта работа
была чрезвычайно высоко оценена английским
математиком О. Де Морганом. Благодаря этой работе
Буль в 1849 году получил пост профессора
математики, несмотря на то, что он даже не имел
университетского образования.
В
1854
году
опубликовал
работу
«Исследование законов мышления, базирующихся на
математической логике и теории вероятностей».
4
5.
Работы 1847 и 1854 годов положили начало алгебрелогики, или булевой алгебре. Буль первым показал, что
существует аналогия между алгебраическими и логическими
действиями, так как и те, и другие предполагают лишь два
варианта ответов – истина или ложь, нуль или единица. Он
придумал систему обозначений и правил, пользуясь которыми
можно было закодировать любые высказывания, а затем
манипулировать ими как обычными числами. Булева алгебра
располагала тремя основными операциями – И, ИЛИ, НЕ,
которые позволяли производить сложение, вычитание,
умножение, деление и сравнение символов и чисел. Таким
образом, Булю удалось подробно описать двоичную систему
счисления. В своей работе «Законы мышления» (1854 г.) Буль
окончательно сформулировал основы математической логики.
6.
В 1857 году Буль был избран членомЛондонского Королевского общества. Его работы
«Трактат о дифференциальных уравнениях» (1859 г.)
и «Трактат о вычислении предельных разностей»
(1860 г.) оказали колоссальное влияние на развитие
математики. В них нашли свое отражение наиболее
важные открытия Буля.
Сегодня идеи Буля используются во всех
современных цифровых устройствах.
6
7. Булевы переменные и функции
Переменные, которые могут принимать значениятолько из множества B={0,1}, называются логическими
или булевыми переменными. Сами значения 0 и 1
булевых
переменных
называются
булевыми
константами.
7
8. Булевы переменные и функции
Функция вида y=f(x1,x2,...,xn), аргументы и значениякоторой заданы на множестве B, называется nместной булевой функцией. Такие функции также
называют логическими или переключательными
функциями.
8
9. Основные определения
Кортеж (x1,x2,…,xn) конкретных значений булевыхпеременных называется двоичным словом (n-словом)
или булевым набором длины n.
Для булевой функции y=f(x1,x2,…,xn) конкретное
(индивидуальное) значение булевого набора (x1,x2,…,xn)
называется также интерпретацией булевой функции f.
Множество всех двоичных слов, обозначаемое через
Bn, образует область определения булевой функций и
называется n-мерным булевым кубом и содержит 2n
элементов-слов: |Bn|=2n.
Каждому двоичному слову соответствует одно из
двух возможных значений (0 или 1), таким образом,
область значений представляет собой кортеж длиной 2n,
состоящий из 1 и 0.
9
10. Способы задания булевых функций
I. Таблицы истинностиТаблицы, в которых каждой интерпретации
функции поставлено в соответствие ее значение,
называются таблицами истинности булевой
функции.
В таблице истинности каждой переменной и
значению самой функции соответствует по одному
столбцу, а каждой интерпретации — по одной строке.
Количество строк в таблице соответствует количеству
различных интерпретаций функции.
10
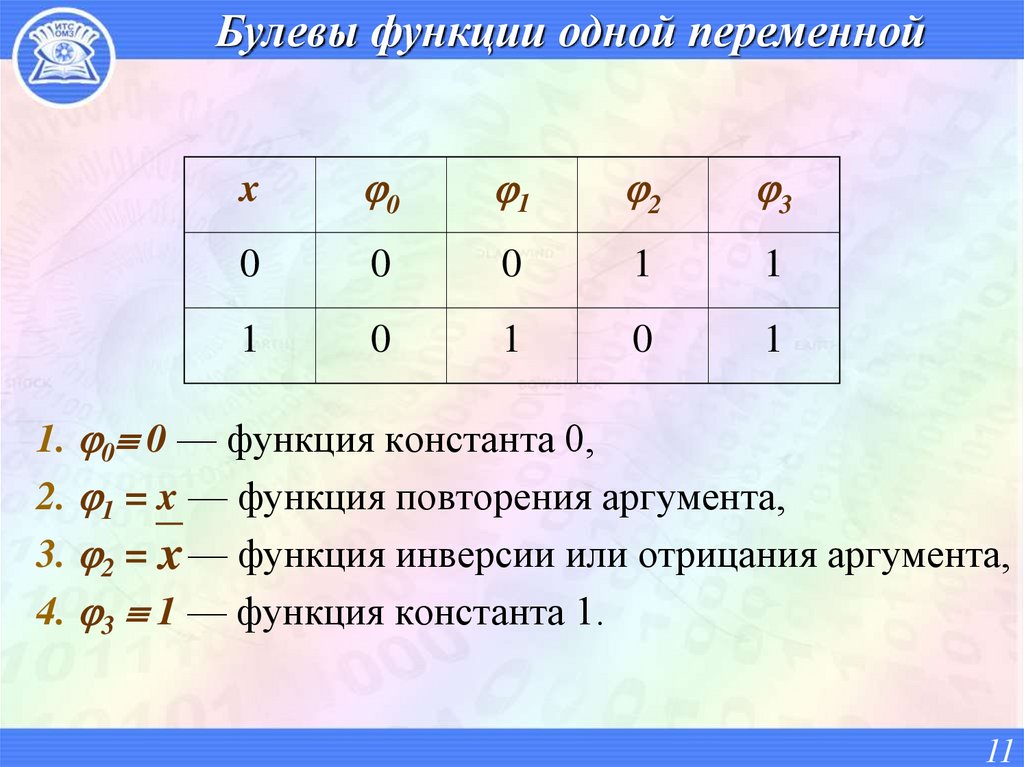
11. Булевы функции одной переменной
x0
1
2
3
0
0
0
1
1
1
0
1
0
1
1. 0 0 — функция константа 0,
2. 1 = x — функция повторения аргумента,
3. 2 = x — функция инверсии или отрицания аргумента,
4. 3 1 — функция константа 1.
11
12. Булевы функции двух переменных
x y f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 f10 f11 f12 f13 f14 f150 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
12
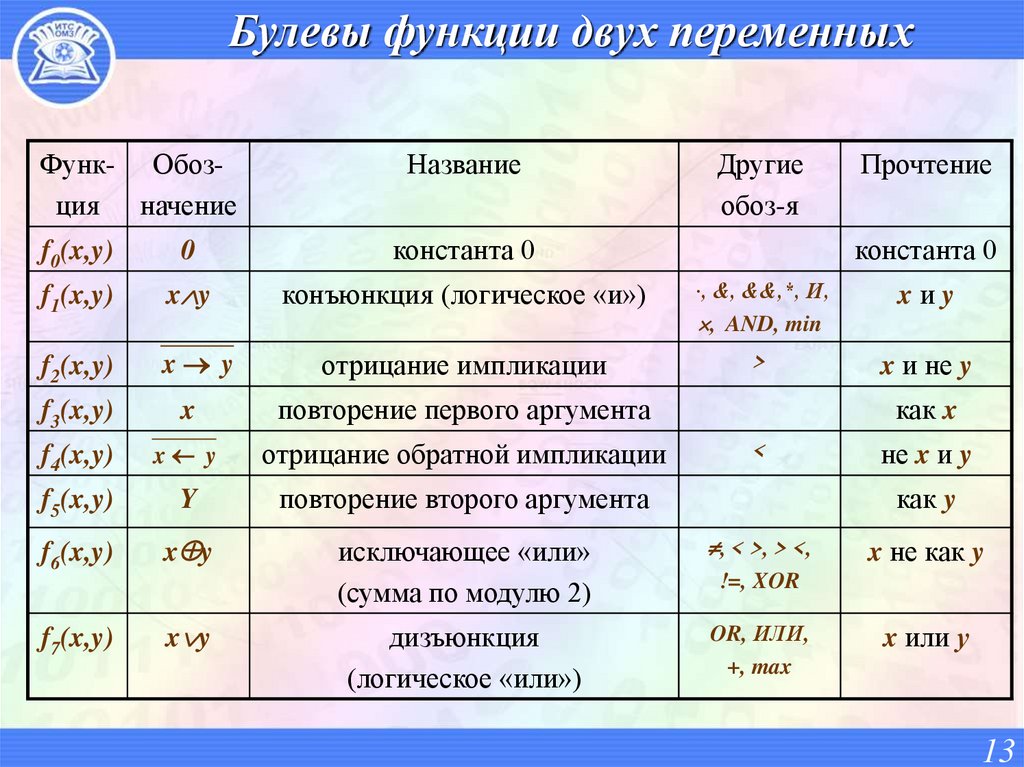
13. Булевы функции двух переменных
Функ- Обозция начениеНазвание
Другие
обоз-я
Прочтение
f0(x,y)
0
константа 0
f1(x,y)
x y
конъюнкция (логическое «и»)
·, &, &&,*, И,
, AND, min
xиy
f2(x,y)
x y
отрицание импликации
>
x и не y
f3(x,y)
x
повторение первого аргумента
f4(x,y)
x y
отрицание обратной импликации
f5(x,y)
Y
повторение второго аргумента
f6(x,y)
x y
исключающее «или»
(сумма по модулю 2)
, < >, > <,
f7(x,y)
x y
дизъюнкция
(логическое «или»)
OR, ИЛИ,
+, max
константа 0
как x
<
не x и y
как y
x не как y
!=, XOR
x или у
13
14. Булевы функции двух переменных
ФункцияОбозначение
Название
Другие
обоз-я
Прочтение
f8(x,y)
x y
отрицание дизъюнкции
(стрелка Пирса)
x y
f9(x,y)
x y
эквивалентность
, , Eqv, =
f10(x,y)
отрицание второго аргумента
y
не y
f11(x,y)
y
x y
обратная импликация
x, если y
(x или не y)
f12(x,y)
x
отрицание первого аргумента
x
не x
если x, то y
(не x или y)
не x и не y
f13(x,y)
x y
импликация
, , Imp
f14(x,y)
x|y
отрицание конъюнкции
(штрих Шеффера)
x y
f15(x,y)
1
константа 1
x как y
не x или не y
константа 1
14
15. Способы задания булевых функций
II. Номера булевых функций и интерпретацийКаждой функции присваивается порядковый номер
в виде натурального числа, двоичный код которого
представляет собой столбец значений функции в
таблице истинности.
Младшим разрядом считается самая нижняя строка
(значение функции на интерпретации (1,1,…,1)), а
старшим — самая верхняя (значение функции на
интерпретации (0,0,…,0)).
15
16. Способы задания булевых функций
Каждойинтерпретации
булевой
функции
присваивается свой номер – значение двоичного кода,
который представляет собой интерпретация.
Интерпретации, записанной в верхней строке
таблицы истинности, присваивается номер 0, затем
следует интерпретация номер 1 и т.д.
В
самой
нижней
строке
расположена
интерпретация с номером 2n–1, где n — количество
переменных, от которых зависит булева функция.
16
17. Пример
Найтипорядковый
номер
функции
f(x,y),
принимающей следующие значения: f(0,0)=1, f(0,1)=1,
f(1,0)=0, f(1,1)=1.
x y f(x,y)
0 0 1
0 1 1
1 0 0
1 1 1
Двоичный код, соответствующий
значению этой функции – 1101.
11012 = 1 23 + 1 22 + 0 21 + 1 20 =
=8+4+0+1=1310
Таким образом
f13(x,y) = (1101)2
17
18. Пример
Построить таблицу истинности для функции f198198 | 2
0 | 99 | 2
1 | 49 | 2
1 | 24 | 2
0 | 12 | 2
0 |6 | 2
0 |3 | 2
1 |1
x
0
0
0
0
1
1
1
1
y
0
0
1
1
0
0
1
1
z f (x,y,z)
0
1
1
1
0
0
1
0
0
0
1
1
0
1
1
0
18
19. Способы задания булевых функций
III. Задание булевых функций с помощью формулФормула – это выражение, задающее некоторую
функцию в виде суперпозиции других функций.
Суперпозицией называется прием получения новых
функций путем подстановки значений одних функций
вместо значений аргументов других функций.
19
20. Пример
Рассмотрим формулу булевой алгебры, задающуюнекоторую функцию f(x,y,z)
f ( x, y,z ) ( x y ) z
Эта формула содержит функции:
g(x1) – отрицание,
s(x1,x2) – конъюнкция,
l(x1,x2) – дизъюнкция.
Представим данную формулу в виде суперпозиции
указанных функций следующим образом:
f (x,y,z) = l(s(x,g(y)),z)
20
21. Приоритет выполнения операций
Если в формуле отсутствуют скобки, тооперации
выполняются
в
следующей
последовательности:
1. Отрицание.
2. Конъюнкция.
3. Дизъюнкция.
4. Импликация.
5. Эквивалентность
Пример
Убрать все возможные скобки
–
~
(( x y ) z ) ( x y ) x y z x y
Расставить скобки с учетом приоритета операций
((
(xx x y y
y))
y (y(yz y ~ z zx~z)
))x~ ~
xy(x
xy
y yy )
21
22. Эквивалентные формулы
Формулы, представляющие одну и ту же функцию,называются эквивалентными или равносильными.
22
23. Законы и тождества алгебры логики
1) Коммутативность конъюнкции и дизъюнкцииx y = y x
x y = y x
2) Ассоциативность конъюнкции и дизъюнкции
x (y z)= (x y) z
x (y z)=(x y) z
3) Дистрибутивность конъюнкции и дизъюнкции
относительно друг друга
x (y z) = (x y) (x z)
x (y z) = (x y) (x z)
23
24. Законы и тождества алгебры логики
4) Идемпотентность конъюнкции и дизъюнкцииx x = x
x x = x
5) Закон исключенного третьего
x x 1
6) Закон противоречия
x x 0
8) Закон элиминации
x (x y) = x
x (x y) = x
24
25. Законы и тождества алгебры логики
7) Тождества с константами.x 0 = x
x 1 = x
x 1 = 1
x 0 = 0
9) Закон двойного отрицания.
x x
10) Законы де Моргана.
x y x y
x y x y
25
26. Тема 2 Двойственность булевых функций
27. Двойственные булевы функции
Функция f*(x1,…,xn) называется двойственной кфункции f(x1,…,xn), если
f ( x 1 ,..., x n ) f ( x 1 ,..., x n )
*
Пример
Найти двойственные функции
( x y )* x y x y
( x y )* x y x y
( x )* x x
(0)* 0 1
(1)* 1 0
27
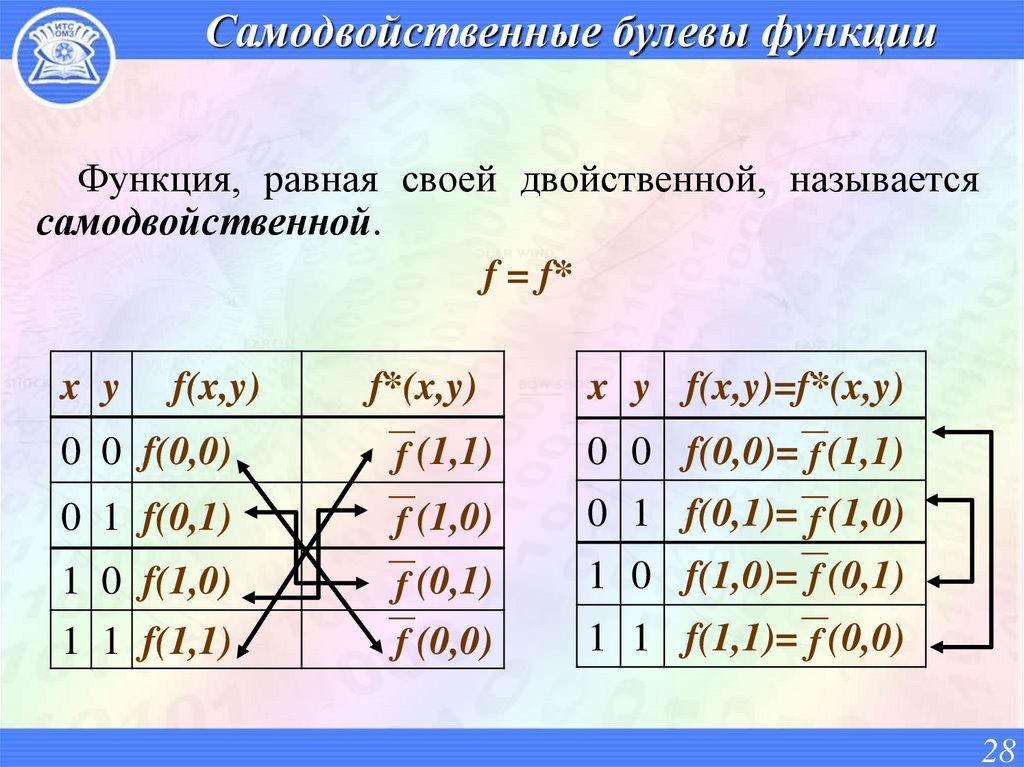
28. Самодвойственные булевы функции
Функция, равная своей двойственной, называетсясамодвойственной.
f = f*
x y
f(x,y)
f*(x,y)
x y f(x,y)=f*(x,y)
0 0 f(0,0)
f (1,1)
0 1 f(0,1)
f (1,0)
0 0 f(0,0)= f (1,1)
0 1 f(0,1)= f (1,0)
1 0 f(1,0)
f (0,1)
1 0 f(1,0)= f (0,1)
1 1 f(1,1)
f (0,0)
1 1 f(1,1)= f (0,0)
28
29.
ПримерЯвляется ли функция f(x,y,z) самодвойственной?
f(x,y,z) —
x y z f (x,y,z) f* (x,y,z)
0 0 0
0
0
0 0 1
1
1
0 1 0
0
1
0 1 1
1
1
1 0 0
0
0
1 0 1
0
1
1 1 0
0
0
1 1 1
1
1
несамодвойственная
29
30. Принцип двойственности
Пусть функция F заданна суперпозициейфункций f0,…,fn, где n N. Функцию F*,
двойственную F, можно получить, заменив в формуле
F функции f0,…,fn на двойственные им f0*,…,fn*.
30
31.
Правило получения двойственных формулДля того чтобы получить двойственную формулу
булевой алгебры необходимо заменить в ней все
конъюнкции на дизъюнкции, дизъюнкции на
конъюнкции, 0 на 1, 1 на 0, и использовать скобки, где
необходимо, чтобы порядок выполнения операций
остался прежним.
31
32.
Правило получения двойственных формулПример
Найти функцию, двойственную функции
f ( x, y,z ) x y y z x z
Решение
f * ( x , y , z ) ( x y y z x z )*
( x y ) ( y z ) ( x z ) ( y x z ) ( x z )
y x y z x z x x z z
x y y z x z x z
x y y z x z f ( x, y,z )
32
33.
Правило получения двойственных формулЕсли функции равны, то и двойственные им функции
также равны.
Пусть f1 и f2 – некоторые функции, заданные
формулами. Тогда если
f1 = f2 ,
то
f1* = f2*
33






























 mathematics
mathematics








