Similar presentations:
Булева алгебра. Основные понятия булевой алгебры
1. БУЛЕВА АЛГЕБРА ОСНОВНЫЕ ПОНЯТИЯ БУЛЕВОЙ АЛГЕБРЫ
ДИСКРЕТНАЯ МАТЕМАТИКАБУЛЕВА АЛГЕБРА
ОСНОВНЫЕ ПОНЯТИЯ БУЛЕВОЙ
АЛГЕБРЫ
ЛЕКЦИЯ 7
С.В.ЧУМАЧЕНКО
Факультет компьютерной инженерии и управления,
кафедра АПВТ, ХНУРЭ
Харьковский национальный университет радиоэлектроники,
кафедра АПВТ, тел. 7021 326, е-mail: ri@kture.kharkov.ua
1
2. Цель лекции – изучить основные положения теории булевых функций для использования точных методов анализа и синтеза при
Основные понятия булевой алгебрыНоябрь, 2003
Тема: Основные понятия булевой алгебры
Цель лекции – изучить основные положения
теории булевых функций для использования
точных методов анализа и синтеза при
проектировании компьютерных систем
Содержание:
• Булевы переменные и функции
• Двоичные наборы
• Основные логические операции
• Таблицы истинности
• Законы булевой алгебры
• ДНФ и КНФ
• СДНФ и СКНФ
• Аналогия с алгеброй множеств Кантора
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
2
3.
Основные понятия булевой алгебрыНоябрь, 2003
Литература
Горбатов В.А. Основы дискретной математики. М.: Высш. шк., 1986. 32-61с.
Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высш. шк.,
1987. 272 с.
Беннеттс Р.Д. Проектирование тестопригодных логических схем: Пер. с
англ. М.: Радио и связь. 1990. 176 с.
Бондаренко М.Ф., Кривуля Г.Ф., Рябцев В.Г., Фрадков С.А., Хаханов В.И.
Проектирование и диагностика компьютерных систем и сетей. К.: НМЦ ВО.
2000. 306 с.
Богомолов А.М., Сперанский Д.В. Аналитические методы в задачах
контроля и анализа дискретных устройств. Саратов: Изд-во Саратовкого
ун-та, 1986. 240с.
Хаханов В.И. Техническая диагностика элементов и узлов персональных
компьюторов. К.: ИСМО, 1997. 308 с.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки
до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ.
2001. 87с.
Новиков Ф.А. Дискретная математика для программистов. С.-П., 2001.
С. 263-268.
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
3
4.
Основные понятия булевой алгебрыНоябрь, 2003
Термины
Базовые понятия:
множество
законы
(ассоциативный,
коммутативный,
элиминации, др.),
бинарные и
унарные операции,
алгебра,
двоичная система
счисления
изоморфизм
структура
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
Ключевые слова:
булева переменная
булева функция
логические операции
(дизъюнкция, конъюнкция,
инверсия, импликация,
сумма по модулю два,
эквивалентность)
дизъюнктивная
нормальная форма (ДНФ)
конъюнктивная
нормальная форма (КНФ)
4
5.
Основные понятия булевой алгебрыНоябрь, 2003
Историческая справка
Родился в Линкольне
1849 – профессор математики Куинс-Колледжа в
Корке (Ирландия)
За работы в области высшего анализа получил
Королевскую медаль
1854 – основное произведение «Исследование
законов мышления»
Предпринял попытку построить формальную логику
в виде некоторого «исчисления», «алгебры»
В современной алгебре встречаются булевы кольца,
булевы алгебры — алгебраические системы, законы
которых берут свое начало от исчисления Буля
В общей топологии – булево пространство
В математических проблемах управляющих систем
− булевы разброс, разложение
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
Джордж Буль
(XIXв.)
5
6. Структура математической логики
Основные понятия булевой алгебрыНоябрь, 2003
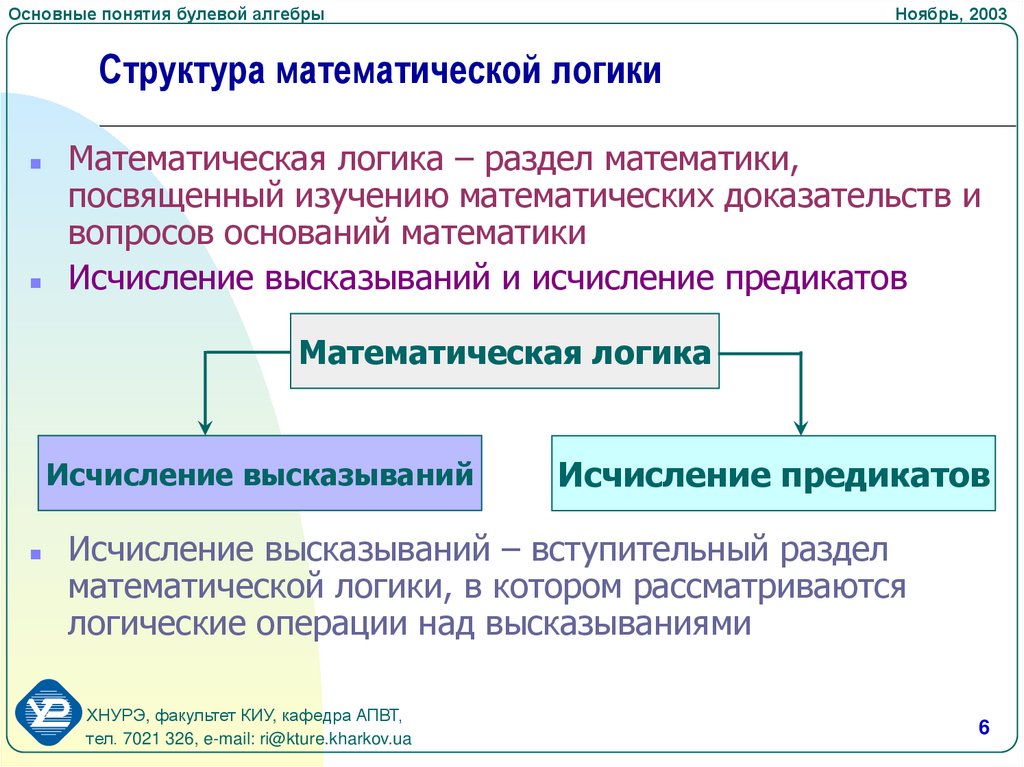
Структура математической логики
Математическая логика – раздел математики,
посвященный изучению математических доказательств и
вопросов оснований математики
Исчисление высказываний и исчисление предикатов
Математическая логика
Исчисление высказываний
Исчисление предикатов
Исчисление высказываний – вступительный раздел
математической логики, в котором рассматриваются
логические операции над высказываниями
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
6
7.
Основные понятия булевой алгебрыНоябрь, 2003
Булевы переменные и булевы функции
В алгебре логики интересуются лишь истинностным
значением высказываний
Обозначения:
1 (истина)
0 (ложь)
Каждой логической операции соответствует функция,
принимающая значения 0, 1, аргументы которой также
принимают значения 0, 1
Def: логическая (булева) переменная
x {0, 1}
Def: логическая (булева) или функция алгебры логики
(ФАЛ)
f(x1, x2, …, xn) {0, 1}
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
7
8.
Основные понятия булевой алгебрыНоябрь, 2003
Двоичные наборы
Переменные булевой функции образуют наборы из
нулей и единиц. Такие наборы называют двоичными
Сколько двоичных наборов имеет функция f(x1, x2, …,xn)
от n переменных?
Булева функция от n переменных определена на 2n
двоичных наборах
Переход от десятичной к двоичной системе счисления:
6
2
–6 3
0 –2
1
2
1
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
(6)10=(110)2
8
9. Двоичные наборы для функций от двух и трех переменных
Основные понятия булевой алгебрыНоябрь, 2003
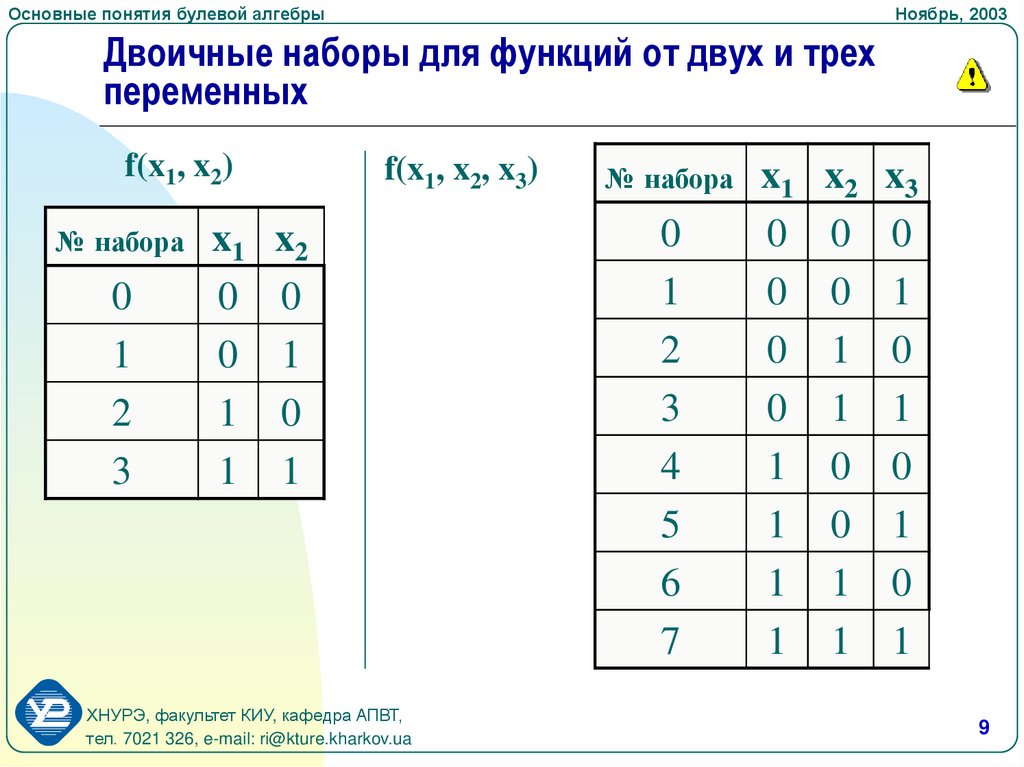
Двоичные наборы для функций от двух и трех
переменных
f(x1, x2)
№ набора
0
1
2
3
x1
0
0
1
1
f(x1, x2, x3)
x2
0
1
0
1
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
№ набора
0
1
2
3
4
5
6
7
x1
0
0
0
0
1
1
1
1
x2
0
0
1
1
0
0
1
1
x3
0
1
0
1
0
1
0
1
9
10. Логические операции
Основные понятия булевой алгебрыНоябрь, 2003
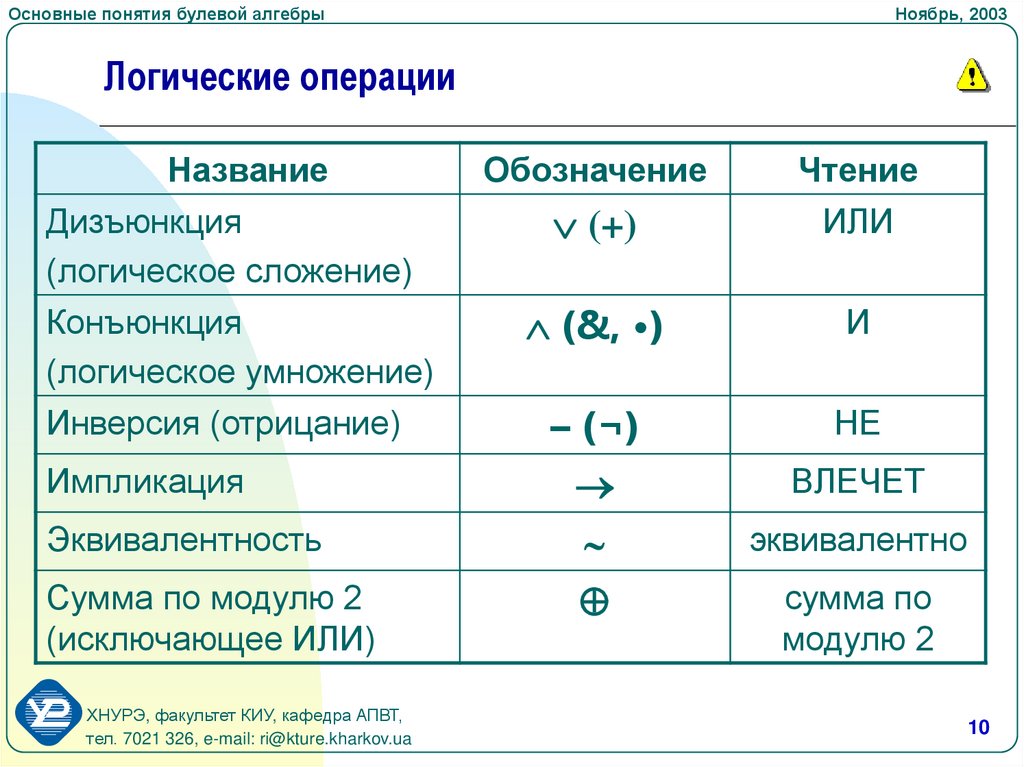
Логические операции
Название
Обозначение
Чтение
Дизъюнкция
(логическое сложение)
Конъюнкция
(логическое умножение)
Инверсия (отрицание)
(+)
ИЛИ
(&, •)
И
– (¬)
НЕ
Импликация
Эквивалентность
Сумма по модулю 2
(исключающее ИЛИ)
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
ВЛЕЧЕТ
эквивалентно
сумма по
модулю 2
10
11. Определение логических операций. Таблицы истинности
Основные понятия булевой алгебрыНоябрь, 2003
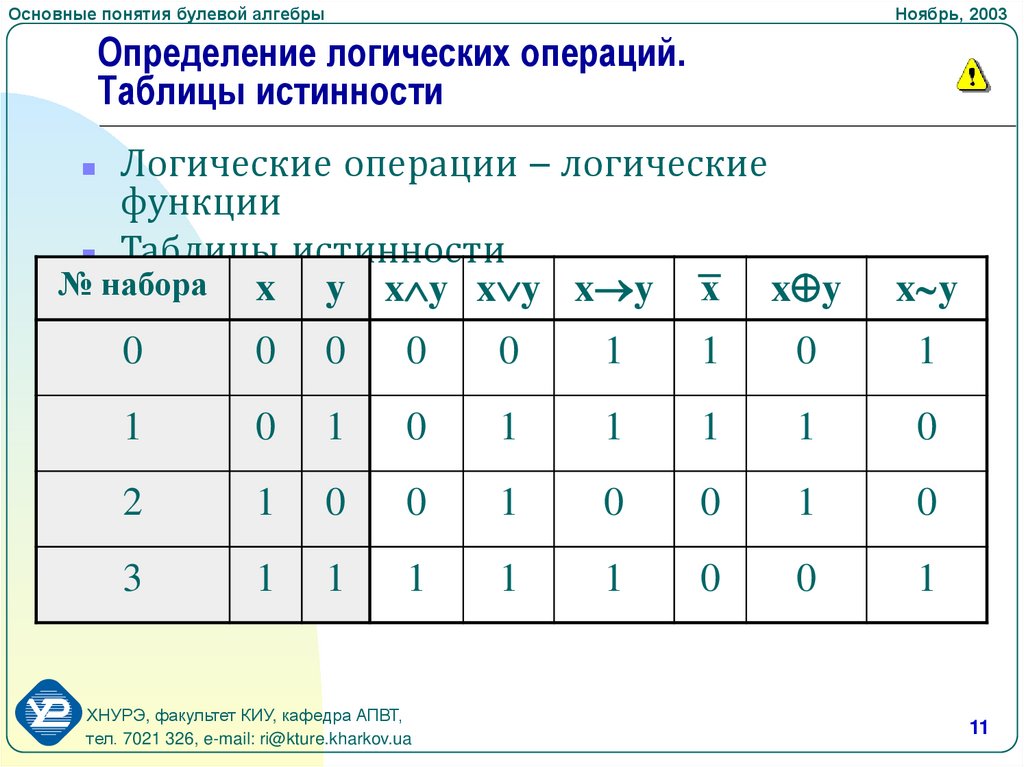
Определение логических операций.
Таблицы истинности
Логические операции – логические
функции
Таблицы истинности
№ набора x y x y x y x y х x y
x y
0
0
0
0
0
1
1
0
1
1
0
1
0
1
1
1
1
0
2
1
0
0
1
0
0
1
0
3
1
1
1
1
1
0
0
1
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
11
12. Пример
Основные понятия булевой алгебрыНоябрь, 2003
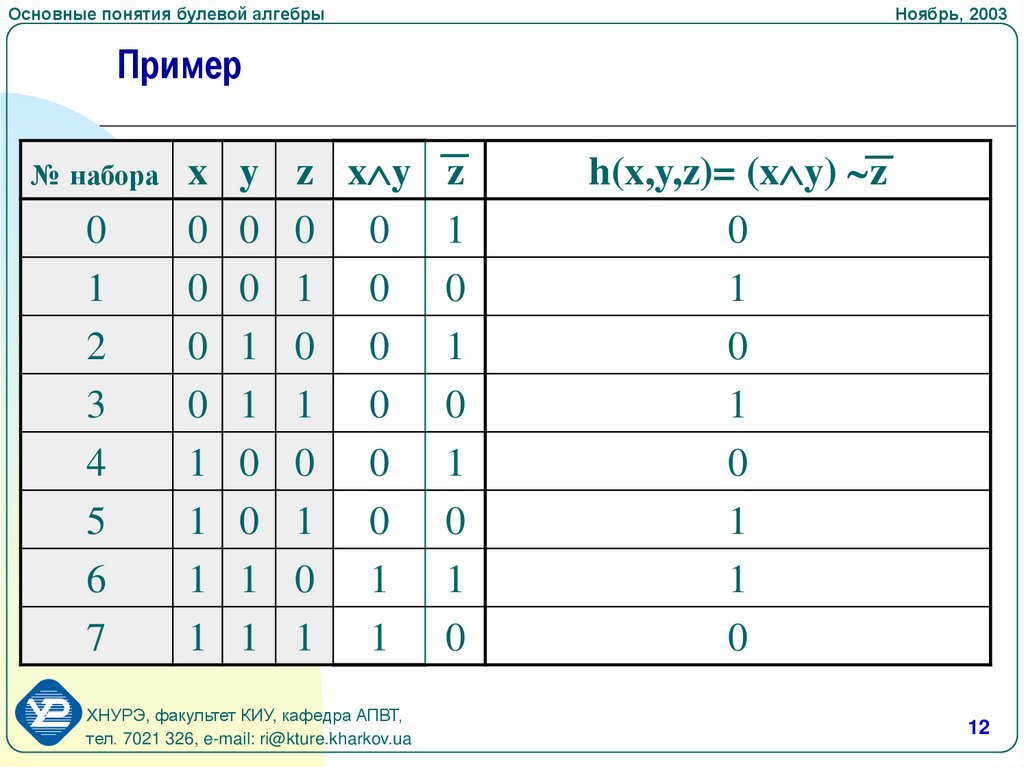
Пример
№ набора
0
1
2
3
4
5
6
7
x
0
0
0
0
1
1
1
1
y
0
0
1
1
0
0
1
1
z x y z
0 0 1
1 0 0
0 0 1
1 0 0
0 0 1
1 0 0
0 1 1
1 1 0
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
h(x,y,z)= (x y) z
0
1
0
1
0
1
1
0
12
13. Time-Out
Основные понятия булевой алгебрыНоябрь, 2003
Time-Out
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
13
14.
Основные понятия булевой алгебрыНоябрь, 2003
Законы и тождества алгебры логики. 1
Название
Коммутативность
Ассоциативность
Формула
x y=y x, xy=yx
(x y) z= x (y z), (xy)z= x(yz)
Дистрибутивность
(x y)z=xz yz,
xy z=(x z)(y z)
Идемпотентность
x x=x, x x=x
Действия с
константами
Инволюция
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
x 0=x, x 0=0, x 1=1, x 1=x,
x x=1, x x=0
x=x
14
15.
Основные понятия булевой алгебрыНоябрь, 2003
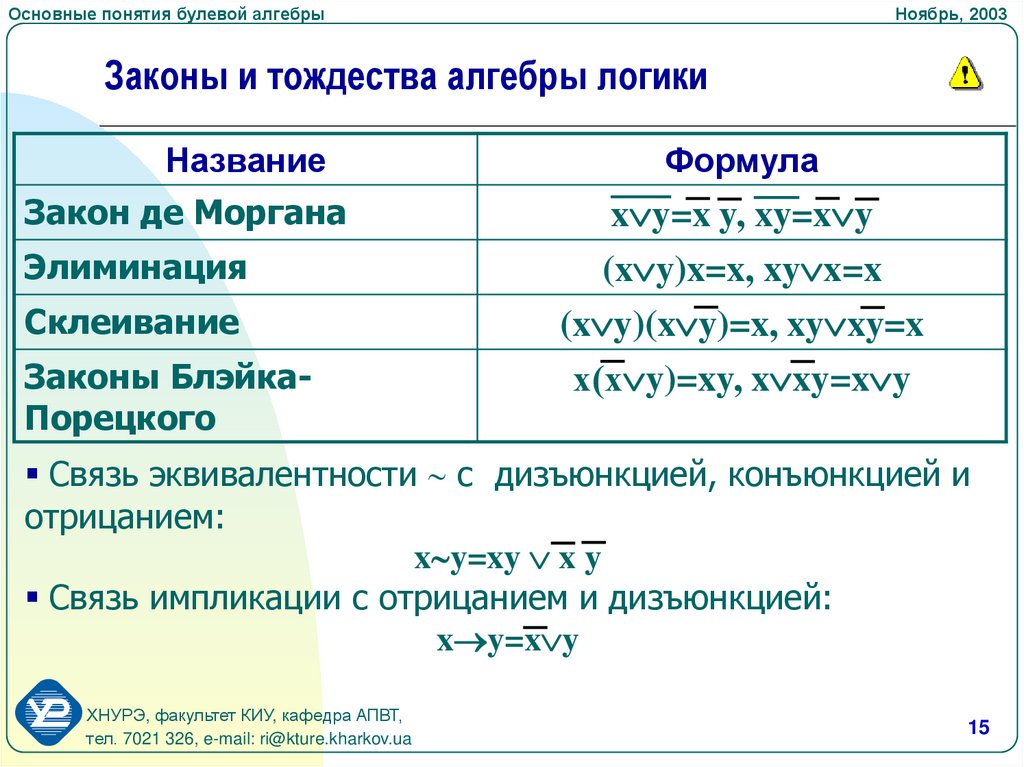
Законы и тождества алгебры логики
Название
Закон де Моргана
Элиминация
Склеивание
Законы БлэйкаПорецкого
Формула
x y=x y, xy=x y
(x y)x=x, xy x=x
(x y)(x y)=x, xy xy=x
х(х y)=xy, x xy=x y
Связь эквивалентности с дизъюнкцией, конъюнкцией и
отрицанием:
x y=xy x y
Связь импликации с отрицанием и дизъюнкцией:
x y=x y
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
15
16.
Основные понятия булевой алгебрыНоябрь, 2003
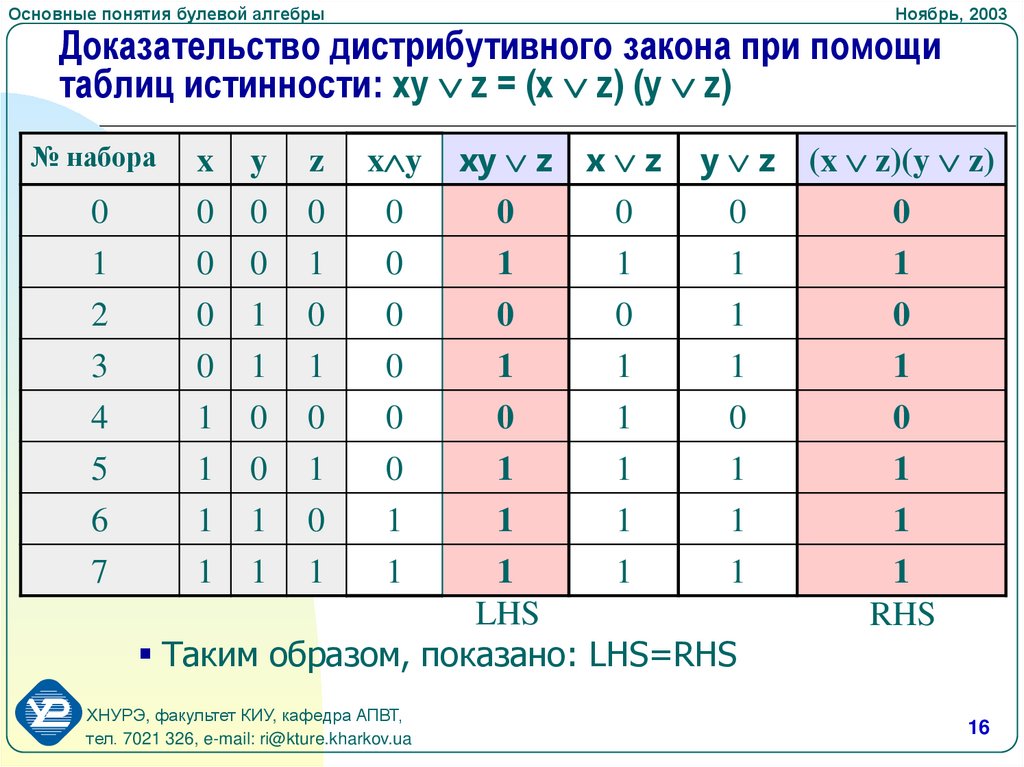
Доказательство дистрибутивного закона при помощи
таблиц истинности: xy z = (x z) (y z)
№ набора
xy z x z
0
0
y z (x z)(y z)
0
0
0
x
0
y
0
z
0
x y
0
1
2
3
0
0
0
0
1
1
1
0
1
0
0
0
1
0
1
1
0
1
1
1
1
1
0
1
4
5
6
1
1
1
0
0
1
0
1
0
0
0
1
0
1
1
1
1
1
0
1
1
0
1
1
7
1
1
1
1
1
1
1
LHS
Таким образом, показано: LHS=RHS
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
1
RHS
16
17.
Основные понятия булевой алгебрыНоябрь, 2003
ДНФ и КНФ
Термин
Обозначение
Первичный терм
x i i
Пример
x i , i 1,
x i , i 0.
x1, x1
( 1 , 2 , ..., n )
Двоичный набор
Элементарная
конъюнкция (ЭК)
ДНФ
x1 1
Элементарная
дизъюнкция (ЭД)
x1 1
& x 2 2
& ... & x n n
(0,1,1,0,1)
n
& x i i
i 1
n
x1x2x3 x1x2
( & x i i )
i 1
x 2 2
КНФ
... x n n
n
&(
i 1
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
i
xi )
x1x2x3x4
n
i 1
x i i
x1 x2 x3 x4
(x1 x2 x3)(x1 x2)
17
18.
Основные понятия булевой алгебрыНоябрь, 2003
Совершенные ДНФ и КНФ (СДНФ и СКНФ). 1
Def: Совершенной ДНФ (СДНФ) называется
ДНФ, в которой нет равных элементарных
конъюнкций и все элементарные конъюнкции
содержат одни и те же переменные, причем
каждую – только один раз (включая вхождения
под знаком отрицания).
Def: Совершенная КНФ (СКНФ)
определяется как такая КНФ, в которой нет
одинаковых сомножителей; все сомножители
содержат одни и те же переменные, причем
каждую переменную – только один раз.
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
18
19.
Основные понятия булевой алгебрыНоябрь, 2003
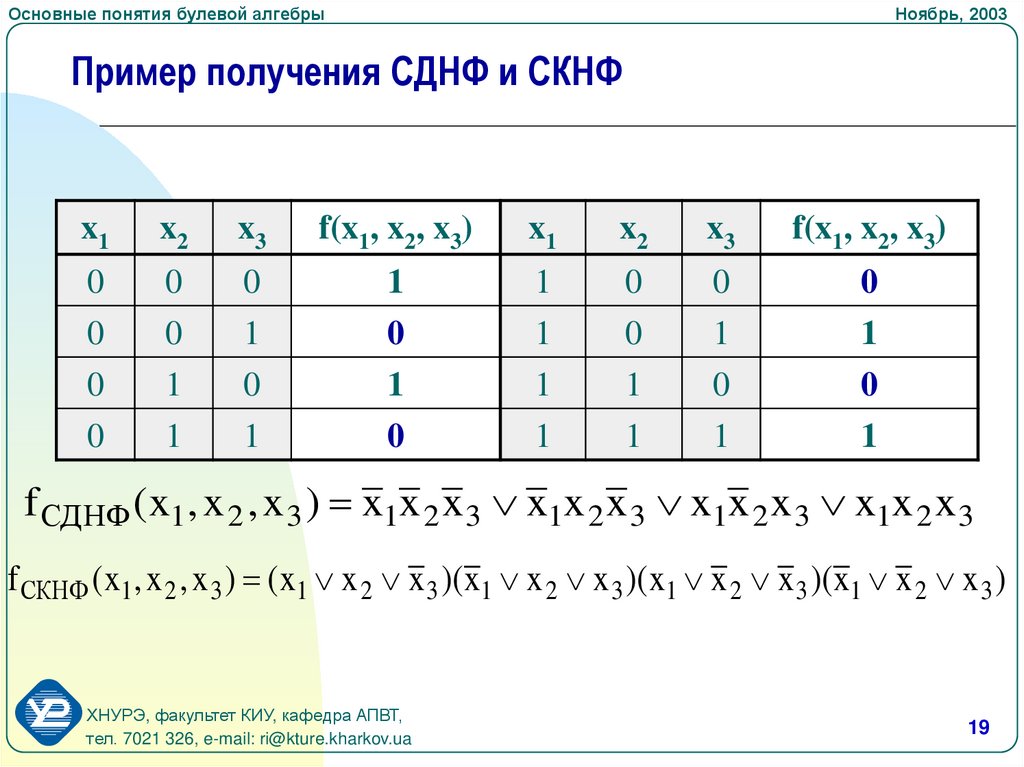
Пример получения СДНФ и СКНФ
x1
x2
x3
f(x1, x2, x3)
x1
x2
x3
f(x1, x2, x3)
0
0
0
0
0
1
1
0
1
1
0
0
0
1
0
1
0
1
0
1
1
1
0
0
0
1
1
0
1
1
1
1
f СДНФ (x1 , x 2 , x 3 ) x1x 2 x 3 x1x 2 x 3 x1x 2 x 3 x1x 2 x 3
f СКНФ ( x1 , x 2 , x 3 ) ( x1 x 2 x 3 )(x1 x 2 x 3 )(x1 x 2 x 3 )(x1 x 2 x 3 )
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
19
20. Теорема Шеннона
Основные понятия булевой алгебрыНоябрь, 2003
Теорема Шеннона
Любая булева функция f 0 представима в виде
разложения Шеннона:
f ( x1 , x 2 ,..., x k , x k 1 , ..., x n )
k
( & x i i ) f ( 1 , 2 ,..., k , x k 1 , ..., x n )
( 1 , 2 ,..., k ) i 1
Следствие
Предельное разложение Шеннона (k=n) булевой
функции f 0 имеет вид
k
i
f ( x1 , x 2 ,..., x k , x k 1 , ..., x n )
(& xi )
( 1 , 2 ,..., n ), i 1
f ( 1 , 2 ,..., n ) 1
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
20
21. Выводы
Основные понятия булевой алгебрыНоябрь, 2003
Выводы
Всякая ФАЛ может быть реализована формулой,
оперирующей символами , , ¬, скобками и
знаком равенства
Любая булева функция может быть представлена в
виде ДНФ, КНФ, СДНФ, СКНФ
ДНФ
КНФ
СДНФ
СКНФ
ДНФ и КНФ есть сокращенная форма записи СДНФ
и СКНФ (таблицы истинности)
ДНФ есть наиболее распространенная форма
описания цифровых систем, максимально
приближенная к аппаратурной реализации
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
21
22. Тест-задание
Основные понятия булевой алгебрыНоябрь, 2003
Тест-задание
Заполнить таблицу истинности для пяти функций:
№ набора
x
y
z
x y
(x y)z
x z
y z
xz yz
0
1
2
3
4
5
6
7
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
22
23. Аналогия с алгеброй множеств Кантора
Основные понятия булевой алгебрыНоябрь, 2003
Аналогия с алгеброй множеств Кантора
Теория множеств
Множество
элементов М
Операция
пересечение
Операция И
( – конъюнкция)
Операция
объединение
Операция ИЛИ
( – дизъюнкция)
Операция
дополнение –
Пустое
множество
Универсум –
множество всех
элементов U
Операция
инверсия –
0-элемент
ХНУРЭ, факультет КИУ, кафедра АПВТ,
тел. 7021 326, e-mail: ri@kture.kharkov.ua
Булева алгебра
Элемент X {0,1}
1-элемент
23















 mathematics
mathematics








