Булевы функции. Лекция 1

1.

ЛЕКЦИЯ 1. БУЛЕВЫ
ФУНКЦИИ

2.

■ Булевой функцией y=f(x1, x2 ... xn) от п переменных x1, x2,
xn называется любая функция, в которой аргументы и функция
могут принимать значение либо 0 либо 1, т.е. булева функция это
правило по которому произвольному набору нулей и единиц (x1,
x2 ... xn) ставится в соответствие значение 0 или 1.
■ Для булевой функции от n аргументов существует 2n различных
наборов аргументов. Поскольку каждая булева функция имеет
конечное количество наборов аргументов, то булеву функцию
можно задать в виде таблицы

3.

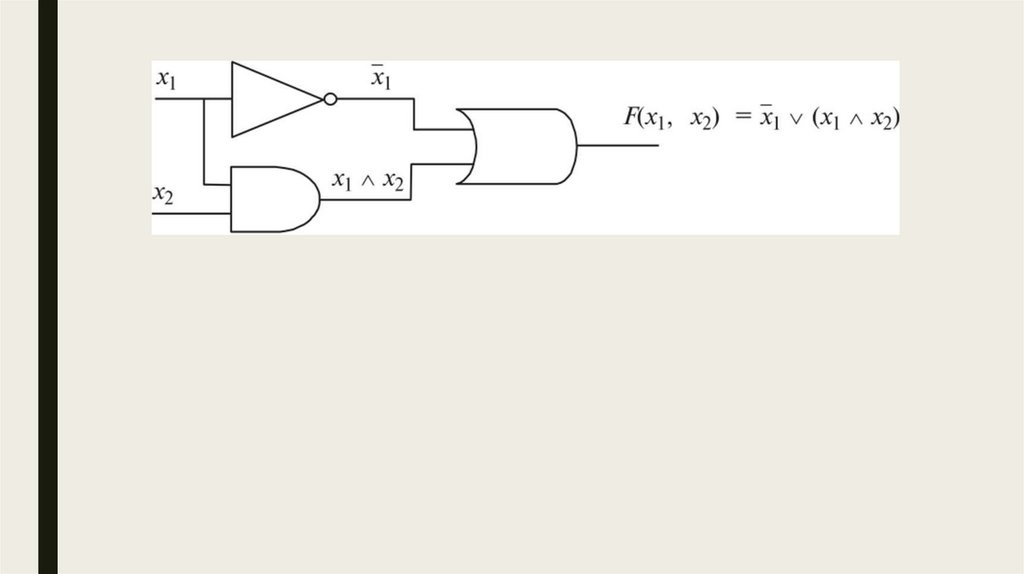
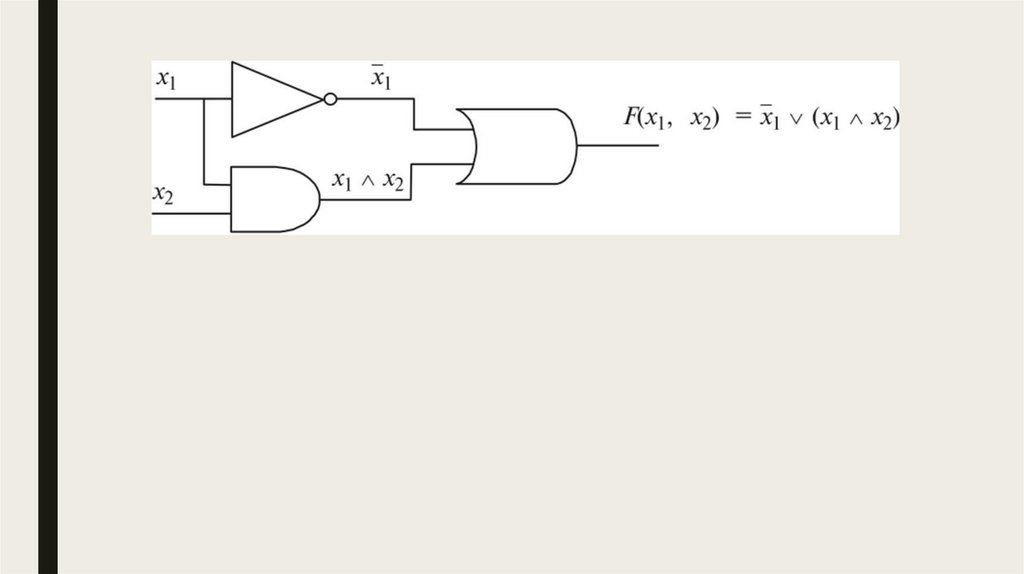
Конъюнкция XY, X•Y, X Л Y, X & Y
Конъюнкцией двух высказываний X и Y называется высказывание,
истинное тогда и только тогда, когда истинны оба высказывания.
Дизъюнкция X v Y
Конъюнкцией двух высказываний X и Y называется высказывание,
истинное тогда и только тогда, когда истинны оба высказывания.

4.

Отрицание ¬X, X
Отрицанием высказывания X называется высказывание, истинное
тогда и только тогда, когда высказывание X ложно.
Импликация X → Y
Импликацией двух высказываний X и Y называется высказывание,
ложное тогда и только тогда, когда X истинно, а Y ложно.

5.

Эквивалентность X~Y, X↔Y, X≡Y
Эквивалентностью двух высказываний X и Y называется
высказывание, истинное тогда и только тогда, когда истинностные
значения X и Y совпадают
Исключающее или X⊕Y
Результат этой операции — истина в том и только в том случае, когда два значения не
равны

6.

При составлении таблицы истинности для логического выражения
необходимо учитывать порядок выполнения логических операций, а
именно:
1. действия в скобках,
2. инверсия (отрицание),
3. & (конъюнкция),
4. v (дизъюнкция),
5. => (импликация),
6. <=> (эквивалентность).

7.

Алгоритм составления таблицы истинности:
■
1. Выяснить количество строк в таблице (вычисляется как 2n,
где n – количество переменных + строка заголовков столбцов).
■
2. Выяснить количество столбцов (вычисляется как количество
переменных + количество логических операций).
■
3. Установить последовательность выполнения логических
операций.
■
4. Построить таблицу, указывая названия столбцов и возможные
наборы значений исходных логических переменных.
■
5. Заполнить таблицу истинности по столбцам.
■
6. Записать ответ.

8.

■ Для приведения логических выражений к эквивалентным, но более
простым в записи используют ряд логических законов

9.

■ Для операций импликации, эквивалентности и исключающего или
нет логических законов. Однако для решения многих задач эти
операции необходимы. Существуют правила замены данных
операций на последовательности операций отрицания, дизъюнкции
и конъюнкции.
■ x → y = ¬x v y
■ x ~ y = (¬x v y)(x v ¬y)
x ~ y = ¬x¬y v xy
■ x ⊕ y = (x v y)(¬x v ¬y)
x ⊕ y = x¬y v ¬xy

10.

■ Табличный способ определения истинности сложного выражения
имеет ограниченное применение. Тогда может быть использован
способ приведения формул к нормальной форме.
■ Аналитическое выражение функции (или формула) находится в
нормальной форме, если в ней отсутствуют знаки эквивалентности,
импликации, двойного отрицания, а знаки отрицания находятся
только при переменных.

11.

■ Простая конъюнкция — это конъюнкция некоторого конечного набора
переменных, или их отрицаний, причём каждая переменная встречается не
более одного раза.
■ Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или
их отрицаний, причём каждая переменная входит в неё не более одного раза.
■ ДНФ – это дизъюнкция элементарных конъюнкций.
■ КНФ – это конъюнкция элементарных дизъюнкций.
■ ДНФ (КНФ) называется совершенной, если каждая переменная формулы входит
в каждую элементарную конъюнкцию (дизъюнкцию) ровно один раз.
■ Полином Жегалкина— это форма представления логической функции в виде
полинома с коэффициентами вида 0 и 1, в котором в качестве произведения
используется операция конъюнкции, а в качестве сложения — исключающее
ИЛИ.

12.

■ Булевы функции с операциями умножения и сложения по модулю 2 образуют
алгебру Жегалкина.
■ Аксиомы алгебры Жегалкина:
■ Операции с константами: A•1 ≡ A;
■ Идемпотентность: A•A ≡ A;
A•0 ≡ 0;
A ⊕ 0 ≡ A.
A ⊕ A ≡ 0.
■ Коммутативность: A•B ≡ B•A;
A ⊕ B ≡ B ⊕ A.
■ Ассоциативность: (A ⊕ B) ⊕ C ≡ A ⊕ (B ⊕ C);(A•B) •C ≡ A• (B•C).
■ Дистрибутивность: A• (B ⊕ C) ≡ A•B ⊕ A•C.
■ Можно перейти от алгебры Буля к алгебре Жегалкина, используя следующие
соотношения: A ⊕ 1 ≡ ¬A;
A v B ≡ A ⊕ B ⊕ A•B.
■ И наоборот, от алгебры Жегалкина к алгебре Буля: A ⊕ B ≡ ¬A•B v A•¬B
■ Перейти к выражению булевой алгебры: (x ⊕ 1)y ⊕ (x ⊕ 1) ≡¬x•y ⊕¬x ≡
¬xy•¬x v x•¬xy ≡ (x v¬y)•¬x v 0 ≡ ¬x¬y.

13.

Функция
Называется двойственной функцией к функции
Если f(0,0,1) = 1; То f*(1,1,0) = 0
■ Если двойственная функция f* совпадает с исходной функцией f, то такая
функция f называется самодвойственной (S).
■ Двойственная к булевой функции может быть получена заменой констант 0 на 1,
1 на 0, дизъюнкции на конъюнкцию, конъюнкции на дизъюнкцию и сохранением
структуры формулы (т.е. соответствующего исходному порядка действий).

14.

■ Функцию f монотонная, если f(α) ≤ f(β) для всех наборов значений
переменных таких, что α ≤ β
■ Множество всех монотонных функций принято обозначать через М
■ Если функция f не является монотонной, то найдутся два таких
набора α, β и индекс i, что
и f(α)=1, f(β)=0, т.е. эти два набора различаются значениями в
точности одной компоненты, а значение функции равно 0 на большем
наборе и равно 1 на меньшем

15.

■ Функция f линейная, если f представима в виде полинома
Жегалкина первой степени, т.е.
■ Множество всех линейных функций обозначают через L
■ Функцию f называют функцией, сохраняющей константу 0, если
f(0,0,…,0) = 0 (T0)
■ Функцию f называют функцией, сохраняющей константу 1, если
f(1,1,…,1) = 1(T1)
■ Множества функций Т0, Т1, S , М , L называются классами Поста

16.

Применение булевых функций к релейноконтактным схемам