Косинус суммы и разности

1.

2.

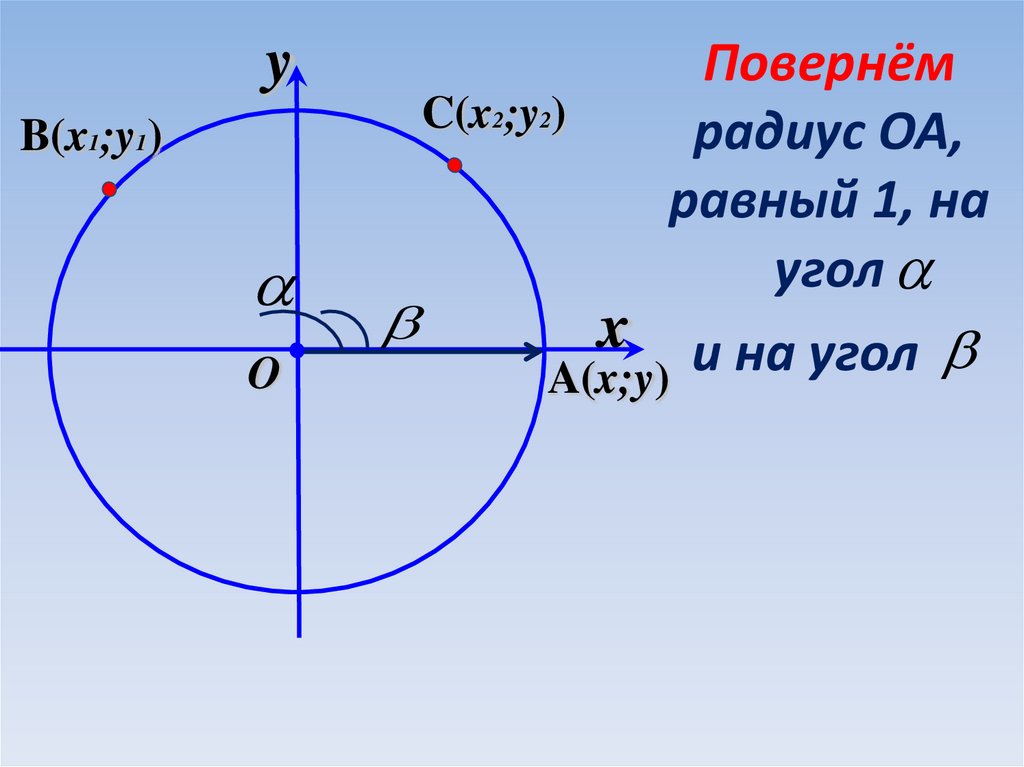
y
Повернём
C(x ;y )
радиус ОА,
равный 1, на
угол
x и на угол
A(x;y)
2
B(x1;y1)
O
2

3.

Найдём скалярное произведение
векторов ОВ и ОС.
C(x2;y2)
y
B(x1;y1)
OB x1 ; y1
x
OC x2 ; y2
O
OB OC x1 x2 y1 y2 (1)
Из определения синуса и косинуса:
x1 R cos
x2 R cos
y1 R sin
y2 R sin
Подставим данные значения в правую часть равенства (1):
OB OC R cos cos R sin sin
2
R 2 (cos cos sin sin )
2

4.

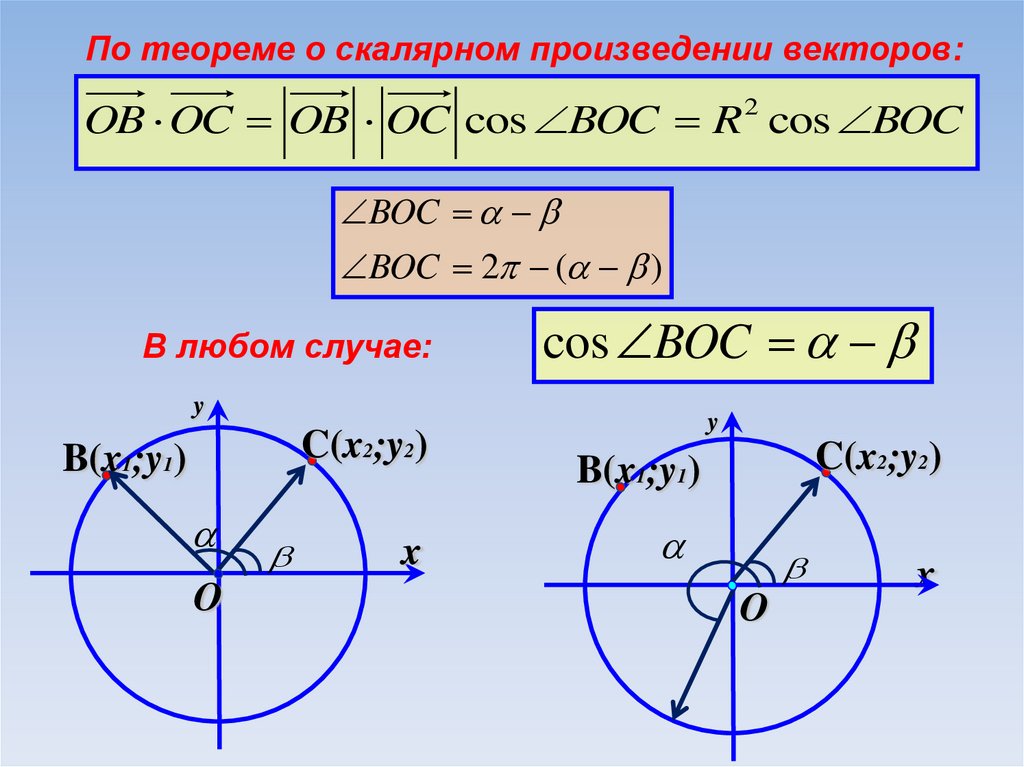
По теореме о скалярном произведении векторов:
OB OC OB OC cos BOC R 2 cos BOC
BOC
BOC 2 ( )
В любом случае:
cos BOC
y
C(x2;y2)
B(x1;y1)
O
x
y
C(x2;y2)
B(x1;y1)
O
x

5.

OB OC R 2 cos( )
OB OC R (cos cos sin sin )
2
Левые части равенств равны, значит правые тоже равны.
Получаем формулу косинуса разности двух аргументов:
cos( ) cos cos sin sin
Формула косинуса суммы двух аргументов:
cos( ) cos( ( )) cos cos( ) sin sin( )
cos( ) cos cos sin sin

6. Закрепление материала

1. Вычислить: 1) cos750
Воспользуемся тем, что 750 = 450 + 300;
cos750 = cos( 450 + 300) =
cos450·cos300 – sin450·sin300=

7. Закрепление материала

1. Вычислить:
2) cos150.
Воспользуемся тем, что 150 = 450 - 300;
cos150 = cos( 450 - 300) =
cos450·cos300 + sin450·sin300=

8. Закрепление материала

2. Вычислить
, если известно, что

9. Закрепление материала

3. Вычислить:
1) cos370cos80 – sin370sin80;
2) cos1070cos170 + sin1070sin170
Ответ: 1)
2) 0

10. Синус суммы и разности двух аргументов

Sin(α+β)= sin α‧cos β+cos α‧sin β
Sin(α-β)= sin α‧cos β-cos α‧sin β